Математические модели рассеивающих диэлектрических объектов

В ряде прикладных задач технической электродинамики, таких как дефектоскопия, радиочастотная томография, радиолокационное подповерхностное зондирование, возникает необходимость строгого анализа электромагнитных полей рассеяния Es,Hs от магнитодиэлектрических объектов при известном поле возбуждения Ei,Hi. Эти объекты могут представлять собой многослойные структуры, образованные средами с различными электрофизическими свойствами (абсолютной диэлектрической и магнитной проницаемостью е, ^, удельной проводимостью ст), структуры, образованные несколькими объектами с различными параметрами е, ^, ст, расположенные в однородной или неоднородной среде, многослойной среде. В большинстве практических задач такие объекты можно считать диэлектрическими, то есть не обладающими магнитными свойствами. Это означает, что ^ = ^о, где ^о -абсолютная магнитная проницаемость вакуума. Исключение составляют среды, где ^ определяется в виде тензора магнитной проницаемости, например, для намагниченных ферритовых сред. Для известного зондирующего поля Ei, Hi измеряемые поля рассеяния от таких диэлектрических объектов несут информацию о внутренней структуре объекта, так как формулировка соответствующей краевой задачи для рассматриваемого объекта включает в себя задание функций е (x, y, z), ст (x, y, z) в каждой внутренней точке, то есть локализацию внутренних неоднородностей объекта. Функции е, ст во внутренней области могут быть гладкими, или кусочно-гладкими (многослойные объекты или совокупность однородных объектов в многослойной среде). Например, в задачах дефектоскопии и радиочастотной томографии задается некоторое эталонное поле рассеяния, соответствующее в пределах определенного допуска известным функциям е, ст. Тогда сравнение эталонного и измеренного поля рассеяния определяет степень их соответствия друг другу. Значительно более сложными являются обратные электродинамические задачи, когда по известному полю рассеяния необходимо определить функции е (x, y, z), ст (x, y, z). Для анализа таких задач необходимо привлечение сложного математического аппарата решения некорректных задач [1].

1.    Постановка задачи

В качестве основного объекта исследования определим функционал поля рассеяния от сложных диэлектрических объектов, при этом будем считать известными функции е, ст . Для построения математических моделей (ММ) задач определения поля рассеяния будем использовать компактные операторные уравнения, основанные на строгих электродинамических соотношениях. Разработка универсального метода формулировки ММ позволит рассматривать определение поля рассеяния от сложных диэлектрических объектов с единых позиций, отвечающих как фундаментальным граничным условиям, так и численному исследованию ММ с заданными требованиями к устойчивости и точности вычислений. Очень близки по постановке к рассматриваемой задаче методы синтеза функций е, ст , обеспечивающих минимизацию поля рассеяния E ^s , НН ^s в заданных угловых областях при известном поле возбуждения E ⁱ , H ⁱ . В частности, использование слоев метаматериалов на идеально проводящем объекте позволяет значительно снизить эффективную площадь рассеяния объекта в широком секторе углов [2].

Рассмотрим область V , заполненную однородным диэлектриком с параметрами Е 2 ,р о , k ₂ = ш ^ е ₂ ц о - волновое число электромагнитного поля в области V , ш - циклическая частота электромагнитного поля, S - поверхность области V . Введем параметры внешней среды е 1 ,р о , волновое число электромагнитного поля этой среде к 1 = ш ^ е 1 р о . С использованием электродинамических соотношений Стреттона-Чу система интегральных уравнений (ИУ)

для сти

эквивалентных электрических и магнитных поверхностных токов J _s , K s на поверхно- S записывается следующим образом [3]:

—*

где

n х E (p) =

— — 4п

i

— div J s grad,

ШЕ n х Нi (p) =

х j ^iajpoJs (Ф1 + Ф 2 ) + 7? s х grad q (ф 1 + Ф 2 ) —

-4 (^Ф1 ⁺ Е 2 ^ф2^) } ^ds 4 ;

1 -— — 4п

—— divK s grad q ( Ф 1 + Ф 2 ) I dS q , шро           ⁴          J

—— —*

х У ^ШЕ1.К s ф ф 1 + Е 2 Ф2^ — J s х grad q (ф 1 + Ф 2 ) —

S1

J s ( q ) = n х Н ; K s (q) =

— n х E ; n - вектор нормали, внешней к V ; p,q G S - точ-

ки наблюдения и источников, соответственно; Ф 1,2 = exp ( — ik i,2 r _pq ) / r _pq ; r _pq - расстояние между точками p, q. Будем считать, что поверхность S удовлетворяет условию Ляпунова [4]: в любых точках p, q G S существуют нормали n _p , n ₄ , непрерывные по Гельдеру - для произвольных чисел с, 0 < а <  1 выполняется условие

системы линейных алгебраических элементов (СЛАУ), к которой редуцируется система ИУ. Например, для диэлектрического цилиндра, основание которого круг радиусом 4А ( А — длина волны электромагнитного поля), высота 10А , типовой объемный конечный элемент для достижения приемлемой точности численного решения имеет объем порядка 0, 3 • 10 ^{- 3} А ³ . Тогда СЛАУ имеет размерность ~ 180000 , решение которой возможно только итерационными методами с использованием суперкомпьютеров. В связи с этим важное практическое значение приобретают подходы, позволяющие снизить размерность рассматриваемой задачи до практически реализуемых значений. В работах [5, 6] показано, что решение 3D задачи для цилиндрических объектов (сечение объекта в плоскости, перпендикулярной оси протяженного объекта, практически неизменно по его длине), асимптотически соответствует решению 2D задачи для бесконечного цилиндра, сечение которого в плоскости, перпендикулярной оси цилиндра, совпадает с аналогичным сечением для 3D задачи. Ограничение – такое соответствие справедливо только для E -поляризации возбуждающего электромагнитного поля. В качестве решения этих задач используется одна и та же функция – электромагнитное поле в дальней зоне в плоскости, перпендикулярной оси объектов. Использование такого подхода позволяет существенно снизить размерность задачи, в частности, для рассматриваемого объекта размерность СЛАУ ~ 8600 . Отметим, что основные технические реализации методов интроскопии основаны на последовательном сканировании поля рассеяния для заданного набора плоскостей измерений. Следовательно, использование соответствия 3D и 2D электродинамических задач позволяет существенно расширить возможности математического моделирования задач рассеяния электромагнитных полей.

2.    Математические модели однородных цилиндрических объектов

Общий подход к решению краевых задач для сред с плоскостной симметрией (существует направление в пространстве, вдоль которого характеристики среды не меняются, все поверхности разрыва – цилиндрические бесконечно-протяженные поверхности с параллельными образующими) заключается в скаляризации исходной электродинамической задачи уже на этапе ее постановки. Рассмотрим бесконечный однородный диэлектрический цилиндр, ось которого совпадает с осью z. Цилиндр расположен в однородной бесконечной области D 1 , которая характеризуется постоянными параметрами £ 1 ,0 1 . Обозначим через D 2 поперечное сечение цилиндра, будем считать, что D 2 представляет собой однородную диэлектрическую среду с постоянными параметрами £ 2 , 0 2 Внешнее возбуждающее поле в области D 1 E -поляризовано, следовательно [7]:

E i = {0,0, u i (x, y)} ; й ■ = { — -L • '/•, • a i(E«l.₀\ . (3)

I wp o dy ШЦ 0 dx J

Краевая задача состоит в определении полей E 1 = E i + E s , Й 1 = Й i + Й s в области D 1 , E 2 , Й 2 в области D 2 , удовлетворяющих уравнениям Максвелла, граничным условиям, обеспечивающим непрерывность тангенциальных компонент E 1 , Й 1 и E 2 , Й 2 на контуре L 1 , ограничивающем область D 2 . Кроме того, поле рассеяния E ⁸ ,й s должно удовлетворять условию излучения на бесконечности Зоммерфельда–Реллиха.

Будем считать, что контур L 1 удовлетворяет требованию непрерывности нормали (2). Введем в рассмотрение две функции Грина G 1,2 ( p, q ) , для каждой из которых справедливо условие излучения и соответствующее однородное уравнение Гельмгольца:

△ G 1,2 ^{( p} , ^{q )} + ^k l,2 G 1,2 ^{( p} , ^{q )} = ^— ^ ^{( p — q )} ,

где А = д ² /дх ² + д ² /ду ² + д ² [dz ² - оператор Лапласа; 5 (p — q) - дельта-функция. Функции Грина имеют следующий вид [4]:

G 1,2 ⁽ p, q) = ^— ^H Q ² ) ^{( k} i,2 r pq ) ,

где H 02 ( k i,2 r pq ) — функция Ганкеля второго рода нулевого порядка. С использованием второй формулы Грина и граничных условий на L i запишем следующую систему ИУ [7]:

u i

(p) = u2

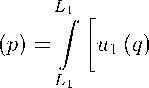
д

∂n _p ∂n _q

∂ ui (q) д— (Gi — G2) — U2 (q) (Gi — G2) ∂nq

dl q + u i ( p ) ; p, q G L i ;

^{( G} i ^— G 2 ) ^{— u} 2 ⁽ q) дП” ^{( G} i ^{— G} 2)]

dl q ⁺ an; ^u i ^{( p )}

где u i = E zS - скалярная компонента поля рассеяния; U 2 = дu i /дп ; n - вектор нормали, внешней к области D 2 . Введем следующие обозначения: д/дn _q = д _ц ; д/дп _; = д _; ; д ² /дп _; дп _ц = д²_ч ; g _i2 (p, q) = G i (p, q) — G ₂ (p, q) . Кроме того, введем матрицы-столбцы u = [ u _i u ₂ ] t , u i = [ u i д _p u ⁱ ] t , t - символ транспонирования. Для компактной записи системы ИУ (6) введем функциональный матричный оператор (ФМО):

,(j) = / Г ^д 9 g ml ml J L ^ди g ml

L j

- g _ml

- ∂ p g _ml

]

dl q , p, q ∈ L j ,

заданный на контуре L j – границе раздела сред ( B – boundary), внешняя среда определяется функцией Грина G m (p, q) , внутренняя среда - G i (p, q) . Строго говоря, оператор B mm) не является интегральным, так как в общем случае области определения функций и отображений могут не совпадать. Тогда систему (6) можно записать в операторной форме:

u = B 12) u + u i -

Так как (8) – система ИУ Фредгольма II рода, то ее решение существует и является единственным в классе функций с непрерывной в смысле Гельдера производной. Отметим, что операторное уравнение (8) позволяет построить итерационный метод решения по следующей схеме:

u ^{( m}+ ⁱ ) = в (2) u ^{( m )} + u i , m = 0,1, 2,...                               (9)

Такой метод может быть использован для задач большой размерности. Итерационные методы позволяют контролировать скорость сходимости решения с возможностью адаптивного управления критерием точности решения (правило останова).

Решение уравнения (8) определяет основной объект исследования – функционал поля рассеяния в произвольной точке внешней среды D :

E z^s (p) =

L 1

[u i (q) д _р G i — u 2 (q) G i ] dl q ,

p G D ; q G L .

Введем ФМО следующего вида:

P Ij) = / [

L j

д q G i

^{— G} i ] ^dl q ,

отображающий решение уравнения (8) на контуре L j в заданное множество точек ( P – point) в области D 1 . Тогда функционал (10) можно записать в компактной форме:

E s (p)= P ^j u, p G S i .                               (12)

Для вычислительных экспериментов использовалась система MATLAB, поэтому в дальнейшем будем придерживаться обозначений, характерных для этой системы.

Рассмотрим основные особенности операторного уравнения (8), которое является базовой ММ для более сложных диэлектрических объектов.

• 1.    Этап численного исследования ММ рассматриваемой задачи в виде уравнения (8) предполагает рациональную дискретизацию контура L1 для перехода к блочной матрице Bh = [bl 1 bi2; b2i b22] , где блоки bmn представляют собой векторы-строки коэффициентов, образованных применением квадратурных формул к ядрам ИУ. Для сложных диэлектрических объектов большое значение приобретают вопросы унификации программного обеспечения ММ, предполагающие единый подход и однотипные численные методы для программирования отдельных блоков уравнения (8). В этом случае погрешности численного исследования отдельных блоков имеют общий порядок, что позволяет прогнозировать точность моделирования для всего объекта. В частности, вычислительные эксперименты показали высокую эффективность квадратурных формул Гаусса–Лежандра, когда для достаточно гладких контуров диэлектрических областей можно получить приемлемую точность вычислений уже для 5. . . 7 внутренних узлов. Дискретная форма операторного уравнения (8) в виде СЛАУ выглядит следующим образом:

• 2.    Известные координаты узлов дискретизации (xi,yi), i = 1,n, позволяют определить коэффициенты любого блока матрицы B_h с помощью собственной матрицы взаимных расстояний rpq = {rpq}_nxn, rpq = aJ(x_p — xq)²+ (y_p — yq)2. Так как основное время заполнения матрицы Bh занимает вычисление функций Ганкеля и их производных, то рациональная организация численных процедур и формирования матрицы B_h из блоков приобретает большое практическое значение. Использование эффективного метода вычислений цилиндрических функций в системе MATLAB именно для матричных аргументов позволяет значительно уменьшить время моделирования, а использование переадресации внутри блочных элементов с помощью неявных циклов вида m = 1 : n удобно для формирования общей матрицы Bh .

• 3.    В случае совпадения точек p и q ядра ИУ имеют интегрируемую логарифмическую особенность [7]. Подробное выделение особенности для узла, находящегося в интервале дискретизации Alm, основано на аналитическом и численном интегрировании и может быть получено с высокой точностью. Эти результаты могут быть введены во все остальные интервалы практически без изменения, так как формальная дискретизация контуров обычно предусматривает однородность интервалов Alm. Кроме того, доминирующая главная диагональ СЛАУ сглаживает небольшие погрешности процедуры выделения особенности при некоторой неоднородности Al_m . Такой прием ускоряет время заполнения матрицы B_h без заметного изменения точности моделирования, что подтверждено вычислительными экспериментами.

3.    Математические модели многослойных диэлектрических объектов

A h u h = u h ,                                       (13)

где A h = E — B h ; E - единичная матрица; A h = { a _mn } 2_nx2n ; n — число узлов дискретизации контура; U h = { u _m } _{2 nx 1} — решение уравнения (8) в узлах дискретизации; u h = {um} _{2 nx 1} - известный вектор возбуждающего поля в узлах дискретизации контура. Особенностью СЛАУ (13) является доминирующая главная диагональ, обеспечивающая высокую устойчивость решения и слабую зависимость от влияния погрешностей, вызванных дискретизацией контура.

Оценка точности ММ может быть произведена сравнением с известными решениями, например, полученными аналитически. Известно строгое решение однородного уравнения Гельмгольца для поля рассеяния плоской волны на однородном круговом диэлектрическом цилиндре в виде бесконечного ряда по цилиндрическим функциям Бесселя–Ганкеля [8]. Такая форма представления решения удобна для оценки точности численной реализации тестового решения, когда ограничение суммируемых членов ряда производится по заранее выбранному критерию. Следует особо отметить, что в ряде случаев сходимость рядов по цилиндрическим функциям может оказаться очень медленной, тогда как численное исследование ММ свободно от этого недостатка. Вычислительные эксперименты для широкого интервала значений £ 2 ,^ 2 показали, что даже для относительно больших интервалов дискретизации контура ( ~ А/10 ), относительная погрешность моделирования не превышает величин 10 - ² , при этом время вычислений аналитического решения и время численного решения операторного уравнения (8) практически совпадают. В качестве примера на рис. 1 приведены результаты исследования поля рассеяния плоской волны на круговом диэлектрическом цилиндре: диаметр цилиндра d = ЗА ; относительная диэлектрическая проницаемость области цилиндра E r2 = 3,1 — 0, 045i ; сплошная линия - численное решение ИУ, точки -аналитическое решение в виде бесконечного ряда по функциям Бесселя–Ганкеля. Для удобства сравнения решений использован логарифмический масштаб оси ординат. Сравнение показывает хорошее соответствие результатов численного исследования ММ диэлектрического объекта и известного аналитического решения (для интервала дискретизации контура Al = 0, 092А относительная погрешность вычислений не превышает 0,011).

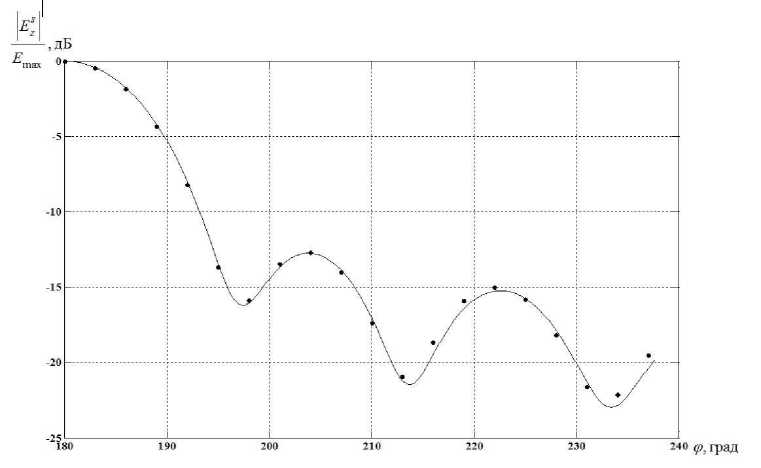
Рис. 1 . Нормированное распределение амплитуды поля рассеяния

Общий вид двумерных многослойных диэлектрических объектов представлен на рис. 2.

Каждый контур L m является границей раздела сред D m , D m+i с параметрами E m , a m и E m+1 , a m+i . Для контура L m , ( m = 1, m = N, N >  2) аналогично (6) запишем следующую систему ИУ:

^U m,1

И

L m +1

^U m,2 —

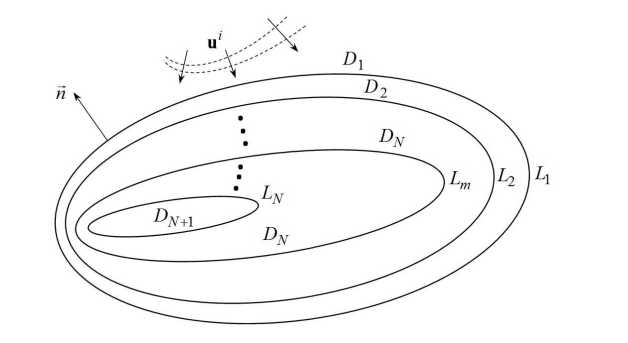
Рис. 2 . Двумерный многослойный диэлектрический объект

j [ ^U m-1,1 ^d q G m

L m -1

-

^U m-1,2 ^G m ] dl q + j [ ^U m,1 ^d q g m,m+1 L m

,1 ^d q G m+1 ^U m+1,2 G m+1 ^] dl q ;

j [U m-1,1 d pq G m L m - 1

—

U m-1,2 d p G m ] dl q +

U m,2 g m,

dl q +

+ j [ ^U m,1 ^d pq g m,m+1

-

^U m,2 ^d p g m,m+1] dl q +

L _m

+ j [ ^U m+1,1 ^d pq ^G m+1

-

u m+1,2 ^d p ^G m+1 ] dlq , ^{p E} L m , ^m — 2, N 1.

L m +1

Если m — 1 , то первое слагаемое первого уравнения системы (14) необходимо заменить на u i (p) , первое слагаемое второго уравнения на d p U i (p) . Если m — N , то в уравнениях системы (14) необходимо исключить третьи слагаемые. Введем ФМО следующего вида:

I (j ) _— / mk

L j

∂qGm pq m

^^^^^^^^^»

—

G m

∂ p G m

dl q , p E L k ^; ^П ^{— -} [

L i

∂ q G l

. d p ² q G 1

- G l

- ∂ p G l

dl q , p ∈ L n , (15)

где оператор I mk ( I - inside ) отображает решение на контуре L j внутрь среды D m на контур L k ; оператор О^ ( O - outside ) отображает решение на контуре L i во внешнюю среду на контур L n . Тогда система ИУ (15) принимает следующий вид:

^u m — I m, _m ^^um-1 + B m,m+1 ^u m ⁺ O m,m+1 ^U m+1 , ^u m — ^[u m,1 ^u m,2 ^] , ^m — 2, N 1, ⁽¹⁶⁾

то есть решение на каждом внутреннем контуре непосредственно связано с решениями на двух соседних контурах, за исключением первого и последнего контура. Объединяя все системы вида (16) в одно операторное уравнение, получим:

U — B 1,N U + U i ,

где B i ,n — трехдиагональный ФМО следующего вида:

В ⁽¹⁾ B 12

I^W I 22

О ⁽²⁾ O 21 м ⁽²⁾ B 23

О(3) O32

B 1,N —	T (m- 1 ) I mm	(1) B m,m+1	C) ( m +1) O m+1,m
	..	.	.   .   .. T (N-2)      „(N-1)   ^(N) I N -1,N-1 B N -1,N O N,N -1 T (N-1)    r(N ) I N,N     B N,N +1 J

u = [u 1,1 U 2,1 U 1,2 u ₂ , ₂ -u m,1 u m, ₂ •••u ₁ ,N u ₂ ,N ] t ; u i = [u i d p u i 0 0... 0 0... 0 0] t . Компактная форма представления оператора B 1,N в виде ленточной матрицы { b } _{Nх 3} позволяет формализовать процедуру построения ММ многослойного диэлектрического объекта с учетом блочной структуры операторов I j , B ^j^ , O m _n , каждый из которых определяется независимо. Кроме того, вид ФМО приводит и к ленточной матрице СЛАУ, при этом большое количество нулевых коэффициентов разреженной матрицы предполагает компактную форму ее хранения и обработки в оперативной памяти.

4.    Примеры формализованного построения ММ сложных диэлектрических объектов

Пример 1. Рассмотрим формализованную процедуру построения ММ объекта, состоящего из N вложенных однородных диэлектрических областей с различными параметрами, расположенных в однородной замкнутой области D 1 (рис. 3):

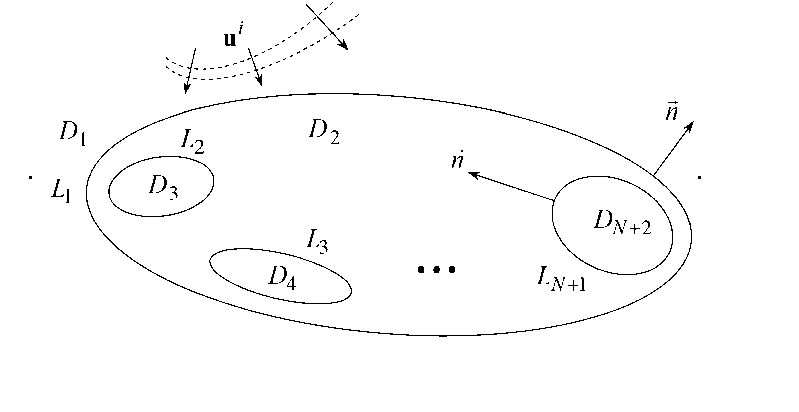
Рис. 3 . Двумерный диэлектрический объект: вложенные области

Система операторных уравнений для каждого контура выглядит следующим образом:

N +1

• u 1 — B 12 u 1 + \ о 21) u n + u i , p ^Е L 1 ;

n=2

N +1

• — T ^{(1)         ( m )}        \ ^{Л   ( n )}         i m            1 C /

u m — I2m ^u 1 ^{+ B} 2m u m ⁺ _v O2 m u ^{n +} u , m — 2, N + 1; p t ^L m .

n=m

Объединяя систему уравнений (19), получим формулировку ММ рассматриваемого объекта в виде обобщенного операторного уравнения:

u = B 1,N+1 u + u i ,

где ФМО имеет следующий вид:

	в (1) B 12 I (1) I 22	о 22      . в (2) B 22      .	(m) O 21 (m) O 22	П (N+1) 1 . O 21 П (N+1) . O 22
B 1,N +1 =	. I (1) I 2 m	.. о (2) 2m     .	. (m) B 2 m	.. П (N+1) . O 2 m	,                      (21)
	. I (1) I 2,N +1	.. (2) O 2,N +1   .	. (m) O 2,N +1	.. R (N +1) . B 2,N +1

Пользуясь полученными результатами, сформулируем общие принципы формализованного построения ММ сложных диэлектрических объектов.

• 1.    Вводится система обозначений областей и соответствующих им контуров диэлектрического объекта. Индексацию областей и контуров удобно начинать с внешней, неограниченной среды D 1 , в которой определяется поле рассеяния. Тогда внешний контур (или контуры) обозначается как L 1 (или L 1 , L ₂ , L 3 ... ). Дальнейшая индексация производится по мере перемещения внутрь объекта.

• 2.    Строка с номером m ФМО размерностью N х N , где N - общее количество контуров объекта, определяет решение на контуре L _m . В этой строке на пересечении со столбцом m всегда располагается блочный оператор B nm ) , где n, l - индексы внешней и внутренней сред, разделенных контуром L _m .

• 3.    Для контура L _m определяются все контуры, расположенные в той же среде D _n , что и контур L _m . Все эти контуры определяют блочные операторы O ni) , где i - индексы контуров. Эти блочные операторы располагаются на пересечении строки m с столбцами i .

• 4.    Если среда D _n ограничена контуром L _u , то на этом контуре задается блочный оператор I nm , который располагается на пересечении строки m и столбца и. В строке m может располагаться только один блочный оператор I nm .

• 5.    Для среды D l , ограниченной контуром L m , определяются все внутренние контуры, для каждого из которых задается блочный оператор O j) , который располагается на пересечении со столбцом j .

• 6.    Для возбуждающего поля, заданного во внешней среде D 1 , правая часть операторного уравнения всегда унифицирована: u i = [u i д _р и^г 0 0 ... 0 0 ... 0 0] t .

• 7.    Решение операторного уравнения u определяет поле рассеяния во внешней среде в соответствии с выражением (12).

Следуя указанной процедуре, можно построить ММ сложного диэлектрического объекта, составленного из отдельных однородных диэлектрических объектов. На практике, даже в случае отсутствия четко выраженных границ однородных областей, всегда можно выделить подобласти, в которых параметры среды можно считать практически постоянными. Вычислительные эксперименты показывают, что исследование ММ в виде предложенных ФМО предпочтительнее решения ИУ для неоднородных сред, для которых вводятся функции е ( x,y,z) ,а ( x,y,z).

Пример 2. Рассмотрим прямую формализованную процедуру построения ММ диэлектрического объекта, не прибегая к выводу системы операторных уравнений. Объект состоит из вложенных многослойных однородных диэлектрических областей с различными параметрами, расположенных в однородной замкнутой области D1 (рис. 4).

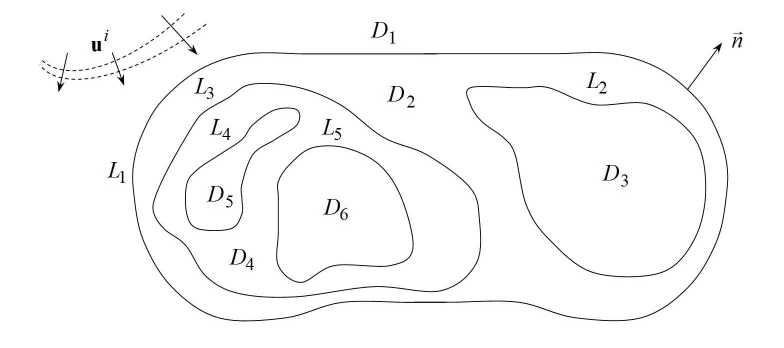
Рис. 4 . Двумерный диэлектрический объект: вложенные многослойные области

ФМО для выбранной системы обозначений выглядит следующим образом:

(1) B11 (2) O21 (3) O21 . . I(1) I 22 (2) B23 (3) O22 . . B1,5 = I(1) I 23 (2) O23 (3) B24 (4) O43 (5) O43 ,                             (22) . . (3) I44 (4) B45 (5) O44 . . (3) I45 (4) O45 (5) B46 J общее операторное уравнение с этим ФМО для ММ объекта:

u = B 1,5 u + u i ,                                       (23)

где u = [u i u ₂ и з u ₄ u ₅ ] t ; u i = [u i d p u i 0 0 0] t .

Выводы

• 1.    Блочная структура ФМО позволяет формировать матрицу СЛАУ в виде независимых блочных матриц с использованием унифицированных программных комплексов, ориенти-

• рованных на получение погрешностей дискретизации одного и того же порядка.

• 2.    Использованием формализованного принципа построения ФМО позволяет исследо-

• вать ММ сложных диэлектрических объектов с использование универсального операторно-
• го уравнения, блочные операторы которого представляют собой матричные операторы вида

• 3.    Использование квадратурных формул Гаусса–Лежандра повышенной точности позволяет исследовать ММ сложных диэлектрических объектов без проведения процедур выделения особенностей ИУ, которые дают только асимптотические оценки поведения ядра ИУ. Прямое вычисление коэффициентов СЛАУ с использованием эффективных программ

• 4.    Рациональная организация формирования блочной структуры СЛАУ, к которым редуцируются ИУ, существенно ускоряет процесс заполнения матриц ММ. Это расширяет возможности математического моделирования сложных диэлектрических объектов.

p ⁽ⁿ⁾ r( ⁿ) ^{( n ) B} ml ^{, I} ml ^{, O} ml ^.

численного интегрирования дает возможность получения оценок погрешностей для однородного характера вычислительных процедур. При этом отмечается заметное уменьшение времени вычислений, что представляет практический интерес при проведении очень большого количества циклических расчетов ДН, особенно при решении СЛАУ высоких порядков, проведении оптимизации поля рассеяния.