Математические модели сфероидальных спирально-рамочных излучателей
Автор: Табаков Д.П., Валиуллин Р.М.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.26, 2023 года.
Бесплатный доступ
В статье рассмотрены математические модели двух сфероидальных спирально-рамочных излучателей, построенные на основе общего подхода, предполагающего использование интегрального представления электромагнитного поля. Построение моделей осуществлялось в тонкопроволочном приближении. Внутренняя задача электродинамики сведена к системе интегральных уравнений Фредгольма 1-го рода. Решение полученной системы осуществлялось методом моментов с кусочно-постоянными базисными функциями и дельта-функциями в качестве тестовых функций. При этом осуществлялась локальная линеаризация образующих проводников рассматриваемых структур. Проведены исследования зависимостей распределений токов, входного сопротивления и характеристик излучения структур от частоты. Показано, что в рассматриваемых структурах возможно существование стоячих, бегущих и смешанных волн тока. Режим тока определяется волновыми размерами и геометрией структур и определяет характер поведения волнового сопротивления в диапазоне частот. Несмотря на схожую геометрию, характеристики рассмотренных структур имеют определенные отличия.
Спиральные антенны, рамочные антенны, интегральное представление электромагнитного поля, тонкопроволочное приближение, диаграмма направленности, входное сопротивление
Короткий адрес: https://sciup.org/140297874
IDR: 140297874 | УДК: 537.862 | DOI: 10.18469/1810-3189.2023.26.1.38-48
Текст научной статьи Математические модели сфероидальных спирально-рамочных излучателей
Спиральные антенны (СА) на сегодняшний день представляют собой обширный класс излучающих структур, геометрия и характеристики которых соответствуют заранее заданным и довольно разнообразным требованиям. Основными достоинствами СА можно считать возможность достижения широкой полосы рабочих частот, хороших характеристик направленности излучения, возможность электрического управления поляризационными характеристиками излучения, а также разнообразие форм излучающих элементов. При соблюдении принципа углов и принципа взаимодополняемости реализуются частотно-независимые варианты СА, коэффициент перекрытия для которых достигает нескольких десятков единиц [1]. СА применяют в антенной технике в качестве самодостаточных излучающих структур, в качестве облучателей зеркальных антенн, в фазированных антенных решетках, при построении замедляющих систем и в других элементах устройств СВЧ [2].
В текущий момент интерес к спиральным элементам также связан с развитием теории метаматериалов [3], частным случаем которых можно считать киральные структуры [4]. Внедрение проводящих частиц различной конфигурации (в данном случае спиральных частиц) в исходный материал ведет к изменению его электродинами-
ческих свойств. Подобные структуры могут быть использованы в качестве частотно-селективных элементов, в преобразователях поляризации, в качестве малоотражающих покрытий и концентраторов СВЧ-энергии. Естественно, что построение упомянутых выше структур требует наличия математических моделей (ММ) их базовых элементов, в качестве которых в данном случае выступают спиральные элементы, в общем случае описываемые достаточно большим числом параметров. В настоящий момент для исследования киральных структур используют феноменологические уравнения, оперирующие параметром киральности χ [4–6]. Значение и знак данного параметра зависят от длины волны и типа базовых элементов. Определение параметра киральности осуществляется приближенными методами. При этом использование феноменологических уравнений имеет существенные ограничения, связанные с взаимным расположением и волновыми размерами элементов, образующих структуру. В целом для метаматериалов вполне приемлемой считают практику описания на основе эффективных диэлектрической и магнитной проницаемостей, в общем случае имеющих тензорный вид. Для анализа спиральных структур используют как приближенные, так и строгие подходы. В рамках приближенных подходов производится замена исходного излучателя упрощенным эквивалентом (решеткой
LM^^e © Табаков Д.П., Валиуллин Р.М., 2023
кольцевых элементов, одиночным кольцевым элементом, анизотропно-проводящей моделью и т. д. [2; 7]). При этом наиболее адекватными данные подходы можно считать применительно к регулярным спиральным структурам. При исследовании нерегулярных структур используют принцип локальной эквивалентности, дополнительно снижающий соответствие приближенного решения точному решению поставленной задачи.
Проблемой существующих в настоящий момент точных методов, используемых в системах автоматизированного проектирования (CST MWS, FEKO, HFSS), являются высокие требования к вычислительным ресурсам, являющиеся следствием их универсальности, а также численный характер получаемых результатов, которые не всегда можно корректно интерпретировать. Поэтому построение строгих и эффективных с вычислительной точки зрения математических моделей спиральных элементов и структур, использующих эти элементы в своей основе, представляет собой на сегодняшний день актуальную задачу.
Наиболее точными являются ММ, построенные на основе интегральных уравнений (ИУ) различного типа [8–11]. Наибольшее распространение получили ММ в виде систем ИУ Фредгольма первого рода, получаемых с использованием тонкопроволочного приближения [12]. Здесь можно отметить, что полная ММ рассматриваемой структуры должна содержать в себе решение как внешней (определение ЭМП в любой точке пространства), так и внутренней (определение токовых функций из граничных условий на элементах структуры) электродинамической задач. Система ИУ представляет собой решение только внутренней задачи. Поэтому построение ММ целесообразно осуществлять на основе соответствующего интегрального представления ЭМП (ИП ЭМП), сохраняющего непрерывную взаимосвязь между токовыми функциями и порождаемыми этими токовыми функциями ЭМП в любой точке пространства.
В [13] на основе тонкопроволочного ИП ЭМП осуществлено построение ММ цилиндрических спиральных элементов двух типов (обычного и совмещенного). Решена задача дифракции на этих элементах. Показано, что внутренняя структура элемента оказывает существенное влияние на характеристики рассеянного поля. Так, на совмещенном спиральном элементе в достаточно широком диапазоне частот возникает эффект ортогонального рассеяния, когда угол между волновыми векторами первичной и рассеянных электромагнитных волн составляет величину, близкую к 90°.
В [14] рассмотрена эллипсоидальная спиральная частица, ММ которой также построена на основе ТП ИП ЭМП, но при этом проведен подробный анализ решения спектральной задачи, заключающийся в определении поведения собственных функций и собственных чисел интегрального оператора в полосе частот. Показано, что решение внутренней задачи в целом определяется собственными функциями, имеющими наименьшее по модулю значение связанных с ними собственных чисел.
В настоящей статье предлагаются ММ двух типов спирально-рамочных излучателей, для которых в диапазоне частот исследуется численное решение внутренней задачи, а затем определяются характеристики излучения и входное сопротивление. Данные излучатели могут быть использованы в качестве самодостаточных антенн либо в составе более сложных антенных систем.
1. Физические модели и геометрия излучающих структур
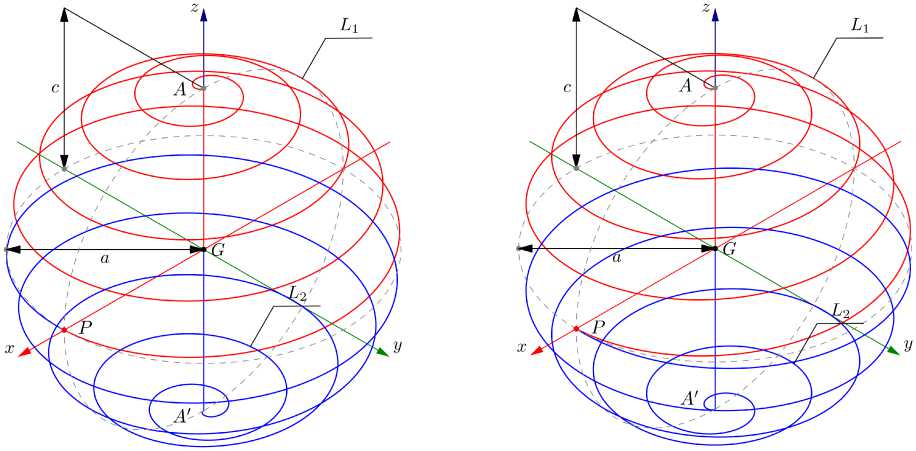
Геометрия излучателей представлена на рис. 1. Обе структуры включают в себя прямолинейный осевой проводник A'A , расположенный вдоль оси Oz , и пару спиральных проводников AP и A ‘ P , соединенных друг с другом в точке P и с соответствующими концами A и A ‘ осевого проводника. Структура, показанная на рис. 1, а , содержит обычную эллипсоидальную спираль (далее эту структуру мы будем называть А-спиралью). Структура на рис. 1, б содержит спираль с изломом: ее нижняя часть является зеркальным отображением верхней части относительно плоскости XOY.
Проводники структуры имеют одинаковый радиус, равный б ^ X , где X - длина волны излучения. В точке G осевой проводник имеет разрыв длиной 2 b ^ X , в который помещен источник стороннего поля (генератор ЭДС). Касательная компонента стороннего поля на проводниках E (in) равна нулю всюду, за исключением области разрыва, в которой она равна U / (2 b ), где U - напряжение генератора ЭДС. Под действием стороннего поля в проводниках возникает распределение электрического тока I ( l ), вид которого необходимо определить при решении внутренней электродинамической задачи. Так как 2 b ^ X , то функция I ( l )
б
a
Рис. 1. Геометрия исследуемых структур: без излома ( а ) и с изломом ( б )
Fig. 1. Geometry of the structures under study: without a break ( a ) and with a break ( b )
является непрерывной в области разрыва. Также при построении ММ будем считать, что проводники имеют бесконечно большую проводимость.
Обобщенное параметрическое уравнение образующей Ls спирали имеет вид
L s : r ( ф ) = a cos( gф )cos ф x + (1)
+ af (ф) cos(gф)sin ф y + c sin( gф)Z, g = 1/(2Nl),фе [-1;1]-nNl.
Здесь a - радиус сфероида, c - его полуось, ф -параметр на образующей (по сути, азимут цилиндрической системы координат), Nl – число витков спирали. Для А-спирали f ( ф ) = 1, для Б-спирали f ( ф ) = sgn( ф ), где sgn( ф ) - функция знака. Для перехода в (1) от параметра ф к естественному параметру l необходимо определить функцию ф = ф ( l ), обратную функции
ф l (ф) = J
8 r ( ф' ) ‘ дф
d ф' ,
и подставить ее в (1). Отметим, что эта задача в данном случае может быть решена только численно методом обратной интерполяции [15]. Уравнение осевого проводника Lv записывается непосредственно в естественном параметре l :
L v : r v ( l ) = l Z , l e [ - c ; c ].
F ( r ) = £ f ( r ; r j , j ; F = E , H , (4)
j где
F ( r ; r , I - )= I ( l ' ) K F ( r , r ( l ' )) dl ' , F = E , H (5)
jj L jaj
– ИП ЭМП от тока Ij ( l ), локализованного на образующей Lj ТПС,
W
KE (r, r (l')) = -^mI l,■ (l'kk2G (r, r (l')) + a j ik ( j a
+ 1^ ( ( r - r j ( l ')) Ba ( r ’ r j ( l ')) ) } ;
K H ( r , r ( l ' )) = ( ( r - r j ( l ' )) X l j ( l ' ) ) B a ( r , r j ( l ')),
– ядра ИП ЭМП; ˆ l j ( l )= d r j ( l )/ dl – касательный орт на образующей Lj , Wm является волновым сопротивлением среды, а k – ее волновым числом;
ikR + 1 exP ( - ikR )
B =-- G , G =----------- ,
R 2 4 П R
G ( R ) – функция Грина, определенная для свободного пространства; R ( r , r ')=| r - r ' | - расстояние между точкой источника и точкой наблюдения;
Fa ( r , r j ( l ')) = F ( Ra ( r , r j ( l '))), F = G , B
– компоненты ядер,
Ra ( r , r j ( l ')) = | r - r j ( l ')|2 +e 2
– расстояние между точкой источника и точкой наблюдения, регуляризированное малым параметром в , роль которого играет радиус проводников. В нашем случае в (4) будет фигурировать пара проводников L 1 = Lv и L 2 = Ls .
Интегральное представление ЭМП (4) содержит токовые функции I j ( l ), подлежащие определению. Это можно сделать, применив граничное условие на поверхности проводников. Учитывая, что б ^ X , граничное условие можно ослабить, перейдя с поверхности проводников на их образующие. В итоге имеем:
l ( r ( l )) ■ ( E ( in ) ( r ( l )) + E ( r ( l )) ) = 0.
Результатом применения представленного ГУ к ИП ЭМП является система ИУ вида
- l ( r i ) ■ E ( in ) ( r i ) = l ( r i ) ■ ^ E ( r ; r jj , I j ); (7)
i , j ^v, N .
Приведенная система ИУ классифицируется как система ИУ Фредгольма 1-го рода [16]. Осуществим дискретизацию (4), заменив образующие ломаными:
{ N }
L j ^ L j : r j ,1 , r j >2 , ^ , r j , N + 1 ,
здесь Nj + 1 – число узлов ломаной; j – индекс проводника. Для каждой ломаной можно определить уравнение ( j , kj ) -сегмента:
r jk = r jk + l jkl , l ∈ [ -∆ j /2; ∆ j /2], (9)
,j,j,j здесь:
*
r j , k , j
l j , k , j
rj,k +1+ rj,k +1 ,j,j rj,k +1- rj,k +1 ,j,j
∆ j
∆ j =| r j , k + 1 - r j , k + 1| , j , j
–
комплексная ампли-
туда тока ( j , k j ) -сегмента. Тогда для дискретизированных образующих на основе (4) получаем ИП ЭМП совокупности N излучателей, имеющих сегментированные образующие:
N Nj ∆ j /2
F ( r )= ЕЕ I j , k. J K F ( r , r , k. ( l ‘ ))dl ‘ , F 5 E , H . (11) j =1 kj =1 j -∆ j /2 j
Использование (11) предполагает знание неизвестных амплитуд токов Ij k . В рамках выбран-,j ного метода решения системы ИУ необходимо потребовать выполнения граничного условия типа (6) в центрах сегментов. В результате имеем СЛАУ вида
N Nj ∆ j /2
-i»E(in’(r) = ЕЕjk. J ii,k. ■ KE(r.ri.k.(l‘))d‘, (12)
3. Результаты численного моделирования
i j=1kj=1 j-∆j/2 i j i = 1,., N, kj = 1,., N.
При соблюдении условия
2 ε≤∆ j ≤ 12 ε (13) для всех j достигается устойчивое решение СЛАУ [12]. Достоверность результатов, получаемых на основе (11) и (12), подтверждается в работе [17].
При численном моделировании исследовались А- и Б-спирали, геометрия которых определялась следующими параметрами a / c =1/4,1/2,3/4 и 1; число сегментов спирального элемента в указанных случаях было равно 200, 400, 600 и 800 соответственно, число сегментов осевого проводника составляло 80 для всех a / с . Число витков спирального элемента было равно пяти, отношение радиуса проводника ε к полуоси c было равно б / с = 3/1000. Указанный выбор геометрических параметров удовлетворяет условию (13), выполнение которого обеспечивает корректное решение внутренней задачи. В качестве главного параметра, нормируемого к длине волны X , была выбрана удвоенная полуось c структур, определяющая их высоту.
На рис. 2 представлены результаты расчета амплитудных распределений тока на проводнике AP обеих структур для различных соотношений 2 с / X при a / с = 1/2. Значение 2 с / X указано непосредственно на рисунках. Из рисунка видно, что при 2 с / X < 0,5 в спиральных проводниках устанавливается режим стоячей волны тока, а сами распределения для А- и Б-спиралей имеют довольно мало отличий. Возникновение данного режима связано с тем, что потери на излучение при расстояниях, соизмеримых с длиной волны, довольно малы, в результате чего в спиральном проводнике имеется пара встречно распространяющихся бегущих волн с практически не меняющейся амплитудой. Их сумма представляет собой стоячую волну, которую мы можем наблюдать на данном рисунке при 2 с / X = 0, 05 0,25, 0,5. При 2 с / X = 0,6 в спирали устанавливается режим смешанной волны тока, наибольшую разность амплитуд на спирали встречно бегущие волны имеют вблизи точек A и A ‘ , а наименьшую - в точке P . Поэтому в окрестности точки P сохраняется режим стоячих волн тока. Вполне справедливым будет утверждение о том, что для указанного соотношения 2 с / X = 0,6 бегущие и стоячие волны тока вносят соизмеримый вклад в общее поле, создава-
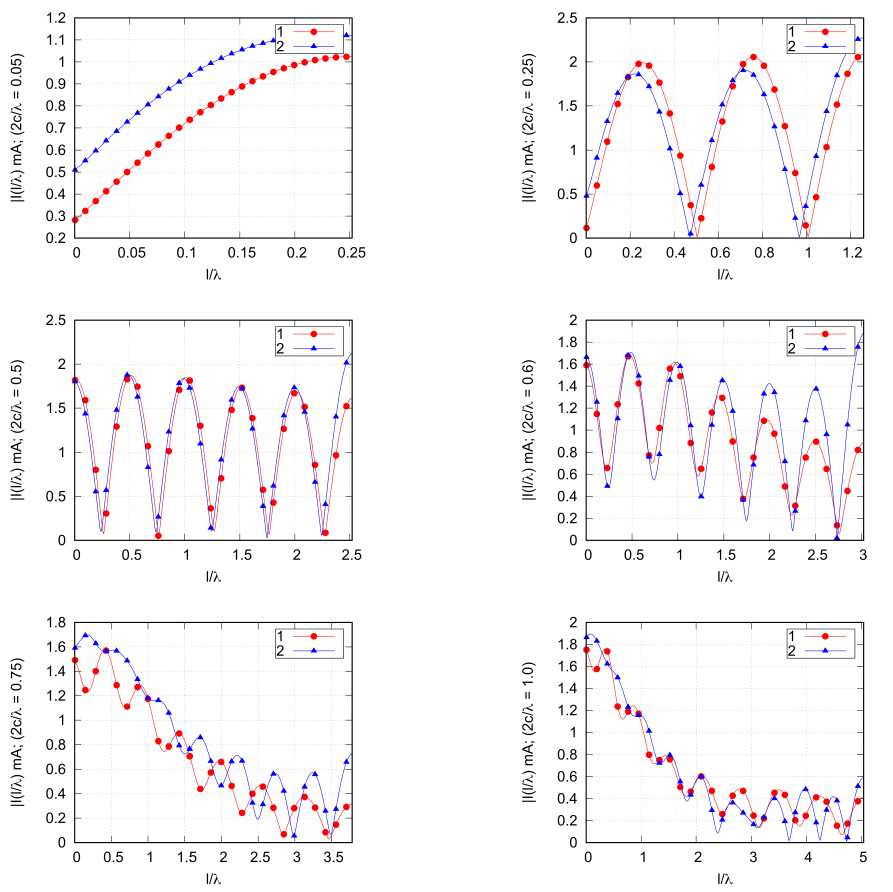
Рис. 2. Сравнение амплитудных распределений тока на проводнике AP А-спирали (кривая 1) и Б-спирали (кривая 2) при различных значениях 2 c / X ; a / c = 1/2
Fig. 2. Comparison of the amplitude distributions of the current on the conductor AP of the A-helix (curve 1) and B-helix (curve 2) at different values 2 c / X ; a / c = 1/2
емое рассматриваемыми структурами, но бегущие волны в А-спирали теряют энергию интенсивнее, чем в Б-спирали, отличия в результатах расчета для рассматриваемых структур становятся более заметными. При 2 c / X = 0,75, 1,0 излучение создается преимущественно бегущими волнами, амплитуда которых значительно падает с приближением к точке P . Здесь можно увидеть, что амплитуда стоячих волн в А-спирали вблизи точек A и A ′ заметно выше, но в целом распределения токов примерно совпадают.
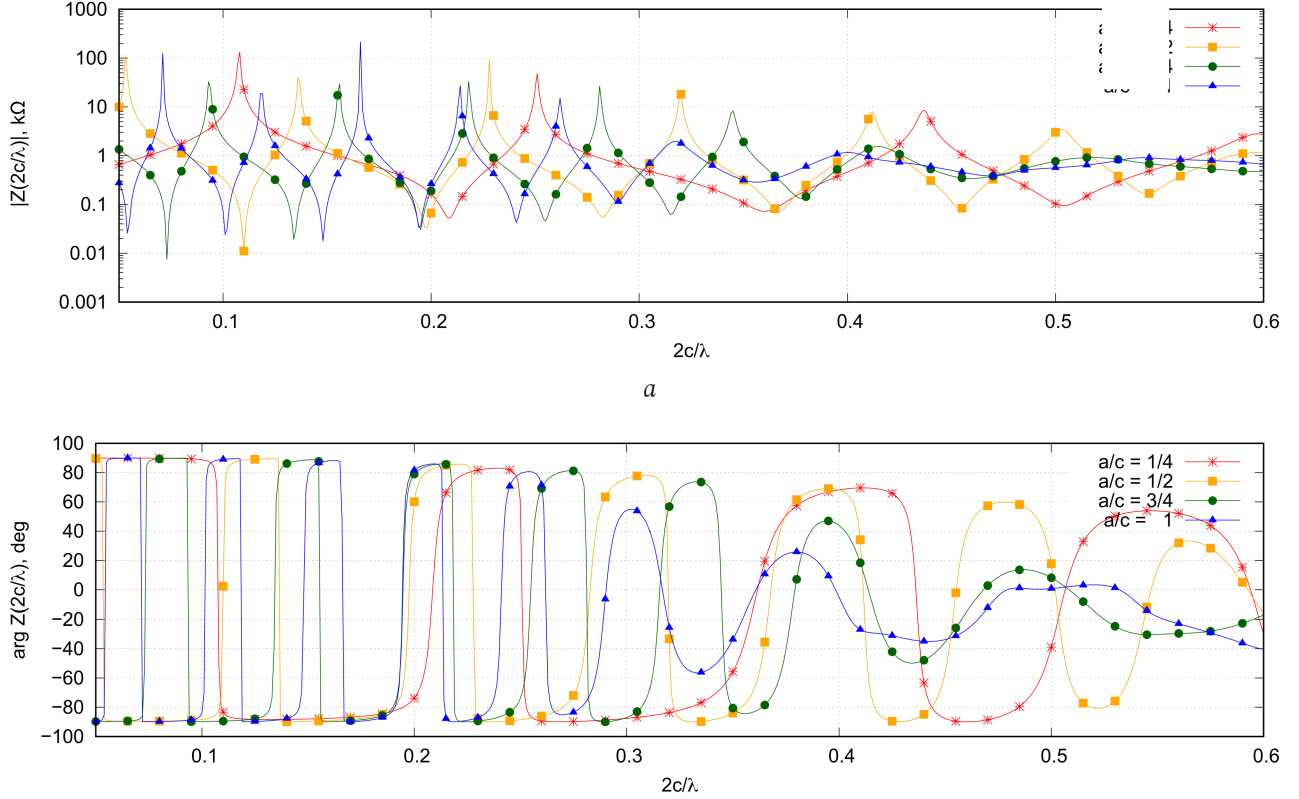
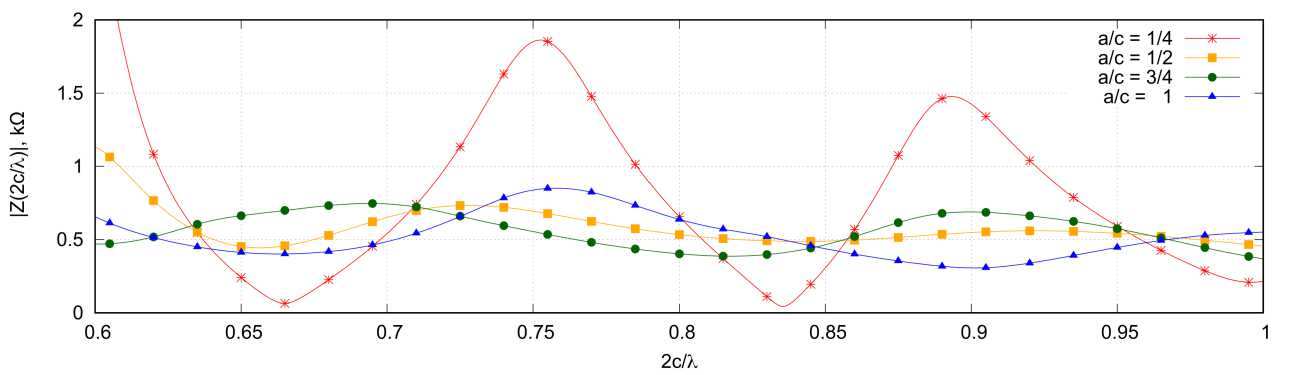
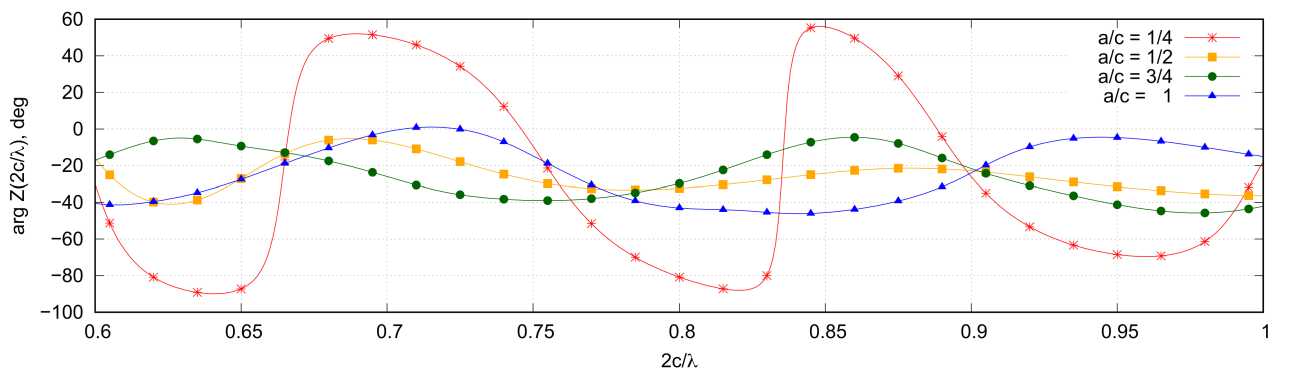
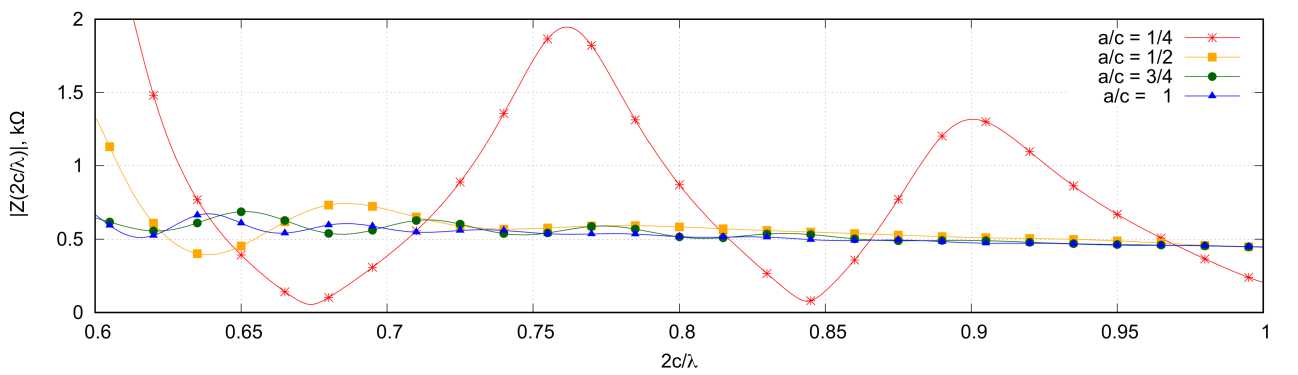
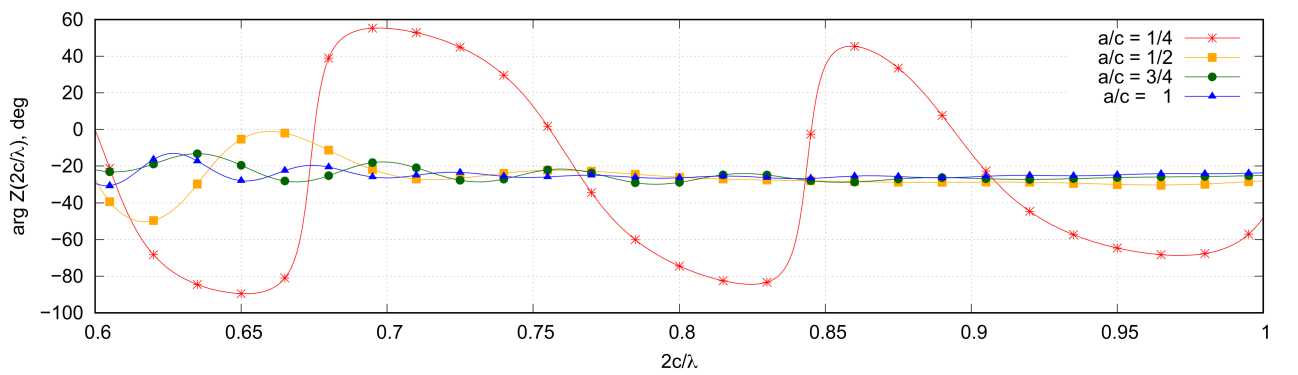
На рис. 3–6 приведены результаты расчета входного сопротивления рассматриваемых структур при четырех различных соотношениях a / c. С точки зрения входного сопротивления для этих структур можно условно выделить две области – низкочастотную (НЧ) и высокочастотную (ВЧ). В НЧ-области (рис. 3, 4) в распределении тока по проводникам преобладают стоячие волны, что формирует резонансный характер зависимости входного сопротивления от частоты. Добротность резонансов здесь имеет прямую зависимость от степени преобладания стоячих волн. Также, как видно из рис. 3, 4, она имеет обратную зависимость от отношения а / c. В целом зависимости входного сопротивления от частоты для А- и Б-спиралей в НЧ-области очень похожи.
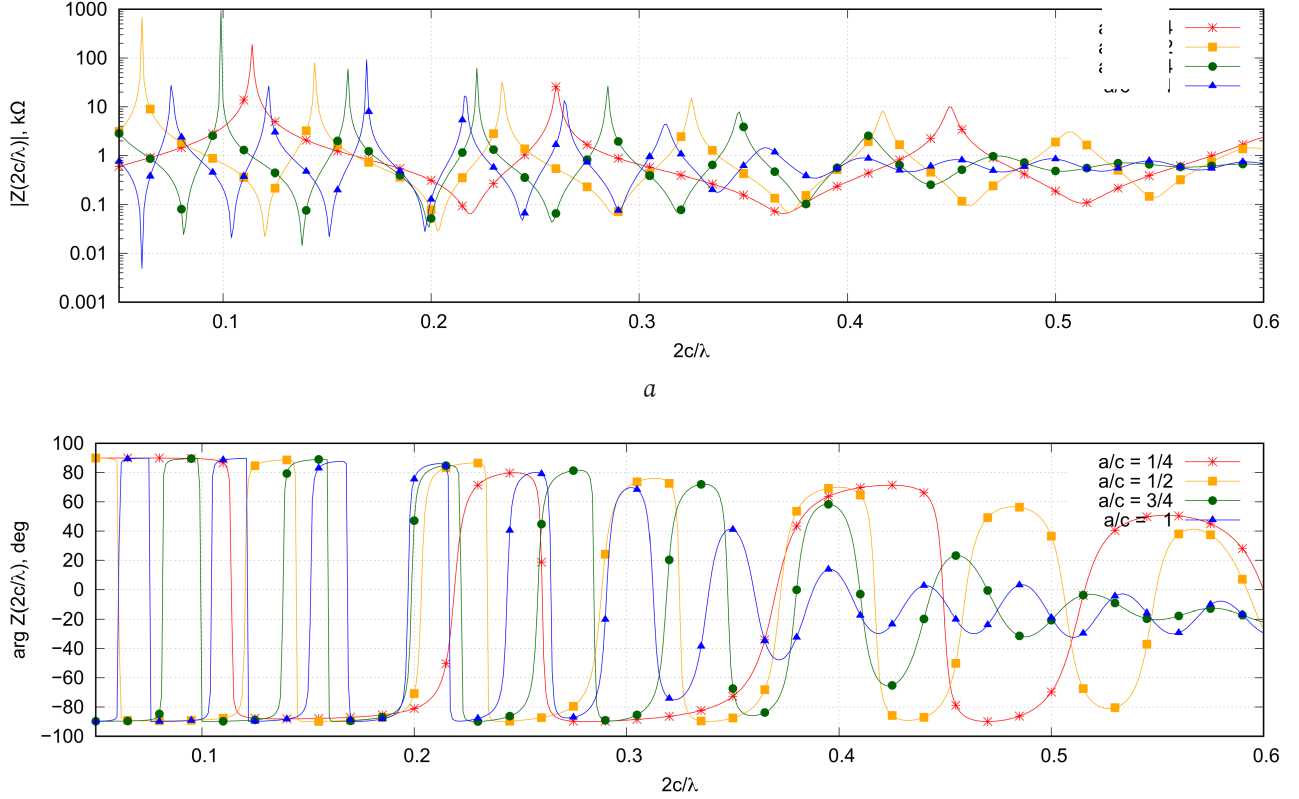
В ВЧ-области зависимость входного сопротивления от частоты при a / c >5 имеет более плавный характер (рис. 5, 6). Здесь можно отметить, что для Б-спирали равномерность входного сопротивления заметно выше, чем для А-спирали.
ale = 1/4 a/c = 1/2 a/c = 3/4 a/c = 1
б
a/c = 1/4 a/c = 1/2 a/c = 3/4 a/c = 1
Рис. 3. Зависимость амплитуды ( а ) и фазы ( б ) входного сопротивления от отношения 2 c / λ для А-спирали; 2 c / λ ∈ [0,05;0,6]
Fig. 3. Dependence of the amplitude ( a ) and phase ( b ) of the input resistance on the ratio 2 c / λ for the A-helix; 2 c / λ ∈ [0,05;0,6]
б
Рис. 4. Зависимость амплитуды ( а ) и фазы ( б ) входного сопротивления от отношения 2 c / λ для Б-спирали; 2 c / λ ∈ [0,05;0,6]
Fig. 4. Dependence of the amplitude ( a ) and phase ( b ) of the input resistance on the ratio 2 c / λ for the B-helix; 2 c / λ ∈ [0,05;0,6]
a
б
Рис. 5. Зависимость амплитуды ( а ) и фазы ( б ) входного сопротивления от отношения 2 c / λ для А-спирали; 2 c / λ ∈ [0,6;1,0]
Fig. 5. Dependence of the amplitude ( a ) and phase ( b ) of the input resistance on the ratio 2 c / λ for the A-helix; 2 c / λ ∈ [0,6;1,0]
a
б
Рис. 6. Зависимость амплитуды ( а ) и фазы ( б ) входного сопротивления от отношения 2 c / λ для Б-спирали; 2 c / λ ∈ [0,6;1,0]
Fig. 6. Dependence of the amplitude ( a ) and phase ( b ) of the input resistance on the ratio 2 c / λ for the B-helix; 2 c / λ ∈ [0,6;1,0]
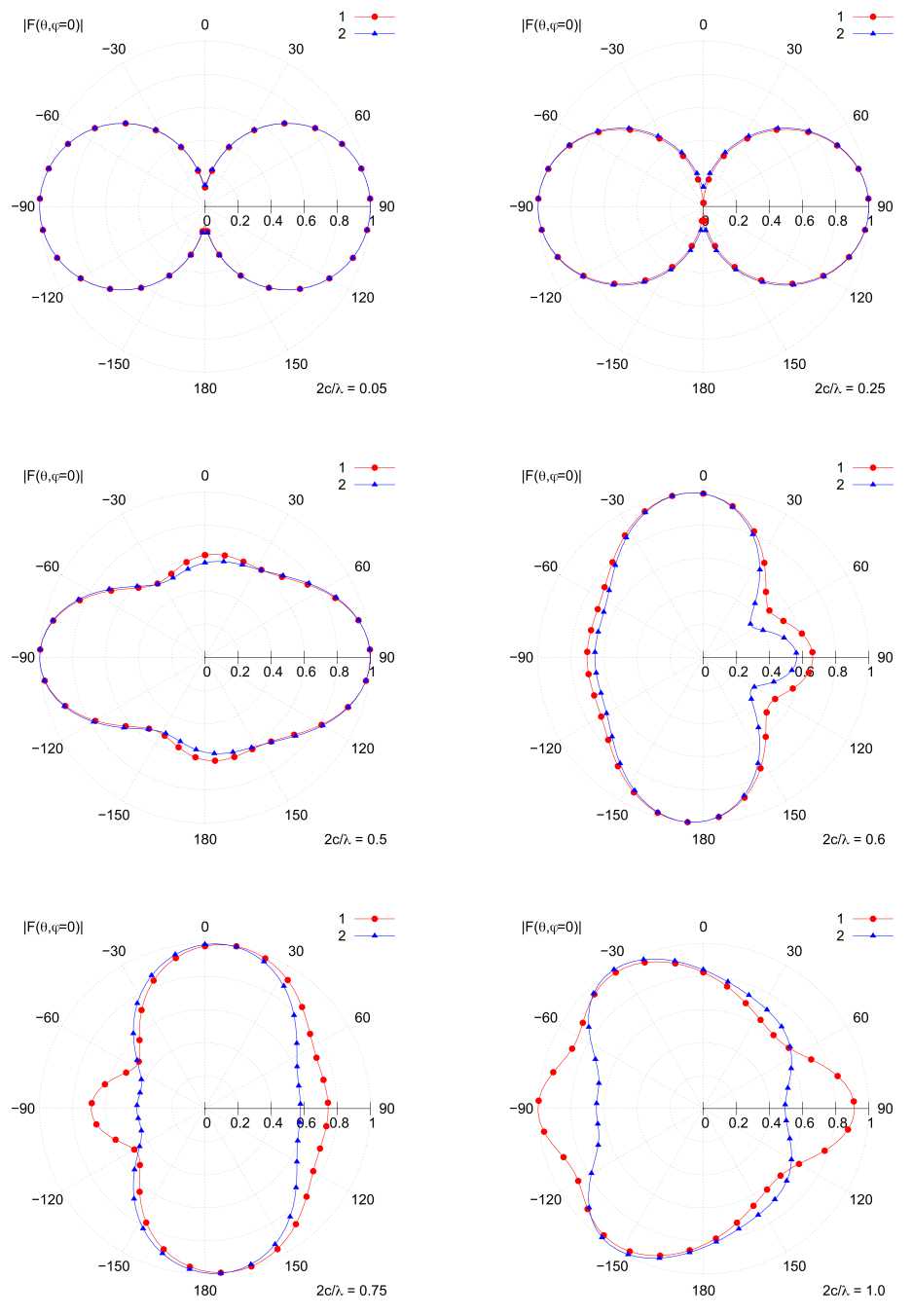
Рис. 7. Сравнение нормированных амплитудных диаграмм направленности А-спирали (кривая 1) и Б-спирали (кривая 2) при различных значениях 2 c / λ
Fig. 7. Comparison of the normalized amplitude radiation patterns of the A-helix (curve 1) and B-helix (curve 2) at different values 2 c / λ
Из рис. 5 видно, что для А-спирали с рассматриваемым числом витков имеется оптимальное значение a / c (в данном случае a / c = 0,5), при котором отклонение входного сопротивления от среднего значения будет минимальным. В ВЧ-диапазоне во входном сопротивлении рассматриваемых структур имеется емкостная составляющая входного сопротивления. При наименьшем рассматриваемом значении a / c , равном 1/4, частотная зависимость входного сопротивления во многом напоминает аналогичную зависимость для симметричного электрического вибратора.
На рис. 7 представлено сравнение нормированных амплитудных диаграмм направленности (ДН) рассматриваемых излучателей в меридианной плоскости, вычисленных при различных отношениях 2 c / X и фиксированном значении a / c = 1/2. При отношениях 2 c / X < 0,25 ДН имеет тороидальную форму, повторяющую аналогичную ДН симметричного вибратора. Это связано с тем, что поперечный размер излучателей гораздо меньше длины волны излучения. Здесь также можно наблюдать, что структура спирального проводника не оказывает существенного влияния на характеристики излучения и ДН А- и Б-спиралей совпадают с графической точностью. Дальнейшее увеличение 2 c / λ до 0.5 приводит к исчезновению нулей излучения в направлении оси A ′ A . При 2 c / X > 0,6 ДН приобретает форму, приближенную к сфероидальной. В этом случае также растут отличия в ДН А- и Б-спиралей.
Заключение
В работе рассмотрены два варианта сфероидальных спирально-рамочных излучателей (А-спираль и Б-спираль). Излучатели отличаются внутренней структурой спиральных элементов. Следует отметить, что спиральные антенны, обладающие геометрией, близкой к геометрии рассмотренных излучателей, широко применяются на практике. Предложены математические модели излучателей, построенные на основе интегрального представления электромагнитного поля, записанного в тонкопроволочном приближении. Данные
математические модели позволяют произвести количественную оценку электродинамических параметров рассматриваемых структур. Внутренняя задача сформулирована в виде системы интегральных уравнений Фредгольма первого рода. Приведен метод ее сведения к системе линейных алгебраических уравнений, записанной относительно неизвестных значений комплексных амплитуд тока на сегментах, а также приведено условие для корректного осуществления указанной процедуры.
На основе представленных моделей были получены численные решения для внутренней и внешней электродинамических задач. Для ряда отношений a / c в диапазоне значений 2 c / λ произведен расчет распределений тока, входного сопротивления и нормированных диаграмм направленности. Полученным результатам дана физическая интерпретация. Показано, что в рассмотренных структурах в зависимости от отношения 2 c / λ может быть реализован режим стоячей, бегущей или смешанной волны тока. Режим стоячей волны возникает при малых 2 c / X , режим бегущей волны характерен для 2 c / X >3/4. Анализ зависимости входного сопротивления от 2 c / λ показал тесную взаимосвязь между токовым режимом и характером поведения входного сопротивления. Также в процессе анализа результатов по входному сопротивлению установлено, что большей равномерностью входного сопротивления при 2 c / X > 0,6 обладает Б-спираль, а для А-спирали имеется оптимальное отношение a / c , при котором достигается его минимальная неравномерность. Анализ характеристик излучения показал, что при малых отношениях 2 c / λ нормированные ДН совпадают по форме с ДН симметричного электрического вибратора, при увеличении 2 c / λ ДН приобретает форму, близкую к эллипсоидальной. В дальнейшем авторы планируют повысить вычислительную эффективность предложенных моделей с помощью применения оптимальных систем проекционных функций и провести более детальный анализ численных результатов при различных отношениях геометрических параметров структур.
Список литературы Математические модели сфероидальных спирально-рамочных излучателей
- Рамсей В. Частотно-независимые антенны. М.: Мир, 1968. 176 с.
- Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. Изд. 2-е, доп. и перераб. М.: Сов. радио, 1974. 536 с.
- Физический энциклопедический словарь / под ред. А.М. Прохорова. М.: Большая российская энциклопедия, 1995. 928 с.
- Неганов В.А., Осипов О.В. Отражающие, волноведущие и излучающие структуры с киральными элементами. М.: Радио и связь, 2006. 280 с.
- Аралкин М.В., Дементьев А.Н., Осипов О.В. Математические модели киральных метаматериалов на основе многозаходных проводящих элементов // Физика волновых процессов и радиотехнические системы. 2020. Т. 23, № 1. C. 8–19. DOI: https://doi.org/10.18469/1810-3189.2020.23.1.8-19
- Осипов О.В., Почепцов А.О., Антипова Т.А. Электродинамика планарных отражающих структур с киральными слоями на основе тонкопроволочных спиральных элементов // Физика волновых процессов и радиотехнические системы. 2018. Т. 21, № 3. С. 59–65. URL: https://journals.ssau.ru/pwp/article/view/7019
- Юрцев О.А., Рунов А.В., Казарин А.Н. Спиральные антенны. М.: Сов. радио, 1974. 223 с.
- Mei K. On the integral equations of thin wire antennas // IEEE Transactions on Antennas and Propagation. 1965. Vol. 13, no. 3. P. 374–378. DOI: https://doi.org/10.1109/TAP.1965.1138432
- Adekola S., Mowete A., Ayorinde A. Compact theory of the broadband elliptical helical antenna // European Journal of Scientific Research. 2009. Vol. 31, № 3. P. 446–490.
- Чебышев В.В. Микрополосковые антенны в многослойных средах. М.: Радиотехника, 2007. 160 с.
- Неганов В.А., Табаков Д.П. Математические модели цилиндрической спиральной антенны // Физика волновых процессов и радиотехнические системы. 2013. Т. 16, № 4. С. 79–86.
- Стрижков В.А. Математическое моделирование электродинамических процессов в проволочных антенных системах // Математическое моделирование. 1989. Т. 1, № 8. С. 127–138. URL: https://www.mathnet.ru/rus/mm/v1/i8/p127
- Неганов В.А. Интегральное представление электромагнитного поля геометрически киральной структуры // Физика волновых процессов и радиотехнические системы. 2012. Т. 15, № 4. С. 6–13.
- Табаков Д.П. Об описании излучения и дифракции электромагнитных волн методом собственных функций // Известия вузов. Радиофизика. 2021. Т. 64, № 3. С. 179–191. URL: https://radiophysics.unn.ru/issues/2021/3/179
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. M.: Бином; Лаборатория знаний, 2008. 686 с.
- Неганов В.А., Нефедов Е.И., Яровой Г.П. Электродинамические методы проектирования устройств СВЧ и антенн / под ред. В.А. Неганова. М.: Радио и связь, 2002. 416 с.
- Табаков Д.П., Морозов С.В., Клюев Д.С. Применение тонкопроволочного интегрального представления электромагнитного поля к решению задачи дифракции электромагнитных волн на проводящих телах // Физика волновых процессов и радиотехнические системы. 2022. Т. 25, № 2. С. 7–14. DOI: https://doi.org/10.18469/1810-3189.2022.25.2.7-14


