Математические основы онтологии проектирования бинарных систем обработки информации

В работе [1], посвященной анализу различных вопросов, связанных с современными онтологиями проектирования сложных технических систем и, в частности, формализации знаний в таких системах, облегчающих их автоматическую алгоритмическую обработку, отмечается, что «…проблема перевода имеющихся знаний в форму, пригодную для машинной обработки, все ещё актуальна и зачастую препятствует практической реализации систем интеллектуальной поддержки» (задач проектирования). На важность математики в исследовании различных аспектов прикладных онтологий обращал также внимание В. Г. Черняков [2]. В работе [3] рассмотрен ряд особенностей, связанных с математическими основами онтологии проектирования гетерогенных электронных систем обработки информации на базе нового направления общей теории систем (ОТС), получившего название «Общая формальная технология» (ОФТ). ОФТ изучает формальные алгоритмы над реальными объектами или их достаточно адекватными математическими моделями, а также поведение самих таких моделей на основе реализуемых ими функциональных взаимодействий объектов между собой [3, 4]. Предлагаемый на основе подобных ОФТ-концепций подход позволяет, во-первых, ввести единообразные математически-обоснованные модели, объясняющие функционирование как гомогенных, так и гетерогенных систем обработки двоичной (бинарной) информации, и, во-вторых, существенно расширить пространство потенциально-полезных схемотех- нических решений за счёт использования для реализации нужных вычислительных функций опять же не только гомогенных, но и разнотипных (гетерогенных) сигналов, включая гетерогенные (разнородные) параметры различных электронных компонентов и функциональных блоков (ФБ). Например, в [3] показано, что для двухвходовых ФБ с гетерогенными входными и выходными сигналами или параметрами пространство таких потенциально-полезных схемотехнических решений при проектировании электронных бинарных систем можно увеличить примерно в 3000 раз.

С другой стороны, в [5] на основе этого же подхода предпринята попытка объяснить логику обработки информации в системах «химического типа», т.е. в системах различных химических реакций, широко используемых природой для реализации самых разнообразных процессов контроля и управления, а также в процессах синтеза и анализа нужных молекул в биологических организмах. Для обоснования булевской функциональной полноты таких систем использован классический метод сведения различных химических преобразований к традиционным двоичным функционально-полным наборам логических функций. В то же время в работе [4] показано, что уже в самом простом формальном варианте описаний различных бинарных преобразований сигналов из пяти теоретически-возможных гомогенных и гетерогенных взаимодействий обычной, классической (т.е. гомогенной) логике соответствует только один. Каковы же самые общие критерии функциональной полноты именно таких -гетерогенных систем обработки информации - при различных, желательно максимально простых (или наиболее очевидных, наиболее «естественных») функциональных зависимостях выходных сигналов (параметров) от входных?

Чтобы разобраться в этих вопросах, напомним некоторые особенности ОФТ-подхода к представлению различных физических объектов и их функциональностей. Согласно ему, любой физический объект O i в ОФТ формально представляется в виде двух конечных множеств-списков:

• (1)    O i = < y i , M i > = <{ y i , Y 2 ,..., Y in }, { Y ij = ф у ( Y sk , Y i ,-, Y sm );•••}>,

где y i - множество (список) интересующих нас свойств объекта, или параметров (обозначенных символами типа Y ik ), включая, например, геометрические свойства, описывающие форму объекта, его положение в пространстве и даже (при необходимости) направление, скорость движения и, к примеру, массу и/или цвет; M i - множество (список) интересующих нас функ-циональностей ф у объекта O i (эти функциональности могут быть записаны в любой удобной форме - в виде функций, физических законов, алгоритмических процедур и т.д.); n - число параметров (свойств), используемых в данном представлении объекта O i ; j , l е {1,..., n }; k, m - номера (вторые индексы) тех свойств и функциональностей, которые актуальны для анализа функциональных взаимодействий ф у данного объекта O i (в текущем представлении) с соседними (или удалёнными - если речь идёт о взаимодействии, например, через поле) объектами типа O s , причём в общем случае значение некоторого параметра (свойства) Y ij объекта O i может зависеть как от параметров самого этого объекта (т.е. от свойств типа y il самого объекта O i ), так и от параметров (свойств) y _sk других объектов типа O s , контактирующих с данным объектом O i или удалённых от него (точнее - удалённо-взаимодействующих с O i ). Подчеркнём, что функциональных зависимостей фу в списке функциональностей M i объекта O i может быть столько, сколько нужно для его адекватного представления в рамках данной модели, на что указывает многоточие после формулы для ф у при расчёте параметров y ij . Однако всегда в конечном представлении любого объекта типа O i это число конечно [4].

1 Предварительные замечания

В соответствии с рассмотренным выше подходом формальное представление какого-либо двухвходового логического элемента (например, типа «2И-НЕ») может быть записано следующим образом:

• (2)         O 2И-НЕ - < Y 2И-НЕ , М 2И-НЕ > = <{ Y 1 , Y 2 , Y s }, { Y 3 = 0 2И-Не(Л Y 2 )--( Y 1 Л Y ? )}>,

где символ «-» (минус) означает инверсию результата операции в скобках, « л » - символ конъюнкции, Y 1 , Y 2 , Y 3 ^е {0, 1}, а нижние индексы обозначают тип того логического элемента, к которому относится данное множество (элементов, свойств или функциональностей).

Используя обозначения, принятые в [4], тип формальных функциональных преобразований, использованный в (2), можно записать следующим образом:

(Y1)i2И-НЕ * (Y?)i2И-НЕ ^ (Ys)i™, где нижний индекс i означает, что все три параметра в скобках (Y1), (Y2) и (Y3) (соответствующие текущим значениям двух входных логических сигналов Y1, Y2 и одному выходному - Y3) относятся к одному и тому же виду их физических носителей или параметров, то есть гомогенны; верхние индексы (символы «2И-НЕ») просто обозначают сам тип объекта (логического элемента «2И-НЕ»), к которому относится данный параметр, символ звездочки «*» обозначает некое (в общем случае - любое) функциональное взаимодействие двух входных параметров Y1 и Y2, стрелка «^» указывает направление функциональных преобразований, а последний компонент «(ys)j2И-НЕ» в (3) - их результат (в виде значения параметра Y3). С некоторой долей условности можно считать, что параметры Y1, Y2, Y3 есть некие физические свойства логических элементов типа «2И-НЕ», в совокупности определяющие его состояние [4]. Схематически такое взаимодействие двух входных параметров-сигналов Y1, Y2,, формирую щих в итоге этого (взаимодействия) значение некоего выходного параметра-сигнала Y3, для соответствующего объекта с двумя входами и одним выходом O2-1, можно представить так, как это показано на рисунке 1.

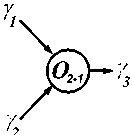
Рисунок 1 - Условное обозначение функционирования некоего объекта с двумя входами и одним выходом

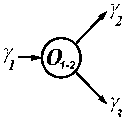
Рисунок 2 - Функция разветвителя в самом общем виде

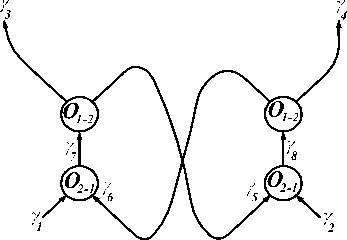
Рисунок 3 - Общая схема гетерогенного бинарного триггера

Для удобства и простоты сопоставления с реальными логическими элементами можно считать, что физическими носителями этих параметров могут быть, например, два уровня напряжений, соответствующих нулю и единице, или два уровня тока, или два уровня частоты сигнала и т.п. Обозначая аналогично все возможные типы функциональных преобразований, можно, согласно [4], для объектов типа O _2-1, (т.е. для объектов с двумя условновходными физическими параметрами Y 1 и Y 2 , и одним условно-выходным параметром Y 3 ) записать:

f I ^ I I

(4.1)

(4.2)

(4.3)

(4.4)

(4.5)

00 Р *0» O ^ ⁽ / 3> Р ( п )^р *00 к ⁰ ^ (я) ^Р (я) ° ‘ to O ^ (я) ° ( Y i )^p ‘ to к ⁰ ^ (я) .° (и) ^р ‘ toР ^ (Я) к ⁰

где различные нижние индексы i , к , 5 соответствуют различным , то есть не зависимым друг от друга, а, следовательно, с математической точки зрения ортогональным друг к другу, фи-

зическим параметрам.

Ещё раз отметим, что тип функционального взаимодействия, использованный в функционировании бинарных гомогенных логических элементов вида (2), соответствующий общему выражению (3), реализуется только в выражении (4.1) системы (4), тогда как остальные 4 типа функциональных взаимодействий (4.2)-(4.5) относятся, во-первых, к взаимодействиям гетерогенного типа, а, во-вторых, в случае симметричности двух входных физических параметров i и к , выражения (4.2) и (4.3) описывают фактически один и тот же их тип.

2    Новые результаты

Какую же простейшую математическую зависимость должны носить функциональные преобразования в списке M i некоего объекта, чтобы он в принципе мог использоваться как базовый объект для формирования функционально-полных систем логических функций подобно логическим элементам типа «2И-НЕ»? Как известно [3], эти логические элементы могут обеспечить функциональную полноту набора логических функций вместе с константами «0» (или «1»), и в совокупности с ещё одним функциональным блоком, названным в [3, 5] «разветвителем» (сигналов или параметров) - см. рисунок 2.

Заметим, что в отличие от «разветвителей» в работах [3, 5], «разветвитель сигналов (параметров)» на рисунке 2 не обязательно генерирует на выходе два эквивалентных сигнала (параметра). Это могут быть в принципе любые гетерогенные сигналы-параметры или даже разные физические объекты [5]. Обозначим соответствующий ФБ как объект типа O _1-2.

С учётом наиболее простых конкретных вариантов реализации функций (функциональ-ностей) разветвителя один из них можно математически записать следующим образом:

• (5)    Если Y 1 > Y 1c , то ( y >>  Y 2c )&( Y >>  Y 3c ), иначе ( y <<  Y >c )&( Y <<  Y 3c ),

где y _1c , y _2c, Y 3_c — некоторые «пороговые» значения («константы») для параметров Y 1 , Y 2 и Y 3 соответственно.

Другой вариант:

• (6)    Если Y 1 >  Y 1c , то ( Y 2 >>  Y 2c )&( Y >>  Yc ), иначе ( y * 0 )&( y * 0 ),

где 0 - символ отсутствующего («пустого» или «близкого к нулю») параметра (собственно, знак приближенного равенства « * » говорит об этом же.). Возможны и иные сочетания, которые мы ввиду их практически одинакового смысла пока рассматривать не будем.

Если вновь обратиться к внутренней сущности правой части формулы (2) в контексте выражения (3), то можно утверждать, что метод (функциональность) М2И-НЕ реализует некую разновидность «инвертированной пороговой функциональности». Действительно, при традиционном толковании всех выражений в (4) если каждый из входных параметров (Y1)i и (y)i превышает некоторый фиксированный уровень, условно соответствующий «1», то только в этом случае выходной параметр (Y3)i становится равным «нулю» (или просто отсутствует). В противоположном случае «выход» (y)i остается «активным», т.е. «генерирует» уровень параметра (Y3)i, условно соответствующий «единице» (что обычно связывается с наличием дан- ного параметра на «выходе» объекта). Таким образом, получается, что суммарная (итоговая) функциональность для (2) легко формируется последовательной композицией двух более простых функциональностей - чисто «пороговой» для двух входных параметров и чисто «инвертирующей» - для выходного. Заметим при этом, что «инверсию» значения некоторого физического параметра увх i всегда можно реализовать путём простого преобразования одного уровня одного параметра в другой по следующей схеме:

f Х вых.1 , если ^ вх i ^> ^Y c i

• (7)                           / вых = ^

I /вых.2, иначе, где Yc i - некоторое (обычно не крайнее) значение некоторого физического параметра из области допустимых значений для ybx i, а Yвых1 и Yвых2 — аналогичные допустимые (но не обязательно равные друг другу!) значения из области допустимых для Yвых. При этом не имеет никакого значения, какой из выходных параметров Yвых1 и Yвых2 больше другого. Заметим также, что физические параметры ybx i и Yвых могут быть как одной природы (для гомогенных функциональных преобразований), так и разной (для гетерогенных), а само выражение (7) с очевидностью описывает всё ту же «пороговую функциональность» для некоего гипотетического «одновходового (с одним выходом)» объекта O1.1. Ясно, что такой объект легко реализовать на основе любого «двухвходового» объекта O2-1, входящего в систему различных типов функциональных преобразований (4) - если сделать один из входных «сигналов-параметров» какого-либо объекта в ней постоянным (то есть константой). Сама же функциональность двухвходового порогового элемента O2-1 для рассматриваемого случая может быть записана так:

f Y 3-1 , если ( y i >  Y 1g ) a ( y? >  Y >g )

• (8)                        Y 3 = ^

I Y 3-2 , если ( Y 1 <  Y 1g ) v ( y <  Y >g);

где y _3-1, Y 3 _-2 — различные значения (например, уровни) выходного параметра Y 3 , а y _1g и y ?_g — по прежнему некоторые пороговые значения для входных параметров Y 1 и Y 2 . Нетрудно видеть, что в общем случае возможны также смена типа выходного параметра Y 3 - формула (9), или его полное «выключение» - формула (10):

f Y 3-1 , если ( Y 1 >  Y 1g ) a ( y? >  Y 2g )

• (9)                        Y 3 = ^

I Y 4 , если ( Y 1 <  Y 1g ) v ( y <  Y >g );

f Y 3-1 , если ( Y 1 >  Y 1g ) a ( y> >  Y 2g )

• (10)                     Y 3 = ^

I 0 , если ( Y 1 <  Y 1g ) v ( y <  Y >g );

где 0 - символ пустого (отсутствующего, «выключенного») выходного параметра Y 3 .

С другой стороны, легко заметить, что в отношении самих параметров Y 1 и Y 2 все три выражения (8)-(10) описывают логическую функцию типа «И». Действительно, только при наличии и первого, и второго входных параметров Y 1 и Y 2 со значениями, превышающими пороговые, на выходе O _2-1 формируется выходной сигнал-параметр у 3 . Другие возможные типы логических взаимодействий по этим входным параметрам (например, «ИЛИ», «Исключающее ИЛИ» и т.д.) представляются более сложно устроенными, поэтому пока не рассматриваются.

С учётом «инверсии» типа (7) можно заключить, что при определённых условиях практически любое выражение системы (4) для «двухвходовых с одним выходом» функциональ- ных объектов может служить базовым, делающим в принципе возможным достижение булевской функциональной полноты [5]. Ограничивающим условием здесь служит только факт существования объектов, которые могут связываться по своим выходным и входным параметрам-сигналам друг с другом в соответствующие сети. Например, сеть таких гетерогенных объектов, соответствующая схеме обычного двоичного гетерогенного триггера, с учётом вышесказанного, может условно изображаться как показано на рисунке 3.

Легко проверяется, что триггер (см. рисунок 3) работает при любой из приведённых выше интерпретаций функциональностей объектов O 2-1 (8)-(10) и разветвителей O 1-2 . (5)-(6).

Кроме того, все восемь параметров ( γ 1 - γ 8 ), необходимые для работы такого триггера, могут быть различными по своей физической сути, т.е. гетерогенными, однако это условие не является жёстким, обязательным. Некоторые из них вполне могут быть и гомогенными, например, γ 1 и γ 2 , γ 3 и γ 6 , и даже γ 1 , γ 4 и γ 5 , включая все γ 1 - γ 8 .

Аналогичным образом могут быть сконструированы трёх-стабильные триггеры, и вообще – любые n -стабильные запоминающие устройства, где n – любое (конечное) целое число. Правда, для их реализации потребуются объекты с большим числом входов: от типа O 3-1 до типа O ( n+ 1)-1 и соответствующие разветвители. Впрочем, как показано в [3, 5], разветвители (с функциональностями «порогового» типа) на любое количество выходов, как и многовходовые схемы совпадения наличия параметров на любое конечное их число, могут быть реализованы каскадным включением соответствующих объектов типа O 1-2 и O 2-1 (рисунок 4).

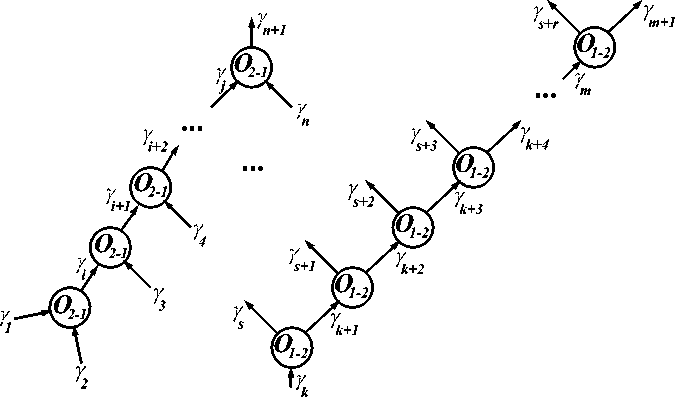
Рисунок 4 - Многовходовая схема совпадения (слева) и разветвитель (справа) на любое конечное число входов и выходов

3    Основные теоремы

Рассмотренные выше особенности различных компонентов бинарных систем обработки информации с максимально широким диапазоном физических реализаций позволяют сформулировать следующие базовые теоремы, называемые далее утверждениями.

Утверждение 1. Любая конечная булева функция (бинарная комбинационная схема) может быть реализована подходящей конечной сетью функциональных объектов типа O 2-1 и O 1-2 с функциональностями «порогового» типа, связанными между собой по индивидуальным уникальным входным-выходным параметрам (сигналам).

Доказательство . Действительно, любая конечная булева функция может быть реализована в виде дизъюнктивной нормальной формы (ДНФ), представляющей собой конечную дизъюнкцию конечных же конъюнкций [6]. Представим все конъюнкции, входящие в соответствующую ДНФ, в виде подходящих сетей функциональных объектов типа O 2-1 и O 1-2 , связанных надлежащим образом между собой по индивидуальным уникальным входным-выходным параметрам (сигналам) – см. рисунок 4. Сопоставим каждый уникальный индивидуальный выходной параметр соответствующей схемы совпадения (типа приведённой на рисунке 4 слева) с тем выходным сигналом, за который отвечает соответствующая конъюнкция ДНФ, а все входящие в эту конъюнкцию двоичные переменные – с соответствующими входными параметрами нашей схемы совпадения. Это всегда можно сделать, поскольку по условиям утверждения 1 мы всегда можем назначать нашим входным и выходным параметрам входящих в сеть объектов «индивидуальные уникальные имена», а с помощью сетей типа «разветвителей» (рисунок 4) получить столько реплик исходных физических параметров-сигналов, сколько необходимо.

В итоге мы получим сеть, на выходах которой будут формироваться именно те выходные параметры, которые соответствуют логическим единицам на выходах соответствующих конъюнкций при наличии требуемого набора их входных логических переменных, т.е. сеть, эмулирующую нашу ДНФ. Таким образом, утверждение доказано.

Справедливость утверждения 1 вместе с рассмотренной ранее возможностью реализовать в аналогичных сетях многоустойчивые элементы памяти позволяет сформулировать также следующее.

Утверждение 2. Любой детерминированный конечный автомат (обработки информации) может быть реализован подходящей конечной сетью функциональных объектов типа O 2-1 и O 1-2 с функциональностями «порогового» типа, связанными между собой по индивидуальным уникальным входным-выходным параметрам (сигналам).

Доказательство. Детерминированный конечный автомат может быть реализован либо как автомат Мили, либо как автомат Мура [7]. Поскольку оба автомата эквивалентны, рассмотрим в качестве основного автомат Мили. Он содержит конечный набор триггеров (память состояний) и комбинационную схему, реализующую функции переходов и выходов, т.е. переключение состояний в зависимости от текущего состояния и кода входного символа, и формирующую коды выходных символов в зависимости от этих же параметров (рисунок 5). Оба этих конечных функциональных блока вполне реализуемы в рамках рассмотренных выше функциональностей (рисунки 1-4). Утверждение доказано.

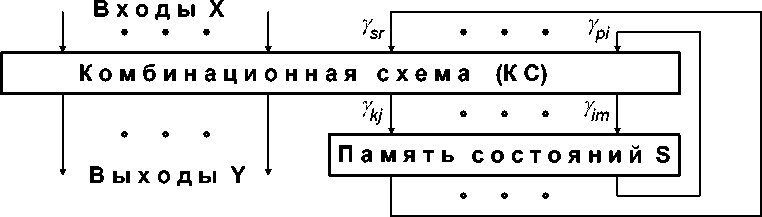
Рисунок 5 - Структурная схема автомата Мили

4    Обсуждение

Очевидно, что рассмотренные в утверждениях 1 и 2 гетерогенные бинарные системы обработки информации (ГБСОИ) являются функционально-полными с точки зрения класса булевских функций, несмотря на то, что они не содержат в явном виде никакие классические функционально-полные (под)классы таких функций.

Самое неожиданное свойство рассмотренных ГБСОИ – то, что для достижения булевской функциональной полноты им не нужна логическая инверсия. Аналогичная особенность отмечалась и в преобразованиях «химического типа» при исследовании вопросов их функциональной полноты [4, 5]. Роль инверсии в ГБСОИ выполняет либо конкретный и уникальный уровень выходного параметра (сигнала), либо смена типа самого этого параметра. Выше уже отмечалось, что разные типы таких параметров с точки зрения математики следует рассматривать, как ортогональные. Таким образом, необходимая для достижения булевской функциональной полноты функция логической инверсии реализуется здесь в многомерном пространстве ортогональных физических свойств (параметров) путём некоего (функционального) отображения параметра одного типа на параметр другого (ортогонального) типа.

Другой интересный аспект рассматриваемых ГБСОИ – возможная интерпретация необходимости уникальных индивидуальных физических свойств-параметров, связывающих объекты-элементы в сети и выполняющих роль уникальных (индивидуальных) сигналов. В работах по ОФТ отмечалось [4], что с формально-технологической точки зрения такими уникальными индивидуальными физическими параметрами объектов могут быть, во-первых, их пространственное положение (в двухмерном, а лучше – в трёхмерном пространстве), во-вторых - форма и структура (состав) объектов (например, физико-химический). Вторая интерпретация приводит к выводу о том, что с представленной точки зрения соответствующие цепочки химических реакций также могут обладать булевской функциональной полнотой и, естественно, поэтому могут кодировать сложные процессы обработки информации химического типа [4, 5], в которых входные и выходные символы-сигналы представляют собой те или иные химические вещества – молекулы. Как известно, этот вариант широко используется природой для своих самых необычных и самых сложных конструкций – живых существ [8].

Если же воспользоваться первым вариантом интерпретации, то приходим к более гомогенным структурам – в частности, к структурам, близким к структуре головного мозга [9]. В них роль уникальных физических параметров-сигналов, как уже отмечалось выше, играют уникальные пространственные (обычно трёхмерные) физические координаты элементарных объектов обработки информации - клеток-нейронов. При этом надобность в гетерогенных типах самих сигналов отпадает, что делает структуру мозга более простой с точки зрения её физической реализации. Кстати - те же самые причины (простота) заставляют и нас использовать для реализации своих систем обработки информации аналогичные (гомогенные по типам сигналов) подходы.

Заметим, что даже мозг ребенка уже изначально содержит структуры, аналогичные упомянутым в утверждениях 1 и 2 [10]. То есть уже изначально структура мозга состоит из многоустойчивых элементов памяти и комбинационных схем. Другое дело, что в процессе обучения (настройки) этой начальной структуры на конкретные важные объекты и события некоторые из уже имеющихся первоначальных связей оказываются не нужными. Такие связи со временем деактивируются, то есть разрываются. При этом скорость такой деактивации оказывается довольно высокой – примерно до 12,5 триллионов связей в год или более 34 миллиардов в день (то есть в среднем чуть менее 400 тысяч связей в секунду). Однако перед этим – в раннем возрасте (до 3-х лет) устанавливаются новые – полезные – связи со скоростью до примерно 2 миллиона в секунду [10]!

Заключение

Таким образом, прикладная онтология проектирования самых различных бинарных систем обработки информации действительно имеет в своей основе общую математическую базу, подтверждающую эффективность использования математики при онтологическом анализе таких систем.

Рассмотренный подход к оценке структур и типов функциональностей для реализации как гомогенных, так и гетерогенных бинарных систем обработки информации и их компонентов на основе предложенной в ОФТ концепции формального представления любых объектов в виде (1), показал свою эффективность и состоятельность, что подтверждает факт целесообразности использования метаматематического аппарата ОФТ при исследовании различных физических и интеллектуальных процессов окружающего мира, включая потенциальные возможности самой математики. Оказалось, что с позиций ОФТ привычные нам гомогенные системы обработки информации на основе булевской логики и часто используемые в живой природе гомогенные (опять же по типам информационных сигналов) структуры типа нейросетей, и даже различные цепочки гетерогенных химических реакций, оказываются вполне равноправными по своим информационно-функциональным возможностям, сопоставимыми с аналогичными возможностями функционально-полных наборов булевских функций. Это позволяет подойти к разработке и проектированию самых разнообразных, в том числе гетерогенных, систем обработки информации с принципиально новых, несколько непривычных и неожиданных позиций [3, 4].