Математические основы робототехники

Для того чтобы математически описать движение мобильного робота нам потребуется определить системы координат. Введем две системы координат - мировую систему координат W (будем считать что он неподвижна в пространстве), и система координат робота R , которая перемещается в пространстве и остается неподвижной относительно самого робота (рис. 1).

Рис. 1. Системы координат

Если предположить, что робот ограничивается перемещением на плоскости [1], его местоположение может быть определено вектором состояниях, состоящим из трех параметров:

f x 1

X = у

16 J хи у определяют местоположение предопределенной точки «центра робота» в мировой системе координат.

9 определяет угол поворота между системами координат (угол между осями X W и X R ).

Две системы координат совпадают в момент, когда центр робота находится в начале координат и x = y = ⁶ = 0 .

Получая перемещения робота в некоторые моменты времени, мы можем найти весь путь, пройденный роботом, просуммировав эти значения, или перейдя к пределу (при стремлении количества измерений ^да) - путем их интегрирования.

При движении на плоскости имеем три степени свободы для определения положения, представленные ( x , у , 6) при п < 6 <  п .

Рассмотрим робота, который может только двигаться вперед или поворачиваться на месте:

При прямолинейном движении робота на расстояние D новое состояние будет выражено как:

x new y"'

V ⁶ new /

^ x + D cos 6

= у + D sin 6

А

V ⁶    7

Если присутствует только вращательное движение, при повороте на угол

а:

x new

new

А

V new 7

Г x )

у

V 6 + а,

Рассмотрим математические принципы работы некоторых видов приводов.

1)дифференциальный привод

Робот с дифференциальным приводом имеет два мотора, по одному на каждое колесо. Изменение направления движения достигается за счет разных скоростей (отсюда и название - дифференциальный) [2]:

-Для прямолинейного движения колеса должны вращаться с одинаковыми скоростями.

-Для того, чтобы робот развернулся на месте, необходимо установить скорости одинаковыми по модулю, но направленными противоположно.

-Другие комбинации скоростей приводят к движению по дуге (рис. 2).

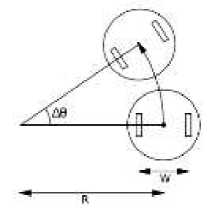
Рис. 2. Движение по дуге

Обозначим скорости колес (линейные скорости с которыми они «покрывают» поверхность) V L и V R - для левого и правого колес, соответственно, и W расстояние между колесами.

-Прямолинейное движение, если V L = V R .

-Разворот на месте, если V L = - V R .

• -В более общем случае - движение по дуге

Для того, чтобы найти радиус R криволинейного пути, рассмотрим период движения dt , в течении которого робот движется вдоль дуги окружности, имеющей угол Л9 .

-Левое колесо:

W пройденное расстояние = VLdt; радиус дуги = R - —

-Правое колесо:

W пройденное расстояние = VRdt; радиус дуги = R + —

• -Обе колесные дуги имеют в основании один и тот же угол Л9 :

• V, A t    V_R A t    W

Ав = L ™_r = R „л ^ — ( V_L + Vr ) = R^Vr - V ) ^

WW2LR  RL r — r +-- 22

^ R = W ( V L + V R )

2 ( V r - V l )

( V_R - V )A t Ав = (-^ L^—

W

2)Реечно-зубчатый привод

Такой тип роботов имеет два мотора - один для движения, другой для руления [3].

• - Не может нормально развернуться на месте.

• - При постоянной скорости и угле поворота движется по дуге окружности.

• - В четырехколесной схеме необходим задний дифференциал и переменная связь («Принцип Аккермана») на рулевые колеса (рис. 3).

  

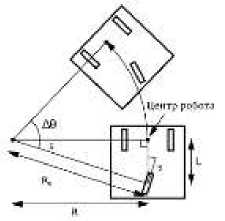
  Рис. 3. Круговое движение трехколесного робота

  
  

При условии, что отсутствует боковая пробуксовка колес, пересечем оси передних и задних колес, чтобы сформировать прямоугольный треугольник, и в результате получим:

R =

L tg (s)

Радиус траектории, которую описывают задние колеса:

R

d

L sin( s)

За время ^t расстояние вдоль этой дуги окружности, пройденное приводными колесами равно vAt , поэтому угол Л9 на который повернется робот:

_д<9_ V A t _ V A t sin( s )

R d

L

R = — tg(s )

3)Зубчатые передачи

Двигатели постоянного тока, как правило, обладают высокой скоростью вращения и низким крутящим момент, поэтому зубчатая передача практически всегда необходима для управления роботом (рис. 4).

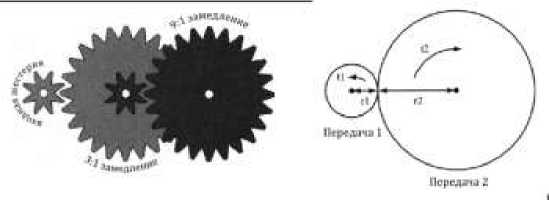
Рис. 4. Передачи

Если Передача 1 имеет крутящий момент  й,  она оказывает тангенциальную силу F = — на Передачу 2. r1

Крутящий момент Передачи 2 поэтому t2 = r2F = r2 tv r1

Изменение угловой скорости между Передачей 1 и Передачей 2

вычислим, рассмотрев скорость в точке где они соприкасаются [4]:

-Когда маленькая шестерня приводит в движение большую, второе зубчатое колесо будет иметь более высокий крутящий момент и меньшую угловую скорость пропорционально соотношению зубьев.

-Для достижения комбинированного воздействия шестерни можно объединять в цепочки.

r

V = wxrx = wr ^ w2 = 1 Wj r2