Математическое моделирование адиабатического периода индукции для метан-кислородных смесей в широком диапазоне начальных давлений и температур

Оценка величины адиабатического периода индукции tad (часто называемого временем задержки воспламенения) для реагирующих смесей произвольного состава, при заданной начальной температуре и давлении необходима, для оценки пожаро-взрывобезопасности веществ и технологических процессов, а. так же для современных методов анализа, и числен ного моделирования детонационных волн.

Моделируемая система, представляет собой замкнутую идеально теплоизолированную емкость постоянного объема, в начальном состоянии заполненнуто смесью газообразных веществ, способных вступать в систему суммарно-экзотермических реакций. Состав смеси, ее начальная температура, и давление задаются. В такой системе при любых начальных усло виях выделяющееся в ходе реакций тепло приводит к прогрессирующему разогреву смеси, заканчивающемуся тепловым взрывом через tad. Длительность периода индукции зависит как от начальных условий и теплофизических свойств среды, так и от параметров химической реакции (константы скорости, энергии активации, теплового эффекта). В ходе процесса.

меняется химический состав реагирующей смеси и ее температура.

Задача, об адиабатическом тепловом взрыве впервые была, решена. О.М. Тодесом в 1933 г.

[1]. В пределе простой одностадийной сильно экзотермической реакции выражение для оцен

ки tad выглядит так [2]

tad =

cρ RT ₀ ²

Qz 0 E

E _e RT 0

Здесь с, р - теплоемкость и плотность реагирующей смеси; R- универсальная газовая постоянная; T 0 - начальная температура реагирующей смеси; Q,E - тепловой эффект и энергия активации реакции; z о - т.н. предэкспонент, имеющий размерность обратную времени и зависящий от начальной концентрации реагентов и порядка, реакции [2, 3].

Применение этой простой формулы весьма ограничено, поскольку большинство процессов горения и взрыва (в частности - в газовой фазе) имеют сложные кинетические механизмы разветвленных цепных реакций. Они включают в себя комплексы из десятков, сотен и даже тысяч химических реакций ( nr ) с участием десятков-сотен реагентов ( nc ), демонстрируют кинетическое поведение, принципиально отличающееся от поведения простых реакций [4] и, чаще всего, не могут быть описаны единой простой брутто-реакцией, пригодной для моделирования процесса горения в широком диапазоне изменения концентраций и температур. Для математического моделирования цепных реакций приходится численно решать системы из nc обыкновенных дифференциальных уравнений химической кинетики, обладающие высокой степенью математической жесткости [5, 6]. Аналитические решения здесь невозможны, и численное моделирование является единственно возможным инструментом для исследования подобных задач.

1.    Постановка задачи

Объект моделирования - изохорный адиабатический реактор представляет собой замкнутую, идеально теплоизолированную емкость постоянного объема V, в которой находится химически реагирующая смесь переменного состава из nc газообразных компонентов — исходных веществ, промежуточных и конечных продуктов реакций, а так же инертных веществ в реакциях не участвующих. В таком реакторе могут одновременно протекать nr элементарных химических реакций, механизм и кинетические константы для которых известны.

В начальный момент времени t = 0 задаются: начальная температура T о, давление P 0; состав смеси задается набором начальных мольных долей компонентов:

где

Xi =

Ci

Е с i

Ni

Е N i

i = 1 ... nc,

Ci, Ni - мольная коицеитрация CC= = -p i^

и количество молей г-го компонента сме

си. Обозначим как Cs = ^^ Ci - суммарную концентрацию и Ns = ^^ Ni - суммар- ii

ное

количество молей в смеси. Соответственно начальные значения будем обозначать как

x 0 i ,C 0 i ,N 0 i ,C 0 S ,N 0 S

Важным допущением является отсутствие начальных градиентов концентраций, температуры и давления в объеме реактора - т.е. в начальный момент во всех точках реактора они одинаковы. Поскольку система идеально изолирована, на стенках реактора градиенты концентраций, температуры и давления равны нулю. Следствием этого является отсутствие градиентов на протяжении всего процесса - концентрации, температура и давление будут меняться синхронно во всех точках реагирующей смеси. Математическая модель реактора может быть описана системой обыкновенных дифференциальных уравнений с начальными условиями, в которой единственной независимой переменной будет время t.

2.    Вывод основных соотношений для идеального газа

Используем общепринятые принципы построения моделей макрокинетики и химической газодинамики [2-5].

• а)    Уравнение баланса массы. В замкнутой системе постоянного объема масса m и

• плотность р вещества не меняются

m = У? mi = У? m о i = m о^; Р = УУ Pi = УУ Р ⁰ i = Р о^; Р = m ’ i = 1 -"Пс-    ^

ii

ii

При этом, массы отдельных компонентов mi и их плотности pi могут меняться во времени из-за протекания химических реакций, но соотношения (3) должны выполняться. Добавим еще несколько соотношений, связывающих массы и плотности с концентрациями

Pi = р,А ; р = ^ ^iCi ;   m = V^^Ci,                 (4)

ii где p, - молярная масса г-го компонента смеси.

Начальные масса и плотность смеси определяются по начальным мольным долям, температуре и давлению с помощью уравнений состояния. Подробнее этот момент будет обсуждаться ниже.

• б)    Уравнение баланса массы г-го компонента смеси. Как уже отмечалось выше, массы отдельных компонентов mi могут меняться во времени из-за протекания химических превращений. В замкнутом безградиентном реакторе это единственный фактор, влияющий на баланс массы, поэтому скорость изменения mi может быть получена из соотношения

nr dmi

= Afij, j =1

гДе rij ~ скорость производства или расходования массы г-го компонента в j-й реакции. Запишем фю реакцию в виде обобщенного стехиометрического уравнения v 1 ,jA1 + v2,jA2 + . . . + vnc,jAnc ^ V1 jA1 + v2jA2 + . . . + vnc,jAnc             (6)

Здесь Ai - химический символ г-го реагента (например H2 , CO2 , CH4 , CH2O и т.д.); vi.j, vij - стехиометрические коэффициенты г-го вещества в j-a реакции, которые показывают сколь

ко молей (или молекул) данного реагента вступают в реакцию как исходные вещества ( vij )

или получаются как продукты реакции не участвующих в j-a реакции равны 0.

(vi.j)

. Стехиометрические коэффициенты

веществ,

Скорость j-a газофазной реакции определяется законом действующих масс (зависимость от концентраций) и законом Аррениуса (зависимость от температуры) [2, 3] и может быть выражена как

Wj = Zj Tbj exp ( - RET )ft C"^u.                        17)

i =1

Здесь Zj,bj,Ej - кинетические константы для расчета скорости фй реакции.

Скорость производства и расходования массы г-го компонента в j-a реакции выражается как rij — Wj (Vij   Vi j) EiV,

а скорость изменения массы г-го вещества во всем комплексе реакций получается суммированием вкладов каждой реакции в производство или потребление данного вещества nr dmi

= № V У2 Wj ^Vvj,j ~ ^vi,j) .

j =1

С учетом (4) данное выражение можно записать в более удобном для практического применения виде dC    nr

j =1

• в)    Уравнение баланса энергии. Поскольку энергетический обмен реактора с окружающей средой запрещен, суммарная энергия рассматриваемой системы не меняется, что может быть сформулировано в виде постоянства суммарной энтальпии. Но обмен энергией между компонентами системы происходит непрерывно, в частности в экзотермических химических реакциях химическая энергия переходит в тепловую, в эндотермических - наоборот.

Уравнение баланса энергии запишем как nc

Cihi = const ,                                       (11)

i =1

здесь hi - удельная мольная энтальпия г-го вещества). Уравнение сохранения энергии удобнее записать в дифференциальной форме d nc        nc dh dC dt^Cihi = Е (Ci+ hi=0.

i =1          i =1

В этом выражении dCi/dt определено выше зависимостью (10), а производную энтальпии преобразуем как dhi   dhi dT dT dt    dT dt     pi dt 1

здесь cpi - изобарная молярная теплоемкость г-го вещества; (12) принимает вид

^£ ( Cicp-" + hiC ) =0 .

tt i=1

В случае идеального газа энтальпия и теплоемкость зависят только от температуры и из (13) получаем уравнение для контроля текущей температуры газовой смеси.

-

dT dt

£ |-.'-Д| i=1

nc

Е [ CiCpi ( T )] i =1

При высоких давлениях необходимо применять уравнение состояния реального газа, а энтальпия и теплоемкость будут зависеть и от давления. Особенности построения энергии для этого случая будут обсуждаться ниже.

Зависимости hi ( T ) и cpi ( T )для всех веществ задаются в виде термодинамических полиномов. Зависимости для hi ( T ) получены аппроксимацией табличных зависимостей энтальпии из [7] полиномами 3-го порядка, работающими в диапазоне температур от 300 до 4000 К. Зависимости для Cpi ( T ) получены дифференцированием по температуре полиномов для энтальпии.

• г)    Задание начальных концентраций. Для решения поставленной задачи - определения периода индукции данная система должна быть дополнена начальными условиями, задающими начальные концентрации и температуру

t = 0 , T = T 0 ,   Ci = C 0 i.

В предыдущем разделе было отмечено, что начальное состояние реактора определяется иначе - задается начальная температура, давление и мольные доли реагентов (2). Переход от этой системы данных к (15) возможен с использованием уравнения сохранения массы (4) и применяемого уравнения состояния газовой смеси.

В случае идеального газа из уравнения состояния

P о =     RT о = C о s RT о

выражаем начальную суммарную концентрацию

C о s =

P 0

RT 0

и начальные концентрации всех компонентов

C о i — xi^C о S ,    i — 1 . . . nc.

Таким образом, мы можем решить сформулированную выше задачу численно. Математическая модель адиабатического реактора описывается уравнением баланса энергии (14) для определения температуры реагирующей смеси Т и nc уравнениями (10) для мольных концентраций каждого из реагентов. На каждом шаге решения мы получаем вектор текущих концентраций Ci и текущую температуру T. При необходимости, текущее давление можно рассчитать по формуле (16)

p — rt ^ Ci

i =1

• д)    Определение периода индукции. Для определения tad используется общеприня

  тый в теории теплового взрыва критерий -/ дт \

  выделения ( max -7^- I.

  
  

  момент достижения максимума скорости тепло-

  
  
3.    Выбор уравнения состояния реального газа

Для корректного описания процессов в газовой фазе при высоких давлениях необходимо применять уравнение состояния, учитывающее силы взаимодействия молекул при их сближении, в частности силы отталкивания. Уравнение должно отвечать следующим требованиям:

• а)    Уравнение должно быть работоспособным при очень высоких давлениях - как минимум до 2000 МПа.

• б)    Структура этого уравнения должна позволять ему гибко приспосабливаться к сложной смеси газов переменного состава, что важно при описании химически реагирующей среды.

• в)    Это же уравнение должно быть пригодно и для отдельного описания любого индивидуального компонента смеси.

Исходя из этих требований, из многообразия уравнений состояния, применяемых для описания реального газа [8, 9], для дальнейшего применения было выбрано уравнение Беккера - Кистяковсого - Вильсона (общепринятое сокращение BKW), [10]

PVm RT

— 1 +

χK

( т + е ) ^а

βχK e ( T + в)^а

Здесь Vm - молярный объем газовой смеси (величина обратная суммарной концентрации Cs\, коэффициент K для рассмотренной выше смеси реагентов определяется выражением nc

K =         ,                                   (21)

i =1

где ki - т.н. коволюмы индивидуальных компонентов смеси; Ci - их концентрации.

Как показано в [8, 10] существует несколько методик определения значений коволтомов (геометрический, через потенциал Леннарда - Джонса, экспериментальный). В [10] приведена таблица, значений коволтомов, определенных разными методами - разброс величин для одного вещества, достигает десятков процентов. В дальнейших расчетах использовались значения, приведенные в табл. 1. Большая часть значений взята, из [10], предпочтение отдавалось экспериментально определенным значениям, при отсутствии таковых брались наименее противоречивые значения, определенные по потенциалу Леннарда. - Джонса, или геометрические коволюмы. Для ряда, веществ данные отсутствуют, и значения коволюмов были рассчитаны самостоятельно по геометрической методике, описанной в [10].

Таблица 1

Коволюмы индивидуальных веществ ki, с м³/моль

В-во	ki	В-во	ki	В-во	ki	В-во	ki
H2	120	CH4	400	H2O2	590	C2H3	1150
O2	300	C2H6	1100	CH	472	C2H4	1100
N2	380	H	60	CH2	520	C2H5	1100
H2O	250	O	120	CH3	520	CHO	860
CO	380	OH	410	C2H	950	CH2O	815
CO2	600	HO2	590	C2H2	1013	CH3O	860

Эмпирические параметры а, в, X, 9 подбираются по экспериментальным данным, в частности по адиабатам Гюгонио для продуктов детонации. В [10] приведена, таблица, рекомендуемых параметров уравнения BKW для продуктов детонации различных взрывчатых веществ. Все эти наборы параметров, а. также некоторые другие, встречающиеся в литературе по детонации, были протестированы на. задаче моделирования зависимости молярных объемов отдельных газов от давления и температуры (см. ниже). Сравнение полученных зависимостей с экспериментальными данными из книги Циклиса [11] показало, что наиболее удовлетворительный результат дал единственный набор параметров а = 0 , 25, в = 0 , 3, X = 1, 9 = 0, рекомендованный Хэллфордом [8].

Уравнение состояния в этом случае принимает более простой вид

PVm RT

K     0 , 3 ·K

= ^{1 +} ^ 0 ) 25 e T0, ²⁵ •

Это уравнение, называемое так же уравнением Хэлфорда. - Кистяковсого - Вильсона, рекомендовано в [8] для решения задач детонации при давлениях до 20 000 МПа.

Данные соображения и привели к однозначному выбору уравнения (22) в качестве объекта. моделирования.

Оценка работоспособности уравнения проводилась по следующей методике. Если записать уравнение (22) не для смеси газов, а. для объема, заполненного чистым веществом г-го сорта, мы получим уравнение состояния индивидуального газа.

PVmi RT

0 , 3 C k                                    ^{0 , 3 k}i

^Ciki   T 0 , 2 ⁱ 5 ^{i               ki}       VmiT 0 , 25

^{1 +} T ⁰ ,25 e             VmiT ⁰ ,25

.

Его можно преобразовать к виду стандартного алгебраического уравнения, трансцендентного относительно мольного объема Vmi.

PVmi RT

- 1 -

ki _VmiT 0 , 25

0 , 3 k_{i e} V_miT 0 , 25

= 0 .

Численно решая это уравнение при различных сочетаниях Р и Т можно получить таблицу функции Vmi = f ( P,T,ki ) и сравнить полученные результаты с экспериментальными данными, приводимыми в литературе. Так в [11] приведен набор экспериментальных зависимостей мольных объемов для ряда газов. Для решаемой ниже задачи моделирования горения метан - воздушной смеси есть данные только для пяти компонентов - N2 , H2 , O2 , CO2 , CH4 . Решение уравнения (24) производилось с помощью встроенной в пакет Mathcad функции root и с помощью программного модуля, реализующего быстро сходящийся метод секущих-хорд, который далее был использован в основной Фортран - программе.

Для водорода рачетные данные хорошо согласуются с литературными данными; в остальных случаях уравнение (24) дает несколько завышенные значения мольных объемов, причем с повышением давления расхождение данных уменьшается.

4.    Особенности модели адиабатического реактора в случае реального газа 4.1.    Расчет начального состава смеси в реакторе с помощью уравнения состояния реального газа

Вернемся к задаче расчета начальных концентраций при заданном давлении P 0, температуре T 0 и составе смеси в виде мольных долей реагентов x 0 i. Порядок расчета таков.

• а)    Рассчитываем мольные объемы Vmi для всех компонентев смеси, для которых x 0 i = 0, решая трансцендентное уравнение (24) при P 0 , T 0 .

• б)    Далее руководствуемся следующими соображениями. Если общее (заранее неизвестное) количество молей N 0 s поместить в реактор объемом V, то количество молей г-го вещества будет равно N 0 i = x 0 iN 0 s . С другой стороны, это количество молей будет при заданных условиях занимать объем V = N 0 iVmi, а сумма этих объемов должна быть равна объему реактора

nc              nc                        nc

V = 52 N ° iVmi = 52 X ° iN 0 S Vmi = N 0 S    ⁰ iVmi'

i =1             i =1                       i =1

Поделив правую и левую часть этого соотношения на V, имеем

nc

C 0 S    x 0 iVmi

= 1 ,

i =1

что при уже известных мольных объемах дает выражение для расчета суммарной концентрации

C 0 S =

nc x0iVmi i=1

• в)    Определяем начальные концентрации всех компонентов C 0 i = XiC 0 s ; i = 1 .. .nc

Очевидно, что из-за худшей сжимаемости реального газа, при росте давления эти концентрации будут меньше, чем при том же давлении и температуре в идеальном газе. Это должно привести, в соответствии с формулой (7), к замедлению реакций и увеличению периода индукции, причем этот эффект будет усиливаться с ростом давления.

Если по ходу решения необходимо рассчитывать текущее давление для вычисления поправок к энтальпии и теплоемкости, то для этого используется уравнение (22)

P = CS RT (1 + K e 0 • ³ TK⁵ ) ;

nc

K = ^№.

i =1

• 4.2.    Влияние давления на энтальпию и теплоемкость реального газа

Как показано в [12], уравнение, выражающее зависимость энтальпии от давления при постоянной температуре выглядит следующим образом

Разделяя переменные и интегрируя (27) от P о до P получаем выражение для изменения энтальпии за счет роста давления (в нашем случае P о = 0 , 1 МПа)

P

H ( P,T ) - H ( Pо ,T ) = Г

P 0

P 0

V-

^{T   ∂} ∂ ^V T  P

dP.

Переписав это соотношение для парциальных мольных энтальпий, получаем

A hi ( P,T ) = hi ( P,T ) - hi ( P о ,T )

= l: v

-T

∂_∂V_Tmi _P

dP ;

i = 1 ... nc.

Здесь, как и раньше, V_mi - мольный объем г-го вещества. Поскольку Vmi определяется решением трансцендентного уравнения (24), аналитическое вычисление интеграла и производной в правой части (29) невозможно. Их можно вычислить с помощью численных методов. При отработке методики с помощью математического пакета Mathcad были использованы встроенные функции численного дифференцирования и интегрирования.

Полученные по (29) значения оказались выше, чем литературные оценки [11], полученные с помощью аналогичного уравнения, но с использованием уравнения состояния Тэйта и методов графического дифференцирования. При этом общий характер зависимостей практически одинаков.

Поправку к теплоемкости г-го вещества за счет высокого давления можно получить путем численного дифференцирования выражения (29) по температуре

А (РТХ- д A hi ( P,T ).    .  ,

^A cpi ^{( P}, ^T ) —      dT ’ i — ¹ ... nc^.                         (A))

Существенным недостатком численного расчета поправок (29), (30) является необходимость многократного расчета мольных объемов Vmi, которые в свою очередь, получаются итерационным решением трансцендентного уравнения (24). Поэтому применение высокоточных встроенных методов численного дифференцирования и интегрирования приводит к неоправданно большому времени расчета, которое ощутимо даже на высокопроизводительных компьютерах. С целью снижения вычислительных затрат было произведено исследование возможности применения простых вычислительных схем меньшей точности, но требующих минимума вычислений. После серии численных экспериментов выбор был остановлен на следующих методах.

• а)    Для вычисления производных в формулах (29), (30) с сохранением минимум 6 верных значащих цифр хорошо подходит центрально-разностная формула 2-го порядка точности при вариации температуры на 0 , 1 K.

• б)    Для численного вычисления интеграла в (29) оптимальным оказалось применение метода наивысшей алгебраической точности Гаусса с 8 узлами, обеспечивающего при минимуме вычислений 4-5 точных значащих цифр, что для данной задачи вполне достаточно.

• 4.3.    Модификация уравнения баланса энергии

Именно эти методы и были применены в основной Фортран-программе.

Для случая реального газа уравнения (10) остаются без изменения, а вывод уравнения баланса энергии должен быть пересмотрен. В формуле (12) появляются дополнительные слагаемые, учитывающие влияние давления. Производную энтальпии преобразуем так dhi   dhi dT   dhi dP dT   dhi  dP dT   dP dCi

dt    dT dt   dP dt    pi dt   dP  dT dt   dCi dt

Уравнение энергии принимает вид nc           dhi dP dT

Ц Г (^Cpi ⁺ №dT) It ⁺ V ⁺ Ci

dhi dP dP dCi

)■ и *

В случае реального газа уравнение для контроля текущей температуры газовой смеси будет выглядеть так

dT dt

- Е[(м T ) + a hi ( p,t ) + Ci^dA;dl) . dC]

i 1 ⁱ

E Ci L ( T ) + A cpi ( P,T ) + dl Ц

Аналитические выражения для расчета производных давления по температуре и кон центрации получаются дифференцированием (26)

= CSR{1 + Ke03TK5 [1 -0•25 (1 + T0K)]};   K = ЕCiki.^

Значение для производной энтальпии по давлению рассчитываем численно в соответствии с приведенным выше выражением (27)

(dl) т - - - (1mi),-

5.    Реализация основного вычислительного алгоритма

Для решения всех задач, описанных ниже, использована система программирования Compaq Digital Visual FORTRAN v. 6.6. При программировании модулей для расчета правых частей уравнений химической кинетики и матрицы Якоби использовалась технология прямых безиндексных вычислений, что существенно повышает скорость вычислений. Исходные тексты соответствующих модулей на ФОРТРАНЕ генерируются автоматически с помощью специально разработанной программы.

Решение жесткой системы дифференциальных уравнений выполнялось с использованием солвера STIFF, основанного на многошаговом методе Гира переменного порядка, специально адаптированного для решения задач химической кинетики [6]. Он имеет весьма эффективный блок адаптивного выбора шага. Позволяет использовать для вычисления матрицы Якоби внешнюю пользовательскую процедуру, хотя имеет и встроенные средства для ее численного расчета. Длительный опыт применения данной программы показал высокую эффективность и устойчивость при решении широкого круга задач теории горения.

Для расчетов использовалась широко известная и многократно апробированная кинетическая схема окисления легких углеводородов, предложенная в [13]. Использован несколько укороченный вариант (первые 78 обратимых реакций). Исключены ненужные для решаемой задачи реакции окисления метанола. Поскольку обратимую реакцию удобно рассматривать как две независимые односторонние реакции, принятая схема включает 156 реакций, 23 активных реагента. (H 2. O 2. H 2 O. CO. CO 2. CH 4. С 2Щ. H. O. OH. HO 2. H 2 O 2. CH. CH 2. CH 3. C 2 H. C 2 H 2. C 2 H 3. C 2 H 4. C 2 H 5. CHO. CH 2 O. CH 3O) II одни ииерт N 2.

Таким образом, решается система, из 25 дифференциальных уравнений (24 концентрации + температура), nc = 24; nr = 156 .

Для решения задачи расчета, адиабатического периода, индукции применялись 3 модификации программы:

Вариант 1 реализует модель процессов в идеальном газе на. основе уравнений (10), (14);

Вариант 2 реализует модель процессов в реальном газе на. основе уравнений (10), (33);

Вариант 3 реализует комбинированную модель процессов в газе на. основе уравнений идеального газа. (10), (14), но с учетом начального сжатия в соответствии с уравнением (25) для реального газа; влияние давления на. энтальпию и теплоемкость не учитывается.

В связи с тем, что что варианты 1 и 3 программы фактически отличаются только способом определения начального состава, быстродействие этих программ почти не отличается. Вариант 2 программы, напротив, при каждом обращении к модулю расчета, правых частей дифференциальных уравнений, выполняет массу дополнительных операций, связанных с расчетом текущего давления; поправок на. давление к энтальпиям 24 веществ; численным интегрированием и дифференцированием; расчетом поправок в уравнении энергии. При этом приходится многократно перевычислять мольный объем каждого компонента, смеси итерационным решением трансцендентного уравнения (24). В результате, этот вариант программы решает задачу на. порядок медленнее остальных.

6.    Результаты расчетов

Рассчитываются адиабатические периоды индукции для разных составов метанкислородных и метан-воздушных смесей при заданном начальном давлении. Расчеты проводились для следующих начальных давлений: 0,1, 1, 10, 100, 1000 МПа. При заданном давлении, расчеты проводятся одним потоком последовательно для серии начальных температур от 800 до 2500 К через 100 К.

• а)    Сравнение периодов индукции в идеальном и реальном газе для стехиометрической метан-кислородной смеси (2O 2 + CH 4)

Использовались варианты 1 и 2 программ. Результаты расчетов приведены на. рис. 1 и, выборочно, в табл. 2. Хорошо видно, что при низких давлениях периоды индукции в идеальном и реальном газах отличаются незначительно. Однако, начиная с давления 10 МПа, разница становится достаточно ощутимой. Начиная с 100 МПа, она видна даже на графиках в логарифмических координатах. Для давлений порядка 1000 МПа период индукции в реальном газе в несколько раз больше, чем в идеальном. При росте начальной температуры относительная разница в периодах индукции идеального и реального газов уменьшается.

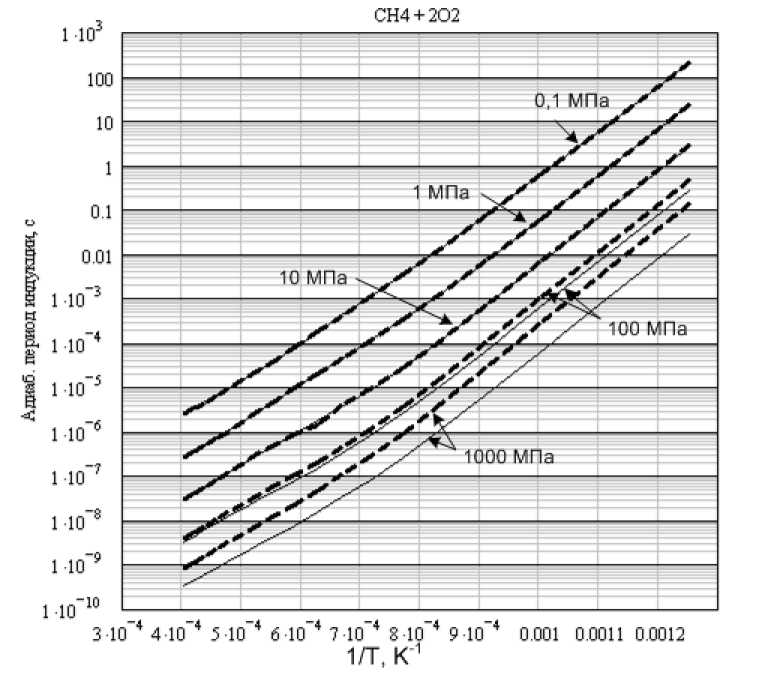
Рис. 1. Стехиометрическая метан-кислородная смесь. Сравнение результатов расчетов для идеального (сплошная линия) и реального газов (пунктир)

• б)    Сравнение периодов индукции в идеальном и реальном газе для стехиометрической метан — воздушной смеси (2O2 + CH4 + 7 , 52N2)

Расчеты проводились для тех же начальных давлений теми же вариантами программы. Результаты расчетов приведены на рис. 2 и, выборочно, в табл. 3. Здесь тенденция та же самая - при низких давлениях периоды индукции отличаются незначительно, а начиная с с давления 10 МПа, разница, в периодах индукции в идеальном и реальном газах становится достаточно ощутимой. При этом относительная разница, при одинаковой температуре несколько больше, чем в случае метан-кислородной смеси. При росте начальной температуры относительная разница, в периодах индукции идеального и реального газов также уменьшается.

• в)    Сравнение периодов индукции в двух моделях реального газа для стехиометрической метан — кислородной смеси (2O2 + CH4) и стехиометрической метан — воздушной смеси (2O2 + CH4 + 7 , 52N2)

С целью выделения доминирующих факторов, влияющих на. период индукции в реальном газе, была, выполнена, серия аналогичных расчетов вариантом 3 программы, которая

Таблица 2

Результаты расчета периода индукции, с для смеси 2O2 + CH4

р, МПа	Модель газа	Температура, К
		800	900	1000	1200	1500	2000	2500
	Идеальный	202,0	7,945	0,577	0,013	4,00е-4	1,42е-5	2,39е-6
ОД	Реальный	202,2	7,951	0,577	0,013	3,87е-4	1,42е-5	2,39е-6
	Комбин.	202,2	7,952	0,577	0,013	4,00е-4	1,42е-5	2,39е-6
	Идеальный	22,17	0,819	0,056	1,20е-3	4,28е-5	1,66е-6	2,47е-7
1	Реальный	22,38	0,830	0,057	1,21е-3	4,ЗЗе-5	1,67е-6	2,48е-7
	Комбин.	22,37	0,826	0,057	1,21е-3	4,30е-5	1,67е-6	2,48е-7
	Идеальный	2,50	0,089	5,86е-3	1,08е-4	3,60е-6	1,85е-7	2,74е-8
10	Реальный	2,72	0,097	6,28е-3	1,09е-4	3,73е-6	1,91е-7	2,80е-8
	Комбин.	2,71	0,095	6,25е-3	1,14е-4	3,77е-6	1,91е-7	2,80е-8
	Идеальный	0,2659	9,254е-3	6,03е-4	1,08е-5	3,23е-7	1,77е-8	3,12е-9
100	Реальный	0,4478	0,0151	9,47е-4	1,59е-5	4,45е-7	2,28е-8	3,78е-9
	Комбин.	0,4413	0,0147	9,26е-4	1,56е-5	4,40е-7	2,25е-8	3,72е-9
	Идеальный	0,0271	9,43е-4	6,11е-5	1,08е-6	3,20е-8	1,75е-9	3,27е-10
1000	Реальный	0,1312	4,255е-3	2,60е-4	4,09е-6	1,04е-7	4,79е-9	7,63е-10
	Комбин.	0,1264	4,050е-3	2,46е-4	3,87е-6	1,00е-7	4,61е-9	7,ЗЗе-10

Таблица 3

Результаты расчета периода индукции, с для смеси 2O2 + CH4 + 7 , 52N2

Р, МПа	Модель газа	Температура, К
		800	900	1000	1200	1500	2000	2500
	Идеальный	831,1	34,80	2,722	0,068	1,78е-3	5,30е-5	8,54е-6
ОД	Реальный	832,0	34,84	2,724	0,068	1,79е-3	5,30е-5	8,54е-6
	Комбин.	832,0	34,84	2,724	0,068	1,79е-3	5,30е-5	8,55е-6
	Идеальный	88,18	3,482	0,258	6,61е-3	2,35е-4	6,65е-6	9,13е-7
1	Реальный	89,07	3,511	0,260	6,65е-3	2,36е-4	6,69е-6	9,22е-7
	Комбин.	89,06	3,514	0,260	6,65е-3	2,36е-4	6,67е-6	9,15е-7
	Идеальный	10,07	0,376	0,026	5,43е-4	2,12е-5	9,11е-7	1,11е-7
10	Реальный	11,03	0,410	0,028	5,52е-4	2,24е-5	9,40е-7	1,14е-7
	Комбин.	11,01	0,407	0,028	5,77е-4	2,23е-5	9,36е-7	1,13е-7
	Идеальный	1,099	0,040	2,69е-3	5,12е-5	1,64е-6	1,05е-7	1,58е-8
100	Реальный	1,891	0,066	4,31е-3	7,80е-5	2,38е-6	1,39е-7	1,92е-8
	Комбин.	1,872	0,065	4,24е-3	7,60е-5	2,38е-6	1,ЗЗе-7	1,87е-8
	Идеальный	0,113	4,11е-3	2,73е-4	5,12е-6	1,56е-7	8,31е-9	1,72е-9
1000	Реальный	0,571	1,95е-2	1,23е-3	2,10е-5	5,73е-7	2,52е-8	4,64е-9
	Комбин.	0,554	1,85е-2	1,16е-3	1,93е-5	5,16е-7	2,83е-8	4,37е-9

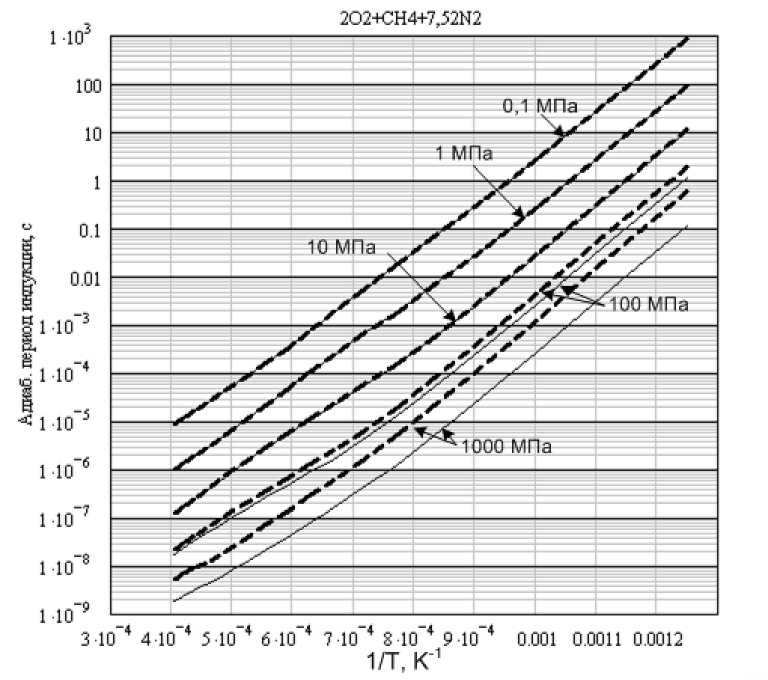
Рис. 2. Стехиометрическая метан - воздушная смесь. Сравнение результатов расчетов для идеального (сплошная линия) и реального газов (пунктир)

фактически является моделью идеального газа, за исключением того, что начальные концентрации ораделяются на основе уравнения реального газа. В таблицах 2 и 3 показаны результаты сравнения этой серии расчетов (в графе « комбинированная модель » ) с зависимостями, полученными в пунктах а) и б). Результат оказался довольно неожиданным - из таблиц ясно, что максимальные расхождения результатов, полученных вариантами 2 и 3 программы, не превышают нескольких процентов, да и то только при высоких давлениях.

7.    Анализ полученных результатов

• а)    Очень слабое влияние довольно больших по величине поправок к энтальпии и теплоемкости, показанное в предыдущем разделе, на первый взгляд выглядит весьма неожиданным. Именно энтальпии определяют тепловые эффекты реакций, и их изменение, казалось бы, должно приводить к изменению температуры в соответствии с уравнениями (14), (33). Температура же очень сильно влияет на скорость реакции в соответствии с законом Аррениуса (7), что может вызвать изменение периода индукции. Объяснить наблюдаемое отсутствие такого сильного эффекта можно тем, что тепловой эффект реакции определяется, в соответствии с законом Гесса [3], разностью энтальпий продуктов реакции и ее исходных веществ. В случае, если при изменении давления энтальпии веществ меняются синхронно, разность энтальпий будет сохраняться.

Однако вопрос о синхронности изменения энтальпий остается открытым. В соответствии с формулой (29) поправка на давление рассчитывается через мольные объемы компонентов, а они все же меняются по-разному, т.к. у реагентов коволюмы отличаются по величине. Детальное исследование промежуточных результатов вычислений показало, что дополнительные слагаемые в числителе и знаменателе правой части уравнения (33) имеют тот же порядок, что и основные слагаемые в уравнении (14). Однако, определяющие скорость изменения температуры соотношения числителя и знаменателя, вычисляемые по формулам (14) и (33) сохраняют близкие по величине значения в ходе всего периода индукции. Поправки взаимно компенсируют друг друга.

Этот эффект дает весьма полезный результат. Если нас устраивает определение периода индукции с ошибкой в несколько процентов, да и то только при очень высоких давлениях, моснсно в расчетах не вычислять очень трудоемкие поправки на давление для термодинамических параметров.

• б)    В свете сказанного выше, легко выделить доминирующий фактор, определяющий влияние давления на период индукции. Это начальное сжатие реагирующее смеси.

Запишем уравнение состояния в обобщенном виде

PV

NRT = ( 0, 0), где Z - коэффициент сжимаемости. Для идеального газа Z = 1, а для реального газа при высоком давлении Z > 1.

Выразим начальную суммарную концентрацию при заданных P ° , T °

P 0

C = N ° S ___________

⁰ S V     Z ( P ° , T ° ) RT° ■

Отсюда становится понятно, что начальная концентрация в идеальном газе (при прочих равных условиях) всегда будет больше, чем в реальном газе при высоком давлении, причем с повышением давления эта разница будет возрастать. Увеличение температуры несколько уменьшает Z (см., например, уравнение (22)) и повышает начальную концентрацию.

Уменьшение начальной концентрации в реальном газе, рассчитанной по формуле (25), эквивалентной (37), приведет к пропорциональному уменьшению концентраций промежуточных продуктов и, в соответствии с законом действующих масс, к замедлению скорости всех реакций. В следствие этого период индукции увеличивается. Именно это и определяет все особенности поведения периодов индукции в реальном и идеальном газе, отмеченные в предыдущем разделе, в том числе и уменьшение относительного отклонения периодов индукции с ростом температуры.

• в)    Не следует забывать, что рассматриваемая модель адиабатического реактора является весьма идеализированной. При низких начальных температурах и давлениях периоды индукции составляют сотни и тысячи секунд, и обеспечить на практике действительную адиабатичность реактора можно только с некоторой степенью приближенности.

Напротив, при высоких температурах и давлениях периоды индукции, становятся чрезвычайно малыми. На практике такие начальные условия создаются ударным сжатием газа, которое выполняется не мгновенно. Если период индукции становится соизмерим с временем сжатия, или даже становится меньше его, данная модель уже не будет работать, т.к. на ход реакций будет влиять скорость нарастания температуры и давления.

Работа проводилась при финансовой поддерэюке проекта 2012 066 - Г321 ЮУрГУ.