Математическое моделирование адиабатического теплового взрыва для реакции окисления водорода
Автор: Пигасов Егор Евгеньевич, Рябинин Валерий Константинович, Ковалев Юрий Михайлович
Рубрика: Краткие сообщения
Статья в выпуске: 3 т.6, 2013 года.
Бесплатный доступ
В данной работе представлены результаты математического моделирования адиабатического реактора, заполненного газовой смесью водорода с воздухом. Несмотря на то, что реакция окисления (горения) водорода очень широко используется в практических целях, и существует достаточно большое количество публикаций, разработка кинетических схем горения водорода является актуальной и в настоящее время. В работе были апробированы различные кинетические схемы горения водорода и было показано, что наиболее точное описание экспериментальных данных удается получить, используя полную кинетику окисления. Показано, что использование сокращенной кинетики окисления допустимо лишь для описания высокотемпературной асимптоты, а упрощение механизма до одной брутто-реакции пригодно только для приблизительных оценок.
Водород, химическая кинетика, горение и взрыв, период индукции
Короткий адрес: https://sciup.org/147159219
IDR: 147159219 | УДК: 544.45
Текст краткого сообщения Математическое моделирование адиабатического теплового взрыва для реакции окисления водорода
Несмотря на то, что реакции окисления (горения) очень широко используются в практических целях, и существует достаточно большое количество публикаций, разработка кинетических схем горения водорода является актуальной и в настоящее время.
На протяжении длительного времени водород рассматривается как эффективное рабочее тело для двигательных установок вследствие его исключительной химической активности в сочетании с воздухом и кислородом в качестве окислителя, а также благодаря отсутствию токсических продуктов сгорания. Имеется ряд прямых свидетельств использования чистого водорода в качестве горючего для прямоточных воздушно-реактивных двигателей (ПВРД) и для камер сгорания жидкостных ракетных двигателей (ЖРД). Весьма часто [1] можно встретить упоминание об использовании водорода, как присадки к углеводородным горючим, особенно применительно к процессам горения в двигателях внутреннего сгорания (ДВС) с искровым зажиганием и воспламенением от сжатия (дизельные моторы).
Столь широкое использование водорода как энергоносителя в сочетании с очевидными проблемами безопасности технических устройств, где предполагается применение или появление водорода, требует ясного представления об его взрывных характеристиках при горении в специально организованном процессе (как в камере сгорания) или при аварийной ситуации (как при тяжелой аварии с потерей охлаждающего компонента на АЭС). При рассмотрении рабочего процесса в ПВРД, ЖРД, ДВС следует заботиться о высокой эффективности и устойчивости преобразования горючей смеси в камерах сгорания (ПВРД, ЖРД, ДВС) и газогенераторах (ЖРД). Особое внимание здесь следует обращать на переходные режимы горения при изменении рабочих параметров. Дополнительные вопросы появляются в связи с проблемой использования в двигательных установках комбинированных типов горючего, представляющих собой смесь водорода с углеводородами [2].
Одним из основных параметров, характеризующих реагирующую смесь, является адиабатический период индукции , расчет которого и рассмотрен в данной работе для различных кинетических механизмов окисления водорода.
Постановка задачи
Рассмотрим адиабатический реактор [3] – реактор, в котором отсутствует всякий тепло-и массообмен с окружающей средой, следовательно все тепло, получаемое в ходе экзотермических реакций окисления идет на разогрев системы. В таком реакторе тепловой взрыв происходит при любых начальных условиях. Отрезок времени от начала процесса до момента резкого увеличения температуры носит название адиабатического периода индукции ( задержка воспламенения ).
Расчет адиабатического периода индукции сводится к решению системы обыкновенных дифференциальных уравнений для описания поведения температуры смеси и концентраций реагентов:
dT _ A -H(T) dt = k=l Cp(T)CkMk rm
£ Tbi k0i e -T Ц Cvij, i=1 j=1
r E m
— = £ V ij T b i • e i П C v ij , (2) i =1 j =1
где T – температура, t – время, r – число реакций, m – число реагентов, H – энтальпия, C p – теплоемкость, C – концентрация, M – молярная масса, E – энергия активации, k 0 , b – кинетические параметры, v ij – стехиометрический коэффициент для j -компоненты в i -реакции [1].
Теплоемкость C p и энтальпия H рассчитываются при помощи аппроксимации их зависимостей от температуры.
От использования тепловых эффектов реакций в явном виде при расчете температуры лучше отказаться вследствие их высокой температурной зависимости. В данной модели тепловой эффект учитывается в соответствии с законом Гесса, что делает модель более корректной.
При решении поставленной задачи необходимо решить систему дифференциальных уравнений, состоящую из одного уравнения (1) и m уравнений (2), где m – число реагентов. Стоит отметить, что, несмотря на кажущуюся простоту, данная система является весьма сложной для численного решения, поскольку в ходе процесса, описываемого данными уравнениями, скорости роста величин концентрации и температуры очень сильно изменяются, что делает систему не решаемой простыми явными методами ( коэффициент жесткости достигает 10 12 ).
Проблемы неустойчивости решения можно избежать, если использовать так называемые неявные методы решения. Другая возможность избежать этой проблемы – устранение быстрых стадий при помощи разделения временных масштабов [4].
Для решения данной системы уравнений разработана программа в среде MatLab, которая использует встроенный солвер ode15s, реализующий неявный метод Гира переменного порядка точности.
При расчетах использовались разные кинетические механизмы. Для простой модели весь процесс представлен одностадийной брутто-реакцией окисления молекулярного водорода:
2H 2 + O 2 = 2H 2 O.
Кинетические данные реакции: z o = 2,14 • 10 14 C ; E = 129000 Дж/моль [5].
Начальные концентрации H 2 - 0,6667, O 2 - 0,3333 (в мольных долях) при начальном давлении P = 1 атм.
Для более точной модели применяются более сложные кинетики (табл. 1).
В данном механизме реакции участвуют 6 компонентов:
H 2 , O 2 , H 2 O, H, O, OH.
Короткая кинетика окисления водорода [6]
Таблица 1
|
Схема реакции |
K + (моль,см,с) |
K - (моль,см,с) |
|
H+O 2 =OH+O O+H 2 =OH+H H 2 + OH = H + H 2 O OH+OH=O+H 2 O H 2 + M = H + H + M H 2 O + M = OH + H + M OH + M = O + H + M O 2 + M = O + O + M |
3x10 14 exp( - 8, 81/T) 3x10 14 exp( - 4, 03/T ) 3x10 14 exp( - 3, 02/T ) 3x10 14 exp( - 3, 02/T ) 1, 85x10 17 exp( - 54/T)/T 9, 66x10 18 exp( - 62, 2/T)/T 8x10 16 exp( - 52, 2/T )/T 5, 8x10 16 exp( - 60, 6/T)/T |
10 16 10 17 10 16 6x10 14 |
Здесь T – абсолютная температура, деленная на 1000.
Наиболее полная кинекика содержит 44 реакции – 22 прямых и 22 обратных (табл. 2).
Таблица 2
Полная кинетика окисления водорода [7]
|
№ |
Реакция |
Прямая реакция |
Обратная реакция |
||||
|
k 0 |
b |
E/R 0 |
k 0 |
b |
E/R 0 |
||
|
1,2 |
H + O 2 = OH + O |
2,2e7 |
0 |
2590 |
9,3e7 |
0 |
10250 |
|
3,4 |
O + H 2 = OH + H |
1,8e4 |
1 |
4480 |
8,3e3 |
1 |
3500 |
|
5,6 |
H + HO 2 = 2OH |
2,5e8 |
0 |
950 |
1,2e7 |
0 |
20200 |
|
7,8 |
2H + M = H 2 + M |
6,4e5 |
1 |
0 |
2,2e8 |
0 |
48300 |
|
9,10 |
H + OH + M = H 2 O + M |
1,4e11 |
2 |
0 |
2,2e10 |
0 |
52900 |
|
11,12 |
H + H 2 O 2 = HO 2 + H 2 |
6,3e6 |
0 |
550 |
6,8e7 |
0 |
9240 |
|
13,14 |
2OH + M = H 2 O 2 + M |
9,1e2 |
0 |
-2550 |
1,2e11 |
0 |
22900 |
|
15,16 |
H + H 2 O 2 = H 2 O + OH |
1,7e6 |
0 |
1900 |
7,3e5 |
0 |
9400 |
|
17,18 |
HO 2 + OH = H 2 O + O 2 |
1,0e7 |
0 |
0 |
1,35e8 |
0 |
36480 |
|
19,20 |
H 2 O 2 + O = HO 2 + OH |
2,8e7 |
0 |
3200 |
6,25e6 |
0 |
9990 |
|
21,22 |
HO 2 + HO 2 = H 2 O 2 + O 2 |
8,5e6 |
0 |
500 |
5,14e7 |
0 |
21670 |
|
23,24 |
H + O 2 = OH + O |
2,2e8 |
0 |
8450 |
1,3e7 |
0 |
0 |
|
25,26 |
H + O 2 + M = HO 2 + M |
5,0e3 |
0 |
-500 |
7,0e9 |
0 |
23000 |
|
27,28 |
2OH = H 2 O + O |
6,3e6 |
0 |
550 |
6,8e7 |
0 |
9240 |
|
29,30 |
2O + M = O 2 + M |
1,1e3 |
0 |
0 |
4,51e11 |
0,35 |
59960 |
|
31,32 |
H + HO 2 = H 2 + O 2 |
2,5e7 |
0 |
350 |
5.5e7 |
0 |
29100 |
|
33,34 |
HO 2 + H 2 = H 2 O + OH |
1,2e5 |
0 |
12080 |
1,25e3 |
0,44 |
38820 |
|
35,36 |
OH + H 2 O 2 = H 2 O + HO 2 |
1,0e7 |
0 |
910 |
2,8e7 |
0 |
16500 |
|
37,38 |
2OH = H 2 + O 2 |
6,17e5 |
0 |
12830 |
1,91e8 |
0 |
21890 |
|
39,40 |
H + HO 2 = H 2 O + O |
1,0e7 |
0 |
0 |
8,69e6 |
0 |
28330 |
|
41,42 |
OH + M = O + H + M |
1,57e10 |
0 |
51460 |
1,0e4 |
0 |
0 |
|
43,44 |
HO 2 + O = OH + O 2 |
1,0e7 |
0 |
0 |
1,33e6 |
0,27 |
27600 |
В данном механизме реакции участвуют 9 компонентов:
H 2 , O 2 , N 2 , H 2 O, H, O, OH, HO 2 , H 2 O 2 .
Анализ результатов
Проведение расчетов связано с выявлением соотношений точности и скорости счета для различных кинетик. Так для реакции окисления водорода был получен ряд результатов, отображенный на рисунке.
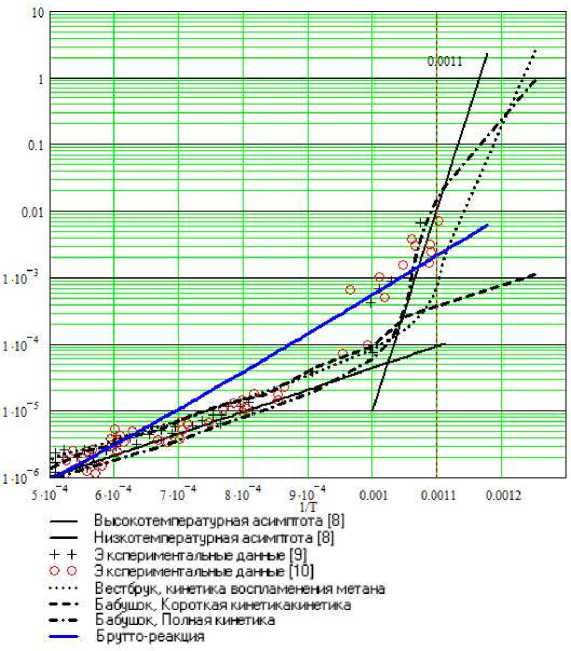
Зависимость адиабатического периода индукции от температуры
Как видно из графика, экспериментальные данные распределены вдоль двух асимптот, рассмотренных в [8]. Наиболее точное описание экспериментальных данных удалось получить, используя полную кинетику [7]. Использование сокращенной кинетики [6] допустимо лишь для описания высокотемпературной асимптоты, а упрощение механизма до одной брутто-реакции пригодно лишь для приблизительных оценок, хотя во многих случаях достаточно и этого, особенно если принимать во внимание скорость счета при использовании такой кинетики.
Работа выполнена при поддержке РФФИ. Грант № 13-01-00072.
Список литературы Математическое моделирование адиабатического теплового взрыва для реакции окисления водорода
- Bode Shrestha, S.O. Hydrogen as an Additive to Methane for Spark Ignition Engine Applications/S.O. Bode Shrestha, G.A Karim//Intern. J. of Hydrogen Energy. -1994. -V. 24, № 5. -P. 521-586.
- Гельфанд, Б.Е. Водород: параметры горения и взрыва/Б.Е. Гельфанд, О.Е. Попов. -М.: Физматлит, 2008.
- Рябинин, В.К. Математическое моделирование адиабатического периода индукции для метан-кислородных смесей в широком диапазоне начальных давлений и температур/В.К. Рябинин, Ю.М. Ковалев//Вестник ЮУрГУ. Серия: Математическое моделирование и программирование. -2013. -Т. 6, № 1. -С. 56-71.
- Варнатц, Ю. Горение. Физические и химические аспекты, моделирование, эксперименты, образование загрязняющих веществ/Ю. Варнатц, У. Маас, Р. Диббл. -М.: Физматлит, 2003.
- Бабушок, В.И. Глобальные кинетические параметры для высокотемпературных газофазных реакций/В.И. Бабушок, А.Н. Дакданча//ФГВ. -1993. -№ 4. -С. 48-80.
- Бабушок, В.И. Тестовые примеры моделирования кинетики сложных реакций/В.И. Бабушок, А.Н. Дакданча. -Красноярск, 1990.
- Максимов, Э.И. Физическое моделирование химических процессов в реакторе идеального перемешивания/Э.И. Максимов, А.Г. Мержанов//ДАН СССР. -1975. -Т. 6, № 2. -С. 402-405.
- Димитров, В.И. Простая кинетика/В.И. Димитров. -Новосибирск: Наука, 1982.
- Mullins, B.P. Studies of the Spontaneous Ignition of Fuels Injected into a Bot Air Stream/B.P. Mullins. -NATO AGARD AG S/P2. 1952.
- Patch, R.W. Shock-Tube Measurement of Dissociation on Rates of H2-J chem/R.W. Patch//J. Chem. Phys. -1962. -V. 36, № 7. -6 p.


