Математическое моделирование аппланационного нагружения глазного яблока с учетом нелинейности упругих свойств роговицы
Автор: Моисеева И.Н., Штейн А.А.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 3 (89) т.24, 2020 года.
Бесплатный доступ
Выполнено математическое моделирование деформации глазного яблока, нагруженного тяжелым штампом с плоским основанием, что соответствует тонометрии по Маклакову. Моделирование осуществляется в рамках развиваемого авторами общего подхода, представляющего глазное яблоко как совокупность деформируемой двумерной поверхности (роговица) и нульмерного элемента, откликающегося изменением объема на изменения внутриглазного давления (склеральная область). Поведение обоих компонентов считается упругим: линейно для склеральной области и нелинейно для роговицы. Для последней использована разработанная авторами ранее экспоненциальная модель, в которой нелинейность упругих свойств роговицы характеризуется единственным параметром. Расчеты проводились в диапазоне значений параметра нелинейности, оцененном на основании данных о растяжении изолированной роговицы давлением. Показано, что учет нелинейности приводит к увеличению разницы между давлениями в нагруженном и ненагруженном глазу (тонометрической разности) и возрастанию наклона зависимости тонометрического давления от веса груза (коэффициента эластоподъема) при эластотонометрии. Рассчитанные поправки позволяют предложить уточнения для методики обработки данных клинических измерений. Однако такого рода выводы следует рассматривать как предварительные: окончательные оценки параметра нелинейности для живых глаз отсутствуют и должны быть получены в результате сопоставления результатов расчета с клиническими исследованиями. В частности, необходимо выяснить, в какой степени значения этого параметра индивидуальны и могут различаться для разных глаз.
Глаз, роговица, нелинейные упругие свойства, внутриглазное давление, тонометрия по маклакову, математические модели
Короткий адрес: https://sciup.org/146282172
IDR: 146282172 | УДК: 531/534: | DOI: 10.15593/RZhBiomeh/2020.3.01
Текст научной статьи Математическое моделирование аппланационного нагружения глазного яблока с учетом нелинейности упругих свойств роговицы
Моисеева Ирина Никитична, к.ф.-м.н., с.н.с. Института механики, Москва
Штейн Александр Александрович, к.ф.-м.н., в.н.с. Института механики, Москва решения корректных механических задач для разработки практически важных критериев и рекомендаций, основывающихся на данных измерений, имеется в настоящее время у многих врачей и разработчиков медицинской аппаратуры. Потребность в таких исследованиях особенно возросла в последнее время в связи с высокой частотой разнообразных хирургических воздействий на глаза. Для таких глаз традиционные методы клинической оценки их механических свойств и механического состояния зачастую оказываются несостоятельными.
Непосредственно связанные с измерениями воздействия испытывает, как правило, роговица. Если испытание выполняется за достаточно длительное время, чтобы установилось статическое состояние, решающую роль играют упругие свойства. Между тем упругие свойства роговицы весьма сложны, недостаточно изучены и сильно индивидуальны. Роговица анизотропна и пространственно неоднородна по всем направлениям, а связь напряжений с деформациями в ней нелинейна [9, 11–13, 16, 18]. Кроме того, роговица неоднородна геометрически: ее толщина и кривизна существенно меняются от центральной точки (апекса) к периферии. Тем не менее при моделировании многих механических процессов, в том числе статической тонометрии, эффективными оказываются относительно простые модели, рассматривающие роговицу как изотропную и в тангенциальном направлении однородную линейно упругую оболочку. Нами разработан [4] максимально упрощенный подход к механике глазного яблока, который учитывает небольшое количество подлежащих определению параметров и оказался полезен при моделировании различных типов тонометрии. В рамках этого подхода роговица представляется безмоментной (мягкой) изотропной однородной, линейно-упругой двумерной поверхностью. Условие безмоментности оказывается основным допущением, позволяющим эффективно воспроизвести экспериментальные данные, не прибегая к сложным многопараметрическим моделям [1, 2].
Упрощающее допущение о линейности упругого поведения роговицы присутствует во многих теоретических исследованиях, в том числе и таких, где роговица рассматривается как трехмерное упругое тело. Тем не менее в выполняемых в настоящее время различными группами исследователей конечноэлементных расчетах нагружения роговицы нелинейность, как правило, предполагается. Иногда это нелинейность, непосредственно заложенная в программные пакеты, иногда используются те или иные упругие потенциалы в предположении конечности деформаций. Параметры, задающие нелинейность, оказываются в числе множества закладываемых в расчет параметров, и требуются специальные, достаточно произвольные, допущения, чтобы весь этот набор параметров конкретизировать.
В рамках нашего подхода было необходимо предложить такую модель нелинейно-упругого поведения роговицы, чтобы число характеризующих ее параметров увеличилось лишь незначительно по сравнению с линейным случаем. Таким образом, должно сохраниться основное преимущество нашего подхода: возможность определения всех параметров модели для индивидуального глаза в клинических испытаниях. В частности, возможен и ответ на вопрос, в какой степени необходим учет нелинейности в тех или иных задачах.
Эта задача была решена в работе [7], где была предложена и верифицирована по данным опытов, в которых раздувалась давлением изолированная роговица, максимально простая, физически корректная модель нелинейно-упругой роговицы как двумерной безмоментной поверхности. Оценки показывают, что для большинства практически важных ситуаций можно сохранить условие геометрической малости деформаций. Зависимость двумерных напряжений от деформаций в рамках этой модели экспоненциальная, причем при сохранении условия изотропии нелинейность характеризуется единственным дополнительным параметром по сравнению с линейным случаем. Порядок величины этого параметра оценен по упомянутым экспериментальным данным.
В предлагаемой работе на основе математического моделирования и численных расчетов исследуется, в какой степени нелинейное поведение роговицы может влиять на результаты аппланационной тонометрии по Маклакову.
С ИСТЕМА УРАВНЕНИЙ И МЕТОД РЕШЕНИЯ
Система уравнений равновесия и геометрических соотношений для роговицы как двумерной поверхности, использовавшаяся нами ранее (см., например, [4], (1.1)), может быть сохранена, так как остаются в силе все положенные в основу этой системы допущения: отсутствие сопротивления изгибу, однородность и изотропия упругих свойств вдоль поверхности, а также малость деформаций. Последнее условие не исключает конечности перемещений, что существенно при решении задач тонометрии.
Определяющие соотношения для усилий T и T (главных двумерных напряжений), действующих в меридиональном и перпендикулярном ему направлениях, принимаем в соответствии с [7] в виде
T = A[ B (exp( B 8, + C 82) - 1) + C (exp( B 82 + C 8,) - 1)] + T o, T = A [ B (exp( B 82 + C 8,) - 1) + C (exp( B 8, + C 82) - 1)] + T .
Здесь 8j и 82 - компоненты двумерного тензора деформации в направлении главных осей, диагональные компоненты этого тензора равны нулю в силу постановки задачи, а постоянная величина T определяется формулой T = pR / 2, где р0 - начальное давление, а R – радиус роговицы. Такое представление соответствует допущению, что при давлении p роговица имела форму сферического сегмента. Для параметров A , B и C имеют место соотношения
A =
E C
5 2 ( 1 -v c ) ’
B = 5
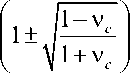
C = 5-B ,
где Ec и vc - упругие модули (модуль растяжения и коэффициент Пуассона) роговицы как двумерной, линейно-упругой поверхности при нулевых деформациях (т.е. при T = T = T ), а 5 - безразмерный параметр нелинейности. Далее будем использовать условный модуль растяжения материала роговицы E c в предположении, что она однородна и имеет стандартную толщину 5 = 0,5 мм. Этот модуль связан с Ес формулой Е * = 5 Ес .
При решении уравнений для роговицы используемая форма нелинейного определяющего соотношения делает целесообразным выбор иного набора определяемых переменных, чем мы традиционно использовали для линейной модели. В [4] и большинстве других наших публикаций этот набор включал наряду с двумя геометрическими параметрами усилие в меридиональном направлении T; теперь же удобнее выбирать вместо Тх деформацию в том же направлении 8, чтобы исключить использование неявных функций при преобразовании переменных. Соответственно, меняется асимптотическое условие в апексе (1.10) [4], которое теперь принимает вид s ^ 0: r ~ (1 + 8,)s, где s – независимая переменная, равная отсчитываемой от апекса длине дуги в начальном состоянии. Легко показать, что на поверхности слабого разрыва, разделяющей свободную и нагруженную тонометром области, переменная ε остается непрерывной, что позволяет заменить условие непрерывности T [4] условием непрерывности ^ . Остальные граничные условия, принятые в [4] для задачи о нагружении роговицы плоским штампом, остаются без изменений. Численное решение уравнений осуществлялось методом стрельбы с использованием схемы Рунге–Кутта четвертого порядка. Как всегда в задачах тонометрии, предполагалось сохранение после нагружения первоначального внутриглазного объема, равного сумме подроговичного и склерального объемов.
В соответствии с имеющимися оценками для жесткостей склеры и роговицы деформации склеры при не слишком высоких внутренних давлениях малы в сравнении с деформациями роговицы. В самом деле, считая роговицу и склеру сферическими сегментами радиусами R и R и толщинами δ и δ соответственно, оценим их тангенциальные деформации ес и ^ формулами в = (1 -vc )(ДрRc )/(2 5с Ес ) и s5 = (1 -v5 )( Д р Rs )/ (2 5 Es ), где Д р - изменение давления; Es - склеральная жесткость, а ν – коэффициент Пуассона материала склеры. Примем для входящих в эти формулы величин их средние нормальные значения [4]: Rc = 8 мм, Rs = 12 мм, 5С = 0,5 мм, 5$ = 1 мм, Ес = 0,3 МПа, Es = 10 МПа и учтем, что коэффициенты Пуассона имеют (в силу близости трехмерного материала к несжимаемому) одинаковый порядок v5 ~ vc ~ 0,5. Тогда гс /;; имеет порядок 0,5 - 102, т.е. деформация роговицы более чем на порядок превосходит деформацию склеры. Вследствие этого можно ожидать, что нелинейность будет проявляться в деформациях роговицы при намного меньших давлениях, чем в деформациях склеры. Поэтому при решении задачи об аппланационном (по Маклакову) нагружении глаза будем сохранять предположение о линейной связи между изменениями склерального объема и внутриглазного давления. Нелинейное деформирование склеры станет существенным, когда жесткость роговицы значительно возрастет вследствие нелинейности, а при дальнейшем повышении давления она практически перестанет деформироваться. Сформулированные соображения находятся в согласии с экспериментальными данными. Этому вопросу будет посвящена отдельная публикация.
При расчетах геометрические параметры роговицы выбирались соответствующими «среднему» глазу [4], коэффициент Пуассона ν полагался равным 0,45, а склеральная жесткость E равной ее нормальному значению 10 МПа. Во всех случаях за отсчетное принималось истинное давление, т.е. давление в ненагруженном глазу. Жесткость роговицы E выбиралась равной 0,3 или 0,6 МПа. В соответствии с выполненными в [7] оценками параметр нелинейности ς варьировался в диапазоне от 1 (что соответствует практически линейному поведению) до 90.
Р ЕЗУЛЬТАТЫ РАСЧЕТОВ
Исследуем влияние параметра нелинейности роговицы на тонометрическую разность Δp = p - p , т.е. на разность между тонометрическим давлением (под грузом) pt и истинным (в ненагруженном глазу) р0. Именно эта величина определяет пересчет от геометрического параметра, непосредственно определяемого при измерении (диаметра пятна контакта тонометра с роговицей), к искомому внутриглазному давлению, отождествляемому с p . На рис. 1 представлена зависимость тонометрической разности от параметра нелинейности при двух стандартных весах тонометра. Рис. 2 демонстрирует влияние на тонометрическую кривую жесткости роговицы при одном и том же весе тонометра и разных параметрах нелинейности. На рис. 2, а вес тонометра G = 5 Г, а на рис. 2, б G = 15 Г. Это минимальный и максимальный стандартные веса груза в тонометре Маклакова.
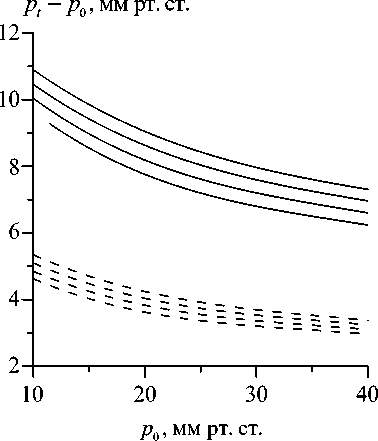
Рис. 1. Зависимость тонометрической разности от истинного давления при разных значениях параметра нелинейности и веса тонометра. Для нижнего семейства кривых вес тонометра G = 5, а для верхнего G = 10 Г. Параметр нелинейности в кривых каждого семейства (снизу вверх) g = 1, 30, 60, 90. Жесткость роговицы
Е = 0,6 МПа c ,
Как видно из этих рисунков, форма зависимости A p ( p 0) при учете нелинейной упругости роговицы практически не меняется, однако с увеличением параметра нелинейности тонометрическая разность несколько возрастает (тонометрические кривые с ростом g , сохраняя в целом свою форму, сдвигаются вверх по оси ординат). С увеличением веса тонометра влияние нелинейности на тонометрическую разность становится более значительным, однако даже для максимального стандартного веса G = 15 Г остается умеренным: при g = 90 тонометрическая разность увеличивается по сравнению с линейным случаем на величину около 2 мм рт. ст. При G = 5 Г это различие не превосходит 1 мм рт. ст.
Влияние давления на зависимость тонометрической разности от параметра нелинейности различно для разных весов груза. При большом весе тонометра ( G = 15 Г) тонометрическая разность растет равномерно по давлению: ее приращение за счет нелинейности приблизительно одинаково при малых и больших давлениях. С возрастанием жесткости роговицы, как и в линейном случае, тонометрическая разность уменьшается. При малом весе груза ( G = 5 Г ) для мягкой роговицы появляется заметная зависимость увеличения тонометрической разности от давления: если для Ес = 0,3 МПа ее увеличение по сравнению с линейным случаем при том же параметре нелинейности и малых давлениях приблизительно такое же, как и для Ес = 0,6 МПа, то при р 0 = 40 мм рт. ст. это увеличение вдвое меньше.
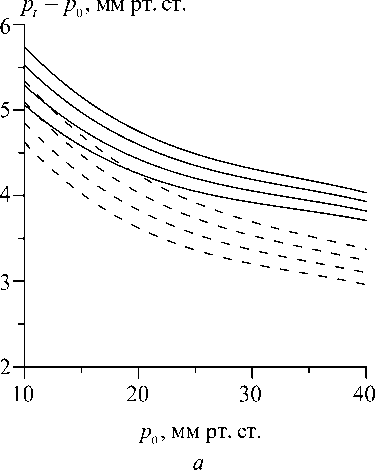
Рис. 2. Зависимость тонометрической разности от истинного давления при разных значениях параметра нелинейности и жесткости роговицы. Вес тонометра равен 5 (а) и 15 (б) Г. Семейства пунктирных кривых соответствуют Ес = 0,6, а сплошных – 0,3 МПа. Параметр нелинейности в кривых каждого семейства равен (снизу вверх) g = 1,30, 60, 90
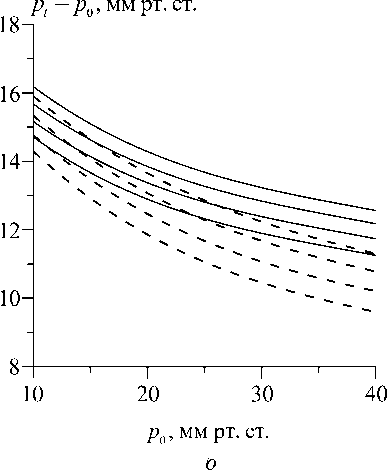
На рис. 3 исследовано влияние параметра нелинейности роговицы на зависимость тонометрического давления в одном и том же глазу от веса тонометра. Как и в линейном случае, которому на графике практически соответствует значение g = 1, кривые pt ( G ) близки к линейным зависимостям, что позволяет ввести коэффициент эластоподъема у как наклон соответствующей прямой.
pt , мм рт. ст.
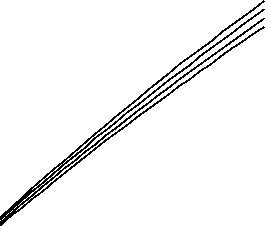
0 4 8 12 16
G , Г
Рис. 3. Зависимость тонометрического давления от веса тонометра при Ес = 0,3 МПа, р0 = 12 мм рт. ст. и различных значениях параметра нелинейности: на линиях снизу вверх g = 1, 30, 60, 90
Если бы зависимости p ( G ) были в точности линейными (и линии на рис. 3 в точности прямыми), коэффициент у можно было бы определять по формуле
Pt 2 - Pt 1
G 2 - G/ где цифровым индексом 1 или 2 обозначен номер измерения, причем результат не зависел бы от выбора весов для измерений. В клинике при выполнении эластотонометрии пользуются именно формулой (3) при раз и навсегда фиксированных весах тонометра (обычно Gx = 5 и G2 = 15 Г). Более надежно проведение этой измерительной процедуры с наложением нескольких стандартных весов и проведением наилучшим образом соответствующей им прямой, например, методом наименьших квадратов [3]. Такой подход позволяет как учесть слабую нелинейность зависимости p(G), так и ослабить влияние ошибок измерения. Пока мы остаемся в рамках теоретического рассмотрения, оба метода дают близкие результаты.
Зависимостям, изображенным на рис. 3, соответствуют значения коэффициента эластоподъема (снизу вверх, т.е. в направлении возрастания параметра нелинейности) Y = 0,93, 0,965, 0,995, 1,02 мм рт. ст. / Г. В таблице приведены также значения у для истинного давления р 0 = 16 мм рт. ст. и двух разных значений жесткости роговицы Ес = 0,3 и 0,6 МПа. Коэффициент эластоподъема вычислялся по формуле (3) с Gx = 5 и G 2 = 15 Г.
Значения коэффициента эластоподъема у при рц = 16 мм рт. ст.
|
Модуль упругости |
Z = 1 |
Z = 30 |
Z = 60 |
Z = 90 |
|
E c = 0,3 МПа |
0,9 |
0,92 |
0,955 |
0,985 |
|
E c = 0,6 МПа |
0,875 |
0,91 |
0,95 |
0,985 |
Из рис. 3 и таблицы видно, что при той же начальной жесткости роговицы коэффициент эластоподъема у оказывается с учетом нелинейности выше, чем без ее учета, и растет с возрастанием параметра нелинейности q . При максимальном рассмотренном значении этого параметра q = 90 коэффициент у возрастает по сравнению с линейным случаем ( q = 1 ) на величину порядка 10%. При возрастании параметра нелинейности значения коэффициента эластоподъема, соответствующие различным жесткостям роговицы, постепенно сближаются и при Z = 90 для рассмотренных значений параметров практически совпадают.
О БСУЖДЕНИЕ
Посмотрим сначала, как учет нелинейности упругого поведения роговицы влияет на решение основной задачи тонометрии – определения внутриглазного давления. В диапазоне изменения параметра нелинейности Z е [60,90], соответствующем данным о раздувании давлением изолированной роговицы [7], учет нелинейности приводит к увеличению тонометрической разности по сравнению с линейным случаем. Это увеличение не превышает 1 мм рт. ст. для тонометра весом G = 5 Г и может доходить до 2 мм рт. ст. при G = 15 Г. С учетом возрастания тонометрической разности при увеличении веса тонометра ошибка при расчете истинного давления по тонометрическому на основе линейной модели не превосходит 10% от разности между ними, что не слишком значительно практически. Однако при оценке истинного давления по тонометрическому учет поправки на нелинейность может повысить точность этой оценки. На такую поправку мало влияют начальная жесткость роговицы и величина давления – она становится заметно меньше лишь для наиболее легкого тонометра с G = 5 Г при высоком давлении и достаточно малой жесткости - порядка нормальной, Ес = 0,3 МПа, или меньше.
При эластотонометрии нелинейность роговицы проявляется в некотором увеличении коэффициента эластоподъема у на величину до 10% при истинном давлении р0 = 12 - 16 мм рт. ст. С ростом параметра нелинейности коэффициент эластоподъема становится мало зависимым от начальной жесткости роговицы, и процедура оказывается менее пригодной для оценки этой жесткости. При больших q коэффициент у зависит в основном от склеральной жесткости и истинного давления (точнее, от их отношения E / p [6]). Это упрощает обработку результатов эластотонометрии (поскольку остается единственный определяемый параметр), но снижает ее информативность. Как и в линейном случае, с ростом давления влияние жесткостей (в том числе жесткости роговицы) на коэффициент эластоподъема усиливается (из-за уменьшения безразмерных параметров E / p и E / p ) [3].
Сформулированные соображения остаются, в известной мере, условными. Дело в том, что вопрос о нелинейности упругого поведения глазных тканей в живом глазу остается открытым. Выполненная оценка параметра нелинейности основывается на опытах с мертвой роговицей [8, 10]. Представления о нелинейности упругого отклика на внутреннее давление глазного яблока в целом также опираются на данные о раздувании вводимыми объемами жидкости энуклеированного глаза [14, 17]. Между тем немногочисленные аналогичные эксперименты на живом глазу указывают на практически линейное растяжение в широком диапазоне физиологически допустимых давлений [15]. Отметим еще, что расчеты по нашей модели с учетом нелинейности роговицы оказались несколько более удаленными от данных, представленных в известных таблицах Нестерова–Вургафта [5], чем результаты, рассчитанные по линейной модели. Как и все остальные рассогласования, это несовпадение не является критическим, поскольку упомянутые таблицы получены на энуклеированных глазах с использованием осреднения и при не вполне ясных условиях экспериментов. Это лишь дополнительный довод в пользу необходимости дальнейших исследований.
Единственный адекватный путь для оценки параметров нелинейного глаза – измерения на конкретном живом глазу без осреднения полученных результатов и определение на основе нашей малопараметрической модели индивидуальных значений входящих в нее упругих характеристик: роговичной и склеральной жесткостей и параметра нелинейности для роговицы. Как уже говорилось выше, при достаточно больших давлениях (например, развивающихся под тонометром Шиотца), возможно, окажется существенным еще и аналогичный параметр нелинейности для склерального сегмента. Про обе характерные жесткости мы уже с несомненностью знаем, что для разных глаз они значительно различаются, и эти различия необходимо учитывать при обработке результатов клинических измерений. Имеет ли место подобный разброс для параметров нелинейности, предстоит еще выяснить. В конечном счете должна быть разработана схема измерений с использованием разнотипных тонометров для определения как внутриглазного давления, так и всего представительного набора параметров, определяющих упругое поведение конкретного живого глаза.
З АКЛЮЧЕНИЕ
Выполнено численное моделирование деформирования глазного яблока под действием тяжелого широкого штампа с плоским основанием (тонометра Маклакова) с учетом нелинейности упругого поведения роговицы. В отличие от сходных исследований, имеющихся в литературе, использована предложенная нами ранее оригинальная модель, характеризующая упругие свойства глаза небольшим числом параметров: в случае нелинейно-упругой роговицы, пространственно однородной и изотропной в тангенциальном направлении, их четыре, из которых лишь три существенны. Расчеты проведены в диапазоне значений параметра нелинейности, оцененном нами на основании данных опытов, выполненных на изолированной роговице.
Оценены поправки, вносимые учетом нелинейности в оценку истинного давления по тонометрическому, а также влияние такого учета на интерпретацию результатов эластотонометрии. Тем не менее остается открытым вопрос о возможности использования для живого глаза значений параметра нелинейности, найденных для мертвой роговицы. Окончательный ответ на этот вопрос требует проведения клинических экспериментов. Выполненное исследование представляет собой очередной шаг на пути к разработке полностью корректной методики оценки механических свойств и механического состояния индивидуального глаза. Такая оценка откроет путь к дальнейшему повышению информативности офтальмологических измерений и разработке новых научно обоснованных диагностических методик.
Б ЛАГОДАРНОСТИ
Работа выполнена в рамках Госпрограммы АААА-А19-119012990119-3.
Механика жидкости и газа. – 2010. – № 2. – С. 12–22.
Список литературы Математическое моделирование аппланационного нагружения глазного яблока с учетом нелинейности упругих свойств роговицы
- Бауэр С.М., Любимов Г.А., Товстик П.Е. Математическое моделирование метода Маклакова измерения внутриглазного давления // Изв. РАН. Механика жидкости и газа. - 2005. - № 1. -С. 24-39.
- Любимов Г.А., Моисеева И.Н., Штейн А.А. О повышении информативности теста тонометрии // Нац. журн. глаукома. - 2015. - Т. 14, № 4. - С. 58-65.
- Любимов Г.А., Моисеева И.Н., Штейн А.А., Иомдина Е.Н., Арчаков А.Ю., Киселева О.А. О возможности использования параметров, характеризующих упругие свойства корнеосклеральной оболочки глаза, для диагностики ее измененного механического состояния при первичной открытоугольной глаукоме // Российский журнал биомеханики. - 2018. - Т. 22, № 1. - С. 8-18.
- Моисеева И.Н., Штейн А.А. Анализ зависимости давление-объем для глазного яблока, нагруженного плоским штампом, на основе двухсегментной упругой модели // Изв. РАН. Механика жидкости и газа. - 2011. - № 5. - С. 3-15.
- Нестеров А.П., Бунин Ф.Я., Кацнельсон Л.А. Внутриглазное давление. Физиология и патология. -М.: Наука, 1974. - 381 с.
- Штейн А.А. О зависимости давление-объем для нагруженного извне глазного яблока // Изв. РАН. Механика жидкости и газа. - 2010. - № 2. - С. 12-22.
- Штейн А.А., Моисеева И.Н., Любимов Г.А. Математическая модель роговицы глаза с учетом экспоненциальной нелинейности ее упругих свойств при условии геометрической малости деформаций // Российский журнал биомеханики. - 2019. - Т. 23, № 3. - С. 375-390.
- Bryant M.R., McDonnell P.J. Constitutive laws for biomechanical modeling of refractive surgery // J. Biomech. Eng. - 1996. - Vol. 118, no. 4. - P. 473-481.
- Corneal biomechanics and refractive surgery / Ed. by F.A. Guarnieri. - Berlin: Springer, 2015. - 146 p.
- Elsheikh A., Alhasso D., Rama P. Biomechanical properties of human and porcine corneas // Exp. Eye Res. - 2008. - Vol. 86. - P. 783-790.
- Fernandez D.C., Niazy A.M., Kurtz R.M., Djotyan G.P., Juhasz T. Finite element analysis applied to cornea reshaping // J. Biomed. Opt. - 2005. - Vol. 10, no. 6. - 064018. - P. 1-11.
- Fu J., Haghighi-Abayneh M., Pierron F, Ruiz P.D. Depth-resolved full-field measurement of corneal deformation by optical coherence tomography and digital volume correlation // Exp. Mech. - 2016. -Vol. 56, no. 7. - P. 1203-1217.
- Hjortdal J.0. Regional elastic performance of the human cornea // J. Biomech. - 1996. - Vol. 29, no. 7. -P. 931-942.
- Macri F.J., Wanko T., Grimes P.A. The elastic properties of the human eye // AMA Arch. Ophthalmol. -1958. - Vol. 60, no. 6. - P. 1021-1026.
- Pallikaris I.G., Kymionis G.D., Ginis H.S., Kounis G.A., Tsilimbaris M.K. Ocular rigidity in living human eyes // Invest. Ophthalm. Vis. Sci. - 2005. - Vol. 46, no. 2. - P. 409-414.
- Reichel E., Miller D., Blanco E., Mastanduno R. The elastic modulus of central and perilimbal bovine cornea // Ann. Ophthalmol. - 1989. - Vol. 21. - P. 205-208.
- Ridley F. The Intraocular Pressure and Drainage of the Aqueous Humour // Brit. J. Exp. Pathol. - 1930. -Vol. 11, no. 4. - P. 217-240.
- Shin T.J., Vito R.P., Johnson L.W., McCarey B.E. The distribution of strain in the human cornea // J. Biomech. - 1997. - Vol. 30, no. 5. - P. 497-503.


