Математическое моделирование циклических режимов управления температурой при реализации полимеразной цепной реакции (ПЦР) для метода молекулярных колоний (ММК) на микрочипе

Для реализации полимеразной цепной реакции в реальном масштабе времени (ПЦР-РВ), в частности для метода молекулярных колоний (ММК), необходимо осуществить многостадийный циклический режим изменения температуры (например, см. [1]). При этом число циклов может меняться от 20–40 при ПЦР до сотен при ММК. Особенность, связанная с реализацией указанных методов на микрочипе при определяющем размере (толщине) реакционной камеры, сопоставимом с 1 мм, состоит в том, что возможно выполнять нагрев/охлаждение камеры с существенно большей скоростью по сравнению с конструктивными макроаналогами, т. е. 10 град/с и более. Иллюстрация типового циклического температурного режима представлена на рис. 1.

Каждая стадия цикла (денатурация, отжиг, синтез) должна осуществляться гарантированное время при температурах, близких к заданным на графике рис. 1, поскольку иначе необходимая трансформация молекул ДНК может не осуществиться. В то же время нагрев/охлаждение реактора может быть максимально ускорен. Таким образом, задача математического моделирования и соответствующих расчетов заключается в оценивании минимально необходимого времени реализации каждой стадии цикла и в конечном счете минимизации времени проведения ПЦР или ММК.

Помимо решения основной проблемы — анализ динамики средней (либо критической,

• т. е. минимальной) температуры реакционной камеры — в работе рассмотрены сопутствующие задачи:

• а)    построение практически удобных аппроксимаций решений либо полиномами низкой степени, либо степенными зависимостями;

• б)    описание особенностей реализации вычислительной процедуры обратной прогонки, в первую очередь формулировка условий, связанных со "склейками" трех решений;

• в)    анализ устойчивости решений в зависимости от ранга пространственной и временнóй дискретизации разностной схемы ( Δ x , Δ t ).

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОДЫ РЕШЕНИЯ

В качестве имитационной задачи рассмотрим двухстадийный процесс: линейный нагрев от 55 до 95 ºC с максимально возможной скоростью изменения (для примера, выбрано 10 град/с) и далее поддержание 3–5 с постоянной температуры 95 ºC. По-существу в зеркальном отражении подобное температурное управление соответствует стадиям перехода от денатурации к отжигу (стадия 1) и собственно отжигу (стадия 2). Для наглядности и удобства представления результата отсчет температуры ведется от нулевого уровня 55 ºC. Дальнейшие стадии реального температурного цикла ПЦР (согласно рис. 1) качественно повторяют выбранные нами две стадии.

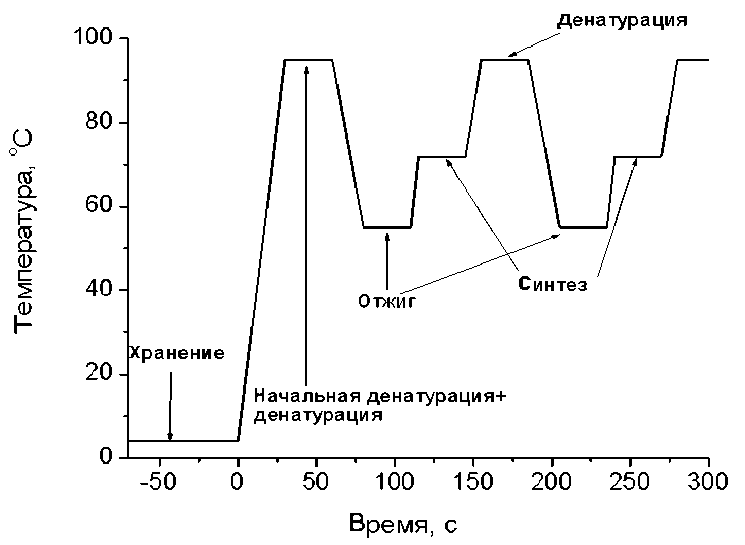
Рис. 1. Схема температурного управления при реализации ПЦР-РВ

Задано: T o = At		Формируется: T = f ( A , t , l„ 1 2 , a 021 )
Граница: Стекло: х = 0           a 12, k 1, l 1	Водоподобная сре- Стекло да: a 02, k 0, l 2                 a 12, k 1, l	:        Граница: х = 2 l + l 1           12

Граничные условия 4-го и 5-го рода:

Склейка температуры — T ( l + 0) = T ( l - 0)

5 T ( l - 0)      5 T ( l + 0)

Склейка потоков — k         = k

⁰     5 x        1     5 x

Рис. 2. Схема модельного объекта (микрореакционной камеры)

На рис. 2 иллюстрируются геометрическая и вычислительная схемы модельной задачи. Оценивается в первую очередь теплоперенос в вертикальном направлении (по глубине реакционной камеры). Возможны два способа управления температурой:

• 1)    наличие двух идентичных нагревателей (или одного и того же нагревателя), задающих управляющее значение температуры на обеих стеклянных стенках реакционной камеры (далее схема 1);

• 2)    задается температурное управление только одним нагревателем на одной из стенок; в этом случае нагрев другой стенки и как следствие мик-рореакционной камеры осуществляется опосредованно в результате нагрева воздуха в термостате

(далее схема 2).

Необходимым ограничением в схеме 2 будет возможность описания нагрева воздуха как задачи теплопереноса на бесконечной прямой с заданным граничным условием при х = 0 и нулевым начальным условием. Т. е. рассматриваются размеры микрореакционной камеры, пренебрежимо малые по сревнению с размерами термостата, и времена, далекие от режима выхода температуры на асимптоту (т. е. порядка нескольких секунд).

Физико-химические и геометрические характеристики объекта

Толщина стеклянных стенок      l1 = 0.1 - 0.3мм, высота реакционной камеры     12 = 0.7 - 1.0мм.

Коэффициент термодиффузии (температуропроводности):

водоподобная (гелевая) среда — a 02 = 0.00140см²/с, стекло — а 2 = 0.00616 см² / с.

Аппроксимации коэффициентов теплопроводности в зависимости от температуры приведены, в частности, в [2]:

для водоподобной среды к0 -104 = 0.61 + 0.0012(T - 298)Дж/(м - К - с), для стеклянной стенки к1 -104 = 1.38 + 0.0013(T-298)Дж/(м- К-с).

Температура Т дается по абсолютной шкале. Изменение температуры на 40 град приводит к изменению коэффициентов теплопроводности на 5– 6 %. Этими изменениями можно пренебречь при оценочных расчетах либо учесть при численных расчетах.

Коэффициент температуропроводности воздуха полагаем a ² = 0.202 см² /с >>  a 2 .

Предполагается доминирование теплопереноса в вертикальном направлении (по глубине реакционной камеры). Соответственно решается пространственно-одномерная задача (дифференциальное уравнение в частных производных второго порядка параболического типа) с необходимостью "склейки" трех решений.

Использована неявная конечно-разностная схема с решением соответсвующей системы уравнений методом обратной прогонки (факторизации). Детальное описание алгоритма реализации метода обратной прогонки имеется, например, в [3]. Для тестирования вычислительной расчетной программы использованы упрощенные схемы (например, схема "усредненная изотропная среда"), для которых имеются компактные аналитические решения методом разделения переменных, представленные в [4].

Аналитическое решение при схеме управления 1 для "усредненной изотропной среды" кратко приведено ниже. Заметим, что геометрически задача обладает осевой симметрией (одинаковое управление на границах, равная толщина стенок, одинаковые физико-химические характеристики среды, в т. ч. и модельной "усредненной среды").

Управляющие температурные профили на границах:

шения в форме полинома степени не выше 1, сведение компоненты (одного из аддитивных слагаемых) к однородным граничным условиям первого или второго рода, построение ортогональной системы собственных функций и разложение по ним источникового слагаемого, а также начальных условий.

Для первой стадии — аналитическое решение уравнения

д Т д t

a ² д² T l² д z z

z = [0,1],

где z — относительная пространственная координата ( l — суммарная высота реакционной камеры и обеих стеклянных стенок или толщина "усредненной" пластинки).

Решение (при t <  t ₀):

T ( z , t ) = At -

4 A

—-7 x

π ³ a ² / l ²

At , T ⁽ t ) =L ( At 0 ,

0 <  t <  t 0 ;

t ₀ <  t <  t ₀ + St .

Для конкретизации выбрано: A = 10, t ₀ = 4 и St = 3 - 5 с. При этом классическая процедура предполагает выделение детерминированного ре-

1 - exp

+2

к = 0

- ^ п ²(2 к + 1)² t l

^-- sin((2 к + 1) nz ). (2 к + 1)³

Средняя по сечению температура:

< T ( t ) >= At - ^4T² π a / l

1 - exp

+2

1-- к=0

-

x

a^ п ²(2 к + 1)² t

(2 к + 1)⁴

.

При достаточно больших временах

< t ( t ) > ~ At -

A 12 a ²/ l ² .

Здесь использованы результаты, которые мож- 4

но получить при разложении y = x в ряд Фурье

по косинусам:

4      +^                   4

1 π           1 π

^^ П ⁴ = 90 ^ к ^0(2 к + 1)⁴ = 96 .

При x = 0.5 отклонение температуры от управляющей будет наибольшим. В соответствующей сумме синусы равны ( - 1) ^к . Аналогичное предыдущему разложение функции y = x ³ нечетным образом в ряд Фурье по синусам дает сумму ряда

^2- ( - 1) ^к = П 3 1 :0(2 к + 1) ³ = 32

.

Значения приведенных выше сумм числовых рядов имеются в справочниках, например в [5]. Соответственно максимальное асимптотическое

a

a

дится нормированное время т = — 1 ; т ₀ = — 1 ₀.

"отставание" температуры будет

A 8 a ²/ l ²

Тогда

. Следует

обратить внимание, что "отставание" температуры реактора от управляющих значений пропорционально скорости ее изменения ( А ). Однако уменьшение А , очевидно, приводя к лучшему отслеживанию управления, будет сопровождаться соответ-

T ( x ,т ) = f ( x ,т ) =

Aτ a ² / l ²

^ к 2

2 1 + —

к к

2 τ

1 - erf к

x

—

2 τ

ствующим увеличением времени перехода от одной стадии цикла ПЦР к другой. Таким образом, имеет практический смысл задача поиска оптимального значения А , при котором обеспечивается

-

-    )

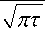
к 41 JJ

т <  т

0 ;

T ( x,т ) = f ( x,т ) - f ( x,т - т о ),   т >  т 0 .

минимизация времени цикла.

Оценим эти отклонения по средневзвешенному коэффициенту температуропроводности:

на 2 участках (стеклянных стенках по 0.2 мм) a ²= 0.00616, на оставшемся участке длиной 0.8 мм a ²= 0.00140. Усредненное значение можно получить как арифметическое, геометрическое и гармоническое средние: соответственно 0.00298, 0.00229 и 0.00190 см²/с.

Соответственно "отставание" средней температуры от температуры управляющего нагревателя будет при различных моделях "усреднения среды" около 4.0, 5.2 и 6.3 град. Это отставание достигает максимального значения примерно к 3.5 с, а далее практически стабилизируется. Очевидно, что на оси (при z = 0.5) отклонение температуры будет наибольшим.

Решение уравнения теплопроводности при ¹ >  ¹ 0 :

(Здесь erf(*) — интеграл вероятностей).

Задав x = 1, получим второй управляющий температурный профиль. Соответствующие значения управляющей температуры приведены в табл. 1.

Аппроксимации зависимостей, приведенных в табл. 1:

T₁(1 ) = 7.217 1 + 0.364 1 ²        (0 <  1 <  4);

? ; ( 1 ) = 34.322 + 2.000 3 1 - 4 (4 <  1 <  8).

T ( z , 1 ) = At о +

+x

+E ^k exp k=0

(

- к

a-n ²(2 k + 1)²( 1 - 1 о ) sin((2 k + 1) nz ),

1                       J

4 At ₀            4 A

n (2 k +1)    a ²/ 1²n ³(2 k +1) 3

Первая аппроксимация учитывала физическое ограничение T (0) = 0. Тем самым число степеней свободы для построения аппроксимирующей параболы было уменьшено до 2 (данное решение, таким образом, является квазиоптимальным). Формальное решение по МНК с построением аппроксимирующей параболы могло в среднем быть более точным, но при этом не удовлетворять вышеуказанному физическому ограничению.

На рис. 3 проиллюстрирован алгоритм температурного управления при схеме 2 ( А = 10 град/с). На левой стенке (кривая "управл.1") закон управления в соответствии с (1), на правой стенке (кривая "управл.2") величины температуры соответствуют данным табл. 1 (зависимостям (3)). Разумеется, при реализации схемы 1 и на первой, и на второй стадии задается T = Т ₀.

I I a2 „ xl 1 - exp I -—n2(2k +1)210

.

Краткое описание алгоритма формирования температурного управления на второй грани в зависимости от управляющего температурного профиля T ₀ ( t ) при реализации схемы 2 приведено далее. Управление на другой грани формируется в соответствии с более быстрым нагревом воздуха. Данная схема может рассматриваться как нагрев полубесконечного пространства. Подобная задача при заданном линейном и постоянном температурном профиле на границе x = 0 имеет известное решение, в частности приведенное в [3].

Для удобства представления результата вво-

Табл. 1. Зависимость температуры на внешней стеклянной стенке при заданной температуре нагревателя, согласно (3)

Время, с	Т , ºС
1	7.326
2	16.083
3	25.128
4	34.322
5	36.285
6	36.889
7	37.250
8	37.500

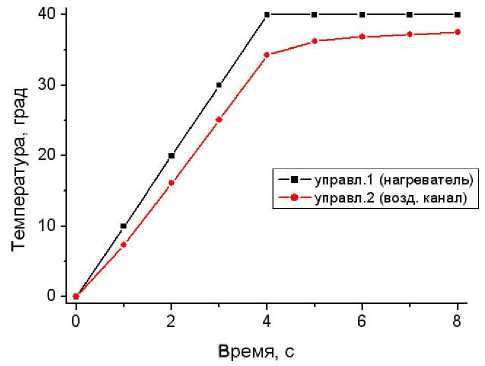
Рис. 3. Зависимость температуры на внешних гранях стеклянных стенок при схеме 2

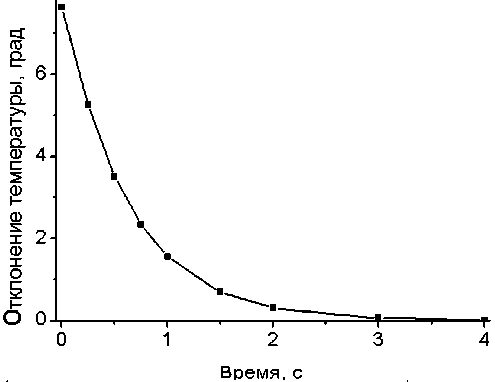
Рис. 5. Зависимость величины отклонения средней температуры реакционной камеры от заданного на второй стадии цикла значения 40 град при схеме 1

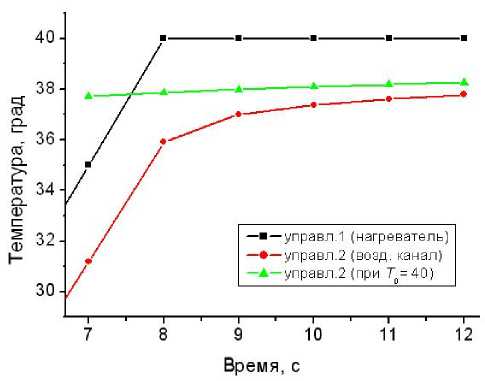
Рис. 4. Зависимость управляющей температуры на второй стеклянной стенке от задаваемой температуры нагревателя

На рис. 4 приведен фрагмент температурных зависимостей, соответствующий завершению стадии 1 и осуществлению стадии 2, т. е. завершение линейного роста управляющей температуры нагревателя и переход к стабилизации температуры 40 град (на графике кривая "управл.1"). Формируемая в соответствии со схемой 2 температура на другой стеклянной стенке представлена на рис. 4 как кривая "управл.2 (возд. канал)". Для сравнения на рис. 4 представлен расчетный профиль температуры на другой стеклянной стенке для случая, когда нагреватель с начального момента времени был бы нагрет до 40 град (кривая "управл.2 (при

Т 0 = 40)"). Для удобства сопоставления данных рассмотрен нагрев со скоростью 5 град/с. Таким образом, до 6–7 с различие между реально достигнутой температурой нагревателя 5 t и 40 град значительное.

Сравнительный анализ кривых показывает, что начиная с 8 с расхождение кривых "управл.2" незначительное. Таким образом, ключевую роль играет управляющая температура в текущий момент времени и на небольшом предшествующем интервале. Температура, заданная на начальном этапе измерения (на стадии 1 линейного нагрева) оказывает малое воздействие на температуру внешней стенки микрореакционной камеры на временах более 6 с, т. е. на стадии 2.

Далее на рис. 5 иллюстрируется форма переходного процесса при стабилизации управляющей температуры 40 град (вторая стадия цикла). Схема управления 1; время отсчитывается от момента достижения управляющей температурой 40 град, т. е. с 4-й с от начала цикла.

Анализ указанной зависимости, в частности построение оптимальной аппроксимации по МНК, осуществляется по традиционной процедуре. Выбор типа функциональной зависимости сделан в соответствии с алгоритмом, описанным в [6] и детализированным впоследствии в [7]. Этот выбор предполагает анализ арифметических, геометрических и гармонических средних входной и выходной величин. Поскольку анализ зависимости на рис. 5 выявил наименьшее расхождение Y „_om = Y ( X ар ), то оптимальной по МНК аппроксимацией будет ln( Y ) = AX + B , или Y = B exp( AX ).

Конкретные значения — Δ T ≅ 7.89exp( - 1.62 t ).

Нетрудно заметить, что численный множитель 7.89 примерно соответствует начальному отклонению 7.64. Другой коэффициент 1.62 примерно соответствует единице, деленной на первую (наименьшую) постоянную времени в формуле (2), а a2

именно 2 π2 при общей длине l = 0.12 см, а вели- чине a2 — усредненному коэффициенту термодиффузии (по стеклянной стенке и водоподобной гелевой среде). При использовании различных средних оценок коэффициента термодиффузии, приведенных ранее в статье, расчетные первые коэффициенты в экспоненциальных слагаемых (2) будут 2.04, 1.57 или 1.31 соответственно, что сопоставимо с 1.62.

Особенности реализации метода обратной прогонки применительно к выбранной схеме управления

• 1.    Выбор неявной конечно-разностной схемы обусловлен тем, что устойчивость явной разностной схемы требует выполнения условия: Δ t < Δ x ² /2 . При малой пространственной дискретизации шаг по времени крайне мал (порядка 10^–6 и менее). Для удобства "склейки" значений тепловых потоков на всех трех участках (обе стенки и реакционная камера) взято одинаковое значение Δ x .

• 2.    Метод обратной прогонки (факторизации) ориентирован на решение систем с т. н. трехдиагональной матрицей. В самой схеме метода предполагается следующая процедура: на основе коэффициентов уравнений строятся два массива прогоночных коэффициентов, на их основе вычисляется температура в каждой точке. Начальные значения прогоночных коэффициентов и температуры на границе определяются из граничных условий.

• 3.    В нашем случае необходимо построение трех решений (на трех участках). Явным образом задано лишь два граничных условия (температурный профиль на внешних границах участков 1 и 3). Соответственно на внутренних границах участков 1 и 3 должна осуществиться "склейка" температуры и теплового потока с решением на участке 2.

Таким образом, схема прогонки реализуется так: а) на основе граничных условий на участках 1 и 3 строятся по два массива прогоночных коэффициентов (начальные значения прогоночных коэффициентов известны, т. к. на границах реакционной камеры заданы значения температуры); б) из "склейки" решений на границе участков 1 и 2 получаем начальные значения для прогоночных коэффициентов на участке 2 (следовательно, все прогоночные коэффициенты становятся известны); в) "склейка" решений на участках 2 и 3 позволит найти значение температуры на границе учатков 2—3, а далее последовательно — значения температуры во всех точках участков 2 и 3 (т. к. начальное значение температуры и все прогоночные коэффициенты известны); г) после нахождения температуры на участке 2 находится граничное значение температуры на границе участков 1 и 2 и далее — на всем участке 1. Таким образом, метод обратной прогонки в каждый момент времени позволяет вычислить распределение температуры по всем 3 участкам: "стеклянная стенка (1)"—"водоподобная гелевая среда реакционной камеры (2)"—"стеклянная стенка (3)".

При наличии 2 одинаковых нагревателей на обеих гранях (схема 1) и при одинаковых по толщине и материалу стенках возможно упростить схему расчета: "склеить" 2 решения — на одной из стенок и на половине реакционной камеры. В этом случае целесообразно использовать осевую симметрию и на оси установить граничное условие 2-го рода в форме ∂ Т / ∂ х = 0.

Табл. 2. Зависимость средних температур стенок и реакционной камеры от параметра Δ х конечно-разностной схемы

Δ х , мкм	Температура стенки 1, ºС	Температура гелевой среды, ºС	Температура стенки 2, ºС
6.7	23.418	16.598	14.698
5.0	23.414	16.584	14.691
2.9	23.408	16.566	14.683
2.0	23.406	16.559	14.679
1.7	23.405	16.556	14.678
1.4	23.405	16.554	14.677

Оценка устойчивости расчетов при различных уровнях пространственной дискретизации сетки (расчетные значения температуры при различных Δ х ) иллюстрируется далее данными табл. 2. Время 2.5 с, схема управления температурой 2; в табл. 2 приведены расчеты среднего значения температуры по обеим стеклянным стенкам толщиной 0.2 мм, а также среднее значение температуры гелевой (водоподобной) среды толщиной 0.8 мм.

В целом устойчивость оценок достаточно высока. Однако необходимость "склейки" нескольких решений также накладывает ограничения на величину максимально допустимого Δ х , поскольку приравниваются не только значения температуры, но и величины тепловых потоков, пропорциональные градиенту (первой разности). Таким образом, завышение Δ х должно привести к уменьшению точности оценки потока, и как следствие, всего температурного профиля. Данные в табл. 2 свидетельствуют о стабилизации оценок температуры при Δ x ≤ 2 мкм.

Как говорилось ранее, после завершения первой стадии цикла (линейный нагрев нагревателя) "отставание" средней температуры микрореактора от управляющего (задающего) значения составляет Δ Т = А (12 а ² /l ²)^–1. Если допустить возможность реализации второй стадии цикла (отжиг) при отклонении средней температуры от заданной на 1 град, то в соответствии с (2) можно приближенно оценить помимо времени нагрева 40/ А и время уменьшения отставания температуры до 1 град и менее. Приближенно это время определяется первой постоянной времени и составляет ln( Δ Т )( а ² π ² /l ²)^–1 . На основе данных соотношений можно решить задачу минимизации по параметру А суммарного времени начала стадии отжига, а с учетом того, что собственно время отжига известно, и минимизации суммарного времени двух первых стадий цикла (переход от денатурации к отжигу и сам отжиг).

В наших условиях А орт = 40( а ² π ² /l ²)^–1 ≅ ≅ 62.8 град/с . Очевидно, что такое значение на практике недостижимо, т. е. при данных материалах и размерах микрореактора скорость нагрева должна быть увеличена настолько, насколько позволяют возможности нагревателя . В то же время при увеличении габаритов реакционной камеры (до 4–5 мм и более) оптимальное значение А может оказаться практически достижимым. Тем самым решение указанной задачи оптимизации не будет носить предельный характер, а будет соответствовать определенному нетривиальному режиму работы нагревателя.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ВЫВОДЫ

В заключительной части статьи на основе описанной ранее методики расчетов представлены

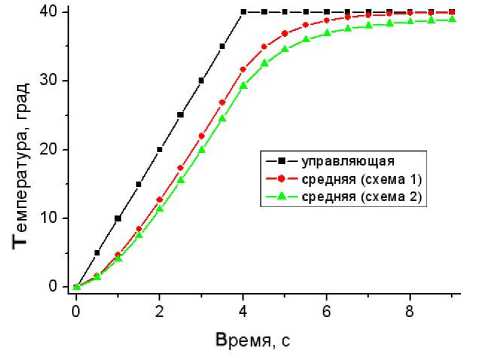
Рис. 6. Зависимость средней температуры реакционной камеры от схемы управления температурой

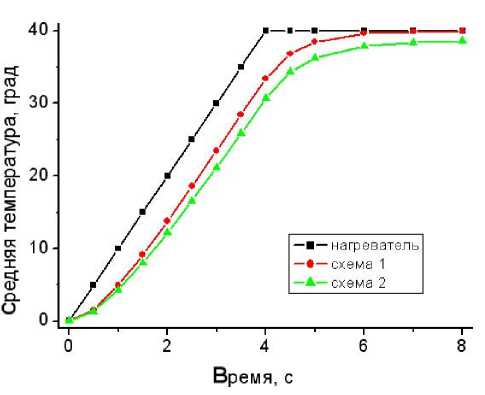
Рис. 7. Зависимость средней температуры от времени оценки влияния алгоритма (схемы) управления температурой, а также геометрических размеров собственно реакционной камеры и стенок на формируемые температурные профили.

Зависимость от выбранной схемы управления нагревом

Зависимость от выбранной схемы управления нагревом представлена на рис. 6. Далее на рис. 7 и 8 приведены расчетные распределения средней и минимальной температур в реакционной камере при различных схемах управления.

Расчеты коэффициентов корреляции между средними и минимальными температурами показывают практически линейный характер их связи. Оценки по четырем методикам — выборочный

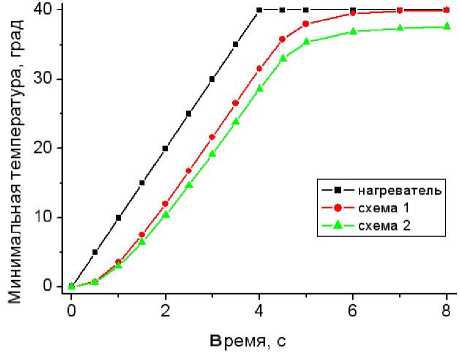
Рис. 8. Зависимость минимальной температуры реакционной камеры от времени

Время, с

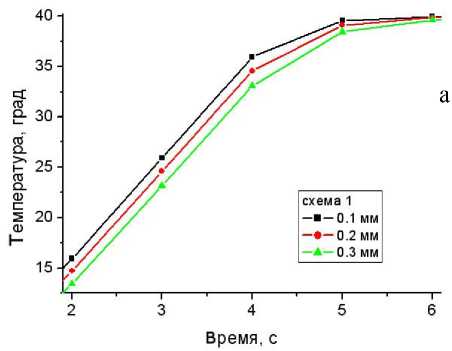
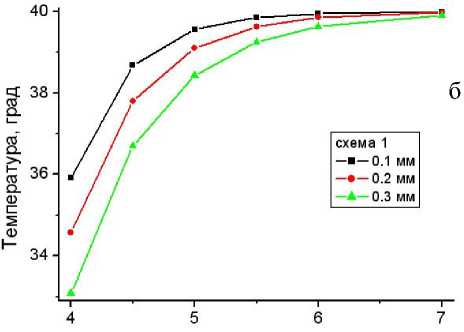
Рис. 9. Зависимость средней температуры реакционной камеры от толщины стеклянной стенки (а). Укрупненный фрагмент зависимости при временах более 4 с, т. е. стадии постоянства температуры нагревателя (б)

коэффициент корреляции (Пирсон) и его медианный аналог (Шевляков), ранговый (Спирмен) и знаковый (Кендалл) коэффициенты корреляции [8] — превосходят 0.996. При этом последние две оценки благодаря строгому возрастанию как средних, так и минимальных температур, очевидно, в точности равны 1.

Зависимости средней температуры реакционной камеры толщиной 0.7 мм от толщины стеклянных стенок

Зависимости средней температуры реакционной камеры толщиной 0.7 мм от толщин стеклянных стенок представлены на рис. 9. Стеклянные стенки имеют толщину 0.1, 0.2 и 0.3 мм. Практически увеличение толщины стенки просто увеличивает термоинерционность объекта. Оптимальное приближение средней температуры реакционной камеры к управляющей температуре нагревателя реализуется при тривиальной конструкции — толщина стенки равна нулю. Т. е. при постоянстве размеров реакционной камеры стенка должна быть настолько тонкой, насколько это позволяют технологические ограничения и условия прочности. Также, согласно рис. 9, б, можно отметить, что во времена 5.5 с и более кривые практически сходятся. Т. е. задержка начала второй стадии (отжига) в этих случаях не превышает 1.5 с.

Анализ влияния асимметрии геометрии

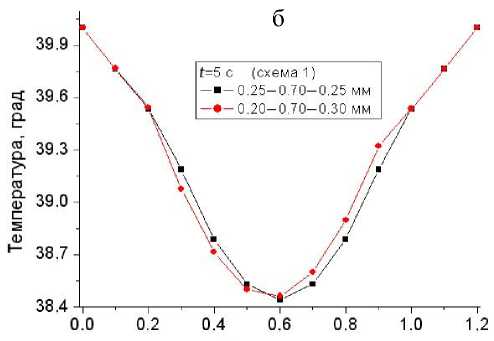
Анализ влияния асимметрии геометрии (различная толщина стенок при симметричном управлении температурой по схеме 1) иллюстрируется рис. 10.

В целом характер обеих зависимостей одинаков. Асимметрия при различных толщинах стенок 0.2 и 0.3 мм по сравнению с симметричным вариантом 0.25 мм, очевидно, объясняется многократно большей термодиффузией стекла по сравнению с гелевой (водоподобной) средой. Однако расхождение кривых и на стадии линейного нагрева (а), и на стадии стабилизации температуры (б) невелико. Таким образом, при изготовлении конструкции нет особо жестких требований по выравниванию толщин стенок.

Зависимость средней температуры реакционной камеры от расположения нагревателя

На рис. 11 сравнивается распределение температур при несимметричной схеме управления (управление температурой по воздушному каналу, или схема 2) для одной геометрической конструкции микрореактора, но при различном расположении нагревателя (на тонкой 0.2 мм или на толстой 0.3 мм стенке).

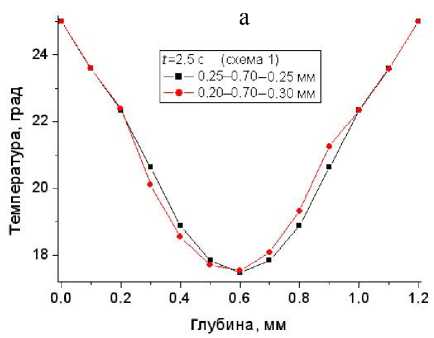
Рис. 10. Температурные профили в моменты времени 2.5 с (а) и 5 с (б)

Глубина, мм

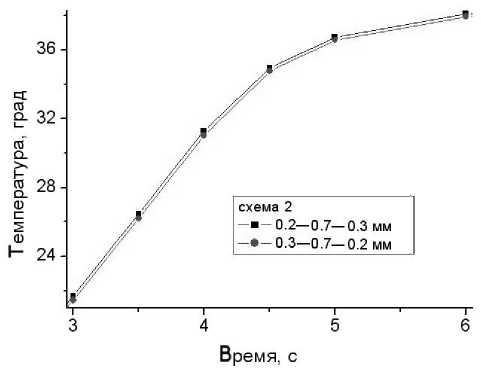
Рис. 11. Зависимость средней температуры реакционной камеры от расположения нагревателя

Видно, что расхождение кривых незначительное. Однако лучшее отслеживание температуры нагревателя обеспечивается при размещении нагревателя на более тонкой стенке.

Рассмотренные в работе принципы температурного управления и найденные основные закономерности позволяют выполнить оценочный расчет временн ы х параметров цикла ПЦР, в том числе и для других аналогичных конструкций реакционной камеры, отличающихся геометрическими размерами и физико-химическими характеристиками используемых материалов.

Уточнения математической модели, а именно учет теплопереноса в горизонтальной плоскости (увеличение пространственной размерности модели), учет утечки тепла через границы термостата, изменение коэффициентов термодиффузии и теп- лообмена с изменением температуры и т. п., не должны принципиально повлиять на основные выявленные закономерности, хотя и приведут к небольшим корректировкам оптимальных алгоритмов управления температурой, минимизирующих время цикла.

В перспективе планируется сопоставить данные оценочные расчеты с натурными экспериментами, после чего возможно внедрение в практику анализа оптимальных алгоритмов температурного управления для повышения производительности ПЦР в реальном времени и повышения быстродействия ММК на микрочипе.

Работа выполненна при поддержке Программ фундаментальных исследований Президиума РАН "Создание и совершенствование методов химического анализа и исследования структуры веществ и материалов" (проект "Микрофлюидные чипы для анализа биополимеров") и "Фундаментальные науки — медицине" (проект "Картриджи-микрочипы для метода молекулярных колоний").