Математическое моделирование деформирования роговицы глаза приложенным извне давлением

Currently, many devices have been developed and are used in the clinic, based on the action of an air jet on the cornea of the eye and designed both for measuring intraocular pressure and for a more detailed study of the mechanical properties of the eyeball. Various deformation characteristics of the cornea are directly measured depending on the set parameters of the jet. In particular, the displacement of the central point of the cornea (apex) under the action of the applied pressure can be determined. In many devices, the pressure in the jet or the duration of its impact, at which flattening of a certain area of the cornea surrounding the apex is achieved, is evaluated. In more subtle studies (for example, in the ORA device [8], which is popular in domestic clinics), the pressure difference corresponding to flattening during rapid loading and unloading (corneal hysteresis) is estimated.

As with other indirect ophthalmological measurements accepted at the clinic, two problems arise. The main thing for medicine is the possibility of using such measurements to diagnose pathologies, primarily glaucoma, and to objectively evaluate the results of treatment.

Irina N. Moiseeva, Ph.D., Senior Researcher, Moscow

Alexander A. Stein, Ph.D., Leading Researcher, Moscow

This problem is solved, first of all, by the accumulation of statistical data. However, a large individual scatter of the mechanical properties of the eye tissues [11] and the geometric characteristics of the eyeball makes it relevant to obtain reliable results when examining a specific patient, which is impossible without solving another problem – a clear assessment of the mechanical meaning of the results. To solve this problem, mathematical modelling of the processes occurring during the measurement is necessary.

Depending on the nature of loading and directly measured characteristics, when studying the mechanics of jet loading of the eye, it may be sufficient to simulate the process either within the framework of a purely elastic model or its generalization taking into account the viscoelastic behavior of the eye tissues. The latter is significant if the measurements (as in ORA) involve obtaining results in a quick-time scanning. We previously developed [9] the most simplified approach to the mechanics of the eyeball, which is characterized by a small number of parameters to be determined and proved to be useful in modelling various types of tonometry. In the framework of this approach, the cornea is represented by a momentless (soft) isotropic homogeneous two-dimensional surface and the scleral region by a zerodimensional element that responds by a change in volume to a change in intraocular pressure. In the basic version, the dependences of the cornea strains on stresses and of the volume of the scleral region on pressure changes were assumed to be linearly elastic. Subsequently, generalizations of the basic model to include the cases of spatially inhomogeneous and nonlinearly elastic corneas were considered [10, 14]. In the present study, we restrict ourselves to linear constitutive relations for the cornea and scleral region, allowing in the general case to take into account their viscoelastic Voigt-type behavior. However, many problems can be investigated on the basis of the purely elastic model.

The mechanical, in particular elastic, properties of the eye tissues are not only highly individual – they are characterized by non-linearity, anisotropy and spatial inhomogeneity. Particularly extensive data have been accumulated from a detailed study of the mechanical properties of the cornea [1, 3, 5, 13]. In the literature, the loading of the eyeball with an air jet is usually modeled, as for other methods of loading it, based on cumbersome finite element models containing many constants [2, 7]. These constants are determined, as a rule, in experiments on cadaveric material with averaging of results over many eyes. When modelling fast unsteady processes that occur during exposure of the cornea to a jet, the data obtained in experiments with significantly longer characteristic times are often used. All these circumstances make it difficult to effectively solve the inverse problem directly for the examined eye.

In recent years, the use of optimization methods based on finite element models to determine unknown parameters has become widespread. This approach has been applied to jet loading of the eye [6]. However, on this path the physical meaning of the relations used is poorly visible, and it turns out that the selection of parameters inaccessible during direct measurements can be carried out within the framework of models that incorrectly takes into account the main features of the mechanical behavior of the object.

A study based on an elementary model with a small set of determining parameters makes it possible to understand the mechanisms of the observed phenomena, find out the physical meaning of the measured quantities, and outline the paths of the minimum necessary generalizations for describing more subtle effects that are not described by this model. This is the advantage of this approach in comparison with computational methods that require a set of characteristics that cannot be reliably evaluated, especially for a particular eye being examined.

Formulation of the problem: equations of equilibrium for the cornea and GEOMETRIC RELATIONS

• Fig. 1 schematically shows an eyeball that is not loaded from the outside ( a ), as well as loaded with external pressure applied in a limited central region of the cornea ( b ).

a                                             b

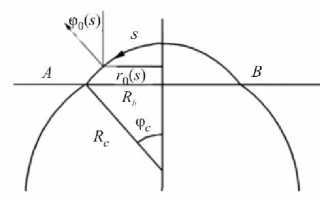
Fig. 1. To the statement of the problem: a – the eyeball before loading; b – the cornea is loaded with external pressure. The plane AB delimits the cornea from the scleral region. Arrows ( b ) indicate the region where external pressure is applied. See text for other designations

Since in the general case it is supposed to consider sufficiently fast processes, it is necessary to evaluate whether it is possible to use static relations in this case, i.e., firstly, neglect the inertial terms in the dynamic equations for ocular tissues and, secondly, not consider non-stationary processes in the liquid. The first is obviously possible if the condition t* >> L(E / p)-1/2 is satisfied, and the second if t* >> LI a, where t* and L are the characteristic time of the process and the characteristic size of the object, respectively, E is the smallest of the characteristic elastic moduli, ρ the characteristic tissue density (almost equal to the density of water), and a the speed of sound in water. Taking L ~1 cm, a ~1500 m/s, E ~0.3 MPa [9], we see that the nonstationarity of processes in the liquid becomes significant for the eyeball at times of the order of microseconds and the nonstationarity for tissues at times less than a millisecond. Since the processes under consideration have a characteristic time of at least tens of milliseconds, both assumptions are satisfied. The assumption of the stationary nature of the fluid redistribution processes is obviously satisfied with very high accuracy, whereas for coat tissues the taking of the non-stationary effects into account could lead to corrections only with accurate calculations, which for the practical study of the processes under consideration do not make sense. On the other hand, at such times, experiments show that the effects of non-instantaneous deformation (Voigt viscoelasticity) become significant [8]. The smallness of fluid displacements caused by external actions during tonometry also allows us to neglect the effects of viscosity of a low-viscosity fluid (essentially water) in the anterior chamber under the cornea and to assume that the pressure is established in it instantly.

Therefore, we will use the static equations for the cornea, which, preserving the assumptions formulated in [9], take in the presence of distributed external pressure, for example, generated by the jet, the following form:

'

• ( Г о тT ) - T ₂ cos Ф = 0,

• -T, sin ф- r ₀ф' T +^ Г ( P — P* ) = 0,

r' = X cos 9,

sr r0 = Rc sin 9o, 9o = —, X = 1 + £1, s 2 =--1-

^Rc                   r 0

Here, r is the distance from the axis to the point at the surface representing the cornea, ф is the angle between the normal to this surface and the axis of symmetry, s the length of the arc of the generatrix that forms the cornea in the initial state, measured from the point of intersection of the cornea with the axis of symmetry (apex) and playing the role of an independent variable, and p the actual intraocular pressure; T and T are tangential forces in the meridional and perpendicular to it (circumferential) directions; E c is the stiffness of the cornea as a surface and v_c is Poisson's ratio; £ and £₂ are the strains in the directions of the main axes, counted from the initial state of the cornea that is not loaded from the outside. The initial state is considered conditionally corresponding to a certain spherical, spatially uniform segment of radius R_c (radius of the cornea), with internal pressure p , which will be further identified with intraocular pressure before loading. Before the start of deformation ( t = 0 ), the forces T_x and T₂ are equal and are determined by the formula T 1 = T ₂ = T _o = p₀R c 1 2 . The radial coordinate and time function p , ( r , t ) >  0 determines the external pressure applied to the cornea. In the case of jet action, this function is nonzero for T₂1 >  0 in a limited area - r <  r <  r , where r j is the radius of the area in which the air stream acts on the cornea. The tangential component of the impact of the jet on the cornea will be neglected in comparison with the normal force provided by external pressure.

Constitutive relations and boundary condition

We now consider the linear constitutive relations for the forces T ₁ and T taking into account the Voigt type viscoelasticity. We remain within the framework of the representation of the cornea, which is basic for our approach, as a two-dimensional, momentless, isotropic, and homogeneous surface. In the framework of this approach, the surface does not resist bending and only strains and stresses in the plane tangent to this surface, which are characterized by tensors of the second rank in two-dimensional space, are significant. In problems for which the condition of axial symmetry is maintained during the deformation, only the components of these tensors are present, which are directed along the main axes corresponding at each point to the meridional and perpendicular to it directions. The strains s, and s₂ introduced above turn out to be the main components of the two-dimensional strain tensor, and the forces T ₁ and T ₂ are the main components of the two-dimensional stress tensor.

We introduce the strain energy W (£j,£₂) and the dissipative function 0 (8,,s₂), which depends on the strain rates g and e₂. Due to the smallness of the strain rates, it is legitimate to identify them with time derivatives of s, and s₂, respectively, no matter partial or substantial. The lack of bending resistance manifests itself in the fact that the parameters responsible for changing the surface curvature are excluded from the number of arguments of these functions. Then, the relationship between stresses and strains is determined by the general formulas

9 W 90   _9 W 90

⁷ i                  I            , V q                  I            .

ds_x 9S,         9s₂   9S₂

Taking into account the isotropy of the corneal material in tangential directions, we will set the strain energy and dissipative function in the form of quadratic functions symmetric in their arguments

x 1 ,   2     1 ,   2,

W (s, , s₇ ) = — k , s, + — k s₇ + k₇ s,s₇ + 7 s, + 7 s₇ ,

12    2  1 1   212    2 1 2    0 1    0

7      1       *2.1       ,2

0(s, , s7 ) = —m s . + —m s 7 + m7 s,s7,

V 1 v  2 z           1  1           12       2  1  2

where the coefficients k , k , m , and m are constants. The dependence of the strain energy and the dissipative function on the principal values of the corresponding tensors ensures the invariance of these dependencies.

Constitutive relations are obtained in the form

I = k Sj + k₂ s₂ + m_x Sj + m ₂ s₂ + 7 , 7 = k s₂ + L, Sj + m, S₂ + m ₂ S| + 7 .

The positive definiteness of the strain energy and the dissipative function leads to the inequalities

k > о, k >| k ₂|, m > o, m > m |.

where

Relations (7) can be transformed as follows:

^S 1 ^+TS ₁ ^+KS 2 = -¹ [ ⁷1 ^-v c⁷ 2 ^{- E}c

7 0, (1 -v . .) ] ,

^S 2 +T^S 2 ^+KS ! = -¹ [ I , ^-v J, ^{- 7}0^{(1 -v} c ) ] , ^Ec

k i - k ₂⁷        k₂        E_c '  _t           e        ^Ec\          ,

E C = ¹ ,  ² , ^v c = T" , ^T = Г^ ^{( m} 1 ^-v c m 2 ) , ^K = Г^ ^{( m} 2 ^-v c ^m 1 ).

^k 1           ^k 1        ^{1 -v} c                   ^{1 -v} c

Obviously, E >  0 and v_c <  1. If we additionally require that v_c >  0 (i.e. k ₇ >  0 , which does not follow from thermodynamic inequalities), then т >  0. The sign of к is not defined, even if additionally requested m ₂ >  0 (by analogy with k ₂). By virtue of (8) and (10), the inequalities

T > | К | > K .

are satisfied.

The coefficients E C and v_c make sense of the elastic moduli (tensile modulus and Poisson's ratio) of the cornea as a two-dimensional elastic surface in slow processes.

We will represent the scleral region with surrounding tissues by a viscoelastic element, the behavior of which is described by the dependence

A V s + t , ( A V_s )^D = K ( p - p ₀),

where A V_s is the increment of the scleral intraocular volume (the part of the internal volume bounded by the sclera and the plane delimiting the sclera from the cornea) due to a change in pressure, and the dot indicates the time derivative. Strictly speaking, generalized relation (12) takes into account not only the viscoelastic behavior of the sclera and surrounding tissues, but also the viscous properties of the medium filling it (the vitreous body), and in a detailed analysis the pressure in this medium can turn out to be not only different from the intraocular pressure p (i.e. the pressure in the anterior chamber), but also spatially inhomogeneous.

The total increment of the volume of fluid in the intraocular space is defined as the sum of A V and the increment of the “sub-corneal” volume A V_c (part of the volume lying above the plane AB ). The increment A V_c is calculated based on the functions r ( s ) and ф( s ) calculated in solving the boundary value problem for the cornea.

In the considered problem, the total increment of the volume is zero due to the possibility of neglecting the inflow and outflow of intraocular fluid during tonometry:

A V = A V +A V = 0.                            (13)

By virtue of symmetry, a solution to the boundary value problem for the cornea is sought in only one half-plane ( 0 <  s <  ф _c R _c ). The condition of fixing the cornea on the plane AB of the outer circle along which it contacts the sclera and the conditions at its intersection with the axis — of collinearity of the axis and the normal and of boundedness of the meridional deformation — are similar to those used in [9]:

r ( ф c R c ) = R b = const,                                     ⁽¹⁴⁾

ф(0) = 0, s ^ 0: r ~ s (1 + £,).

The elastic constants are further re-designated according to the formulas E” = 5Ec and K = (ZEs)-1, where 5 = 0.5 mm is the average normal thickness of the cornea, and Z = 1.44 -10"5 mm-3 [9]. We will call Ec and Es the corneal and scleral stiffnesses, respectively.

The geometric characteristics of the cornea (Fig. 1, a ) are taken equal to R_c = 8 mm and R_b = 5.8 mm, which corresponds to the standard values for the human eye.

Modelling of slow loading by external pressure

The characteristic time for the establishment of deformations is equal to т, since the second characteristic time present in relations (9) | к |< т due to inequalities (11). There are no reliable estimates for this time. The presence of viscoelastic effects under jet loading [8] suggests that for the corresponding processes it has the order of tens of milliseconds. More precisely, the parameter т can be estimated by comparing the simulation results with experimental data. In the present study, relatively slow processes for which the characteristic time t* >> т will be considered. In this case, we can restrict ourselves to the elastic model. In accordance with this, in relations (9) we will assume т = к = 0. Thus, the cornea model studied in this section essentially coincides with the linearly elastic model [9] with the difference only in equation (2) (non-zero pressure p ). If we assume that the scleral volume also has time to be established in the characteristic time of the problem (in relation (12) T << t* and it can be assumed that т = 0 ), the absence of a rigid loading device with its replacement by a non-zero external pressure p remains the only difference from the previous formulation. Next, the tonometric problem for such loading is considered. The change in the geometry of the cornea is being studied. The focus is on the assessment of external pressure leading to a flattening of a corneal region adjacent to the apex (the size of this region is not known in advance and, as a rule, is not monitored in practice). All linear dimensions are further nondimensionalized by the undisturbed radius of the cornea R , according to which the independent variable s varies in the range from 0 to s» « 0.8.

The pressure distribution near the surface of the cornea is determined by the design of the device and the evolution of the jet during its propagation. According to the experimental data for ORA presented in [2], this distribution has the general form shown in Fig. 2.

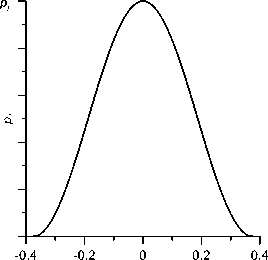
Fig. 2. The dependence of externally applied pressure p on the dimensionless distance to the central axis r accepted in the calculations. When r = 0, the pressure p, reaches its maximum value p„ = Pj

We will be based on the distribution of this type, using the following function to simulate it:

P-Л ^r ) =

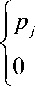
( cos ( n r/r ) + 1 )/2

^{( r} g [ - ^r j , ^r j ^]) ,

(-rj < r < rj), where p is the maximum value of the pressure acting on the cornea, which for definiteness will be called the stream pressure. In what follows, the pressure p will vary, and the halfwidth of the zone of influence of the stream (i.e., the region where p.(r) is positive) is assumed to be 0.385, unless otherwise specified. This value corresponds to the dimensional value given in [2]. The smallness of the deformations and the narrowness of the region of direct jet action make it possible, as necessary, to assume that the dependences p,(r) and p» (5) coincide in the region of action of the stream, as well as to identify the calculated functions of r , characterizing the shape of the cornea in this region, with the corresponding functions of s . The elastic characteristics of the eyeball will vary, but unless otherwise specified, they are assumed to be equal to the characteristics of the “standard” eye: Ec = 0.3 MPa and Es = 10 MPa [9]. The Poisson's ratio in all cases is considered equal to vc = 0.45 .

In Fig. 3, the dependence of the angle φ characterizing the slope of the corneamodelling surface to the central axis is shown for five different pressures in the stream at the same values of elastic constants and true intraocular pressure. It can be seen that at the considered pressures this angle (and, consequently, the shape of the cornea) noticeably changes only in the area of direct action of the jet - r j < r < r j . As p j grows, a region forms in which the cornea becomes concave (i.e., the region of negative φ ). The radius of this region depends on the pressure in the stream and at the stage of its formation, i.e. at pressures not too different from the pressure at which the values ф <  0 appear, it has an order not exceeding r j /2.

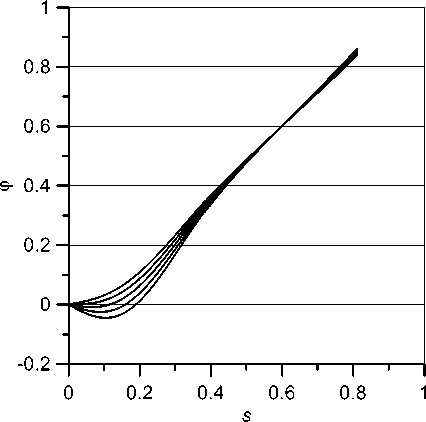
Fig. 3. Dependence of the angle φ on the maximum value of the pressure in the jet for the "standard" eye: p ₀ = 12 mmHg, E_c = 0.3 MPa, E_s = 10 MPa. The values of the pressure in the jet

Pj = 11,13,15,17,19 mm Hg (from top to bottom)

In Fig. 4, the process of indentation of the cornea in the central region is traced at a scale characteristic of this process. Fig. 4, a demonstrates the change of ф ( 5 ) depending on the pressure in the jet, and Fig. 4, b shows the evolution of the shape itself. From Fig. 4, b it can be clearly seen that at a certain pressure p , in fact, there is an almost flat section, which at the calculated values of the parameters approximately corresponds to a pressure of 14 mm Hg and has a half-width 5 ~ 0.1. The graph of ф ( 5 ) (Fig. 4, a ) shows that in this region the angles are close to zero (for 5 <  0.1 the inequality |ф( 5 )| <  0.01 holds).

Strictly speaking, the area where a flat area appears in the cornea does not exist, but visually it is present. In practically used devices, the region of “flattening” is determined by the peak intensity of the light signal reflected from the cornea. The width of the light beam is determined by the design of the device and is usually selected empirically. The calculations we performed in a wide range of physiologically permissible values of the parameters showed that within the framework of the model used, it is advisable to study the flattening process in the region with a dimensionless radius rf * sf ~ 0.1. If this region is chosen substantially narrower, with increasing pressure in the jet the “flattening” zone formed in this region continues to expand to a much larger size. Then, the pressure range corresponding to the “flattening” will be too wide. On the other hand, with a substantially larger radius of the selected region, it will capture the area where the cornea remains noticeably convex at any external pressure, which will significantly distort the overall picture. In what follows, we will always assume that sf = 0.1.

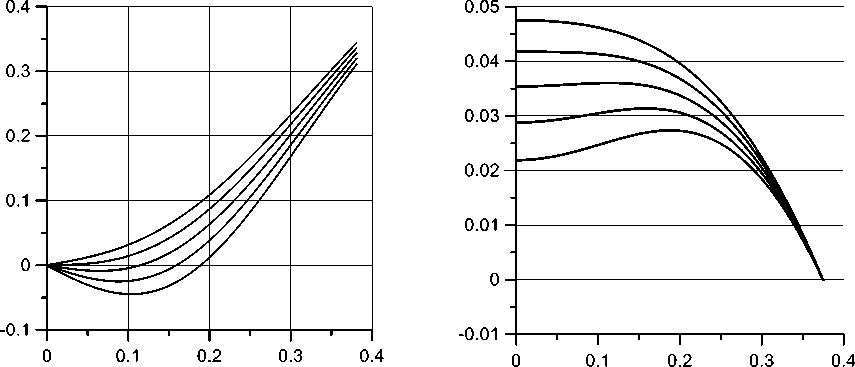
Fig. 4. The distribution of the angle of deviation of the normal to the cornea from the axis ф( s ) ( a ) and the shape of the cornea in the area of influence of the jet ( b ) at pressures Pj = 11,13,15,17,19 mm Hg (from top to bottom). In Fig 4. b , along the axes the distances are indicated in dimensionless units

One cannot speak of the exact pressure value at which “flattening” is achieved, but one can only speak of a pressure range in which the deviation of the normal from the axis is sufficiently small in the area of the chosen radius. This assumption is consistent with the inequality

| ф ( s )| <9 ,                                              (15)

where 9 is chosen sufficiently small, i.e., so that the range of jet pressures in which this inequality holds is sufficiently narrow and acceptable in accordance with the required measurement accuracy. It is also possible to use the criterion sf                                                               (16)

S = ||ф(s)| ds <9.

With an appropriate choice of the constants 9 and 6, both criteria are equivalent. Note that these constants cannot be chosen arbitrarily small, since exact flattening is not achieved.

In what follows, we will choose as the flattening pressure p_jf such a pressure Pj = Pjj at which a minimum of the function S ( p ) is achieved. This approach is convenient in that there is no need to specify the criterion of smallness 9 or 9 , the choice of which is an independent (requiring calculation) problem, since such a criterion cannot be set arbitrarily small.

From Fig. 5, a , it can be directly seen that when choosing s_f = 0.1 the value Pj = p^ at which the minimum of the function S ( Pj ) is achieved can be determined quite clearly: Pj * 13.8 . For such a value of Pj , on the segment 0 <  s <  s^ the angle ф satisfies inequality (16) with 9 = 0.2 x 10 ³. In this case, the flattening pressure p f can be estimated rather roughly: when s changes within a range of width of the order of 1 mm Hg, dependences ф( s ) differ only slightly (Fig. 5, b ). The mentioned circumstance is practically important: it allows us not to require excessive accuracy from the measurement procedure.

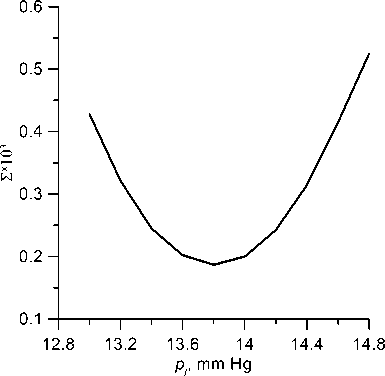
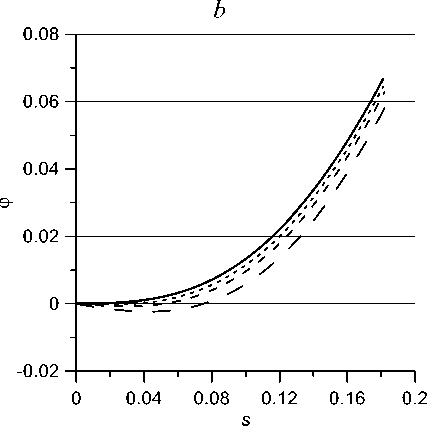
Fig. 5. The calculated graph of the function S ( p _;) ( a ) and the distribution ф( s ) in the region

s <  Tj /2 at Pj = 11,13,15,17,19 (from top to bottom) ( b )

In principle, it is possible not to specify the radius of the region for which flattening is studied in advance, but to seek at each pressure in the jet p the region in which criterion (15) or (16) is satisfied and then find the flattening pressure as such a pressure at which this region is maximally wide. However, the method we used is simpler and, in view of the demonstrated roughness of finding p_jf , will not lead to a significant change in the result. Note that, although the width of the flattening region can be determined within the framework of the model used, in reality (as with Goldmann tonometry) this value strongly depends on the distribution of elastic properties over the cornea thickness and therefore, it is unlikely that it can play the role of a sufficiently effective criterion for the estimation of intraocular pressure.

Fig. 6 shows, with the same parameter values as in the previous calculations, the change, with increasing pressure in the jet, of the distance along the axis from the center point (apex) of the cornea to its border with the sclera, i.e., apex subsidence under the action of the jet. With a uniform increase in the pressure acting on the cornea, the apex sags almost uniformly, but in the pressure region where flattening is achieved, acceleration first and then retardation of the apex sagging can be observed. Upon exiting this pressure range, uniform subsidence resumes. This effect can in principle be used to detect the flattening pressure.

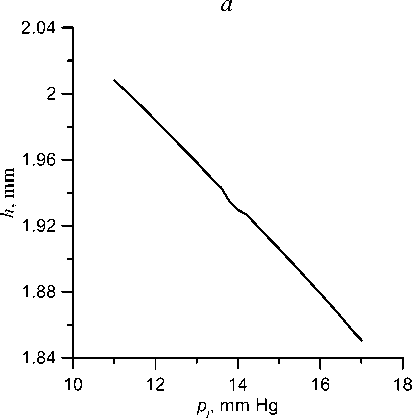
Fig. 6. Dependence (at different scales) of the apex height above the border of the cornea with sclera on the pressure in the jet: а – in a wide range of pressures; b – in the pressure range close to the flattening pressure

Next, we will examine the relationship between the flattening pressure and parameters characterizing the mechanical properties and mechanical condition of the eyeball. Within the framework of the applied model, there are three such parameters: true intraocular pressure p ₀, i.e., pressure in the unloaded eye, as well as the elastic characteristics of the cornea and scleral region E and E .

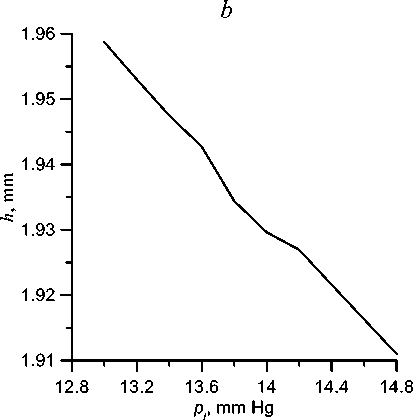
The main task of any tonometry is to determine the true intraocular pressure p ₀. In Fig. 7, the dependence of the flattening pressure on p ₀ is shown. This dependence is close to linear. The flattening pressure p is always greater than p ₀ , and the difference between these values A p increases with pressure: A p ~2 mm Hg at p ₀ = 12 mm Hg and 4 mm Hg at p ₀ = 30 mm Hg. If we estimate the intraocular pressure from the pressure in the jet, assuming the difference between them to be average between these values A p = 3 mm Hg, the error does not exceed 1 mm Hg, which is acceptable for practical purposes. It is more correctly to take into account, in accordance with the dependence presented in Fig. 7, the actual values A p corresponding to different p_j .

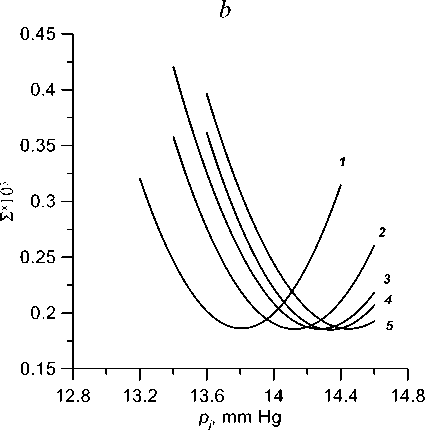
Let us now evaluate the effect on the flattening pressure of the elastic characteristics of the eyeball. In Fig. 8, the dependences S ( p ₇) at significant excesses of normal values, in Fig. 8, a of the corneal stiffness E and in Fig. 8, b of the scleral stiffness, are shown. The minima of the curves correspond to the flattening pressure. With increase in corneal stiffness, the flattening pressure corresponding to the same true pressure decreases, and with increase in scleral stiffness, it increases, i.e., the stiffening of both structures acts, as in the case of Maklakoff tonometry, in opposite directions. In both cases, the difference with the standard eye is small, not exceeding in the considered range of values of the order of 0.5 mm Hg.

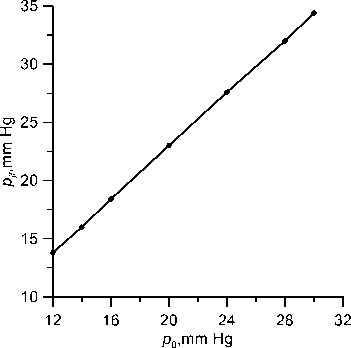
Fig. 7. Dependence of the flattening pressure on the true pressure; E_c = 0.3 MPa, E_s = 10 MPa

Thus, with slow loading by external pressure, the intraocular pressure can be determined with practical accuracy by external action, which leads to a specific deformation (flattening pressure). The individual mechanical properties of the cornea and scleral region, in contrast to static tonometry, affect the relationship between true pressure and flattening pressure only slightly.

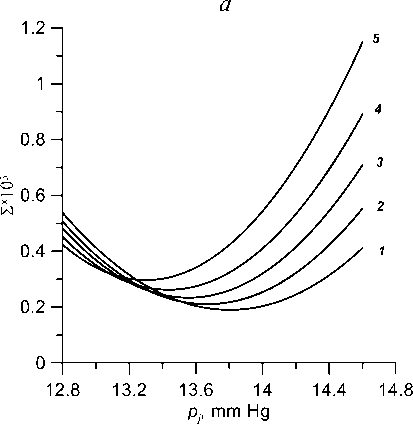
Fig. 8. Function S ( Pj ) at p ₀ = 12 mm Hg and various values of elastic constants: a — E_s = 10 MPa, E_c = 0.3, 0.4, 0.5, 0.6, 0.7 MPa (1-5); b - E_c = 0.3 MPa, E_s = 10, 20, 30, 40, 60 MPa (1-5)

Conclusions

In the framework of our general approach, based on the representation of the cornea as a two-dimensional momentless surface and the scleral region as a zero-dimensional element that responds by volume changes to changes in intraocular pressure, a model has been developed that takes into account the viscoelastic (Voigt-type) properties of eye tissues. The problem of deforming the eyeball under the action of a pressure exerted on the cornea from the outside in a limited area, in particular, due to the action of an air jet, is formulated.

Relatively rough effects appearing under slow loading, when it is possible to neglect the viscosity of the cornea and scleral region, are examined in detail. The model reproduces a 446 ISSN 1812-5123. Russian Journal of Biomechanics. 2019. Vol. 23, No. 4: 435–448

number of the most important features of the jet effect on the cornea of the eye. It is shown that at a certain pressure in the jet, in the central region of the zone of its impact, a section forms, which can be considered as flat with high accuracy. It is the formation of the flattening zone that is monitored by many devices used in medical practice. From the pressure in the jet at which this zone occurs, true intraocular pressure, i.e., pressure in an unloaded eye, can be determined with good accuracy. Of practical importance is the weak influence of the elastic properties of both the cornea and the scleral region on the relationship between these pressures. With a uniform increase in external pressure, in the region of external pressures corresponding to “flattening,” the corneal apex subsidence rate changes: this rate, which is approximately constant outside this region, first increases, then drops, reaching a constant value outside it again.

The above model, which takes into account viscoelasticity, allows one to obtain finer estimates and model the behavior of the eye in high temporal resolution during its rapid loading and unloading. It is the fast processes, for which the effect of viscoelasticity is significant, are realized in most of modern devices that carry out jet action on the cornea. It is easy to show that in this case the model describes the difference between pressures corresponding to flattening in these processes (the so-called corneal hysteresis). The corresponding detailed calculations will be presented in subsequent publications.

Further modification of the model will allow us to take into account the inhomogeneity of the corneal thickness, which, as shown by numerous studies [2, 4, 7, 12], is essential for estimating the real mechanical characteristics of the eye, primarily intraocular pressure, from tonometry data. The first stage of such a study can be the approach developed by us earlier [9], in which the inhomogeneity of the thickness and mechanical properties of the cornea is taken into account through an integral characteristic - effective stiffness. However, the fact that the effect of the jet is mainly concentrated in a rather narrow region (the width of which is comparable to the thickness of the cornea) will most likely require the development of a less rough model that takes into account the inhomogeneity of thickness separately from the inhomogeneity of stiffness.

Acknowledgment

This work was partly supported by the Russian Foundation for Basic Research (project No. 17-01-00380).

Received