Математическое моделирование движения автотранспортных потоков методами механики сплошной среды. Двухполосный транспортный поток: модель Т-образного перекрестка, исследование влияния перестроений транспортных средств на пропускную способность участка магистрали

Первые математические модели движения автотранспортных потоков с точки зрения механики сплошной среды опубликованы Лайтхиллом и Уиземом [1], а также Ричардсом [2]. Анализ основных полученных ими результатов дается в известной монографии Уизема [3]. С развитием вычислительной техники для изучения движения автотранспортных потоков стало широко применяться численное моделирование. С современным состоянием вопроса можно ознакомиться, например, прочитав учебное пособие по математическому моделированию транспортных потоков [4].

Изучение динамики автотранспортных потоков началось в нашей стране в конце 70-х годов XX века на механико-математическом факультете МГУ им. М.В. Ломоносова в связи с подготовкой к Олимпийским играм 1980 г. в Москве. Результаты этих исследований неоднократно докладывались В.Н. Беловым на научно-исследовательском семинаре И.Н. Зверева. В настоящее время изучение автотранспортных потоков на факультете ведется под руководством Н.Н. Смирнова и А.Б. Киселева на кафедре газовой и волновой динамики и в лабораториях волновых процессов и динамики деформируемых сред. Эти исследования неоднократно поддерживались грантами Правительства г. Москвы и Правительства региона г. Брюсселя (Бельгия).

Существуют три традиционных «механических» подхода к моделированию движения транспортного потока. Микроскопические модели описывают воздействие предыдущего автомобиля на следующий за ним при помощи обыкновенных дифференциальных уравнений, основанных на ньютоновской механике [5, 6]. Макроскопические модели основываются на уравнениях газовой динамики [1, 7, 8]. Мезоскопические модели представляют собой промежуточное звено между двумя предыдущими моделями. Они основаны на кинетических уравнениях больцмановского типа [9]. В рамках макроскопического, или континуального, подхода для описания движения потока транспорта используется уравнение неразрывности. В качестве второго уравнения ряд исследователей использовали эмпирическое соотношение, связывающее плотность и расход [2, 10]. Такая система позволяет описывать движение локальноравновесного потока. Для описания неравновесного потока было предложено уравнение движения, учитывающее стремление водителя привести свою скорость в соответствие с некой равновесной скоростью [11]. Однако такой подход не позволяет адекватно описывать возникновение ударных волн плотности потока автомашин. Существующие газодинамические модели не учитывают влияние движения впереди идущих транспортных средств на движение автомобилей, следующих позади, и стремление водителя привести свою скорость в соответствие с максимально безопасной скоростью. На решение этих проблем и направлена предлагаемая модель. Ранее проведенные исследования, использующие ее, опубликованы в работах [12--19].

• II.    Модель движения транспортного потока по автомагистрали

Рассмотрим однонаправленный поток машин по однополосной дороге. Пересечение с другими дорогами и наличие светофоров будет учитываться соответствующими граничными условиями. Введем Эйлерову систему координат x вдоль автомагистрали в направлении движения потока и время t. Среднюю плотность потока р(x,t) определим как отношение площади полосы движения, занятой транспортными средствами, к площади всего рассматриваемого участка полосы движе- ния:

Str hn^ n^

Р = "S = hL = L

где h — ширина полосы движения, L — длина контрольного участка дороги, ^ — средняя длина транспортного средства с минимальным расстоянием между стоящими автомобилями, n —количество транспортных средств на контрольном участке. Так введенная плотность является безразмерной величиной и изменяется в интервале 0 <  р <  1.

Введем скорость потока v ( x,t ), которая может изменяться в пределах 0 ^ v ^ v max , где v max — максимально разрешенная скорость движения на магистрали вне систем регулирования дорожного движения. Из определений следует, что максимальная плотность р = 1 соответствует ситуации, когда машины располагаются практически вплотную («бампер в бампер»). В этом случае естественно принять v = 0, то есть на дороге образовалась «неподвижная пробка».

Условно называя «массой», сосредоточенной на участке длины L , величину

L m=1 *

можно записать закон изменения «массы» на автомагистрали. Для непрерывного потока машин будет иметь место уравнение неразрывности:

^др ₊ ^{д (} pv ) = ₀ ∂t ∂x

Запишем уравнение динамики транспортного потока, точнее, уравнение изменения режима движения. Режим движения транспортных средств на дороге определяется следующими основными факторами: реакцией водителя на изменение дорожной обстановки и предпринимаемыми им активными действиями, откликом транспортного средства на действия водителя и техническими характеристиками транспортных средств. При разработке модели динамики транспортных средств были сделаны следующие основные предположения:

• •    Модель призвана описывать усредненное движение множества транспортных средств, а не движение каждого автомобиля в отдельности. Вследствие этого модель оперирует с усредненными характеристиками транспортных средств, не учитывая индивидуальных различий мощности, инерции, тормозного пути и т.п.

• •    Модель предполагает в среднем адекватную реакцию всех водителей на изменение дорожной обстановки, а именно: предполагается, что, видя красный сигнал светофора или знак ограничения скорости, например, перед «лежачим полицейским», или скопление машин перед ним, водитель замедляет движение до последующей полной остановки или до допустимой скорости, а не продолжает ускоряться, чтобы впоследствии применить режим экстренного торможения.

• •    Предполагается, что подавляющее большинство водителей соблюдают правила дорожного движения, в частности, не превышают максимально допустимого скоростного режима, разрешенного на дороге, и выдерживают безопасный интервал между транспортными средствами в зависимости от скорости движения. Кроме того, движения транспорта задним ходом нет.

Тогда уравнение изменения скорости запишется в следующем виде:

dv dt = a ’

a = max {—a ; min {a+; a'}};

x +Δ

,           (1 — CT)                   V (P) — v

a = sap + ^-д       ap (t,y) dy +------; (3)

x

k2 dp aρ ρ ∂x.

Здесь a — ускорение транспортного потока; a ⁺ — максимально возможное ускорение разгона; a- — ускорение экстренного торможения; величины a ⁺ и a - положительны и определяются техническими характеристиками транспортного средства. Д — «расстояние принятия решения», то есть длина участка магистрали перед участником движения, где находятся транспортные средства, на характер движения которых реагирует рассматриваемое транспортное средство, σ — безразмерный параметр (0 ^ ст ^ 1), характеризующий «вес» локальной ситуации по сравнению с ситуацией на некотором расстоянии впереди автомобиля. Параметр к >  0 является, как было показано в работах [8, 12, 13], скоростью распространения возмущений («скоростью звука») в транспортном потоке. Параметр τ имеет смысл времени задержки, обусловленной конечностью скорости реакции водителя на изменение дорожной обстановки и техническими характеристиками транспортного средства. Этот параметр отвечает за стремление водителя привести скорость автомобиля в соответствие с максимально безопасной скоростью движения V ( р ) для плотности потока р [8, 12, 13]. В зависимости от того, требуется ли для достижения максимальной безопасной скорости V ( р ) притормаживать или разгоняться, значение параметра τ

ТРУДЫ МФТИ. — 2010. — Том 2, № 4 может быть различным:

( т + V(р) < v, 1 тV(р) > v.

Полученная система (5) двух квазилинейных уравнений с неизвестными ρ,v является гиперболической. Условия вдоль характеристик C + и C ^- в плоскости ( x,t ) следующие:

В выражении (3) для ускорения транспортного потока а' первое слагаемое отвечает за влияние на поведение водителя локальной ситуации, второе — за влияние ситуации вперед по потоку, а третье — за стремление водителя привести свою скорость в соответствие с максимально безопасной скоростью. Если принять а = 0, то выражение для ускорения (3) примет следующий вид:

C+ : dx = v + k,pdv = —kdp; C- : dX = v — k,pdv = kdp.

а '

x +Δ

= Д | a p ⁽ ty ) dy ⁺

x

V(Р) - v τ

.

То есть ускорение зависит только от величины ускорения на участке длины Д, где Д — расстояние принятия решения, и от стремления водителя привести свою скорость в соответствие с максимально безопасной скоростью. При а = 1 выражение (3) принимает следующий вид:

а — ap +

V(р) — v

τ

Теперь ускорение зависит от локальной ситуации, а также от третьего слагаемого. Конкретные значения описанных выше параметров, использовавшихся при математическом моделировании, будут приведены ниже.

Таким образом, для описания динамики автотранспортного потока по однополосной дороге из (1) и (2) получается система двух квазилинейных уравнений в частных производных в дивергентной форме:

Полученные выше характеристики несут информацию о дорожной ситуации соответственно по потоку и против него.

Транспортные потоки и существующие системы организации дорожного движения специфичны тем, что распространение информации происходит однонаправлено — навстречу потоку. Тогда для волн, распространяющихся влево, навстречу потоку с постоянными параметрами, имеет место интеграл Римана, полученный из соотношения на характеристике C ^- (6):

v — v 0 = k —. (7)

Скорость v ( р ) определяется из условия зависимости скорости автомобиля v от плотности потока ρ для условий простой волны, возникающей при начале движения потока с места при условиях р о = 1 и v = 0, с учетом ограничения на максимально допустимую скорость движения ( v a v max ) получим выражение для максимально безопасной скорости движения:

V ( р ) = {—k ln p,v < v °_ях: v °,, ,/и ^ v °,,„ }.    (8)

max max     max

∂ρ    ∂ ( ρv )

dt ⁺ Эх, ^О;

∂ ( ρv )      ∂ ( ρv ² )

dt + дх ра.

∂x

где ускорение a определяется тремя последними формулами (3).

II.1. Исследование основных характеристик системы уравнений, предлагаемой для описания транспортного потока

Модель с постоянной скоростью распространения возмущений. Рассмотрим случай, когда параметр k в формулах (3), (4) постоянен и не зависит от скорости и плотности потока. Данная модель обладает высокой степенью точности,

когда скорость потока превосходит скорость распространения возмущений. Рассмотрим случай, когда а = 1, а т = го . Тогда система (4) примет

вид

др + d ( pv ) =0; dt Эх ’

d (Рv) + d (Рv 2) = —к 2 Эр ∂t ∂x         ∂x .

Оценка величины скорости распространения возмущений k сделана в работе [13], исходя из следующих соображений. Пусть, начиная движение из состояния покоя ( v = 0 ,р = 1) и ускоряясь до скорости v _m ⁰ _ax , поток достигает при этом максимально допустимой плотности р * , гарантирующей безопасность движения. Под безопасной плотностью понимается такая плотность, при которой расстояние между машинами не меньше тормозного пути X ( v ). Тогда

р* = (1+ X (vmax)/I) - 1, k = vmax ln-1(1 + X (vmax)/^).

При vmax = 80 км/ч тормозной путь автомобиля типа ВАЗ составляет 45 м, что при средней длине автомобиля (с учетом минимального расстояния между стоящими автомобилями) ^ = 5 м дает скорость распространения слабых возмущений к = 35 км/ч. Для такой величины v°омакси-max мально возможная безопасная плотность потока равна р* = 0,1. Величины максимальных ускорений для автомобилей данного класса составляют а+ = 1,63 м/с2 и а- = 5,5 м/с2.

Оцененная таким образом «скорость звука» k хорошо согласуется с экспериментальными данными, приведенными в работе [20].

Переменная скорость распространения возмущений. Рассмотрим случай, когда параметр k в формулах (3), (4) зависит от скорости

v и плотности потока ρ . Предположим, что транспортному средству требуется время τ _p для реакции на изменение дорожной обстановки впереди по потоку: к = У/т _р , где т _р — время реакции водителя, 1 ' — расстояние между транспортными средствами (рис. 1). По определению плотности У = t/р , следовательно, к = к 1 /р , где к 1 = У/т р .

В предложенной модели предполагается, что v = 0 при р = 1. Таким образом, получаем зависимость для скорости потока:

v = к1

(р—1).

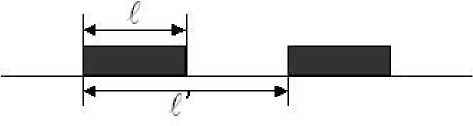
Рис. 1

В модели принимается, что v = к о — к 1 при р = р к . Тогда из (11) получаем следующую зависимость для скорости потока:

v = ко - к1

— к о lnf р) . ρk

Анализ наблюдений за движением потока транспорта показал [20, 3], что при небольшой плотности потока возмущения распространяются с постоянной скоростью. Тогда скорость распространения возмущений можно вычислять по формуле

Г к 1 /р при р >  Р к = к 1 /к 0 , k 0 при ρ<ρ k .

(9)

Учитывая ограничение на максимальную скорость потока ( v < v max ), можно получить следующую зависимость для максимальной безопасной, для данной плотности ρ , скорости потока:

V(р) = min{vmax; кi(1 — 1) при р ^ рл,

ρ

(к о — к 1) — к о ln — при р<рк}.     (12)

ρ k

График этой зависимости представлен на рис. 3.

График этой зависимости представлен на рис. 2.

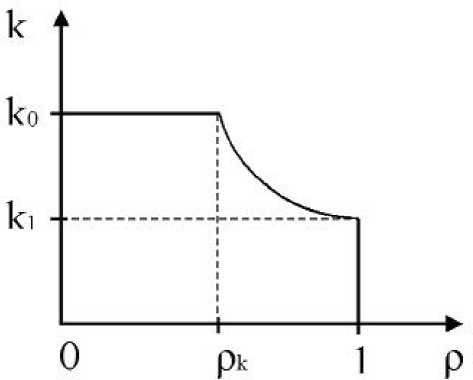
Рис. 2. Зависимость скорости распространения возмущений от плотности потока

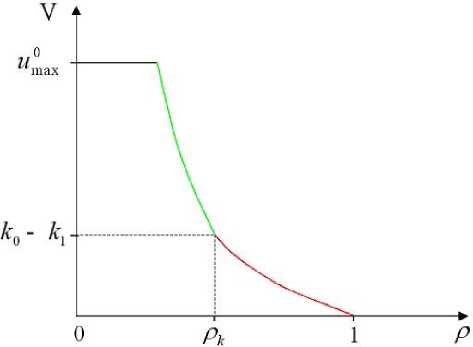
Рис. 3. Максимально безопасная для данной плотности ρ скорость потока

Если в (3) принять о = 1 ,т = го , то при р ^ р к получим систему двух квазилинейных уравнений в частных производных:

др+v др+р dv = о,

∂t ∂x    ρ ₂ ∂x      ,

∂v ∂v k 1 ∂ρ

dt + v Эх + р3 Эх = 0 ■

(10)

Ее характеристики в плоскости ( x ; t )- C + , C и условия вдоль них следующие:

с + : dx = v + р ,р^ = — p йр; C’ : dt = v P ^dv = P dР.

(11)

Для волн, распространяющихся влево, навстречу потоку с постоянными параметрами, имеет место интеграл Римана, полученный из соотношения на характеристике C~ (11):

Экспериментальное определение значения скорости распространения возмущений k 1 при начале движения потока. Эксперимент проводился для однополосного потока машин, без учета возможности перестроений в очереди перед светофором. В начальный момент времени, когда включен красный сигнал светофора, автомобили располагаются вплотную, «бампер в бампер». Тогда, согласно представленной модели, плотность потока р = 1 и к (1) = k j ¹ = к 1 . Величина скорости k 1 определялась экспериментально следующим образом: осуществлялись прямые наблюдения и замеры времени между тем, как загорался зеленый сигнал, и моментами, когда начинали движение автомобили, удаленные на расстояние 1 1 = 48 , 5 ми 1 2 = 73 , 5 м от светофора. Фиксировалось соответственно время начала движения в точках l 1 и l 2 , что позволяло определить среднюю скорость распространения сигнала:

v — v о = к 1

(р a

k 1

1 2 - 1 1

, эксп —

.

t 2 - t 1

Результаты произведенных замеров сведены в табл. 1. В расчетах использовалось среднее арифметическое значение k 1 =4 , 1 м / с ≈ 15 км / ч.

Таблица 1

Результаты эксперимента по определению скорости распространения возмущений k 1

№	l 1 ,м	l 2 ,м	t 1 ,с	t 2 ,с	k 1 , эксп . , м/с
1	48 , 5	73 , 5	14 , 46	19	5 , 5066
2	48 , 5	73 , 5	10 , 99	17	4 , 1597
3	48 , 5	73 , 5	12 , 58	18	4 , 6125
4	48 , 5	73 , 5	9 , 33	17	3 , 2595
5	48 , 5	73 , 5	12 , 53	18	4 , 5704
6	48 , 5	73 , 5	14 , 17	21	3 , 6603
7	48 , 5	73 , 5	11 , 52	19	3 , 3422
8	48 , 5	73 , 5	12 , 5	20	3 , 3333

II.2. Модель перестроений транспортных средств между полосами

Рассмотрим однонаправленный поток машин по двухполосной дороге при подъезде к светофору. Введем эйлерову систему координат x вдоль автомагистрали в направлении движения потока и время t . Средняя плотность потока ρ ( x,t ) вычисляется по формуле (1).

Движение транспортного потока регулируется светофором. L 1 — координата места расположения светофора (рис. 4). Основные параметры работы светофора — длительность сигналов: зеленого t 1 и красного t 2 . Во время работы зеленого сигнала разрешен проезд по обеим полосам, во время работы красного сигнала проезд по обеим полосам запрещен.

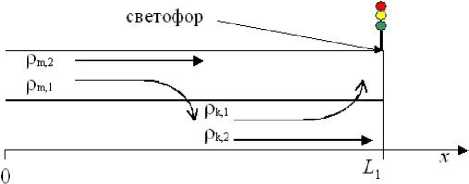
Рис. 4. Схема движения двухполосного транспортного потока с учетом перестроений между соседними полосами

Пусть в начальный момент времени транспортные средства, которые должны проехать светофор в левом и правом рядах, равномерно распределены между полосами движения. Тогда плотность потока по каждой полосе ρ k ( x ) = ρ 1 _,k + ρ 2 _,k , где x — координата вдоль полосы по направлению движения, ρ 1 _,k — плотность транспортных средств, которые не обязаны сворачивать на соседнюю полосу и ρ 2 _,k — плотность тех транспортных средств, что должны перестроится в другой ряд до светофора (рис. 4).

Тогда уравнения баланса транспортных средств на двух соседних полосах с индексами k,m запишутся в следующем виде:

∂ρ 1 ,k ∂t	:      ∂ + ∂x ( ρ 1 ,k v k )=	ω km ( ρ 2 ,m ,ρ k ) ,
∂ρ 2 ,k ∂t	∂ + ∂x ( ρ 2 ,k v k )=	-ω mk ( ρ 2 ,k ,ρ m );
∂ρ 1 ,m ∂t	∂ + ∂x ( ρ 1 ,m v m )	ω mk ( ρ 2 ,k ,ρ m ) ,
∂ρ 2 ,m ∂t	∂ + ∂x ( ρ 2 ,m v m ) =	-ω km ( ρ 2 ,m ,ρ k )

Здесь ω _mk — поток транспорта с полосы k на полосу m . Он рассчитывается следующим образом: рассматривается условие перестроения по близости светофора; если

vkτtr +Δtr >L1 - x, (13)

то необходимо перестраиваться. Рассматривается условие по плотности до светофора (если первое условие не выполнено); если

ρk(L1 >x1 >x) > ρtr, (14)

то производится перестроение. В случае выполнения условия перестроения рассчитывается ω _mk :

(ρ2,k (1 - ρm))δtr ωmk =                ,

τ tr

τ _tr — характерное время перестроения, Δ _tr —дополнительная дистанция, ρ _tr – критическая плотность на полосе, на которую должно быть выполнено перестроение, параметр δ _tr отвечает за интенсивность потока, L 1 — координата светофора.

Уравнения изменения скорости для транспортных средств, движущихся по соседним полосам, запишутся в следующем виде:

dvk = -    k2     ∂(ρ1,k + ρ2,k)

dt ρ1,k + ρ2,k       ∂x ;

dvm = -     k2     ∂(ρ1,m + ρ2,m)

dt      ρ1,m + ρ2,m       ∂x .

Предложенная модель движения двухполосного транспортного потока с учетом межрядовых перестроений при подъезде к светофору учитывает как случай свободного движения потока транспорта, так и ситуацию, когда возникает подвижная пробка.

• III.    Двухполосный транспортный поток

  • III.1.    Математическая модель двухполосного транспортного потока

Рассмотрим однонаправленный поток машин по двухполосной дороге. Введем эйлерову систему координат x вдоль автомагистрали в направлении движения потока и время t . Средняя плотность потока ρ ( x,t ) вычисляется по формуле (1). Для описания динамики автотранспортного потока получается система двух квазилинейных уравнений в частных производных в дивергентной форме (4).

Воспользуемся моделью, предложенной в разделе II.1, то есть будем считать, что параметр k зависит от ρ и эта зависимость выражается формулой (8). Тогда система (4) примет вид (10). В этом случае максимально безопасная скорость движения транспортного потока для данной плотности V ( р ) вычисляется по формуле (9).

В качестве начальных условий примем, что на участке длиной x о , считая от входа x = 0, магистраль занята потоком машин плотности ρ 0 , движущихся с максимально безопасной для данной плотности скоростью V ( р 0 ), а при x 0 < x <  L 1 магистраль свободна от машин ( р = 0 ,v = 0). Плотности транспортных средств на полосах в начальный момент времени вычисляются по следующим формулам:

0             p          0 p

р 1 >* = к1 “ 100 7р0, р2>* = 100р0’

0 p        0             p

• ^р 1 ^,т    100 ^Р 0 ^{, Р} 2 ^,т     1   100 ^Р 0 ^,

где p — процент транспортных средств, которые должны оказаться на правой полосе k до светофора (рис. 4).

В качестве граничных условий на концах рассматриваемого участка магистрали 0 ^ x ^ L выберем следующие: на входе потока при x = 0 возможны два варианта граничного условия.

• 1.    В условиях отсутствия «пробки» задается плотность потока и скорость, равная максимально безопасной для данной плотности:

На основе описанной выше модели двухполосного потока проведено численное моделирование Т-образного перекрестка, образованного примыканием второстепенной двухполосной дороги к основной также двухполосной трассе. Движение на этом перекрестке регулируется светофором с тремя фазами работы. В ходе соответствующей фазы движение на перекрестке осуществляется так, как показано на рис. 5, 6, 7. На рис. 5 видно, что с второстепенной дороги правый поворот осуществим только из правого ряда, а левый — только из левого. На рис. 6 показано, что при движении по основной дороге слева направо правый ряд предназначен для поворота направо, а левый — для движения прямо. При движении справа налево левый поворот осуществляется из левого ряда, а движение прямо — из правого ряда.

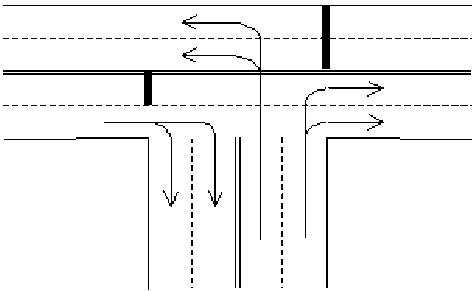
Рис. 5. Схема движения автотранспорта по Т-образному перекрестку в ходе первой фазы работы светофора

Р (0 ,t )= ро; v (0 ,t ) = V (ро).

• 1. В условиях подвижной или неподвижной «пробки», примыкающей к входному участку дороги x = 0, ставится условие равенства нулю градиента плотности, а скорость равна максимально безопасной для данной плотности:

  ∂ρ ∂x

  
  
  

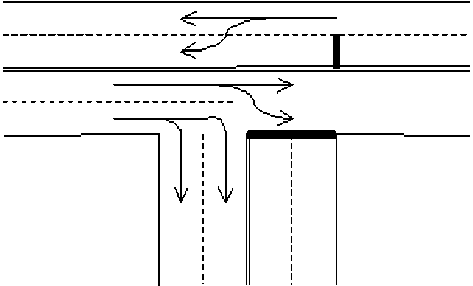
  Рис. 6. Схема движения автотранспорта по Т-образному перекрестку в ходе второй фазы работы светофора

  
  

= 0;   v (0 ,t ) = V (р).

=0

Наличие или отсутствие «подвижной пробки», примыкающей к левой границе расчетной области x = 0, определяется после расчета очередного шага по времени по следующему критерию. Если

∂ρ ∂x

> 0

x =0

и ρ>ρ0,

то имеется «подвижная пробка».

На выходе потока при x = L ставится условие «свободного выхода»:

др = 0; ∂x

5v = 0. ∂x

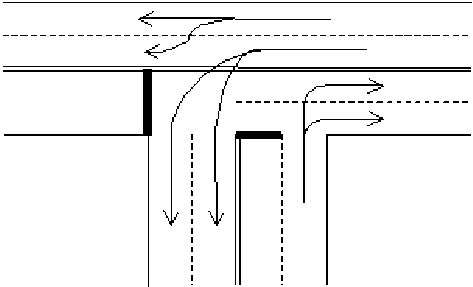
Рис. 7. Схема движения автотранспорта по Т-образному перекрестку в ходе третьей фазы работы светофора

III.2. Модель Т-образного перекрестка

В начальный момент времени автомобили, которые собираются поворачивать или продолжать движение прямо, равномерно рассредоточены по обоим рядам. По мере приближения к светофору автомобили начинают перестраиваться в нужный ряд, если выполнено одно из условий (13) или (14).

При расчетах использованы следующие параметры, общие для трех ветвей перекрестка:

• L 1 = 1000 м — длина участка дороги до перекрестка;

• x 0 =25м — длина участка, занятого движущимся транспортом в начальный момент времени t =0;

• v _m ⁰ _ax =18 м / с — максимальная скорость движения на основном участке дороги;

• v p =3 м / с — максимальная скорость автомобилей, поворачивающих в зоне перекрестка;

• k 0 =7 , 9 м / с, k 1 =4 , 1 м / с — коэффициенты в выражении (2.2.4) для скорости распространения возмущений в потоке автотранспорта;

• a ⁺ =1 , 5 м / с ² — максимальное ускорение потока; a ^- = 5 м / с ² — максимальное (экстренное) ускорение торможения потока;

• a r =1 , 5 м / с ² — стандартное ускорение торможения;

Δ=50м — расстояние принятия решения;

• σ =0 , 5 — «вес» локальной ситуации;

• τ ⁺ =3 , 3 с, τ ^- = ∞ — время задержки подстройки под безопасную скорость движения в выражении (2.1.3);

• ρ _tr =0 , 8 — критическая плотность на полосе, на которую должно быть выполнено перестроение;

• τ tr =5 с — характерное время перестроения;

Δ _tr =20м — дополнительная дистанция; δ _tr = 0 , 01 в выражении (2.5.3); t 1 =60 c , t 2 =45 c , t 3 =5 с — длительности фаз работы светофора;

• ρ ¹ ₀ = 0 , 07, ρ ² ₀ = 0 , 08, ρ ³ ₀ = 0 , 11 — плотности потока автотранспорта на входе в расчетную область при x =0для левой, правой и нижней частей перекрестка соответственно;

p ¹ ₀ = 0 , 26, p ² ₀ = 0 , 65, p ³ ₀ = 0 , 53 — доля транспортных средств, которые должны пересечь перекресток в правом ряду для левой, правой и нижней частей перекрестка соответственно.

На рис. 8 представлены результаты численного моделирования движения потока транспорта через Т-образный перекресток, регулируемый светофором. Здесь изображена плотность потоков транспорта в районе Т-образного перекрестка в моменты времени, обозначенные на рисунке. Шкала соответствия цвета значению плотности транспортного потока приведена в правом углу рисунка. В левом углу изображен график зависимости плотности потока от координаты расчетной области в левом ряду левой части перекрестка при движении слева направо, ось направлена по ходу движения транспортного потока. Момент времени t = 412 с соответствует первой фазе работы светофора, во время которой для левого ряда левой вет- ви перекрестка работает запрещающий сигнал. На графике видно, что в ходе работы запрещающего сигнала начинает образовываться второй участок повышенной плотности. Момент времени t = 465 с соответствует второй фазе работы светофора, в ходе которой включен сигнал, разрешающий проезд перекрестка по рассматриваемому участку магистрали. На графике изображено, что к этому моменту два участка повышенной плотности объединились в один затор, распространяющийся навстречу потоку. Момент времени t = 482 с соответствует третьей фазе работы светофора, в ходе которой проезд перекрестка по рассматриваемой полосе запрещен. График показывает, что у перекрестка вновь начинает образовываться очередь из автомобилей. Поскольку предыдущий участок повышенной плотности за время работы разрешающего сигнала не успел миновать перекресток, то с течением времени затор, образующийся перед светофором, растет. Следовательно, для данного режима работы светофора ρ10 = 0,07 превышает ρ∗0 , максимальную плотность входящего потока, не приводящую к затору.

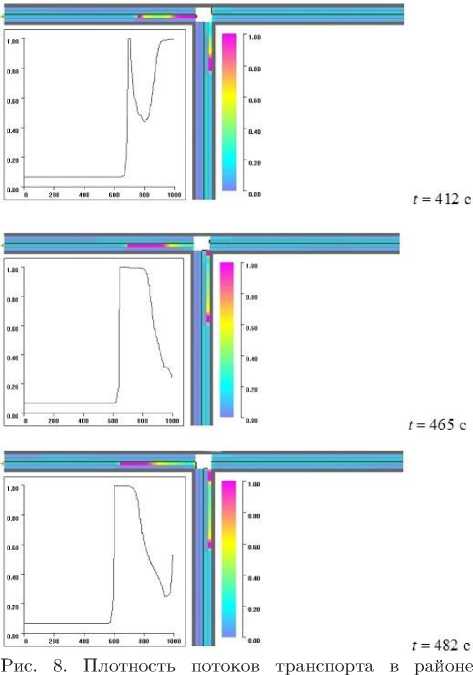
Т-образного перекрестка в моменты времени, обозна- ченные на рисунке

• III.3. Влияние перестроений транспортных средств из ряда в ряд на пропускную способность участка магистрали

Построенная модель движения транспортного потока через Т-образный перекресток использована для изучения влияния межрядовых перестроений на пропускную способность магистрали. Для этого нижняя ветвь перекрестка рассматривалась изолированно от остальной части, а максимальная скорость поворачивающих транспортных средств принималась равной максимально разрешенной скорости на данном участке магистрали v p = v m⁰ ax .

Численное решение поставленной задачи осуществлялось методом TVD со вторым порядком точности [21]. Число узлов расчетной сетки N = 200.

При расчетах использованы следующие параметры:

• L 1 = 1000 м — длина расчетной области;

• x 0 =25м — длина участка, занятого движущимся транспортом в начальный момент времени t =0;

• ρ 0 = 0 . 04 div 0 . 2 — плотность потока автотранспорта на входе в расчетную область при x =0;

• v _m ⁰ _ax =18 м / с — максимальная скорость движения на рассматриваемом участке дороги;

k 0 =7 , 9 м / с, k 1 =4 , 1 м / с — коэффициенты в формуле (9) для скорости распространения возмущений в потоке автотранспорта;

• a ⁺ =1 , 5 м / с ² — максимальное ускорение потока; a ^- = 5 м / с ² — максимальное (экстренное) ускорение торможения потока;

• a r =1 , 5 м / с ² — стандартное ускорение торможения;

Δ=50м — расстояние принятия решения;

• σ =0 , 5 — «вес» локальной ситуации;

• τ ⁺ =3 , 3 с, τ ^- = ∞ — время задержки подстройки под безопасную скорость движения в выражении (3);

• t g = 40 div 350 с, t _r =50с — длительности разрешающего и запрещающего сигналов светофора;

• ρ _tr =0 , 8 — критическая плотность на полосе, на которую должно быть выполнено перестроение;

• τ tr =5 с — характерное время перестроения;

Δ _tr =20м — дополнительная дистанция; δ _tr = 0 , 01 в выражении (15).

В расчетах варьировалась плотность входящего потока ρ 0 (а значит, и его скорость) и длительность работы зеленого сигнала светофора t g .

Результаты расчетов представлены на рис. 9, 10, 11, 12, 13, 14, 15 и в табл. 2.

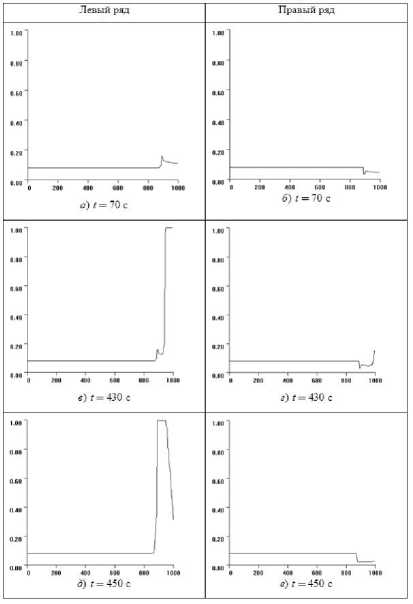
Рис. 9. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени для случая отсутствия подвижной пробки

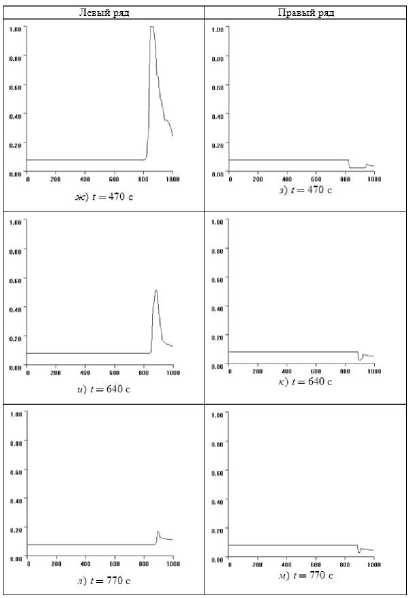
Рис. 10. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени для случая отсутствия подвижной пробки

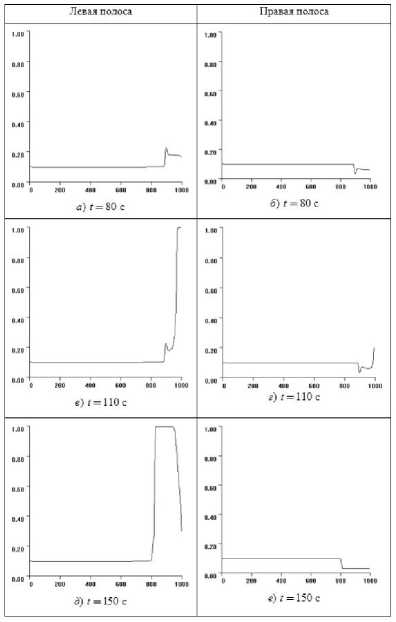
Рис. 11. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени для случая возникновения подвижной пробки

Рис. 13. Шкала соответствия цвета значению плотно- сти транспортного потока

Рис. 14. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени для случая отсутствия подвижной пробки. Движение транспортного потока происходит слева направо

Рис. 15. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени в случае возникновения подвижной пробки. Движение транспортного потока происходит слева направо

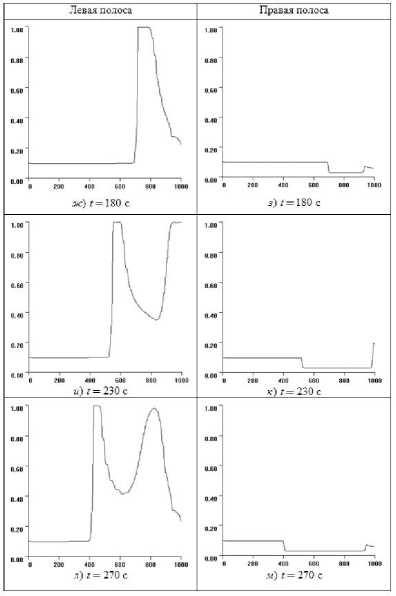
Рис. 12. Распределения плотностей ρ m и ρ k в левой и правой полосах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени для случая возникновения подвижной пробки

На рис. 9, 10 и 14 даны распределения плотностей ρm и ρk в левом и правом рядах транспортного потока в зависимости от координаты расчетной области x в различные моменты времени, указанные на рисунке. При этом длительность работы зеленого сигнала светофора tg = 350 с, p = 0,3, а начальная плотность транспортного потока равна ρ0 = 0,08. В начальный момент времени работает красный сигнал светофора и до окончания его работы остается 40 с. При таких начальных условиях поток транспорта движется без образования «подвижной пробки». Время на рис. 9, 10 и 14 соответствует следующим моментам цикла работы светофора: t =70с — зеленый период первого цикла; t = 430 с — красный период второго цикла; t = 450--770 с — 4 последовательных момента зеленого периода второго цикла. Как видно из этих графиков, при t =70с в левом ряду появляется участок повышенной плотности, а в правом пониженной, вызванные перестроениями из ряда в ряд, после включения красного сигнала плотность в обоих рядах повышается. В левом ряду плотность повышается до своего максимального значения и образуется неподвижная пробка, но за время работы зеленого сигнала зависимость плотности от координаты x возвращается к своему первоначальному виду, что видно на рис. 12л, м. В этом случае «подвижная пробка» с течением времени не образуется. Возвращение профиля плотности к своему первоначальному виду служит критерием свободного движения потока без образования «подвижной пробки».

На рис. 11, 12, 15 приведены данные для длительности работы зеленого сигнала светофора t g = 50 с, p = 0 , 3 и начальной плотности р о = 0 , 1. В начальный момент времени работает красный сигнал светофора и до окончания его работы остается 40 с. Время на рис. 11, 12, 15 соответствует следующим моментам цикла работы светофора: t = 80 с — зеленый период первого цикла; t =110 с — красный период второго цикла; t = 150 си t = 180 с — зеленый период второго цикла; t = 230 с — красный период третьего цикла; t = 270 с — зеленый период третьего цикла. На рис. 12ж видно, что за время работы зеленого сигнала профиль плотности не успевает вернуться к своему первоначальному виду, и с течением времени в левом ряду образуются участки повышенной плотности, где скорость движения заметно уменьшается. Другими словами, возникает затор, перемещающийся против потока. При этом в правом ряду образуется зона пониженной плотности (рис. 12е, з, к, м). Снижение плотности обусловлено тем, что в левом ряду, в который необходимо выполнить перестроение, плотность превысила критическое значение p tr = 0 , 8 и автомобили начинают перестраиваться в левый ряд задолго до светофора.

Результаты исследования зависимости величины предельной начальной плотности потока р00, при которой не образуется «подвижная пробка», от длительности зеленого сигнала светофора tg и p приведены в табл. 2. Остальные исходные параметры фиксированы. Зависимость р00 от tg хорошо описывается формулой р0 = a ln( tg)+ b, (16) где a, b — параметры, зависящие от многих факторов, включая длительность красного сигнала tr. Для рассмотренных исходных данных значения a, b также приведены в табл. 2, соответствующие графики изображены на рис. 16.

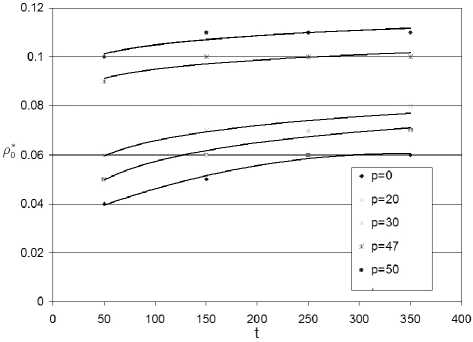
Рис. 16. Зависимость величины предельной начальной плотности потока ρ ^∗ ₀ , при которой не образуется «подвижная пробка», от длительности зеленого сигнала светофора t g и p

Проведенные расчеты позволяют сделать вывод, что предельная начальная плотность потока не зависит от процента машин, которые должны проехать перекресток в левом ряду, что объясняется тем, что совокупное количество автомобилей, выполняющих перестроение, не зависит от этого процента. Однако в целом перестроения снижают пропускную способность магистрали в 2 раза по сравнению со случаем отсутствия перестроений.

Таблица 2

Зависимость величины предельной начальной плотности потока ρ^∗ ₀ , при которой не образуется «подвижная пробка», от длительности зеленого сигнала светофора tg и p , а также соответствующие значения коэффициентов a и b в формуле (16)

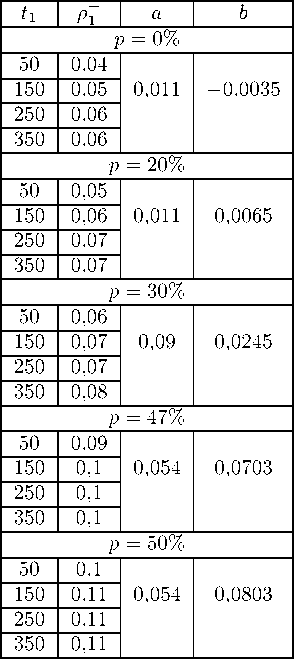
В результате численного решения рассмотренных выше задач получены следующие основные результаты:

• •    Для двухполосного транспортного потока построены зависимости предельной начальной плотности, не приводящей к затору, от длительности зеленого сигнала светофора и от процента автомобилей, меняющих полосу движения.

• •    Установлено, что при регулировании движения двухполосного потока транспорта све-

• тофором максимальная пропускная способность магистрали падает почти вдвое по сравнению со случаем отсутствия перестроений. В связи с этим на особо загруженных участках дорог целесообразно ограничить в целях повышения пропускной способности магистрали возможность перестроений.