Математическое моделирование движения горизонтального решета для разделения кедрового вороха

Введение. В лесном хозяйстве широко используются решета различных конструкций для очистки семенных материалов сосны сибирской кедровой. Наиболее распространены решета, установленные с наклоном, применение данных решет приводит к потерям части семенного материала. Рабочий процесс на решетных станах слагается из ряда составляющих: 1) перемещение решета; 2) движение слоя кедрового вороха по поверхности решета; 3) проникновение частиц сквозь отверстия решета; 4) сход шелухи с решета. Для снижения потерь при просеивании возникла необходимость разработать математическую модель движения горизонтального решета, которая учитывала бы все желаемые качества проектируемого оборудования. Математическая модель составляет основу расчета и оптимизации процесса просеивания. Математическое моделирование движения горизонтального решета обусловлено необходимостью улучшения процесса разделения и снижения потерь семенного материала при просеивании [1]. Установленную зависимость можно использовать для обоснования конструктивных параметров при создании просеивающего оборудования.

Цель исследования : обоснование принципов и методов очистки семенных материалов сосны сибирской кедровой в лесном хозяйстве на горизонтальных решетах.

Для достижения поставленной цели необходимо решить следующую задачу : разработать математическую модель движения горизонтального решета для разделения кедрового вороха.

Методы и результаты исследования . Основное необходимое условие для выполнения поставленной задачи – это неодинаковое перемещение вперед – назад колеблющегося решета. Если удаляемый ворох отходов (шелуха) должен удаляться вправо относительно колеблющегося (вправо – влево) решета, то решето должно перемещаться вправо с ускорением и скоростью значительно меньшим, чем при перемещении влево [2, 3].

Предположения о движении решета:

• 1.    Поступательно-возвратное движение вдоль одной прямой с обязательным возвращением в исходную точку. Решето движется как абсолютно твердое тело, т. е. все его точки в рассматриваемой задаче движутся одинаково, движение периодично.

• 2.    Отношение времени движения туда и обратно всегда одинаково (в данной задаче оно равно двум).

• 3.    Движение решета при разгоне и торможении моделируется как движение равноускоренное и равнозамедленное соответственно.

Все движения рассматриваем относительно Земли (инерциальная система отсчета).

V1X а1 X т

T1

2 V 1 X T 1

= ² • V = a l ,

T1

а 2 X

—a

• 1 X =

- 2

•

V 1

T 1

^{- a} 1 ,

где Т 1 – первая доля полного периода, с;

Т

• ¹ – вторая доля полного периода, с;

• V 1 – максимальная (по абсолютной величине) скорость решета, м/с;

• 2V 1 – максимальная скорость при перемещении влево, м/с;

• V 1x – проекция максимальной скорости при движении решета вправо (рис. 1).

Далее – повторы (из–за периодичности):

a 5 X    a l X ^,

a 6 X	= a 2 X ,	(4)
a 7 X	= a 3 X ,	(5)
a 8 X	= a 4 X .	(6)

$ 5 X

t           2V

= 0 + I a_5Xdt = —¹ 1 T

3                    1

2T12

= t - 3 V. . (15)

^T 1          ¹

В частности, на концах интервала:

Теперь исследуем проекцию скорости решета (см. рис. 1) на соответствующих этапах.

Начальное условие: <91х   = 0, t=0

$ _5X I

5X t=3 T

= O; ^ I = V , t = 2 T

$  = 0 + [a,di, = f 2Vdt = V t\ = Vt.(7)

1X1X

0         0 T1        T1   0

В частности, на концах интервала:

9„| = 0;$K| = V,(8)

t=0

$  = V + \a_2Xdt = V + ( - 2 V ¹) t\ = 2 V - 2 V • t . ⁽⁹⁾

2X      1        2X         11

T1                      T1 T1

$ 6 X = V . + f a 6 X d = V .

2 T ₁

V

- ² T^ t ⁺ 4 V ■ = (17)

В частности, на концах интервала:

$2x1   = V,;$2xl = 0,(10)

_t = Tt

$ = 0 +{a^dt = —8VV t = -8Vt + 8V = 8V -8V■ t.(11) 3X            3X                                    11

T             T1 T1        T1

В частности, на концах интервала:

$ зх I = 0; $ I  =- 2 V ,

3X             3X                1

t = ^{T l}              t = 5 t

tt

$ = — 2V + f a,_xdt = - 2 V + 8 1 t =

4X          1         4 X            1

T 5

⁵4^T 1                             ¹ 4 ^{T 1} . (13)

= - 2 V + 8 - 1 1 - 10 V =- 12 V + 8 V ¹ • t . 1 _T 1          1 _T

В частности, на концах интервала:

$4X  | t 4 T

=- 2 V ; $ 4x I = 0 . t = 3 T

= 5 V - 2^ • t . ¹       T 1

В частности, на концах интервала:

$ 6X I = V ; « « I = 0 , t = ^2Ti                t = 5 t

$ 7 X

t

= 0 + f a^dt = —i ⁵ ₂ T 1

8 ^{V 1} t^t

T 1   5 T

= 8 t + 20 V = 20 V

T. 1            1

- Vt . (19)

T 1

В частности, на концах интервала:

$7X I = 0;$   |   =—2V, t=5T            t=11 T

2 ¹                      4¹

tt

= —2V + f a8Xdt = —2V + 8 -11\=

11                         T111

4 T1

= — 24 V + 8 V ¹ • t .

$ x

8X

— 2 V + 8 V t — 22 V = (21)

В частности, на концах интервала:

$ 8X I

8X 11

t = 4 ^T

- 2 V ; $ 8x I = 0 .

t = 3 T

Теперь исследуем проекцию перемещения решета на соответствующих этапах (рис. 3)

(начальное условие S1X |  = 0), имеем t=0

Далее – повторы ( t ^ t + 3 T 1 ):

(из-за периодичности)

5 _И = 0 + j $ dt = j 2 V tdt = V t² | t =

1 X        ₀   1 X      _{0 T 1        T 1    0}

^{V 1} t ².    (23)

T 1

В частности, на концах интервала:

S ix I = 0; S ix I = 1 VT ,        (24)

t = 0           /=T    ⁴

S» = ¹ VT + f A dt = ¹ VT + [^f 5 V - 2 ^V • 1 1 dt = ¹ VT +^f 5 Vt - ^V t ²¹ I t = ( ³³⁾ 6X /1 1 1 J    6 X         /1   1 1 J I 1 T I /111 I 1 T I'

⁴       2 T ,          ⁴       2 ? A        T J     ⁴       3       T J 2 T

1                V .                        23                V. .

= - VT + 5 Vt - у t ² - 10 VT + 4 VT = - j VT + 5 Vt - ⁷t ².

В частности, на концах интервала:

s_k = 1 vt + f % dt = 1 vt + f^f 2 v - ^{2 1} 1 1= ¹ vt +[ 2 v • t - Vt- 'll = (25)

^2X 4  ^{1 1} J ² X 4  ^{1  1} J 3    ¹ T 1    4  ^{1 1}    3    ¹         T 1 T

= 1VT + 2Vt - V- - VT +1VT =-1VT + 2V,t - V-, 11       1               11        11          11       1

В частности, на концах интервала:

S.    =1VT;S.    =1VT.(26)

t=T   4          t=t

S

6X t=2 J

= ¹ VT ; s _Sx I = ¹ VT ,

⁴           t . 5 t   ²

t

S_7X = -VT + f A dt . = 7X         1 1         7 X

²          ₂ ⁵ T 1

¹ VT + f I 20 V - 8 ⁷1 1 dt = ¹ VT +| 20 Vt - 4 ⁷1 ² | 2 11           1                  11        1

T       2                T 5

5 T ^{3               1 J                  3                1 J} 2 ■

1                                    .           49       .. 4K ,

= -VT + 20 V,t - 4^ t ² - 50 VT + 25 VT = -y VT + 20 V,t - yr1 ² .

S 3X = 1 VT +b x d = 1 VT1 + J f s v - 8Vt"dt = 1 Vj +f 8 V • t - 4V.t ² 1' = (27) = 1 VT + 8 Vt - 4 ^{V 1} 1 ² - ( 8 VT - 4 VT ) = - 7 VT + 8 Vt - 4 V ¹ 1 ² .

В частности, на концах интервала:

В частности, на концах интервала:

S7X |   = — VT1; S7X |   = . V1T1 , t=5 T   2          t=-T

^S 4X

^S3X |   = X.V 1 T I ; ^S3X |    = _и ^VT ,

',                              1                 /11           (,                        ,l

S 8X = 7 V T + J A x dt = - V T + J |- 24 V + 87 1 | dt = T V T +| ( - 24 V ) t + 4 -¹ 1 ² I =

⁴        11          ⁴        11- 3            T J ⁴        3              ^T J

_{4                           4} T 1                                                                              4 ^T 1

= 1 VT + ( - 24 V ) t + 4 V ¹ 1 ² + 66 VT -^ VT = 36 VT - 24 Vt + 4 V-1 ².

t

= vV T + J A X d = 4 ₅

₄ T 1

t = T 1     ²             t = 5 T    ⁴

-VT + 4 ^{VT +}

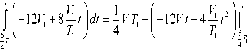
В частности, на концах интервала:

= ¹ VT - 12 Vt + 4 - ^t ² + 15 VT - ²⁵ VT = 9 VT -W + 4 - ‘ ². 11      1                11       11     11      1

S

8X

t = 4 T ¹

¹ VT ; S .X |   = 0 .

⁴            t = 3 t

В частности, на концах интервала:

S4X t=4 T

= ¹ V T ; S 4X |   = о .

⁴           t = 3 T

Далее – повторы (из-за периодичности)

t ^ t + - J

t

S_w = 0 + f A dit =

5X           5 X

3 _T

t i              v.

J |- 3 V + 2 V t

3 T 3         ^T

t

- 3 Vt + Vt ² II

^{T J} 2 j

- 3 Vt + V1 2 + (31)

1     _{T 1}

9      9

+- VT - - VT

11     11

9 _ и ,

- VT - 3 Vt +— t²,

11      1           ^,

В частности, на концах интервала:

S_5X I = 0; S_5X I = ¹ VT ,

5X               5X               1 1

t = ³ T           t = ² T   ⁴

По результатам выполненных расчетов построены графики проекций скорости, ускорения и перемещения горизонтального решета в разные моменты времени, представленные на рисунках 1–3.

По оси абсцисс время отложено в единицах величины Т 1 ≈ 0,21 с. По оси ординат скорость в единицах величины V 1 ≈ 0,28 м/с (рис. 1).

По оси абсцисс время отложено в единицах величины Т 1 ≈ 0,21 с. По оси ординат – ускорение в единицах величины ^{V 1} ≈ 1,33 м/с² (рис. 2).

T 1

По оси абсцисс время отложено в единицах величины Т 1 ≈ 0,21 с. По оси ординат – скорость в единицах величины V 1 = 0,06 м/ Т 1 (рис. 3).

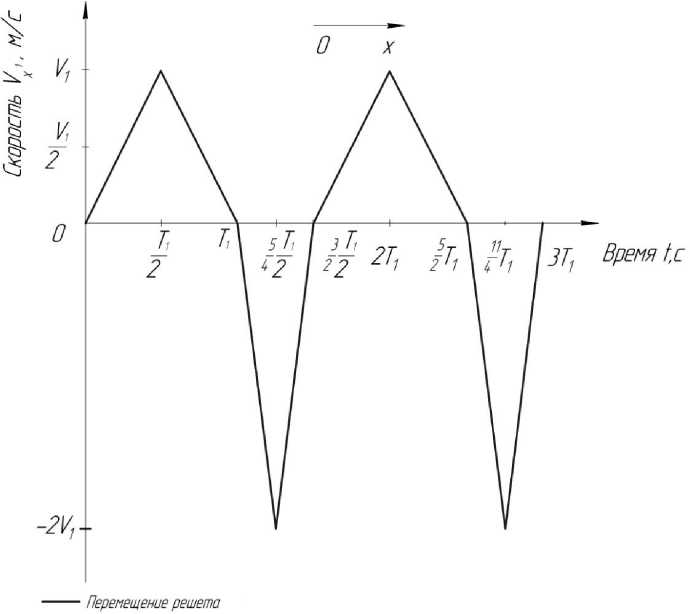
Рис. 1. Проекция скорости решета в разные моменты времени

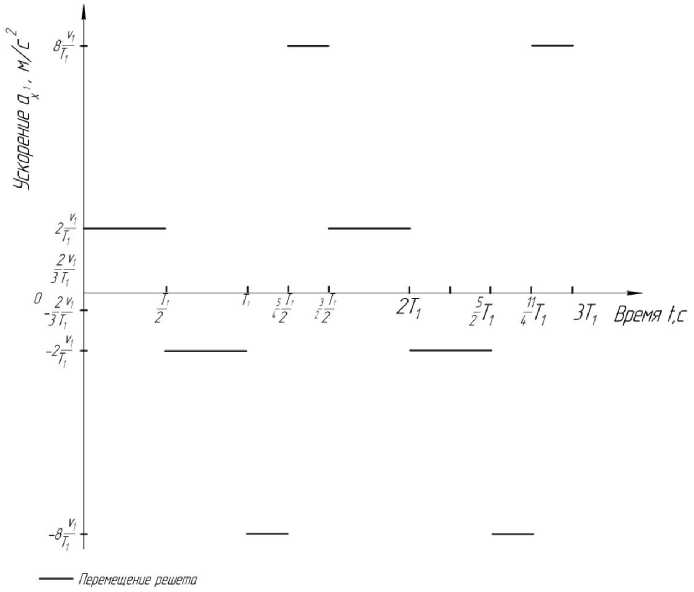
Рис. 2. Проекция ускорения решета в разные моменты времени

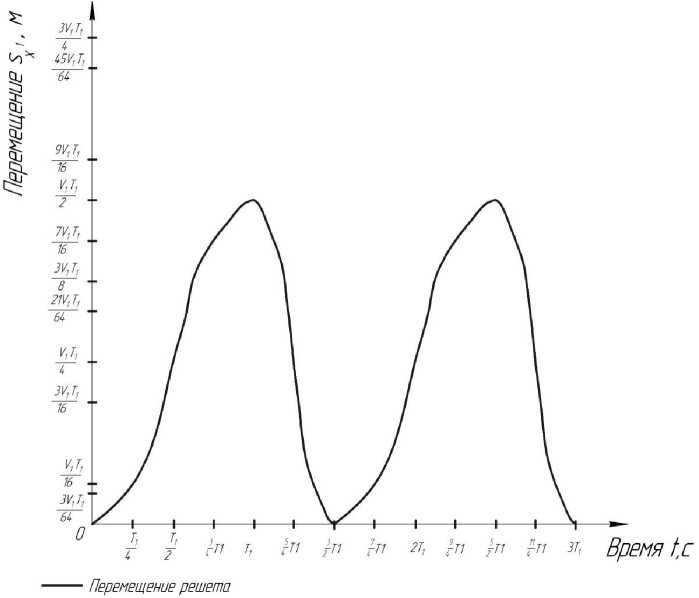
Рис. 3. Проекция перемещения решета в разные моменты времени

Выводы. Данным исследованием определены режимы движения горизонтального решета. На практике это позволит снизить потери семенного материала и повысить качество очистки.

Модель рекомендована для проектирования оборудования по очистке семенного материала сосны сибирской кедровой.