Математическое моделирование движения колесной машины в горизонтальной плоскости

В Алтайском государственном техническом университете им. И.И. Ползунова проводятся исследования, целью которых является разработка и создание системы управления движением колесной сельскохозяйственной машины для отечественной техники, не уступающей по своим характеристикам импортным системам и имеющей более приемлемую стоимость для сельхозпроизводителей [3].

Важной задачей при создании системы управления является разработка алгоритма управления, обеспечивающего движение сельскохозяйственной машины по задаваемой траектории, и его программно-аппаратная реализация. Алгоритм управления условно можно разбить на два больших модуля – глобальное и локальное регулирование [4]. Локальное регулирование обеспечивает реализацию текущего задаваемого значения угла поворота управляемых колес. Реализация задачи локального регулирования описана в [5]. Глобальное регулирование должно по величине отклонения от задаваемой траектории определять величину угла поворота управляемых колес (или угла слома рамы), которую необходимо реализовать, чтобы достичь движения по заданной траектории.

Проверка работоспособности разработанных алгоритмов управления осуществляется экспериментально. Полевые испытания связаны со значительными финансовыми и временными затратами. В последнее время в конструкторско-исследовательской работе широко используется идеология моделирования поведения механических систем в режиме реального времени. Суть ее заключается в том, что большая часть механической системы, за исключением исследуемого узла, описывается механико-математической моделью. При симуляции движения в режиме реального времени исследуемый узел посредством измерительной аппаратуры, блоков ЦАП, АЦП взаимодействует с моделью системы. Таким образом, текущие значения силовых и кинематических параметров исследуемого узла передаются в математическую модель. Соответственно дорогостоящие экспериментальные исследования механической системы можно заменить испытаниями в лабораторных условиях.

Целесообразным представляется проверка работоспособности электромеханической системы управления и разработанных алгоритмов в лаборатории. При проведении эксперимента реально существуют передние управляемые колеса, рулевое управление, подруливающее устройство, представляющее собой электродвигатель с электронным блоком управления, и комплект аппаратуры. Колесная машина заменена ее механико-математической моделью в виде дифференциальных уравнений движения. При интегрировании уравнений в реальном времени система глобального регулирования по отклонениям машины от задаваемой траектории определяет необходимое значение текущего угла поворота управляемых колес, обеспечивающего задаваемое движение. Система локального регулирования реализует приближение текущего угла к задаваемому.

Следовательно, актуальной представляется разработка механико-математической модели колесной машины для симуляции ее движения в режиме реального времени.

Цель исследования : разработка математической модели колесной машины для симуляции ее движения в режиме реального времени, проверка ее адекватности по результатам моделирования стандартных маневров – переставка, движение по кругу.

Для реализации этой цели были поставлены задачи : составить дифференциальные уравнения плоского движения колесной машины; разработать программную реализацию для интегрирования уравнений в среде Matlab [6]; провести математическое моделирование движения и оценить адекватность модели реальному объекту.

Математическая модель колесной машины. При разработке математической модели использовались дифференциальные уравнения плоского движения автомобиля [7]:

n               n              n

M̈c =∑ ^kx ,M̈c =∑ ^ky ,к ̈=∑mc ( ⃗I)․ k=i             k=l            k=l

В модели боковые силы, действующие в контакте колеса с опорой, представляются как функции угла увода. Для определения углов увода через кинематические параметры движения автомобиля (скорость центра масс, угловую скорость в горизонтальной плоскости и его геометрические размеры) рассмотрим схему кинематики плоского движения автомобиля, изображенную на рисунке 1.

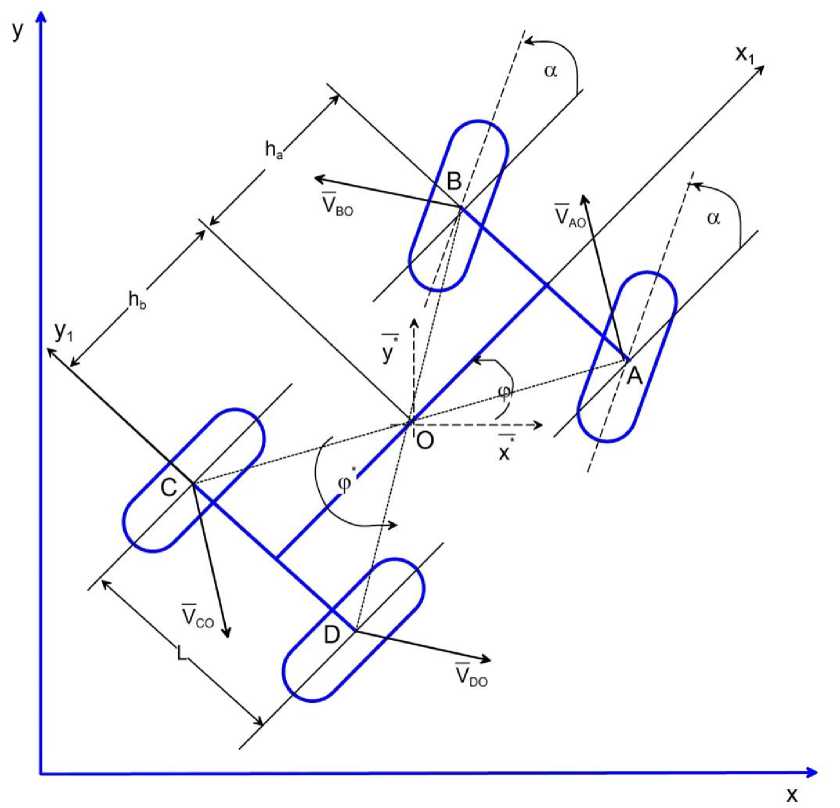
Рис. 1. Кинематика плоского движения автомобиля

На схеме использованы следующие обозначения: Х,У - составляющие скорости центра масс (точка О ); h_a,h _b - расстояние от передней и задней оси до центра масс; а - угол поворота управляемых колес; L - ширина колеи; ф , ф - угол поворота продольной оси в горизонтальной плоскости и угловая скорость; ^⃗ V^⃗ , ^⃗ V^⃗ , ^⃗ V^⃗ , V _D0 - вращательные скорости относительно центра масс.

При составлении кинематических уравнений углы поворота управляемых колес были приняты как одинаковые. Скорости центров колес определяются как векторная сумма скорости центра масс ( ^⃗⃗ ) и их вращательных скоростей относительно центра масс ( V _{A 0} ,V _{B 0} ,V _C0 ,V _D0): —»—»—»   —>—>—>   —>—>—>

V a = V o +V a о ,    V b =V o +V b о ,    V c = V o + V c о ,

^г ^г ^2

^V D = ^V 0 ⁺ V^ D 0 -

Вращательные скорости - это произведение расстояний от центров масс колес до центра масс на угловую скорость автомобиля в горизонтальной плоскости.

После проецирования уравнений на подвижные оси и , связанные с автомобилем, получаем проекции скоростей центров колес на эти оси:

= ̇ сοѕ + ̇ sin + ̇,

=- ̇ sin + ̇ сοѕ + ̇ℎ,

L

= ̇ сοѕ + ̇ sin - ̇,

=- ̇ sin + ̇ сοѕ + ̇ℎ,

L

= ̇ сοѕ + ̇ sin - ̇,

=- ̇ sin + ̇ соѕ - ̇ℎ,

L

= ̇ соѕ + ̇ sin + ̇,

=- ̇ sin + ̇ соѕ - ̇ℎ․

Для задних колес отношение проекции скорости на ось у _г и проекции на ось % ! есть тангенс угла увода (угол, полученный между вектором скорости центра колеса с плоскостью обода). А для передних управляемых колес угол увода вычисляется как разность между углом поворота а и углом, составленным вектором скорости с осью х ^

Соответственно, получаются следующие формулы для определения углов увода:

• -    ̇ о ѕin ф ⁺3^̇ о соѕ ф ⁺ Ч ̇ℎ а

Од =  - arсtan ---------------------- J—

• ̇ Q соѕ ср +з̇ Q ѕin ср + q ̇

• -    ̇ о ѕin Ф ⁺3^̇ о соѕ Ф ⁺ Ч ̇ℎ а Ор =  - arсtan

• ̇ 0 соѕ ф +з̇ 0 ѕin ф - q ̇

• -    ̇ 0 ѕin ф +з̇ 0 соѕ ф - q ̇ℎ ь

^с =-arсtan--------------------- L ,

• ̇ 0 соѕ ф +з̇ 0 ѕin ф - q ̇

• -    ̇ 0 ѕin ф +з̇ 0 соѕ ф - q ̇ℎ ь

^D = -arсtan ----------------------- L ․

Боковые силы принимаются пропорционально углам бокового увода ( Кд , Кд , Кд , Кд – коэффициенты сопротивления уводу колес): Fбок ․ А = ^, Fбок ․ в = , Fбок ․ с = ^, Fбок ․ D = .

Боковые силы ( ^⃗ _бок ) направляются перпендикулярно плоскости обода, движущие силы ( ^⃗ _движ ) и силы сопротивления качению ( ^⃗ _сопр ) – по линии вектора скорости центра колеса в соответствующих направлениях. Силы, действующие на автомобиль, представлены на рисунке 2.

̇ 0 соѕ ф +з̇ 0 ѕin ф + q ̇

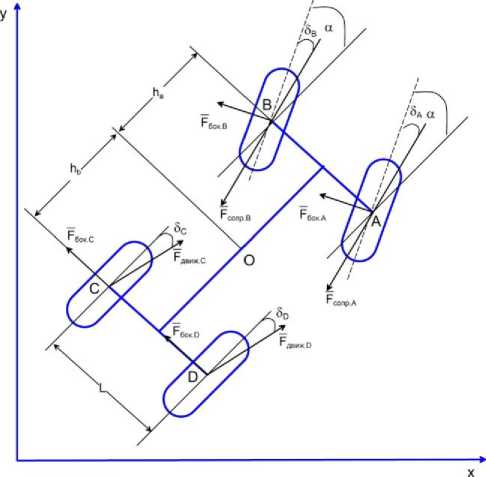
Рис. 2. Силы, действующие на автомобиль

На схеме использованы следующие обозначения: һ_а,һ в – расстояние от передней и задней оси до центра масс (точка О ); α – угол поворота управляемых колес; L – ширина колеи; δ д, δВ , δс , δв – углы увода колес;

⃗⃗⃗⃗     ⃗

F бок ․ А, F бок ․ В, F бок ․ С, F бок ․ D – боковые силы; F _{сопр ․} ^,

⃗⃗

, F сопр ․   –

силы сопротивления; ^⃗F^⃗ _{движ ․} ,^⃗F^⃗ _{движ ․} – движущие силы.

Получаем следующие формулы проекций сил на оси ОХ и 0Y для центров всех колес:

Fax =- Fсопр ․ А соѕ( Ф ⁺ а ^- д_А )- Fбок ․ А ѕin( Ф ⁺ а ), Fbx =- Fсопр ․ в соѕ( Ф ⁺ а ^- дв )- Fбок ․ в ѕin( Ф ⁺ а ), Fcx = движ ․ с соѕ( Ф ^- дс )- Fбок ․ с ѕin Ф ^, Fbx = движ ․ d соѕ( Ф ^- дв )- F бок ․ в ѕin Ф ^, Fay =- Fсопр ․ А ѕin( Ф ⁺ а ^- д_А )+ Fбок ․ А соѕ( Ф ⁺ а ), Fby =- Fсопр ․ в ѕin( Ф ⁺ а ^- дв )+ Fбок ․ в соѕ( Ф ⁺ а ), Fcy = движ ․ с ѕin( Ф ^- дс )- F бок ․ с соѕ Ф ^, Fby = движ ․ в ѕin( Ф ^- дв )- Fбок ․ в соѕ Ф ^․

Моменты сил относительно точки О :

L                                                  L

^МА =- Fсопр ․ А соѕ( а ^- д_А )- Fсопр ․ А ѕin( а ^- д_А )ℎ а ⁺ Fбок ․ А соѕ( а )ℎ а ^- Fбок ․ А ѕin( а ),

L                                                      L

М_в = сопр ․ в соѕ( а ^- дв )- Fсопр ․ в ѕin( а ^- дв )ℎ а ⁺ Fбок ․ в соѕ( а )ℎ а ⁺ Fбок ․ А ^ѕin( а ),

L

Мс =- Fдвиж ․ с соѕ( дс )+ Fдвиж ․ с ѕin( дс )ℎ ь ^- Fбок ․ с ^ℎ ь ^,

L

М_в = движ ․ в соѕ( дв )+ Fдвиж ․ в ѕin( дв )ℎ ь ^- Fбок ․ в ^ℎ ь ^․

Исходя из дифференциальных уравнений движения центра масс и дифференциального уравнения вращательного движения и используя выведенные проекции сил на оси и формулы вычисления моментов сил, получаем сле дующую систему дифференциальных уравнений:

m=o = Fax + FBX + Fcx + Fdx myo = Aay + Fby + Fcy + Fdy,

^оФ = Ma + M_B + M_c + M_D.

Моделирование движения в Matlab. Для того чтобы проверить работоспособность математической модели в пакете Matlab, была разработана функция для вычисления правых частей полученной системы дифференциальных уравнений. Переменные состояния данной функции: координата X; проекция скорости на ось OX; координата Y; проекция скорости на ось OY; угол поворота продольной оси машины; угловая скорость машины в горизонтальной плоскости.

Входные параметры модели: масса автомобиля; расстояние от центра масс до передней оси; расстояние от центра масс до задней оси; ширина колеи; величины сил сопротивления и движения; момент инерции автомобиля относительно центра масс; коэффициенты сопротивления уводу колес.

На рисунке 3 представлены зависимости угла поворота управляемых колес от времени и полученная траектория движения. Угол поворота колес задавался как шаговая функция, которая плавно аппроксимирует переход от одного значения к другому, используя кубический полином.

На рисунке 4 представлены зависимости угла поворота управляемых колес от времени и полученная траектория движения при маневре переставка.

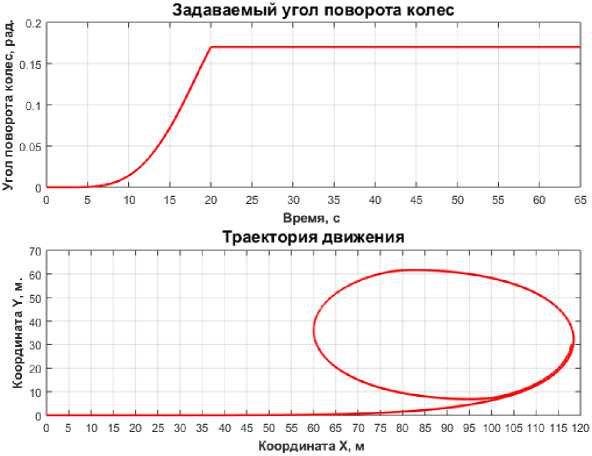
Рис. 3. Результаты моделирование движения по круговой траектории

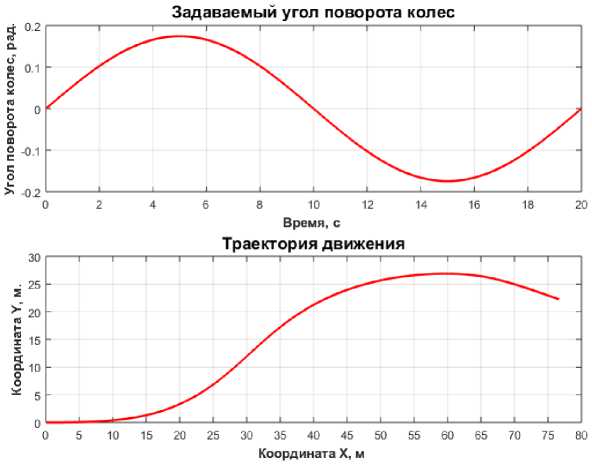
Рис. 4. Результаты моделирования движения при переставке

Выводы. Из анализа рисунков 3-4 можно сделать вывод, что траектория движения при рассмотренных маневрах соответствует действительности.

Следовательно, результаты моделирования в среде Matlab подтвердили адекватность разработанной математической модели реальной машине, что позволяет в дальнейшем использовать ее для симуляции движения колесной машины в режиме реального времени и при разработке алгоритма управления с использованием теории автоматического регулирования.