Математическое моделирование двухкомпонентной среды при акустическом возмущении

Теория акустической эмиссии (АЭ) находит многочисленные приложения в геофизике, сейсмологии, акустике. Метод АЭ успешно применяется для исследования электромеханических эффектов в пористых спеченных композиционных материалах. Относительная простота и наглядность метода АЭ используется при полунатурном моделировании физических процессов в радиотехнике.

В двухкомпонентных пористых средах АЭ возникает в результате быстрых структурных изменений в некоторых областях упругой среды при пластическом сдвиге, изменении атомной структуры, появлении микротрещин и т.п. Такие области в пористой двухкомпонентной принято называть очагами эмиссии.

Гармонические сигналы широко используются при практической реализации метода АЭ. Актуальность гармонического анализа сохраняется при исследовании метаматериалов с электрически управляемой диэлектрической и магнитной проницаемостями, а также композитов обладающих необычными механическими свойствами, например ауксетиков, имеющих отрицательные значения коэффициента Пуассона.

Построению математической модели двухкомпонентной среды при гармоническом акустическом возмущении посвящена данная работа.

1 Математическая модель АЭ в двухкомпонентной среде

Наличие очага эмиссии (ОЭ) в пористом коллекторе порождает сме-

ТТ (1)                                                           rr(!)e щения элементов среды Ui , которые можно разделить на упругие Ui и спонтанные Ui(1)s [1, 2, 3, 4, 5]

Up) = Up + Up

.

Основной характеристикой структурного превращения среды в ОЭ являются спонтанные перемещения p^l)s или тензор спонтанной дисторсии, записанный в виде Up = U i^s , где запятая внизу означает дифференцирование по j –координате.

По повторяющимся одинаковым индексам здесь и в дальнейшем проводится суммирование от одного до трех.

Из (1) находим упругие смещения U i^e = U i ¹ — U i ⁽¹⁾ s . Дифференцируя это выражение, приходим к тензору упругой дисторсии

^(1)e — f/^(l)e — ¹ (I /⁽¹⁾ I /7⁽¹Л T/^(1)s u ij  = ^U i,j = ₂ рЗ ⁺ U j,i / - U i,j .

(l) e

Для двухкомпонентной среды тензор упругой дисторсии u _ij связан с тензором напряжений T ij и силой N , действующей на вещество, заполняющее поры, обобщенным законом Гука [3 , 4]

Tij = X*uWe5ij + 2^*и^е + (J-L^vj, N = Q*u$ + R*UA, где N — сила, отнесенная к единице площади поперечного сечения пористой среды; λ∗ , µ∗ — комплексные коэффициенты Ламе; индекс 1 вверху в круглых скобках относится к упругой компоненте, 2 — к веществу, заполняющему поры; δij — символ Кронекера. Комплексные коэффициенты Q*, R* зависят от пористости среды m (0 6 m 6 1) и сжимаемости межпористого вещества R*. Они определяются зависимостями

Q * = (1 - m)R * ,  R * = mR * .                  (4)

Выразим тензор T ij среды через смещения элементов пористой среды и спонтанные упругие перемещения. Для этого подставим (2) в (3) , получим

T ij = X * U^ + Ц* ( j + U j, !)) + Q * Ugd ij N = Q * U$ + RU ^r .

-

2^ (T, i,j            ₍₅₎

По повторяющимся индексам латинских обозначений проводится суммирование от единицы до трех, греческих – от единицы до двух.

Дифференцируем (5) по j –координате, получим

T jj = (X * + ^u j + ^u j - 2p * u j + Q * u j , N ,j = Q * u j + R * u j

Запишем уравнения движения двухкомпонентной среды с учетом вязкости вещества, заполняющего поры [6 , 7 , 8 , 9]

d ²^¹

^P "dt2- ^{+ P 12}

d ² U i ⁽²⁾ dt ²

+ b^ (U ^{( (1)}

∂t ⁱ

-

U _i (2)

= T- ■

Tij,j,

d ² U i ⁽¹⁾        d ² U (2)

^{p 12} ^t^ ^{+ P 22} ^i^ —

ьд ^u?

— U ⁽²⁾) = N ,j ,

где P 11 , P 22 — эффективные плотности твердой компоненты и межпористого вещества; Р 12 — динамический коэффициент связи компонентов пористой структуры. Постоянная b — величина, обратно пропорциональная подвижности межпористого вещества и определяемая по формуле b = ⁿ? m-, где п и к — коэффициенты вязкости и проницаемости пористого коллектора, соответственно.

В. С. Поленов, Л. А. Кукарских, Д. А. Ницак. Математическое моделиро- вание двухкомпонентной среды ...

С учетом (6) уравнения движения (7) принимают вид д 2Ui(1)

P11 "^t^"

d ² U i ⁽²⁾

^{+ P 12}

+bs ■   - U?’ ⁾ =

= (A* + д*) Uj + **uj - 2. * U + Q*uj д2 Ui(1)        д2 Ui(2)

bd (U *¹’ - U i ² ) =

^{P 12} ^t^ ^{+ P 22} ^t^ —

= Q * u j + R - U j .

После описываемая Био тематика была развита в многочисленных публикациях, в том числе и в монографиях [10 , 11 , 12] , в которых, в частности, содержатся ссылки на библиографические обзоры, посвященные обсуждаемой проблеме.

Запишем систему (8) в безразмерной форме. Для этого уравнения (8) разделим на ρH , где

P = P 11 + 2p 12 + P 22 ,

H = A1 + 2^1 + R1 + 2Q1, где A1, ^1, R1, Q1 — действительные части комплексных чисел λ∗, µ∗, R∗, Q∗.

С учетом условий (9) , систему (8) преобразуем к виду

H

д 2 U _i (1)        д 2 U _i (2)     b д ₍₁₎

Y 11— ⁺ Y 12— "КЗ 1о? ( U dt ²            dt ²      р dt \ i

-

_{U i} (2)

= P [(^ 111 + ^ *12 )U j + ^ 1*12 U ⁽ j ₃ - 2^ 12 ^ 5; + ^ *2 Ug i ] ,

H

d ² U i ⁽¹⁾

dt ²

+ Y 22

д ² U i ⁽²⁾

dt ²

-

b ® ⁽u °) ρ ∂t ^{U i}

-

U _i (2)

= P       ■'      + ^ff 22 U jj ’ ] .

где приняты обозначения

Y ij = ^p pj ,    (i,j = 1, 2),

∗ ^{λ ∗} ^и = H,

^ ¹¹² = H,

^ 11 = ^ 111 ^{+ 2a} .,2 =

A ¹ + 2^ *

H

(1 - m)R5    z. . *     *   R*     *        *

= --- у --- = ^{(1 - m)}^ , O = —,   0 22 = m° •

HH

Параметры пористой среды должны удовлетворять условию нормировки

Х 11 + 2X 12 + X 22 = Y 11 + 2Y 12 + Y 22 = 1,              (12)

где x ij — действительная часть комплексного числа σ _i ^∗ _j Умножим оба уравнения (10) на H, получим

d ² u ⁽¹⁾        d ² u ⁽²⁾     ь d /_rr(1)

Y 11 ⁺ Y 12 1 U^i dt ²            dt ²       p dt \ ⁽

-

U ⁽²⁾) =

H

ρ

[(^ *11 ⁺ ^ 112 ) U jj ^{+ CT} *12Ui, jj ^{- 2CT} *12 U ((1j3 ⁺ ^ 12 ^U j,j/ J ,

d ² U ₍ ⁽¹⁾        d ² U ²

Y12  .-■+ Y22 -де-

b∂ ρ ∂t

U ₍ (1)

-

_{U (} (2)   ₌

=H ■■     + ■■    ].

Решение системы (13) будем искать в виде акустических волн [13]

U ₍ ^{( n ) p} = C ₍ ^{( n )} exp I (© p X ( V ( - wt) , U ₍ ^{( n )} s = C ₍ ^{( n )} exp i (© S х^г - wt), n = 1, 2, i = V- 1,

где C ₍ ⁽ⁿ⁾ — амплитуда колебаний; w = 2nf — круговая частота (f — циклическая частота); v — координаты единичного вектора в направлении распространения акустической волны в среде; © p , ©S — комплексные коэффициенты, учитывающие затухание и фазовую составляющую при распространении акустических волн в пористом коллекторе.

Подставим (14) в (13) , после несложных преобразований получим

- f [(^ 111 + ^ 112 ) © p ² C (¹⁾ VV j + ^ 112 © p ² C ⁽¹⁾ +

+^1*2SpC^ViVj - 2^112 qsp ©S2C(1)] + bw (1)                bw (2)

+ Y1 1 W ² + I—  C- + Y 12 W ² - i— C¹ - 0,

^{ρ                      ρ}                     (15)

- HP ! - i.pV2 v v + -;2©p2C 2 v v ) + bw (1)                bw (2)

+ Y12W2 - i— C J + Y22W2 + i— C — 0, ρ                   ρ где qsp = exp [-i (©p - ©S) XiV(].

2 Характеристики акустических волн в двухкомпонентной среде

Характеристики акустических волн определим из системы (15) , если умножим оба уравнения (15) на v i и просуммируем по повторяющемуся индексу i с учетом V i V i = 1. Полагаем C i ^{( n )} V i = D n = 0 и совмещаем ОЭ с началом координат X i = 0. В результате получим систему

[(7 11 + IY) w ² - И1 © Р 2 — 2^ *12 0 :2 ) V 2 ] D 1 +

⁺ [⁽7 11 ^{— l}Y) ^w 2 ^{— y} 12 © p² V 2 ] D 2 = ⁰,

[(711 — 17) w2 — CT12©P2V2] D1 + + [(y22 + 17) w2 — ^2©Р^2] D2 = 0, где V = ^Н/р — скорость распространения акустических волн; 7 = ρbω — параметр, характеризующий диапазон частот акустических волн. Условие y ^ 1 соответствует случаю низких частот [9].

Для того, чтобы однородная система (16) имела нетривиальное решение, необходимо, чтобы ее определитель, составленный из коэффициентов при неизвестных D _n , был равен нулю [14]

a 11 a 12

a 21 a 22

где ail = (th + 17) w2 — (on©p2 — 2^112©S2) V2, a12 = a11 = (Y12 — I7) w2 — y12Qp2V2, all = (y22 + 17) w2 — ^22©p2V2.

После раскрытия определителя, получим

H © p ⁴ — 2 _CT *112 _CT *22 © p ² © *s 2 ) V 4 +

⁺ [^{( — y} 11 ^ 22 ⁺ 2^Y 12 ^ 12 ^{— Y} 22 ^ 11 ) © P 2 ⁺ 2^Y 22 ^ 112 © S 2 ] ^w 2 V 2 ^{+ Y} X ^w 4 ^{— (}1⁷⁾

—IY [(^s©p2 — 2^112©:2) w2V2 — w4] = 0, где ^s = ^11 + 2^12 + ^22, ^X = ^11^22 — ^12, YX = Y11Y22 — 712•

Преобразуем выражение (17) к системе двух уравнений относительно

^ X © P 2 V ^{2 — ( y} 11 ^ 22 ^{— 2 y} 12 ^ 12 ^{+ y} 22 ^ 11 ) ^w 2 ^—

• — I7^ S W 2 = 0,

• ^{— 2}^ 111 © S 2 ^V 2 (^CT 21 © p ^{2 V} 2 ^{— 7} 11 ^w 2 ) ^{+ 7} X ^w 4 ⁺

+I7 (2^ 112 © : ² w ² V ² + w ⁴ ) = 0.

Обозначим 0 р = в _Р + ia _p , где в р , a p — фазовая постоянная распространения и коэффициент затухания акустической волны в пористой среде и 0 * = e s + ia s , где e s , a s — фазовая постоянная распространения и коэффициент затухания волны спонтанных перемещений.

Из первого уравнения (18) получаем

α _p

^€ g ^{+ €} y - ^€ х = V \  2 (c g + c 2 ) '

ω

. =

У^€2 ⁺ € У ^{+ €} » V \  2 (c g + c 2 )  '

ω

где

^€ g -   (cry S    c y ) ^{Y +} aXc g ⁺ a y c y '   ^€ y - (cg ⁺ c y y s ) ^Y    axc y ⁺ a y ^cX '

a x = Y 11 X 22 - 2Y 12 X 12 + Y 22 X 11 ,   a y = 7 1№ - 2Y 12 y i2 + Y 22 У 11 ,

Cx = X11X22 — X12 — У11У22 + У22,  cy = Х11У22 - 2Х12У12 + Х22У11, ys = У11 + 2У12 + У22

и определяем скорость распространения акустической волны в пористой среде

ω

^{C p} =в р = V

² (c x ⁺ c

\| / g + € 2 + € x .

Используем для подстановки во второе уравнение (18) 0р2 = Ap + iBp, где

ω ²    ξ x             ω ²    ξ y

^Lp    V ² c g + c y ' p V ² c g + c y '

определим коэффициент затухания и фазовую постоянную распространения волны спонтанных перемещений

Ш (dg + dy) (y 2 + y! ) - dgYA - dy Y as = V N            2 (dg + dy)

ш     (dg+ dy) (Y2 + Ya) + dxY! + dy Y e‘ = VN            2 (d2 + dy)

где dg = —2x112 (Y22 — x22Ap + y22Bp) + 2y112 (Y — x22Bp — y22Ap) '

^d y = ^— 2x 112 ⁽Y ^{— x} 22 B p ^{— у} 22 ^А р ) ^{— 2y} 112 ⁽Y 22 ^{— x} 22 A p ^{+ у} 22 ^В р ) •

Из выражения c s = вр получим формулу для определения скорости распространения волны спонтанной дисторсии в ОЭ

C s = V

2 И + dy)

\   (^d X ⁺ d y ) ( y ^{2 +} Y a ) ^{+ d} x Y A ⁺ d y Y

Скорость акустических волн в пористом коллекторе можно найти как сумму c = Cp + Cs.                               (24)

Таким образом, зная комплексные коэффициенты пористого коллектора, по формулам (19) , (20) , (21) , (22) , (23) и (24) можно определить характеристики акустических волн в пористом коллекторе и в ОЭ коллектора.

3 Примеры

При выполнении расчетов полагаем: р = H/V ² = 10; b = m ² при допущении к = п- Решаем (v — 1) qx = (2v ² + v — 1) (2 — m) относительно ν , находим коэффициент Пуассона

V 1 , 2 =

2 — qx — m T ^ qx [qx + 10 (m — 2)] + 9 (m — 2) 2

4 (m — 2)

где q = E/Re[R 0 ] > 1 (E — модуль Юнга), x = —p + x ²² - Коэффициент Пуассона необходим для связи ст *12 = 2 V— 2 ^ *1 -

Исходные данные для расчетов, определенные с учетом (4) , (11) , (12) и (25) , сведены в таблицу 1 .

Таблица 1: Исходные данные для расчета (v > 0)

m	ν	x 11	y 11	x 112	y 112	x 12	y 12	x 22	y 22
0.2	0.363	0.64	0.16	0.14	0.007	0.16	0.009	0.04	0.002
0.5	0.33	0.65	0.162	0.17	0.008	0.12	0.006	0.12	0.006
0.8	0.246	0.68	0.166	0.19	0.012	0.05	0.004	0.22	0.015
Y 11 = 0.7; Y 12 = — 0.01; Y 22 = 0.32

Изменение знака перед коэффициентом Пуассона соответствует наделению материала свойством ауксетика. Этим свойством обладают многие металлы, анизотропные кристаллы, полимеры. При этом пересчету подлежит только σ ₁ ^∗ ₁₂ . Ее действительная и мнимая части представлены в таблице 2 как дополнительные исходные данные.

Таблица 2: Дополнительные исходные данные (ν < 0)

m	ν	x 112	У 112
0.2	- 0.363	0.4052	0.1058
0.5	- 0.33	0.4049	0.1073
0.8	- 0.246	0.4169	0.1092

На рисунке 1 как функции от y представлены зависимости c(Y-Y0), где Yo = -0.05. Смещением функций вдоль оси абсцисс реализован режим «логарифимического микроскопа» в области малых отрицательных значений γ. Сплошной линией показаны зависмости при ν > 0, пунктирной – при ν < 0. Для повышения наглядности нормированные функции скорости отображаются в логарифмическом масштабе.

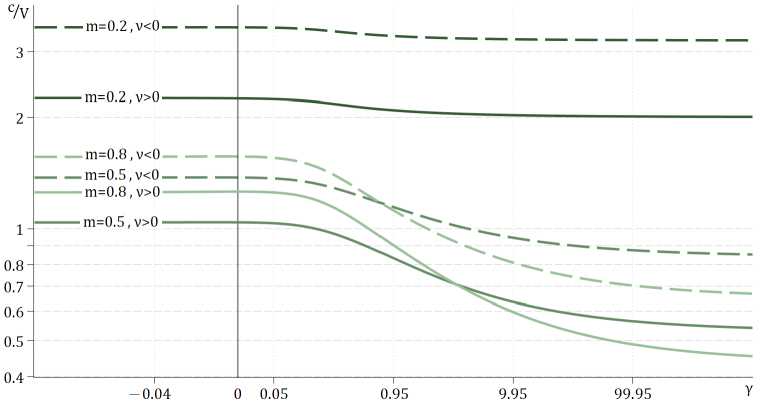
Рис. 1: Скорости распространения волн в пористом коллекторе

Как видно из графиков рисунка 1 , функции скорости монотонны и проявляют характер фильтра высоких частот. Для ν < 0 нормированная скорость спонтанной дисторсии больше, чем для ν > 0, следовательно, выше и нормированные скорости распространения волн в пористом коллекторе. При пористости m = 0.2 скорости спонтанных дисторсий проявляют слабую зависимость от частоты.

Заключение

• 1.    Комплексные коэффициенты пористого коллектора позволяют определить характеристики акустических волн в самом коллекторе и в очаге эмиссии коллектора.

• 2.    Пористый коллектор обладает дифференцирующими свойствами по отношению к скорости распространения внутренних волн.

• 3.    Скорость спонтанной дисторсии в ауксетиках при прочих равных условиях выше, чем в материалах с положительным значением коэффициента Пуассона.