Математическое моделирование фазочувствительного режима работы схемы радиоимпульсного стробирования

DOI:

Вопросы исследования формы огибающей и фазовой структуры периодической последовательности когерентных радиоимпульсов возникают в задачах импульсной рефлектометрии и радиолокации при полунатурном моделировании [1]. Для этой цели используются стробоскопические методы трансформации временного масштаба, позволяющие согласовать частотный диапазон широкополосных радиосигналов с возможностями измерительной аппаратуры [6; 9]. Сочетание стробоскопической трансформации с обработкой информации на ЭВМ значительно расширяет области применения этих методов [7; 8].

В настоящей работе рассматривается модель радиоимпульсного стробоскопического преобразователя, работающего в специальном режиме преобразования фазовой модуляции в амплитудную. Такой режим позволяет производить измерения внутриимпульсной фазовой модуляции радиосигналов наносекундной длительности без применения дополнительных фазочувствительных элементов.

При анализе используется математическая модель стробоскопического преобразователя [6; 11], состоящая из перемножителя (смесителя) и узкополосного фильтра, настроенного на разностную частоту несущих (рис. 1):

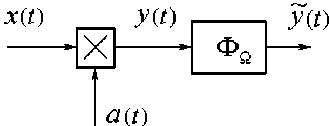
Рис. 1. Математическая модель стробоскопического преобразователя

Модели сигналов x ( t ) и a ( t ) представляются в виде когерентных узкополосных процессов на интервале наблюдения t е (0, NT ):

N

x ( t ) = ^ A ( t - kT )cos [ ® ₀ t + 0 ( t - kT ) ] ;

k = 0

N

a ( t ) = ^ A 1 ( t - kT 1 )cos [ ® 1 1 + ф(t - kT 1 ) ] .

k = 0

Здесь A ( t ), A 1 ( t ) - огибающие; ©₀, © 1 - несущие частоты; 0( t ), ф( t ) - внутриимпульсная фазовая модуляция входного x ( t ) и стробирующего а ( t ) радиосигналов соответственно; © ₀ - © 1 = Q - низкая промежуточная частота (Q<<© ₀, © 1 ); T - период повторения входного сигнала; T 1 = T + А T ; A T = T/N - шаг считывания; N - коэффициент спектральной трансформации ( N >> 1).

Используя асимптотический подход, развитый в работах [2; 4], и полагая достаточно малой длительность стробирующих радиоимпульсов, сигнал на выходе перемножителя (рис. 1) асимптотически (при N ^ да ) приводится к виду:

~

У ⁽ t ) =

⁽ю n + ^{Q )} t + 9| — | — ф₀ I N )

+ cos

(©„-Q) t -el - n        IN

+ Ф 0

где A 1 - площадь огибающей стробирующего радиоимпульса; ф ₀ - его «средняя» фаза [5]; © n = 2 п n]T 1 - частота n -й гармоники частоты повторения стробирующих импульсов ( n = 1,2, 3 . „). Вид амплитудного спектра в низкочастотной области на выходе перемножителя для Q < л/ T 1 представлен на рисунке 2.

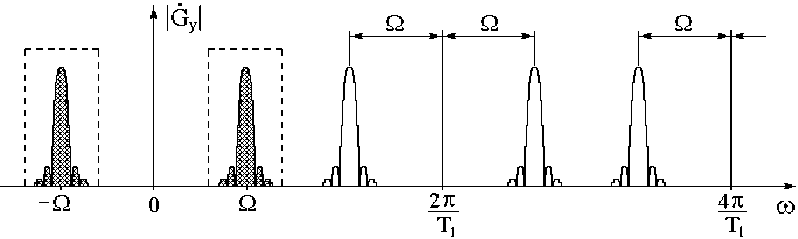
Рис. 2. Вид спектра в низкочастотной области на выходе перемножителя при Q < л/ T 1

При выделении спектральной компоненты на разностной частоте несущих узкополосным фильтром Ф ^ , на выходе преобразователя будет сформирован сигнал на частоте Q с трансформированной во времени огибающей A ( t/N ) и внутриимпульсной фазовой модуляцией 0 ( t/N ) :

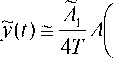
cos

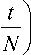
q t +0 —

V N

- ^ф 0

В фазочувствительном режиме из суммы в (2) путем фильтрации выбираются две спектральные компоненты с близкими частотами to n + Q и to n _{+ 1} — Q (рис. 3):

~ ( t ) = A^L A

4 T (

t )

N J

cos

^{( to} n ^{+ Q )} t ⁺ ®| I - ^ф 0 V N J

+ cos

^{( to} n + 1

— Q) t — of — | + ф₀ V N J

сумма которых преобразуется к виду:

A (

~ ( t ) = -1- A 2 T

t

N

cos

Q—F t + 0fF1 —Ф о

V T 1 J V ^{N J} 0

^{X cos( to} n + 12 t ) ,

где ^to n + 12 = ^{2 n ( n +} V²⁾/ T 1 .

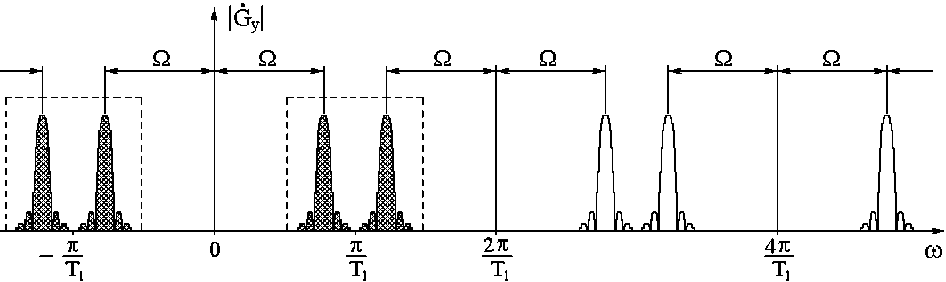
Рис. 3. Фильтрация спектральных компонент для Q < п/ T 1 ( n = 0)

Преобразование фазовой структуры исследуемого сигнала x ( t ) в изменение амплитуды y ( t ) происходит при синхронизации разностной частоты несущих Q с периодом повторения радиостроба a ( t ):

2п[     1)

где p = 0,1,2...

Q = —I p + I,

,

T1 V     Jv

На рисунке 4 показан амплитудный спектр сигнала y ( t ) при выполнении условия (4) для p = 0.

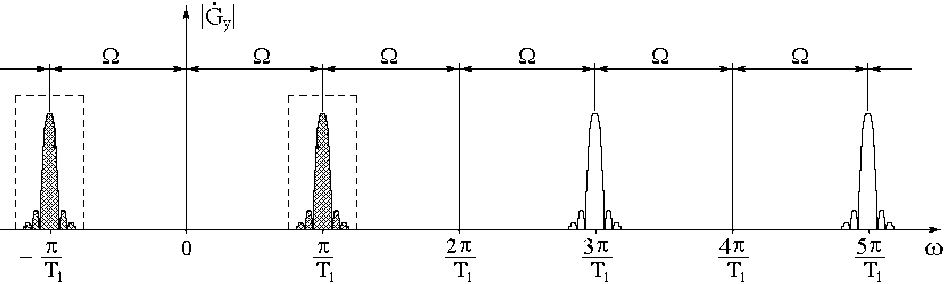
Рис. 4. Амплитудный спектр на выходе перемножителя в фазочувствительном режиме работы стробоскопического преобразователя ( p = 0, n = 0)

При этом сигнал на выходе преобразователя имеет вид:

~ ( t ) = A A I

2 T (

t

N

cos

el— |—ф₀ ( N J

x cos(Q t )

Таким образом, сдвиг несущей частоты стробирующего радиоимпульса на величину, кратную нечетному числу первой субгармоники частоты стробирования, позволяет преобразовать фазовую структуру радиосигнала 9( t ) в модуляцию огибающей без применения дополнительных фазочувствительных элементов. При этом измерение фазовой структуры может производиться на низкой промежуточной частоте Ω амплитудными методами.

Для моделирования работы радиоимпульсного стробоскопического преобразователя использовался экспериментальный макет [3], функциональная схема которого приведена на рисунке 5.

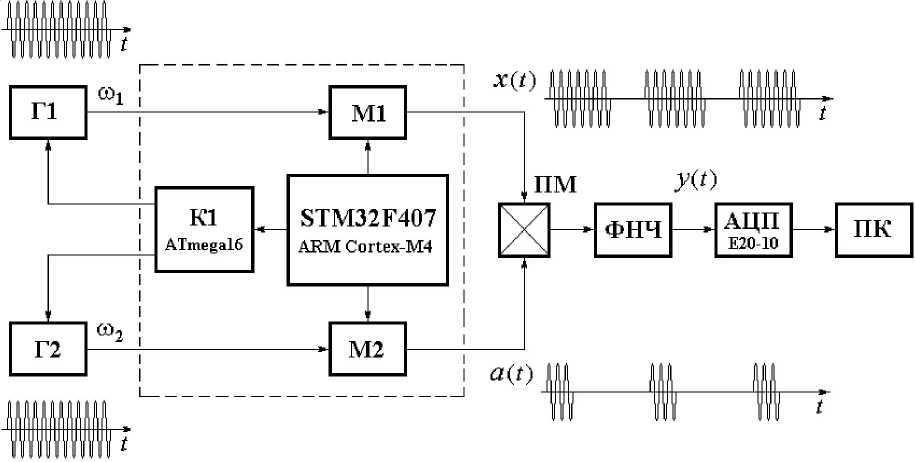
Рис. 5. Макет радиоимпульсного стробоскопического преобразователя

Цифровая часть макета (на рис. 5 выделена штриховой линией) включает в себя микроконтроллер K1 (ATmega16), микропроцессор STM32F407 и два мультиплексора М1, М2 (OPA3875). Аналоговая часть состоит из двух цифровых генераторов Г1 и Г2 (AD9851), перемножителя ПМ (MPY634) и фильтра нижних частот (ФНЧ).

Микроконтроллер К1 служит для настройки генераторов Г1, Г2 на заданную частоту. Генераторы вырабатывают непрерывный гармонический сигнал с частотами F ₀₁ = 10,010 МГц и F ₀₂ = 10,0 МГц. Сигналы подаются на мультиплексоры, на выходе которых получаются исследуемый x ( t ) и стробирующий a ( t ) радиоимпульсы прямоугольной формы с длительностями τ _x = 30 мкс и τ _a = 0,5 мкс соответственно. Далее сигналы x ( t ) и a ( t ) поступают на коррелятор разностной частоты, состоящий из перемножителя (ПМ) и фильтра нижних частот (ФНЧ) с частотой среза ~20 кГц. Сигнал разностной частоты, выделяемый ФНЧ, подвергается дискретизации аналогово-цифровым преобразователем (АЦП) Е20-10.

Поскольку преобразованный сигнал получается на разностной частоте F _Ω = 10 кГц, в персональном компьютере (ПК) реализован цифровой узкополосный КИХ-фильтр порядка 10⁴ с шириной полосы пропускания ~50 Гц. Расчет коэффициентов импульсной характеристики фильтра производился по методу взвешивания; в качестве весовой функции использовалось окно Блэкмана [10], спектральные характеристики которого позволяют достичь неравномерности в полосе пропускаяния ~0,002 дБ и затухания в полосе подавления ~57 дБ. Коэффициент спектральной трансформации огибающей в макете составляет N = 5 000.

На рисунке 6, а представлен выходной сигнал схемы радиоимпульсного стробирования при работе преобразователя в обычном режиме (спектральная диаграмма показана на рис. 2), когда субгармоники частоты повторения лежат за пределами полосы пропускания узкополосного цифрового фильтра системы.

Фазочувствительный режим схемы радиоимпульсного стробирования экспериментально проверен на работоспособность. При практической реализации этого режима в схеме макета тактовая частота системы F T = 1 T получалась путем удвоения разностной частоты несущей F_Q = Q/ 2п , поскольку она остается неизменной при изменении коэффициента спектральной трансформации N . Неизменность тактовой частоты является необходимым условием синхронизации работы высокочастотной и низкочастотной части макета. Однако при этом из соотношения (3) следует, что в огибающей преобразованного сигнала ~ y ( t ) появляется дополнительная линейная фазовая модуляция А9( t ) = AQ t , где

AQ = nf- - — 1

I T T J

n

NT ^.

Эта величина будет восприниматься стробоскопической системой обработки как доплеровский сдвиг несущей частоты. Оценка дополнительного набега фазы Аф за время длительности выходного сигнала ~ u = N т _u дает величину

п

Аф = AQt, ^ u Q, которая не зависит от коэффициента спектральной трансформации (не уменьшается с ростом N) и определяется только скважностью сигнала Q = T/тu.

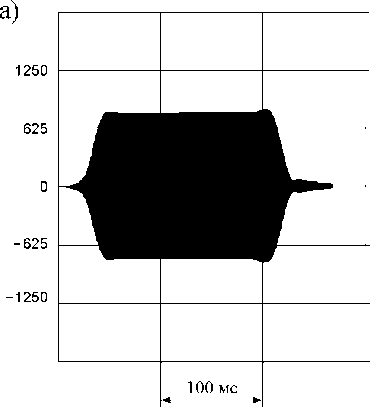
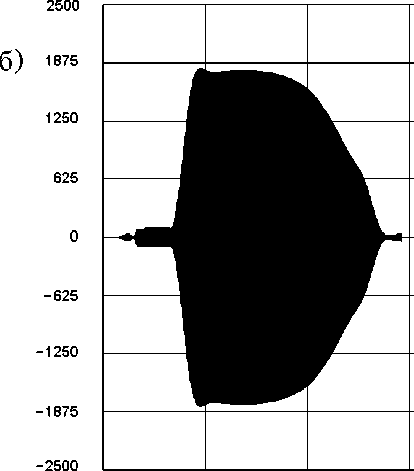
Рис. 6. Сигнал на выходе макета радиоимпульсного стробоскопического преобразователя при F _т > 2 F _Ω ( а ) и в фазочувствительном режиме ( б ) при F _т = 2 F _Ω (масштаб указан в отсчетах АЦП)

На рисунке 6, б приведен результат полунатурного моделирования фазочувствительного режима при F T = n/Q , 9( t ) = 0 , ф₀ = 0 . Длительность входного сигнала составляет т _u = 30 мкс; частота повторения F_T = 20 кГц. В соответствии с соотношениями (6) и (7), расчетный дополнительный набег фазы за время длительности импульса составляет ~0,6 п и искажает прямоугольную огибающую добавлением множителя ~ cos( AQ t ), что хорошо видно на рисунке 6, б .

ПРИМЕЧАНИЕ

• ¹    Работа подготовлена по материалам исследования, выполненного при финансовой поддержке Российского фонда фундаментальных исследований и Администрации Волгоградской области в рамках научного проекта № 15-47-02438-р_поволжье_а.