Математическое моделирование газофазной конденсации металлических наночастиц в камере с дуговым разрядом

Газофазный синтез является одним из методов получения металлических наночастиц и заключается в переводе расплавленного металла в газовую фазу с последующей конденсацией паров в атмосфере холодного инертного газа. Известны несколько вариантов этого метода: плазмохимический синтез, электровзрыв, лазерная абляция и т.д. [1–6]. Почти во всех экспериментальных реализациях метода образованные кластеры подхватываются конвективными течениями и распространяются по всему объему рабочей камеры, постепенно осаждаясь на ее стенках.

Математическое моделирование газофазного синтеза выполняется с целью подбора параметров процесса – формы рабочей камеры, давления и температуры в ней, расположения источников тепла, вида инертного газа и др. – для получения наночастиц с наперед заданными характеристиками.

В процессе кластерообразования в камере образуется неравновесная многофазная среда, в которой наряду с атомами инертного газа и металла содержатся также твердые и жидкие металлические частицы. Сложность количественного описания такой среды заключается в необходимости решения задач на разном уровне размеров и времен, т.к. описание формирования наноструктур включает две составляющие: макроскопическую часть (конвекция, диффузия, перенос тепла в объеме рабочей камеры и т.д.) и микроскопическую или атомную часть (формирование критического зародыша, рост нанокластеров, выделение скрытой теплоты конденсации). Способы раздельного описания макроскопических и микроскопических процессов хорошо известны. Описание макроскопических процессов происходит в рамках уравнений непрерывной среды, которые хорошо изучены и уже используются на уровне инженерных пакетов. Для изучения микроскопических процессов также созданы разнообразные пакеты молекулярной динамики: LAMMPS, SIESTA, CPMD и другие [7–10].

Количественное взаимодействие между микро- и макропроцессами не установлено на достаточном уровне, так, чтобы использовать данные микроскопического моделирования при описании выхода готового продукта. Поэтому на данном этапе предлагается использовать термодинамические теории гомогенной нуклеации [11, 12], хотя известно, что количественное расхождение между термодинамическими расчетами скорости нуклеации и результатами экспериментов может составлять несколько порядков [13, 14]. Мы ожидаем, что термодинамическое описание позволит выявить, по крайней мере, качественные закономерности кластерообразования.

Схема численного эксперимента

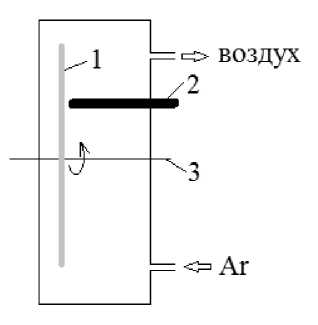
В методах газофазной конденсации подвод энергии для испарения может осуществляться дуговым разрядом. На рис. 1 показана схема такой установки. Дуга формируется между электродом-стержнем и электродом-диском и вызывает испарение материала стержня. Электрод-диск изготовлен из тугоплавкого материала и может вращаться вокруг своей оси. Из камеры откачивают воздух и наполняют аргоном, так что распыление материала стержня происходит в разреженный инертный газ, а вращение диска придает разлету интенсивный характер.

А

Рис. 1. Вид камеры с дуговым разрядом: а) вид сбоку; б) вид спереди; 1 – электрод-диск, 2 – электрод-стержень, 3 – ось вращения электрода-диска

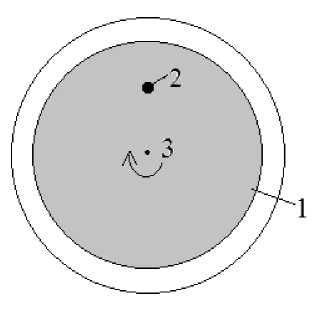
б

Математическая модель представляет собой систему уравнений для макроскопических величин: скорости, температуры, плотности смеси и массовых долей атомов и кластеров металла в каждой точке камеры реактора

^P V + y( p V ® V) = -V P + V П V V + V V ^T )) + p g , (1) d t

Ip + V( p V ) = 0, d t dpCT, p— + V( p V T ) = V(kV T) + Q,(3)

о t

^A^ + V( pV CAr ) = V( pD V CAr), d t

^ + V( pV CM1) = V( pD V CM1) + pR M1,(5)

dpCML + V( pVCMn ) = -V( pDV CMn ) + pRMn , n = 2, Nmax.(6)

В системе (1)–(6) уравнения (1) и (2) представляют собой законы сохранения импульса и вещества, (3) – уравнение теплопроводности, а (4)–(6) описывают конвективную диффузию атомов аргона Ar, металла M₁ и металлических кластеров M _n , содержащих n атомов. В уравнении (6) N _max ~ 10¹¹ равно числу атомов в самом большом кластере, который может быть учтен [15]. Приняты следующие обозначения: V = { V r , V g , V ,} - скорость газодинамических течений в камере, Т – температура газовой смеси, ρ – плотность, C _Ar , C _М – массовая доля аргона и кластеров металла в смеси. Кластеры полагаются малыми, так что можно считать, что они увлекаются потоками газа. В качестве уравнения состояния газовой смеси использовалось уравнение идеального газа.

Физика

Разбиение задачи на взаимодействующие между собой составляющие: газодинамическую и микроскопическую, связанную с нуклеацией, проявляется в том, что в правых частях уравнений (3), (5) и (6) содержатся слагаемые, описывающие выделение скрытой теплоты конденсации и слагаемые-источники для атомов и кластеров металла. Эти величины появляются из-за того, что состав газовой смеси и ее температура изменяются не только в результате диффузионных и конвективных процессов, но также из-за процессов объединения атомов металла в кластеры и обратных процессов их распада. Электрическая часть дуги в работе не описывается, вместо этого задается температура в месте расположения электрического контакта и расход материала стержня в секунду. Оба эти значения выбираются в диапазонах, наблюдающихся в эксперименте.

Систему (1)–(6) дополняют граничные условия. Границы камеры считаются изотермическими, на них выполнены условия прилипания и непроницаемости, т.е.

U = 0, V = 0, W = 0, T = 300 K , C = 0, n = I, N     d C l. /d n = 0.         (7)

M _n             max _Ar

Условие для массовой доли кластеров означает, что частицы, оказавшись в пристенном слое, мгновенно исчезают из газового потока, оседая на стенке, т.е. осаждение кластеров определяется их диффузией к стенкам. Инерционным и гравитационным осаждением пренебрегаем. Дуговой разряд полагается точечным и сферически-симметричным, причем в прилежащей дуге области содержится только атомарный пар металла:

U = 0, V = 0, W = 0, T = 2000...3000 K, C L = 1, C L = 0, C L = 0.     (8)

M 1           IM n _#1           Ar

На поверхности вращающегося электрода полагаем выполненными условия непроскальзы-вания и непроницаемости:

U = 0, V = 0, W = to r , d C |_M n /d n = 0, n = 1, N max , d C |Ar /d n = 0.          (9)

В начальном состоянии смесь содержит только атомы аргона при температуре Т = 300 К. Коэффициенты диффузии атомов и кластеров и коэффициент теплопроводности определяются в рамках модели твердых сфер [16].

Микроскопическая модель

Процессы нуклеации в пересыщенном паре в пренебрежении тройными и более столкновениями описываются уравнениями f- = у я

^ pn,m,UmJk , dt здесь fn - концентрация кластеров, состоящих из n атомов, а коэффициенты уравнений Pnmk пропорциональны вероятностям образования кластера размера n в результате столкновения кластеров, состоящих из m и k атомов. Уравнения (10) записаны в предположении, что частота столкновений описывается кинетической теорией идеального газа и может быть определена из концентраций кластеров. В термодинамических теориях проводится учет столкновений кластеров только с атомами (мономерами) и вводится предположение, что все такие столкновения приводят к их слиянию, либо к отделению атома от кластера. В этих обстоятельствах (10) преобразу- ется до d t    Pn, n-1,1 fn-1 f 1   Pn+1, n ,1 fnf 1 + an, n+1,1 fn+1 f 1   an-1, n ,1 fnf 1,

где коэффициенты в пропорциональны вероятности слияния кластера и атома, а а - отделения атома при столкновении кластер-атом. Коэффициенты an-1 n 1 и pn+1 n 1 связаны соотношением

^±l,niL = —n-, где P * - есть давление насыщенного пара над устойчивым зародышем, Pn - над an -1, n ,1    Pn          П кластером, содержащим n атомов [11]. Давления Pn* и Pn определяются по формуле Гиббса– Кельвина, а радиус устойчивого зародыша при данных температуре и пересыщении в ячейке можно рассчитать из зависимости свободной энергии образования кластера-капли от радиуса капли – по абсциссе максимума этой зависимости [17].

Численный метод решения

Учет распределения кластеров по размерам в каждой ячейке камеры проводится аналогично работе [15], где была введена логарифмическая шкала размеров, вдоль которой, согласно формулам (11), происходит миграция кластеров. Решение уравнений (11) проводится явно для всех кластеров из линейки размеров и в каждой ячейке разностной схемы. После перерасчета на единицу времени и объема это дает значения прироста массовой доли и тепловыделения для подстановки в уравнения (3, 5, 6). Решение системы (1)–(9) проводится разностными методами, т.е. разбиением всего рабочего объема на элементы, в объеме которых можно считать температуру, плотность смеси, скорость и массовые доли кластеров и атомов постоянными. Разностная сетка равномерна в цилиндрических координатах, системы разностных уравнений решаются методом исключения Гаусса. Расчеты проведены для меди.

Результаты и обсуждение

На рис. 2, а и б показаны распределения скоростей и температуры, полученные решением системы (1)–(9), (11). Как показали расчеты, наибольшая скорость достигается вблизи дуги. Разлетающиеся от дуги частицы подхватываются круговыми течениями и устремляются к стенке. Расчеты для рис. 2 выполнены при температуре в дуге 3000 К, расход меди составлял 10 мг/с.

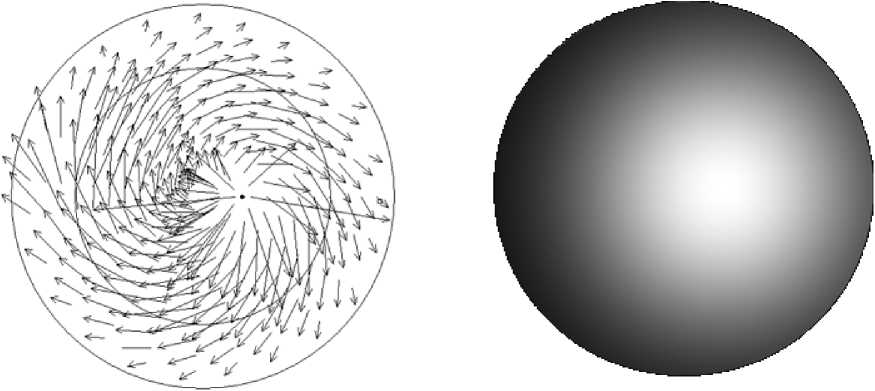
Рис. 2. Поля скорости и температуры в газе вблизи вращающегося электрода. Черной точкой отмечена дуга. Внутренний круг изображает электрод-диск, внешний круг показывает границы камеры

Использование уравнений (11) для каждой ячейки разностной схемы и на каждом временном шаге позволяет получить локальные распределения металлических частиц по размерам. Исходя из этих данных, можно вычислить интегральный диффузионный поток к стенкам камеры и, следовательно, временную эволюцию количества осажденных на стенках частиц. На рис. 3 показаны распределения по размерам осевших на стенках за 10 мкс частиц, полученные при значениях угловой скорости вращения диска 100 и 250 рад/с и температурах в дуге 2000 К и 3000 К. Как видно из рис. 3, во всех случаях формируется сплошное распределение, максимум которого приходится на кластеры малых размеров (1–50 ат.). Распределения тем уже, чем выше угловая скорость вращения диска и чем выше температура в дуге. На рис. 3, в видно формирование второго максимума распределения, приходящегося на частицы, содержащие 10⁴ атомов (около 1 нм). Появление второго горба кривой распределения связано, возможно, с тем, что 10⁴ – это среднее количество атомов, которые могут объединиться в кластер в пути по пересыщенной среде от электрода к стенке, т.е. среднее количество присоединенных атомов. Это отчасти подтверждает факт, что при дальнейшем уменьшении скорости вращения и (или) температуры горб на распределении смещается в сторону больших размеров кластеров, а при увеличении исчезает – сливается с хвостом кривой, имеющей максимум при малых значениях n (рис. 3, а , б ).

Физика

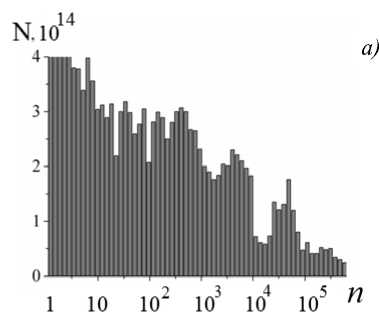
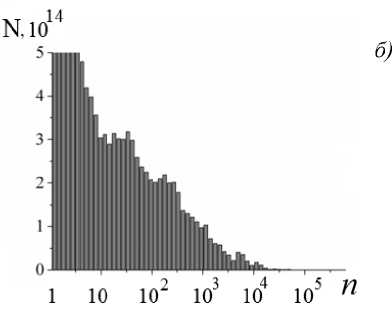
Рис. 3. Распределение по размерам частиц, осажденных на боковой стенке камеры с дуговым разрядом, за

10 мкс: а ) to = 100 рад/с , Т д = 3000 К; б ) to = 250 рад/с ,

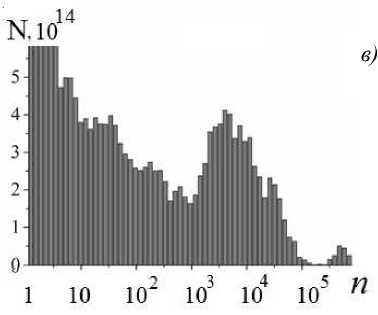
Т „ = 3000 К; в ) to = 100 рад/с , Т д = 2000 К

Заключение

Таким образом, в работе предложена и реализована модель процессов формирования наночастиц меди в процессах испарения-конденсации в камере с дуговым разрядом.

Получены распределения макроскопических (температура, давление, поле скоростей) и микроскопических частиц (распределение кластеров по размерам) в каждой точке рабочей камеры.

Обнаружено, что при температурах в дуге T <  2000 К и скоростях вращения электрода-диска, меньших 100 рад/с, функция распределения кластеров по размерам имеет два максимума, один – в области малых кластеров, другой приходится на кластеры, содержащие более 10⁴ атомов. Появление второго горба кривой распределения связано, видимо, с существованием среднего числа атомов, которые могут присоединиться друг к другу за средний путь от места дугового разряда и до стенок камеры. На это среднее число и приходится второй пик кривой. Полученные результаты не претендуют на количественное совпадение с экспериментом, однако позволяют предсказать эволюцию функции распределения по размерам частиц, осевших на стенках камеры, при изменениях температуры в дуге и скорости вращения электрода-диска.