Математическое моделирование гидрогазодинамических процессов при движении двухфазной среды в кольцевых соплах

В ракетных топливах в качестве добавок к основному горючему используются следующие металлы: алюминий (А1), бериллий (Be), бор (В), магний (Mg), цирконий (Zr), а. также соединения металлов - гидрид алюминия (А1Н3) и ряд других соединений, в частности гидриды упомянутых выше металлов. Применение металлизированных топлив в ракетном двигателе имеет ряд преимуществ по сравнению с безметальными топливными составами: во-первых, позволяет существенно повысить плотность используемого ракетного топлива, и разместить в одном и том же корпусе ракетного двигателя большее количество топлива, во-вторых, величина, удельного импульса, тяги металлизированного топлива, значительно превышает аналогичную величину для топлив без металлических добавок, что обусловливается более высокой энергетической эффективностью химических реакций, протекающих с участием металлизированных добавок и более высокой температурой продуктов сгорания в камере ракетного двигателя.

В продуктах сгорания могут одновременно присутствовать как окислы металла, находящиеся в различных агрегатных состояниях: твердом, жидком и газообразном, так и окислы различных металлов (если в состав металлизированного ракетного топлива, входит несколько металлов или их соединений), которые также могут находиться в различных агрегатных состояниях. Таким образом, течение продуктов сгорания в сопле ракетного двигателя представляет собой течение многокомпонентной (многофазной) среды.

Однако, при использовании металлизированных ракетных топлив в ракетных двигателях, в продуктах сгорания которых присутствуют конденсированные вещества, возникает

А.Л. Карташев, М.А. Карташева ряд специфических проблем без решения которых невозможно эффективное использование рассматриваемых топлив в реальных конструкциях.

Во-первых, наличие в продуктах сгорания частиц конденсированной фазы приводит к тому, что в потоке имеет место скоростная и температурная неравновесность параметров газовой и конденсированной фазы, приводящая к снижению удельного импульса тяги. Во-вторых, различие в траекториях движения газа и частиц конденсированной фазы приводит к осаждению частиц на поверхности сопла, которое также приводит к потерям удельного импульса тяги вследствие передачи (частично или полностью) импульса частиц стенкам соплового блока. Кроме того, такое осаждение может вызвать интенсивную эрозию профилированных обтекаемых поверхностей сопла и привести к их значительному искажению, что приводит к нарушению расчетного режима течения в сопле, либо к полному или частичному его разрушению. Все упомянутые эффекты характерны для сопел всех видов, в том числе сопел Лаваля и кольцевых сопел.

Исследование гидрогазодинамических процессов в кольцевом сопле, прежде всего движения конденсированной фазы, находящейся в жидком либо твердом состоянии, и определение параметров этого движения представляет основную задачу с точки зрения определения эффективности кольцевого сопла [1]. Наличие в потоке частиц конденсированной фазы приводит к возникновению в сопле эффектов, непосредственно влияющих на газодинамические и тяговые характеристики сопла и его работоспособность в составе газодинамических устройств различного назначения.

Рассматривая движение конденсированной фазы в кольцевых соплах, необходимо исследовать параметры движения двухфазной среды, состоящей из газообразной несущей фазы и конденсированной фазы, представляющей собой твердые частицы либо жидкие капли. В этом случае конденсированная фаза может представлять собой различные вещества, каждое из которых может находиться как в твердом, так и жидком агрегатном состоянии. Наличие химических реакций и фазовых переходов в двухфазной смеси, истекающей из кольцевого сопла, приводит к изменению параметров смеси по тракту сопла, что еще более усложняет картину течения в кольцевом сопле.

Задача определения параметров движения двухфазной смеси в кольцевом сопле представляет, таким образом, сложную комплексную задачу, включающую в себя исследование гидрогазодинамических, физических, химических процессов при наличии существенных градиентов исследуемых параметров.

Итак, двухфазный поток в кольцевом сопле характеризуется следующими основными особенностями:

• -    наличием значительных градиентов газодинамических параметров, особенно в окрестности кольцевого минимального сечения сопла, определяющих структуру течения в сопле;

• -    наличием существенной скоростной и температурной неравновесности двухфазного потока, приводящей к значительным потерям тяги;

• -    интенсивным осаждением частиц из потока на внутренние обтекаемые поверхности сопла, что, в свою очередь, вызывает снижение тяги из-за передачи части импульса стенкам сопла;

• -    наличием эрозионного воздействия частиц конденсированной фазы на обтекаемые профилированные поверхности (внешнюю обечайку и центральное тело) кольцевого сопла, вызывающего искажения этих поверхностей и снижение удельного импульса тяги;

• -    присутствием в многокомпонентном потоке фазовых переходов и химических реакций.

Решение задачи определения тяговых характеристик кольцевого сопла с двухфазным рабочим телом с учетом всех указанных особенностей может быть осуществлено с помощью математического моделирования, включающего разработку математической модели рассматриваемого явления, реализацию ее в виде численного алгоритма и проведение чис-

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ленных исследований газодинамических и тяговых характеристик сопла.

Основная задача исследования характеристик кольцевого сопла, как уже было отмечено выше, заключается в определении его тяговых характеристик. Тяга сопла может быть определена путем расчета термодинамического импульса тяги и потерь удельного импульса тяги, обусловленных двухфазностью потока.

Расчету течений двухфазных потоков, в том числе в соплах различных типов, посвящено достаточно большое количество научных работ, развернутый обзор которых проведен в работе [2]. В ней, в частности, отмечается, что для расчета трансзвуковых течений нашел применение метод установления, при использовании которого сложная краевая задача для эллиптично-гиперболической системы уравнений сводится к более простой краевой задаче для гиперболической системы уравнений с большим количеством переменных. Применительно к течениям газа с частицами в соплах, этот метод для решения прямой задачи в ее точной постановке реализован в работах [2, 3].

Один из вариантов рассматриваемого подхода заключается в разбиении исходной системы уравнений на две группы: уравнения для газа и уравнения для частиц. При этом уравнения для газа решались методом установления, а уравнения для частиц, вследствие их гиперболичности во всей области течения, решались для стационарного потока. Решение системы уравнений, описывающей движение двухфазной смеси в данном случае, удобно проводить путем ее разбиения на подсистему газа и подсистему частиц, связь между которыми осуществляется только через правые части уравнений, описывающие процессы взаимодействия газа и частиц.

В данной статье рассматривается осесимметричное движение двухфазной среды при исходных допущениях, представленных в работах [4, 5] (впервые предложены Клигелем в работе: Kliegel J.R. One-dimensional Flow of Gas-Particle System. - IAS Paper, 1960, № 5, 20 p.):

• -    среда является двухскоростной и двухтемпературной, то есть в каждой точке двухфазного потока существуют две скорости и две температуры - скорость и температура газа и частиц;

• -    совокупность частиц принимается непрерывно распределенной по всему объему с плотностью ps, равной отношению массы частиц в рассматриваемом объеме к величине этого объема;

• -    течение стационарное, массовый расход газа и частиц вдоль по течению постоянны;

• -    давление создается только газом, влиянием частиц можно пренебречь;

• -    частицы являются сферами одинакового размера и не взаимодействуют между собой и со стенками сопла;

• -    система теплоизолирована, теплообмен между частицами и газом осуществляется только путем конвекции;

• -    объемом, занимаемым частицами, а также гравитационными и электрическими силами можно пренебречь;

• -    вязкие силы проявляются только при взаимодействии частиц с газом, ускорение частиц обусловлено действием этих же сил;

• -    вследствие высокой теплопроводности материала частиц их температура постоянна по всему объему частиц;

• -    газ является идеальным, химически не реагирующим, а теплоемкость газа и частиц постоянны.

Поставлена задача математического моделирования гидрогазодинамических процессов при движении двухфазных монодисперсных потоков в кольцевых соплах внешнего расширения (в том числе с укороченным центральным телом) при комплексном учете всех основных особенностей рассматриваемого потока.

А.Л. Карташев, М.А. Карташева

Двухфазное монодисперсное течение в кольцевом сопле описывается системой уравнений осесимметричного течения двухфазной смеси в интегральной форме [1, 4], позволяющая вести « сквозной » счет без предварительного выделения разрывов в расчетной области. Система записана для плоскости сечения X,Y для фиксированной пощади а, ограниченной контуром Г:

^ JI pydxdy + I py ( udy — vdx ) = 0;

σ Γ

It Ц psydxdy + Г psy (Usdy — Vsdx) = 0; σ дШ*"^ у/[„.№++ σσ

I y (( P + pu 2) dy — puvdx ) = 0;

Γ

^д Ц pvydxdy + Iy у (p_sfy — |^ dxdy + I y ( puvdy — ( p + pv ²) dx ) = 0;

σ

σ

σ

σ

^dJj_№^ydxdy -jffydxddy ⁺

σ

σ

Γ

I yp_su_s ( Usdy

Γ l ypsVs (Usdy

Γ

— vsdx ) = 0;

— vsdx ) = 0;

dit Ц РУ (V r + ^e) dxdy + / [ Psy ( Vs ■ f + q ) dxdy + ^ РУ ( V + ^ ( udy — vdx ) = 0;

σ

σ дЩ psesydxdy — j^ psqydxdy +

σ

σ

Γ

I psesy ( Usdy — Vsdx ) = 0 ,

Γ

где p и p_s - плотноети газа и « газа » частиц; p - давление газа; u и v - осевая и радиальная компоненты вектора скорости газа V; us и vs - осевая и радиальная компоненты вектора скорости частит! Й д x п y - осевая и радиальная координаты: e = e ( p,T )- удельная внутренняя энергия газа; e_s = e_s ( T_s ) = свT_s - удельная внутренняя энергия вещества частиц, св ~ удельная теплоемкость вещества частиц; p = pRT - уравнение состояния совершенного газа: t - время: f = dVts; q = des.

Необходимо отметить, что при записи вышеприведенной системы уравнений считалось, что объем, занятый частицами конденсированной фазы, мал, и им можно пренебречь, и влияние частиц в создании давления среды пренебрежимо мало. Давления газа и конденсированной фазы совпадают.

Расчет поля течения осуществляется методом установления с использованием вычислительного алгоритма, построенного на основе разностной схемы С.К. Годунова - В.П. Колгана [1, 6, 7]. Граничные условия системы уравнений приняты следующими:

• -    на жестких стенках принято условие непротекания vn = 0;

• -    на входной дозвуковой границе: энтропия S=const, полная энтальпия H о = const; распределение угла наклона вектора скорости 0 * = 0 * ( x,y ).

Выходная граница, выбрана, так, чтобы нормальная к границе компонента, скорости была, бы сверхзвуковой, в этом случае постановки граничных условий не требуется.

Параметры частиц на входной границе us, vs, Ts совпадают с соответствующими параметрами газовой фазы.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Алгоритм расчета двухфазных монодисперсных потоков в кольцевых соплах реализован в модулях расчета параметров движения двухфазной монодисперсной смеси в до-, трансзвуковой области течения и в сверхзвуковой области течения, который отличается особенностями вычислительного алгоритма, связанными с гиперболичностью системы уравнений во всей рассматриваемой области течения, и использованием, в связи с этим, вместо схемы С.К. Годунова - В.П. Колгана модифицированной маршевой схемы М.Я. Иванова -А.Н. Крайко - Н.В. Михайлова.

Определение потерь удельного импульса тяги из-за скоростной и температурной нерав-новесности потока проведено путем сравнения результатов расчета параметров двухфазного потока и параметров течения газового потока. Однако, для того, чтобы прогнозировать величину потерь тяги кольцевого сопла на стадии предварительных исследований его характеристик, необходимо исследовать влияние параметров газовой и конденсированной фазы на величины, характеризующие работу сопла.

Для оценки потерь удельного импульса тяги двухфазного потока необходимо исследовать зависимости величин тяги R и расхода рабочего тела G через кольцевое сопло от таких параметров конденсированной фазы как размер частиц <1, концентрация частиц п, массовая доля z. Указанные параметры конденсированной фазы выражаются через параметры, входящие в систему уравнений (1).

С помощью разработанного вычислительного алгоритма проведены численные исследования величин тяги и расхода в кольцевом сопле рассматриваемой конфигурации с целью определения влияния параметров конденсированной фазы на вышеупомянутые характеристики сопла и определения параметров конденсированной фазы, при которых тяга R и расход газа G через сопло максимальны [1].

Для проведения математического моделирования рассмотрена типичная конфигурация кольцевого сопла (рис. 1) со следующими геометрическими параметрами, обезразмеренны-ми на величину радиуса, на котором находится нижняя граница, кольцевого минимального сечения:

• -    ширина минимального сечения h = 0 , 2;

• -    угол наклона минимального сечения к оси сопла 0 * = 40 °;

• -    длина сопла, Lc = 1 , 65;

• -    радиус выходного сечения сопла Ra = 1 , 57 .

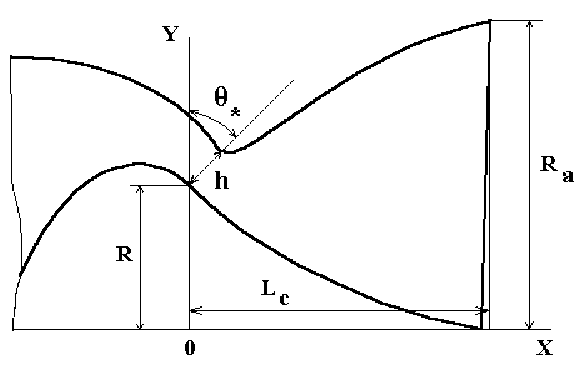
Рис. 1. Схема, кольцевого сопла, для параметрических расчетов

В качестве конденсированной фазы рассмотрены сферические частицы диаметром d = 1 — 10 мкм, массовая доля которых в двухфазной смеси z изменялась от 0,05 до 0,5.

А.Л. Карташев, М.А. Карташева

Параметры газовой фазы приняты следующими:

• -    давление газа на входе в сопло po = 10 МПа ( ~ 100 атм);

• -    температура газа на входе в сопло To = 3000 К;

• -    показатель изоэнтропы газа к = 1 , 25;

• -    коэффициент динамической вязкости ц = 9 , 5 • 10 ~ ⁵ (кг/м - с).

Число Прандтля Pr принято равным 0,75, характерный размер для расчета числа Рейнольдса Re принят равным ширине щели кольцевого критического сечения и составляет ~ 0 , 05 м.

В результате численных параметрических исследований получены следующие характеристики течения в кольцевом сопле типичной конфигурации (см. рис. 1):

• -    'зависимость Ни G от диаметра частит; d при фиксированном значении z (рис. 2);

• -    'зависимость Н и G от массовой доли z при (фиксированном значении d (рис. 3):

• -    'зависимость Н и G от диаметра частиц d при (фиксированном значении n (рис. 4).

  

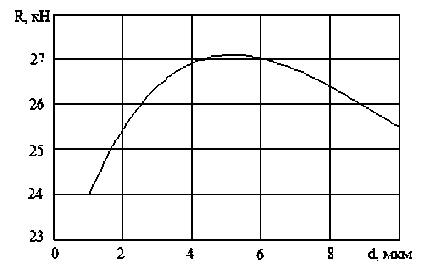
  Рис. 2. Зависимость R и G от диаметра частиц d при z = 0 , 3

  
  
  
  
  
  

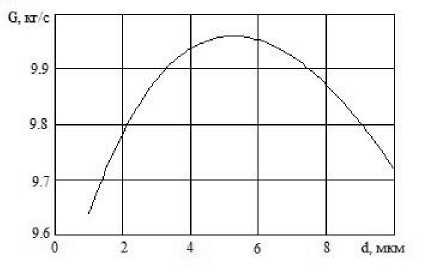
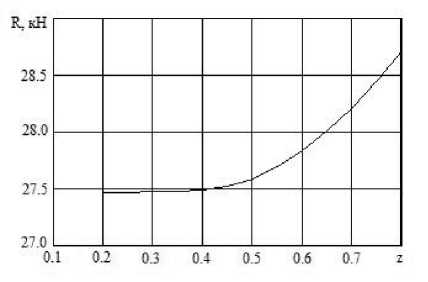
  Рис. 3. Зависимость R и G от массовой доли конденсированной фазы z при d = 5 мкм

  
  
  
  
  

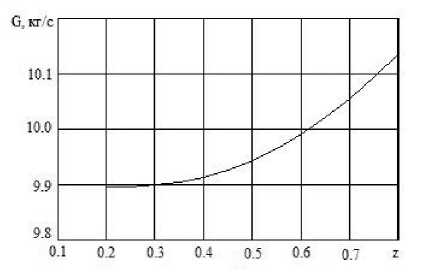
Анализ полученных результатов позволяет сделать следующие выводы. Установлена величина диаметра частиц конденсированной фазы, при котором значения тяги и расхода газа достигают своего максимального значения при фиксированной доле конденсированной фазы в двухфазном потоке, для данной конфигурации сопла и принятых параметрах рабочего тела эта величина составила ~ 5 мкм. Зависимости тяги и расхода от z при фиксированном диаметре частиц (в данном случае рассмотрены частицы с диаметром d = 5 мкм) и зависимости тяги и расхода от диаметра частиц d при постоянной концентрации частиц конденсированной фазы, в отличие от предыдущего случая, носят монотонный характер. При этом обнаружена существенная особенность этих зависимостей: слабое изменение тяги

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

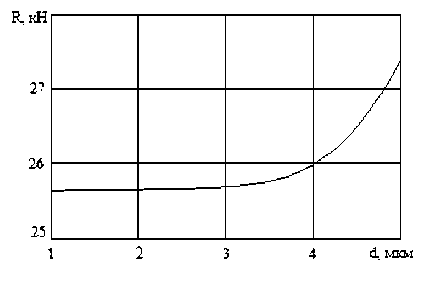
Рис. 4. Зависимость R и G от диаметра частиц d при n = const

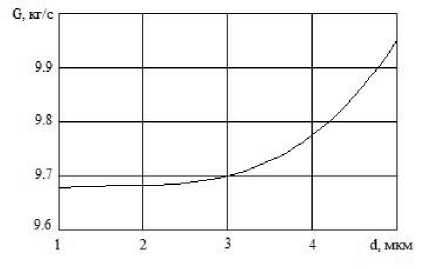
и расхода при изменении диаметра частиц от d ~ 1 мкм до d ~ 3 мкм (при n = const) и существенный рост тяги и расхода при увеличении диаметра частиц свыше 3 мкм. И аналогичный характер зависимости тяги и расхода от массовой доли конденсированной фазы z (при d = 5 мкм): слабый рост исследуемых параметров при изменении массовой доли от z ~ 0 , 1 до z ~ 0 , 5 , и существенный рост тяги и расхода, при увеличении z свыше 0.5.

Полученные результаты и установленные закономерности позволяют определить величины R и G для различных параметров газа и конденсированной фазы и спрофилировать кольцевое сопло с центральным телом и внешней обечайкой, обеспечивающее заданные тяговые характеристики.

Несмотря на. то, что в реальном сопле ракетного двигателя наличие монодисперсного конденсата, маловероятно, исследования двухфазных монодисперсных потоков играют важную роль с точки зрения исследования поведения частиц конденсированной фазы, влияния ее параметров (диаметра, частиц, массовой доли в продуктах сгорания и т.п.) на. характеристики движения двухфазного рабочего тела, в сопле и тяговые характеристики сопла.

Естественно, что результаты аналогичных параметрических исследований, проведенные при других геометрических характеристиках кольцевого сопла, и параметрах рабочего тела, могут несколько отличаться от результатов параметрических исследований, приведенных в данном исследовании. Это обусловлено тем, что число возможных варьируемых параметров при параметрических исследованиях течений двухфазных монодисперсных сред превышает число возможных варьируемых параметров при исследованиях течений чистого газа.

Необходимо отметить еще одну особенность численного моделирования течений в кольцевых соплах при наличии в рабочем теле конденсированной фазы, которая была, обнаружена. в ходе параметрических исследований. Для проведения численных исследований в настоящем исследовании была, выбрана, конфигурация полноразмерного кольцевого сопла, смешанного расширения с внешней обечайкой и центральным телом. Рассмотренную конфигурацию можно назвать « гладкой » . Математическое моделирование течений в других, « негладких » , конфигурациях кольцевых сопел, показало наличие значительных вычислительных трудностей, возникающих при расчете характеристик таких конфигураций [1]. В этом случае при исследовании характеристик кольцевого сопла, внешнего расширения с укороченным центральным телом за. торцем центрального тела, происходит пересечение траекторий частиц конденсированной фазы. Для разрешения возникающей особенности можно рассмотреть возникающую в потоке поверхность (в рассматриваемом осесимметричном случае она представляет собой « шнур » ), которая имеет название « пелена » и модели расчета которой представлены в работе [2]. Решение, получаемое на. пелене частиц, будет влиять только на. параметры донной области, которые определяют величину тяги, создаваемой торцем укороченного центрального тела. Учитывая, что величина, тяги торца, невелика, по

А.Л. Карташев, М.А. Карташева сравнению с величиной тяги, определяемой профилированным укороченным центральным телом, такое пересечение траекторий в рассматриваемой области течения, приводящее к существенному усложнению вычислительного алгоритма, рассматривать нецелесообразно.