Математическое моделирование и эконометрический анализ процесса сгорания композиционного топлива

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 004.912+662.659                              

В настоящее время разработка способов решения глобальных экологических проблем, таких как изменение климата, загрязнение атмосферы, является одной из наиболее актуальных проблем. Согласно статистическим данным по мировым показателям экологической эффективности (EPI) и чистоты воздуха (IQAir), Кыргызстан занимает 126-е место из 180 стран по состоянию окружающей среды, 19-е место из 100 стран по степени загрязнения воздуха. Плохое качества воздуха представляет серьезную угрозу для жизни людей. Согласно данным Всемирной организации здравоохранения за последние 10 лет часто фиксируется респираторные заболевания (астма аллергического типа, бронхолегочные, сердечно-сосудистые осложнения).

Одним из основных источников загрязнения воздуха является уголь, используемый для отопления жилья. Сжигание угля в котельных ТЭЦ осуществляется по устаревшим технологиям, в результате приводит к серьезным экологическим проблемам.

Таким образом, возникает необходимость разработки эффективных технологий использования угля. Одним из способов решения обозначенных сложностей является сжигание угля в виде водоугольного топлива (ВУТ) [1].

Анализ результатов представляет перспективность использования водоугольного топлива, однако на сегодняшний день имеются нерешенные следующие проблемы:

– увеличение калорийности частицы ВУТ;

– компьютеризация процессов приготовления, транспортировке, хранения и сжигания ВУТ.

В основном исследователи структурируют процесс сжигания частицы ВУТ на 4 этапа:

прогрев, испарение влаги, выход и сгорание летучих веществ, выгорание углерода. На основе экспериментальных исследований, проведенных Б. В. Канторовичем и Г. Н. Делягиным [2, 3], были сделаны следующие выводы:

• –    ВУТ имеет высокую реакционную способность;

• –    вода имеет большое влияние на процесс воспламенения и горения частицы ВУТ.

Изложенные выше характеристики принимаются во внимание при моделировании горения частицы ВУТ и определяет актуальность следующей задачи.

Постановка задачи

Исследуется система «частица ВУТ — высокотемпературный газ». Частица ВУТ попадает в поток высокотемпературной среды. Тепловой поток подводится равномерно к поверхности частицы. Под влиянием высокотемпературного потока происходит в системе: прогрев частицы, испарение влаги, термическое разложение органической части угля и выход летучих, газофазное воспламенение, зажигание кокса [4].

Здесь следует отметить, что все вышеуказанные процессы протекают одновременно.

Таким образом, целью данной статьи является исследование процесса сгорания частицы ВУТ и разработка математической модели процесса. Схема области решения поставленной задачи отображена на Рисунке 1.

Для решения поставленной задачи примем следующие допущения:

• –    теплофизические характеристики ВУТ постоянны, т. е. не зависят от координат и времени;

• –    теплообменный процесс внутри частицы одномерен, т. е. теплота распространяется в одном направлении;

• –    тепло распространяется конвекцией и излучением;

• –    взаимодействие воды с углеродом не принимается во внимание;

• –    тело частицы ВУТ имеет сферическую форму.

  

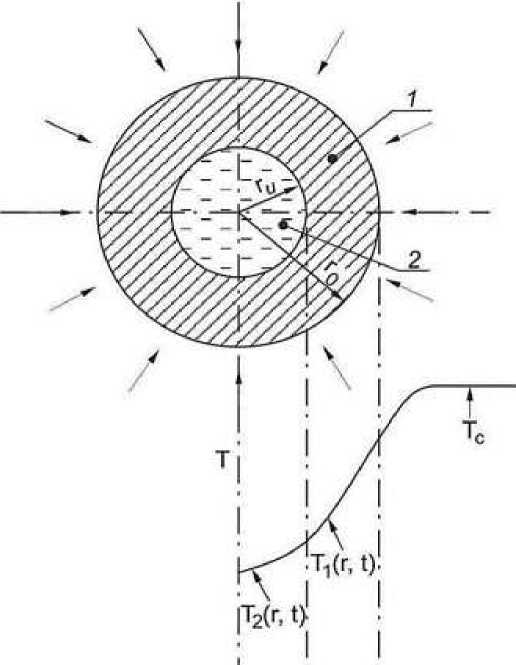
  Рисунок 1. Схема области решения задачи. 1. Сухой слой. 2. Исходная ВУТ.

  
  

Схема, представленная на Рисунке 1, является физической моделью данной задачи. Исследование любого физического явления приводится к выявлению корреляцию между величинами, описывающими данное явление. Математическая модель для системы «частица ВУТ — высокотемпературный газ», соответствующая этой схеме, основана на системе уравнений [5]:

• — уравнение энергии для сухой части ^

  дТ 1 (г, t) dt

  
  

д2Т1(г,{)  1дТ1(г,{)               Q„^k0     ,      Е

= “1 [-Зт2Г- + 7~dT~\+ (1- ^(г' t))-c;Г'exp(-R■T1(г,t))

t>0,    ги<г <г1,    Ти< Т,

— уравнение химической кинетики для угольной компоненты топлива

дЛ1(г,^)                Qхим•k0             Е

—(1-^(г^—с;г'ехр(-r^^ t>0,    ги<г <г1,    Ти< Т,

— уравнение энергии для исходной части топлива

дТ2(г, t) dt t> 0,

= “2 [

д2Т2(г, t) дг2

0 < г < ги,

+ 1dT2(r,t)1 г дг

Ти<Т,

с начальными (Т(г, 0) = Т₀) и граничными условиями:

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №4. 2024

dT^r^t)

-2i    dr = “[Гс - Ti(r°,f)] + £ • ^ [T44 — T4(r°, f)]

граничные условия четвертого рода на границе испарения

dTi(r,t)

1 dr

^| г=г_и+°

dT2(r, t) Л2^-^ I dr

•_и-°    С исп ^ исп ,

Ti(rK,t) = T2(rK,t) = TK,

dTi(0,t) =Q dr

Здесь, T° — начальная температура частицы, К; T_c — температура окружающей среды,

К; Г и

—

пространственная координата границы испарения, м; ст = 5,67 • 10 ⁸ -Вт— — м² К⁴

константа излучения абсолютно черного тела, а 1 — коэффициент температуропроводности исходной части ВУТ, м-; а₂ — коэффициент температуропроводности сухой части ВУТ, м-; 2 1

—

коэффициент теплопроводности исходной части ВУТ, Вт ; 2₂

мК '

—

коэффициент

теплопроводности сухой части ВУТ, Вт; %сп — массовая скорость испарения, -г-; фисп

—

мК      п                                             м2с      п тепловой эффект испарения, Вт; фхим — тепловой эффект реакции термического разложения, кг к° — предэкспонент химической реакции, £ — степень черноты частицы ВУТ, E — энергия активации, п — степень превращения, R = 8,31  ^ — — универсальная газовая постоянная.

Координата границы испарения находилась из решения системы уравнений (1)-(4) с учетом граничных условий (5)-(7) по формуле: ^ = Т| — f Vk • dr, где VЖ = ^исп— линейная

РЖ скорость продвижения фронта испарения, -. Скорость испарения находилась по формуле:

^исп = V° • ехр(-

■ ^Q иcп ■p■^(T 1   ^T 0 )

R-T 0 -T 1

■), где T 1 — температура на границе испарения, V ° — скорость

испарения при температуре замерзания, ц — молярная масса водяного пара.

Численная модель задачи

Созданная математическая модель решалась численным методом конечных элементов с помощью программы Elcut, и разработана компьютерная модель. В работе проведено двумерное численное моделирование. До начала моделирования следует оценить теплофизические характеристики влажной и «обезвоженной» части топлива (уголь марки «Д») и поэтому были определены с учетом объемных долей основные параметры:

Вт           Дж

T° = 300^(26,85°С), Tc = 1173,15 оК(900°С), 22 = 1655^^, с2 = 2426^^, р = 1630кг, а = (100 ^ 500)^т-,0 <£< 1, ст = 0,0000000567,   r0 = 1500мкм.

м3                 м2 оК

Т. е. начальная температура частицы T 0 и температура окружающей среды T c соответственной равны 300 °K и 1173 °K.

Решение задачи

При моделировании процесса горения температура окружающей среды и диаметр частицы ВУТ соответственно варьировались в значительно широком интервале (870–1500 °K), (1000–3500 мкм). Корректность математической модели, характеризующей исследуемый процесс, была проверена путем проведения вычислительного эксперимента в созданной компьютерной модели. Также результаты экспериментов, выполненных учеными, были подтверждены результатами, полученными на модели, созданной в программе Elcut. Результаты проведенных исследований представлены на Рисунках 3–5.

С целью определения факторов, влияющих на процесс горения, и оценки уровня зависимости между ними создана регрессионная модель изучаемого процесса. В результате линейная модель множественной регрессии была определена следующим образом:

Y = 301,9 - 1,59 • %! + 27096 • %2 + 0,338 • %3 + 0,337 • %4 (8)

где, %1 — время воспламенения, %2 — диаметр частицы ВУТ, %3 — температура окружающей среды, %4— температура частицы ВУТ через 1 секунду, Y — стабильная температура в процессе горения.

Проверка корректности регрессионной модели осуществлялась исследовательским и подтверждающим анализом. Результат можно представить графически, Рисунок 2.

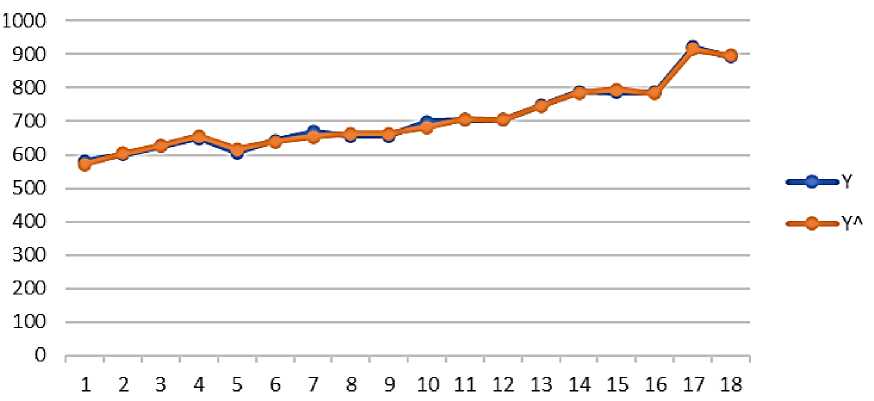
Рисунок 2. Проверка корректности регрессионной модели

Результаты численных расчетов

На Рисунках 3, 4 и в Таблице приведены результаты расчетов для всех трех использованных граничных условий для температуры (5), (6) и (7). Полученные результаты представлены в виде зависимости скорости изменения температуры от времени на поверхности частицы. На Рисунке 4 представлен градиент температуры в сферической частице.

Результаты и обсуждения

Из полученных данных, представленные на Рисунке 3 и Таблицы видно, что температура на поверхности частицы через 1 секунду становится равной 110,12 °C, а через 14 сек 598,38 °C.

Сравнение полученных результатов численным методом конечных элементов с помощью программы Elcut с экспериментальными данными работ [1–4], показывают, что погрешность составляет в среднем 5% и свидетельствует о физической обоснованности математического моделирования рассматриваемой задачи. Таким образом, использование программы Elcut позволяет моделировать рассматриваемый класс задач с достаточной точности.

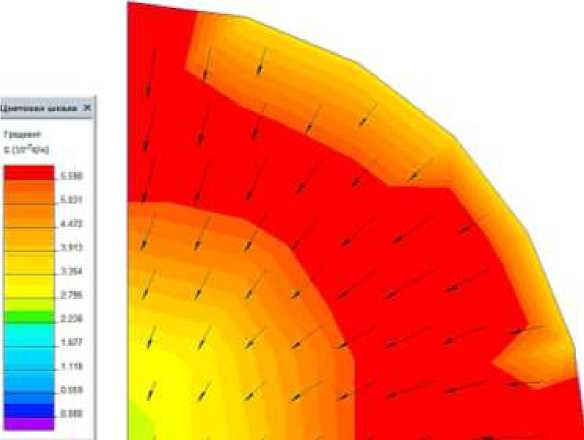
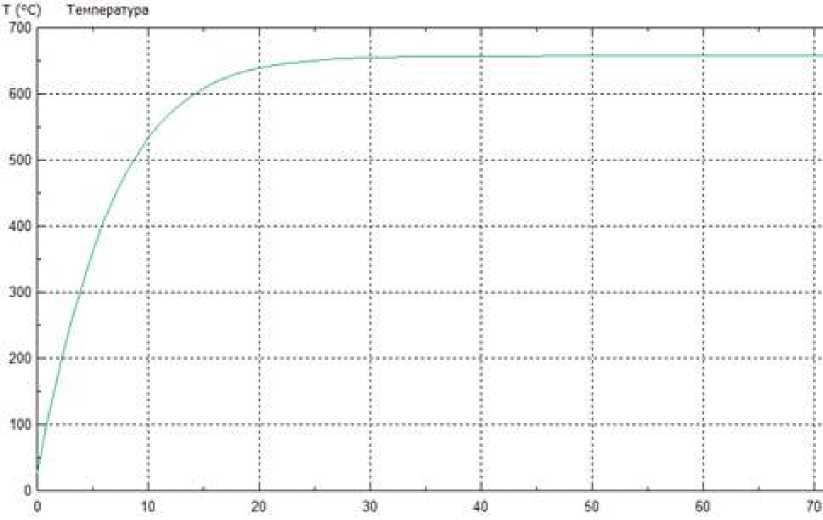
Рисунок 3. Скорость изменения температуры в зависимости от по времени нагрева за счет конвекционного потока

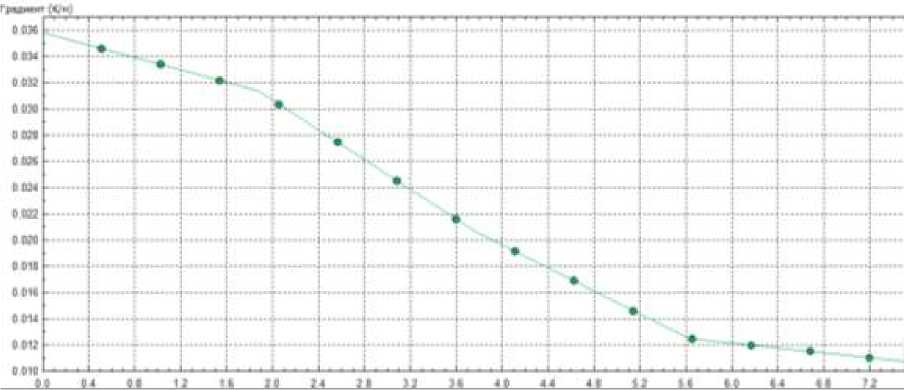
Рисунок 4. Градиент температуры

Таблица

РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ПОВЕРХНОСТИ ЧАСТИЦЫ

Время И	тго	G (К/м)	Gr(К/м)	Gj (К/м)	F (Вт/м2)	Fr (Вт/м2)	Fj (Вт/м2)	I (Вт/К-м)
0	26.85	0	0	0	0	0	0	1655
1	110.184	34.0501	-34.0427	0.710209	56353	-56340.7	11175.4	1655
г	184.823	30.4985	-30.4919	0.636037	50475	-50464	1052.64	1655
3	251.308	27.1668	-27.1609	0.566555	44961	-44951.3	937.649	1655
4	310.157	24.0464	-24.0412	0.501479	39796.8	-39788.1	829.947	1655
5	361.89	21.1388	-21.1342	0.440841	34984.6	-34977	729.592	1655
5	407.046	18.4515	-18.4475	0.384798	30537.2	-30530.6	636.841	1655
7	446.186	15.993	-15.9896	0.333527	26468.5	-26462.7	551.987	1655
3	479.883	13.7689	-13.7659	0.287144	22787.6	-22782.6	475.224	1655
9	508.711	11.7795	-11.777	0.245656	19495.1	-19490.9	406.561	1655
10	533.232	10.0195	-10.0174	0.208952	16582.3	-16578.7	345.816	1655
11	553.981	8.47844	-8.4766	0.176813	14031.8	-14028.8	292.626	1655
12	571.458	7.14155	-7.13999	0.148933	11819.3	-11816.7	246.484	1655
13	586.121	5.99141	-5.99011	0.124947	9915.79	-9913.63	206.788	1655
14	598.38	5.00914	-5.00805	0.104463	8290.13	-8288.32	172.885	1655

Выводы

• 1.    Для анализа процесса сгорания композиционного топлива были использованы методы «Математическое и компьютерное моделирование» и «Регрессионный анализ».

• 2.    На основе численных расчетов рассмотрен процесс сгорания частицы ВУТ и определены основные факторы, влияющие на процесс, установлены зависимости между ними. Созданная в результате исследования регрессионная модель может быть использована для эконометрического прогнозирования процесса сгорания композиционных топлив.

• 3.    Сравнение полученных результатов численным методом конечных элементов с помощью программы Elcut с экспериментальными данными работ [2–4], показывают, что погрешность составляет в среднем 5% и свидетельствует о физической обоснованности уравнений и граничных условий (1)–(7) для математического моделирования расматриваемой задачи и использование программы Elcut для численного расчета.