Математическое моделирование и оптимизация магнитной характеристики инициирующего устройства космического аппарата

В современной космической отрасли существует множество космических аппаратов (КА), которые можно квалифицировать по выполняемым функциям. К этим функциям относятся: дальнее зондирование Земли, наблюдение за дальним космосом, изучение гравитационного поля Земли, передача данных на большом расстоянии, а также многое другое. Осуществление данных функций напрямую зависит от сверхчувствительного оборудования, требования к которому постоянно повышаются 190 по мере роста запросов на более точные результаты измерений или на минимизацию потерь передаваемого сигнала. Это делает современные КА крайне уязвимыми к вибрационным и ударным нагрузкам и, соответственно, ставит задачу преодоления их негативного воздействия.

Основными источниками ударной нагрузки на борту КА являются подпружинные механизмы, суть которых состоит в освобождении подвижных элементов конструкции, и пиротехнические инициирующие устройства (ИУ) [1], используемые для расфиксации тяг, предотвращающих механические устройства, такие как системы раскрытия и зачековки солнечных батарей и рефлекторов, а также устройство отделения КА, от срабатывания. К недостаткам пироустройств также относятся: одноразовость, высокий уровень запыления продуктами горения области КА, сложность наземной отработки из-за высоких требований к предотвращению несанкционированного срабатывания. Наличие указанных недостатков приводит к отказу от подобных устройств в космической отрасли и росту интереса к ИУ с низким ударным воздействием, в частности тепловым ИУ на основе парафина, элементов памяти формы, перегораемых элементов, жидких металлов и высокоплавкого клея [2].

Общей проблемой таких ИУ является увеличение времени срабатывания [2], что приводит к росту нагрузки на бортовую сеть, следствием чего может стать повреждение кабельной сети [3]. В связи с этим возникает потребность в устройстве, способном обеспечить достаточно высокую скорость срабатывания при минимальных ударных нагрузках.

Для решения подобной проблемы применяются устройства с пережигаемыми элементами [4; 5], принцип работы которых состоит в использовании нихромовой нити, которая удерживает фиксатор исполнительного элемента и, имея высокое удельное сопротивление, разрушается при подаче через нее электрического тока. Главным недостатком данных устройств является наличие подпружинного элемента, который создает ударное воздействие. Поэтому в целях сведения ударного воздействия к минимуму предлагается использование

Том 9

ИУ магнитного типа, безударные характеристики которого обеспечиваются индуцируемыми токами. Данный принцип активно применяется в магнитных демпферах [6–9], а также устройствах токовихревых тормозов [10–12].

Основной проблемой устройств данного типа является относительно большая масса, что приводит к необходимости проведения многоцелевой оптимизации изделия в целях достижения максимальной удельной рабочей характеристики при минимальных массово-габаритных значениях и удовлетворения требований прочности. Осуществление оптимизации, в свою очередь, невозможно без получения математической модели основной характеристики устройства от конструктивных параметров.

Учитывая сложность аналитического решения данной задачи, предлагается построение математической модели рабочей характеристики на основе использования метода конечных элементов (МКЭ) и алгоритма машинного обучения. В качестве оптимизационного алгоритма для выполнения многоцелевой оптимизации предлагается использовать алгоритм из теории игр. Данные алгоритмы уже применяются в оптимизации элементов конструкции летательных аппаратов [13; 14], а также магнитных устройств [15].

Целью данной работы является разработка электромагнитного инициирующего устройства с оптимальными массогабаритными параметрами, способными обеспечить высокое время срабатывания при минимальных удельных нагрузках.

1.    Описание изделия

Проектируемое изделие представляет собой соленоид, установленный в магнитопровод, имеющий вид железного корпуса цилиндрической формы, в центре которого расположен нагружаемый элемент, состоящий из сердечника, токопроводящей оболочки сердечника и алюминиевой втулки. В случае подачи постоянного тока через соленоид электрическая энергия будет преобразована в магнитную, что приведет нагружаемый элемент в движение по шариковой втулке вдоль оси z . При прекращении подачи тока нагружаемый элемент возвращается в первоначальное положение под воздействием упругого элемента, который входит в зацепление с алюминиевой втулкой. В качестве упругого элемента может использоваться обыкновенная цилиндрическая пружина сжатия. Принципиальная схема устройства представлена на рисунке 1.

Особенностью изделия является наличие токопроводящей оболочки сердечника. При протекании через нее магнитного потока в ней индуцируются токи, которые создают магнитное поле, имеющее противоположную направленность по отношению

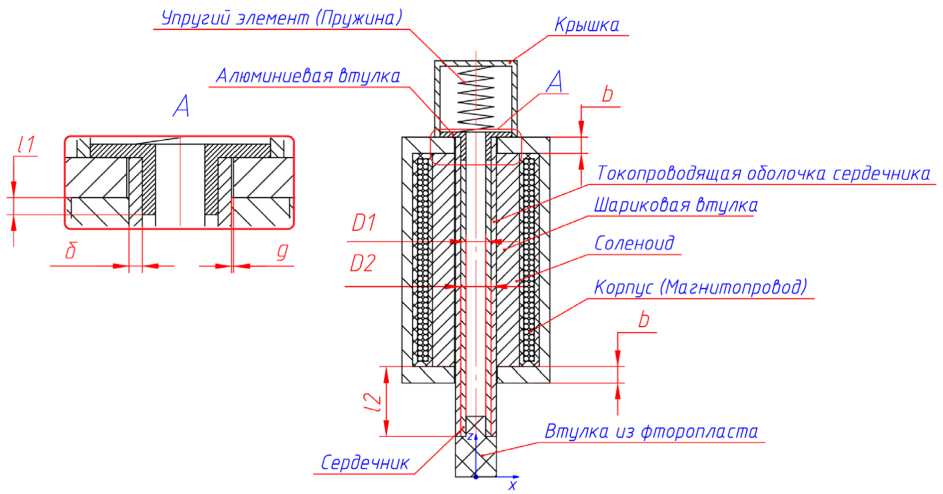
Рисунок 1. Принципиальная схема устройства

к внешнему полю. В результате возникает тормозящая сила, что прямо пропорционально скорости тока. Подобная закономерность позволяет, при верном подборе соответствующих параметров, добиться условий работы, когда устройство имеет высокую скорость срабатывания, при этом ударная нагрузка сведена к минимуму. Общее уравнение движения имеет следующий вид:

ma = Fm - Fb - Ff - Fs, где m – масса исполнительного элемента a – вектор ускорения исполнительного элемента; Fm – сила втягивания сердечника в область соленоида, Fb – сила, генерируемая индуцируемыми токами; Ff – сила сухого трения трущихся элементов; Fs – сила упругости пружины.

Исходя из данного уравнения видно, что основной рабочей характеристикой, обеспечивающей необходимые требования надежности, является генерируемая соленоидом сила F _m, которую для простоты в дальнейшем будем называть магнитной силой. Данный факт ставит задачу получения максимального значения магнитной силы при минимальных массово-габаритных характеристиках и удовлетворений требований прочности, что представляет собой сложную многоцелевую оптимизацию.

2.    Параметрический анализ модели

Для осуществления оптимизации изделия необходимо определить основные конструктивные параметры.

Согласно общему уравнению электродинамики магнитная сила F _m прямо пропорциональна изменению энергии магнитного поля E _m, что есть функция от силы тока в соленоиде I и индуктивности электромагнита L :

^F m = — gradE m = — grad

I 2 L

1 ² d L

2 d z

Индуктивность, в свою очередь, можно записать как:

L = N 2

R m где N2 – количество витков соленоида, Rm – маг- нитное сопротивление системы.

Учитывая, что I и N константы, получаем сле- дующее уравнение:

Fm =- ™ Т[T 1 .

2 dz ^ R m J

Магнитное сопротивление системы Rm, в свою очередь, зависит от следующих геометрических параметров (рисунок 1): толщина выступающей части магнитопровода b; величина зазора g между проводящей оболочкой сердечника и выступающей частью магнитопровода; толщина проводящей оболочки сердечника δ; положение сердечника в магнитопроводе, что описывается расстоянием от верхнего торца сердечника до выступающей части магнитопро- l

₁ и длиной выступающей части сердечника l ₂; внешний D ₂ и внутренний D ₁ диаметры сердечника.

По итогу тепл ового расче та, при условии, что в соленоиде будет течь то к I в 4 А, о птимальным количеством витков N является 56 0 при диаметре проволоки d 0.4 мм.

Для первичного анализа была построена параметрическая конечно-элементная модель (КЭМ) с целью итерационного расчета магнитной силы в программном обеспечении (ПО) ANSYS Maxwell с изменением одного из выше приведенных параметров при сохранении всех остальных.

Том 9

По результатам предварительных расчетов и выступающей частью магнитопровода, что, со-было установлено, что магнитная сила растет при ответственно, приводит к снижению магнитных увеличении значений приведенных параметров, показателей. Приняв во внимание увеличение

за исключением внутреннего диаметра сердечника D1 (рисунок 2), толщины токопроводящей оболочки δ (рисунок 3) и величины зазора g. Это объясняется тем, что увеличение внутреннего диаметра сердечника приводит к уменьшению площади поперечного сечения и, соответственно, насыщению материала. В свою очередь, увеличение значений параметров δ и g приводит к уменьшению плотности магнитного потока между сердечником массово-габаритных показателей и уменьшение магнитной характеристики, толщину токопроводящей оболочки и величину зазора можно полностью исключить из оптимизационной модели, а в расчетах использовать минимальные значения, равные 0.1 мм.

Таким образом, задача оптимизации сводится к оптимизации следующих параметров, приведённых в таблице 1.

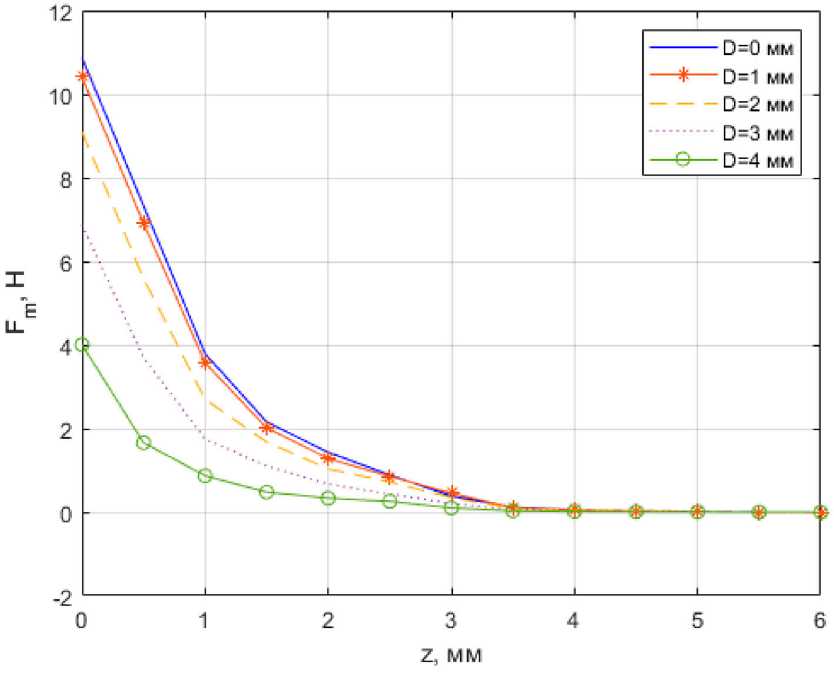
Рисунок 2. График зависимости магнитной силы от положения сердечника относительно начала координат при разном значении величины диаметра D ₁

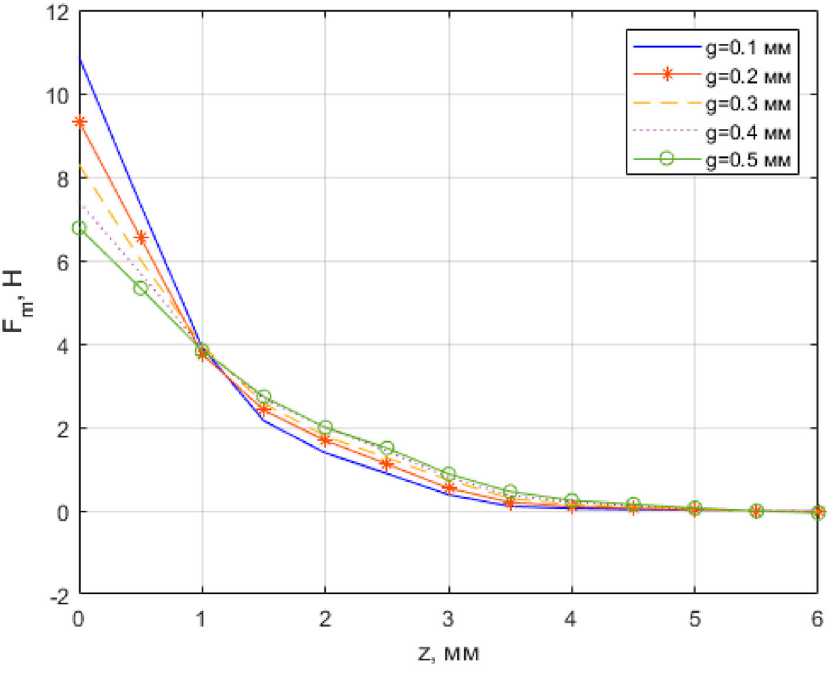
Рисунок 3. График зависимости магнитной силы от положения сердечника относительно начала координат при разном значении величины толщины токопроводящей оболочки сердечника δ

Таблица 1

Параметр	Значение параметра, мм
Толщина выступающей части магнитопровода b	3
Расстояние от верхнего торца сердечника до выступающей части магнитопровода l 1	0
Длина выступающей части сердечника l 2	8
Внутренний диаметр сердечника D 1	0
Внешний диаметр сердечника D 2	5,5

Основные конструктивные параметры

3.    Описание алгоритмов

• А. Алгоритм оптимизации

Для решения задачи оптимизации была применена теория игр, а именно игра Штакельберга [15] (рисунок 4). Суть данной игры состоит в том, что у нас имеется два типа игроков: лидер и последователь, которые выражаются соответствующими функциями fL и fF. Данные функции имеют набор пересекающихся параметров {xL, xF}. Особенность лидера состоит в том, что он, имея иерархическое преимущество, первый изменяет значения своих параметров xL, сохраняя неизменными значения параметров последователя xF, в целях поиска оптимального значения целевой переменной своей функции. После оптимизации лидера к оптимизации приступает последователь, который также ищет оптимальное значение целевой переменной своей функции через изменение значений своих параметров xF, сохраняя неизменными значения

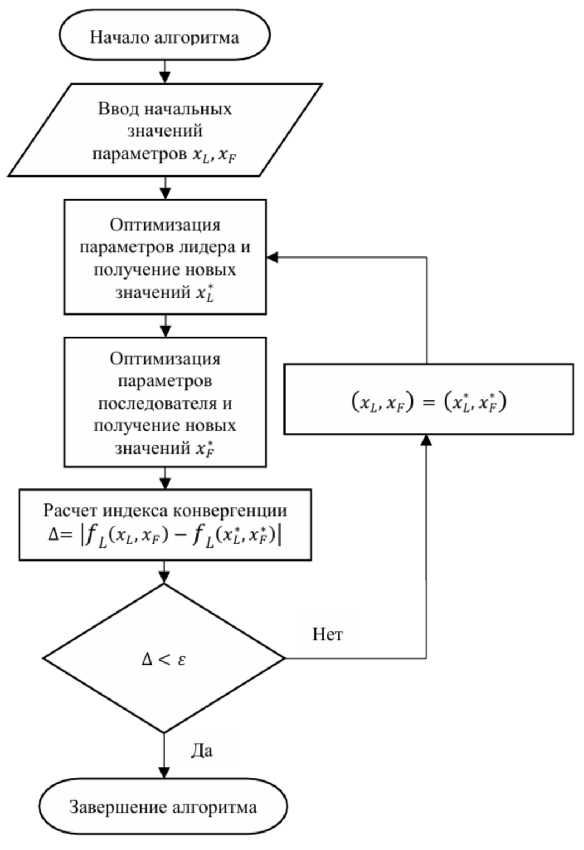
Рисунок 4. Алгоритм оптимизации модели

параметров лидера x _L. Далее цикл повторяется до момента, когда лидер больше не сможет оптимизировать свою целевую переменную, изменяя исключительно значения параметров x _L. Такое состояние называется равновесием Штакельберга.

Б. Алгоритм машинного обучения

Решение задачи оптимизации требует построения математической модели устройства, выражающей магнитную силу от определенных конструктивных параметров. Учитывая сложность выведения аналитической зависимости, восполь-

• ¹⁹⁴ зуемся алгоритмом машинного обучения.

Существует множество алгоритмов машинного обучения, применяемых для решения широкого спектра задач [16–20], поскольку данный случай состоит в получении сложной нелинейной зависи- мости от нескольких параметров, воспользуемся моделью, представляющей собой нейронную сеть.

Составленная нейронная сеть включает в себя три полносвязных скрытых слоя с гиперболическим тангенсом в качестве функции активации, для выходного слоя использовалась линейная функция активации (рисунок 5). Количество нейронов выбиралось кратно количеству признаков в следующем порядке: 12 нейронов для первого скрытого слоя, 24 – для второго, и 48 – для третьего.

Уравнение сети можно записать в следующем виде:

л

У = О ’4

( 48

Z w? )

Z ^2

к к = 1

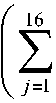
w kj

Z w⁽ 1) x + b ( °

Z jii j где y – предсказанное целевое значение, w(n) – веса n-го слоя, b(n) – параметр сдвига n-го слоя, σn –

Том 9

функция активации n -го слоя, x _i – входной параметр.

Для предотвращения переобучения модели использовалась Байесовская регуляризация. Данный метод показал лучшую точность относительно других методов [21], а также продемонстрировал свою эффективность при обучении нейронной сети на ограниченном наборе данных [22]. Суть данного метода состоит в минимизации функции потерь, которая записывается следующим образом:

F ( w ) = -1 Л. Р- Л2 + « ll w 11 2 ,

N где y – вектор истинных значений, y – вектор предсказанных значений, w – вектор весов, N – количество наблюдений в обучающей выборке, α и β – коэффициенты регуляризации.

Если α >>  β, то ве са модели уменьшаются и модель становится менее точной, при этом повышается ее вариативность, в противоположном случае, когда α << β, точность модели возрастает, но также растет риск переобучения. В процессе обучения алгоритм автоматически подбирает данные коэффициенты, стремясь получить достаточно высокую точность предсказания целевых значений с минимальными рисками переобучения.

Для обновления весов вместо стандартного градиентного спуска с обратным распространением использовался алгоритм Левенберга-Марквардта. Данный алгор итм быстрее градиентного спуска , поскольку включа ет в себя алгоритм Ньютона-Гаусса, а также хорошо подходит для ограниченного набора о буч ающей выбор ки [22]. Обно вле ние весов происходит по следующей формуле:

w+1 = w,-( JTJ + m )-1 JTe, где J – матрица Якоби, которая состоит из первых производных ошибок нейронной сети по весам, е –

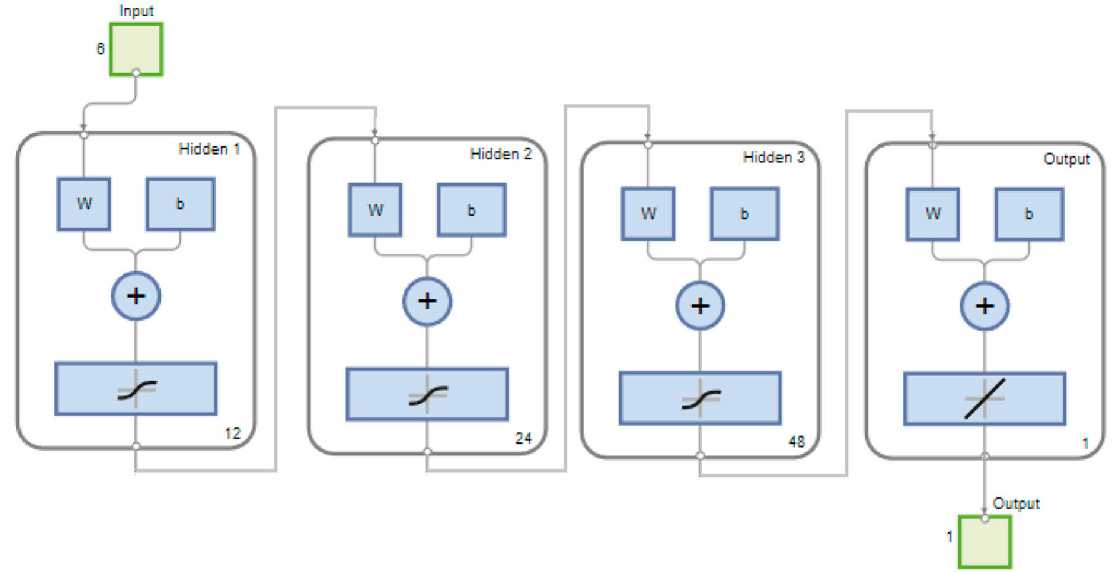
Рисунок 5. Общий вид нейронной сети

П. Н. Максимов, Ф. К. Синьковский, В. Н. Максимов ,, вектор ошибки, μ – коэффициент демпфирования Левенберга, I – единичная матрица.

Если после обновления весов возросла ошибка, то алгоритм увеличивает коэффициент демпфирования μ, что делает алгоритм более «градиентным», это приводит к уменьшению шага обновления и, соответственно, росту времени обучения. Если же после обновления весов ошибка стала меньше, то алгоритм уменьшает коэффициент демпфирования μ, вследствие чего алгоритм ведет себя больше как м ет од Ньютона-Гаусса, что ускоряет время обучения.

Поскольку нейронные сети чувствительны к масштабу данных, предварительно перед обучением проводилась нормализация, суть которой представлена следующим выражением:

• x. - x -

• i min xni =               ,

x - x -max min где xni – i-е значение параметра в выборке после нормализации, xi – i-е значение параметра в вы- борке, xmin – минимальное значение параметра в выборке, xmax – максимальное значение параметра в выборке.

Для оценки результатов обучения в качестве метрики выбран коэ ффициент детерминации R ², представленный следующим уравнением:

R ²

n

E ( yi ^- y ) 2

= 1

n ,

E ( y ^- y ) 2

= 1

где y _i – i -е значение целевой переменной, y ˆ _i – предсказанное i -е зн а чение целевой переменной, y – среднее значение целевой переменной по выборке, n – количество целевых переменных в выборке.

Для обучения модели в ПО MATLAB был составлен алгоритм обучения, представленный на рисунке 6. Генерация выборки, необходимой для обучения и валидации модели, осуществлялась через параметрическую КЭМ, а в целях ав-

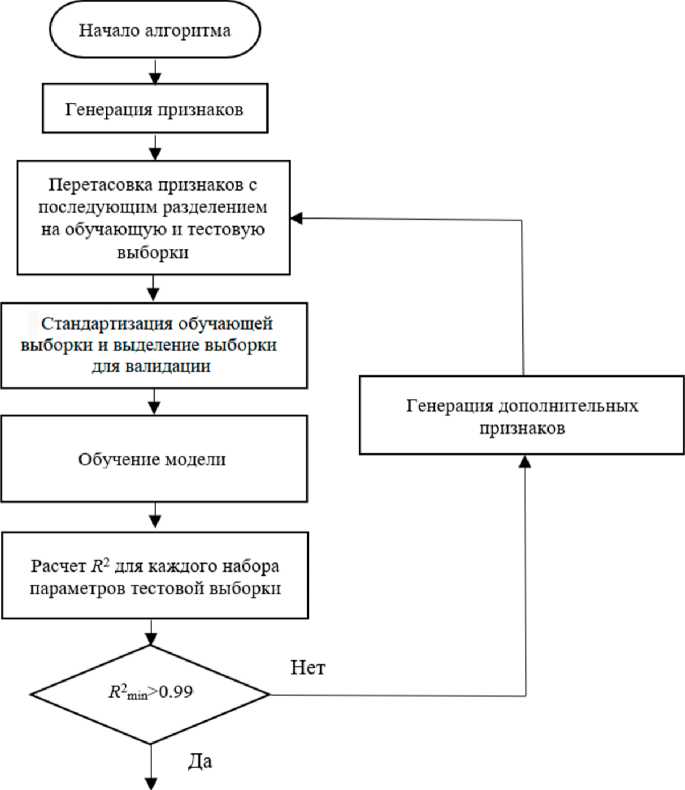
Завершение алгоритма

Рисунок 6. Алгоритм обучения нейронной сети

томатизации расчетов был написан соответствующий скрипт, сопряженный с MATLAB.

4. Оптимизация параметров

Том 9

где F _c – сила сопротивления срабатыванию; F _m0 – магнитная сила в начальный момент времени.

Т аки м обра зом, о птимизационная модель имеет следующий вид:

Учитывая, что наш случай оптимизации состоит в достижении надежности срабатывания, при минимальной массе устро йства с удовлетворением требований прочнос т и, в качестве лидера f _L выбрано отношение минимального значения магнитной силы н а рабоче м участке движения сердечника F _m(min) к массе изделия M , а в качестве ¹⁹⁶ последователя f _F коэффици е нт запаса прочности сердечника η.

F m (min) ^fL                ; ^f F ^[l ^.

M

Стратегия игроков состоит в том, что лидер стремится максимизировать свою целевую переменную, в то время как последователь, в целях избежания избытка прочности и обеспечения надёжности, минимиз ироват ь с выполнением условия, что η ≥ 3, n ₁ ≥ 3, n ₂ ≥ 2. Коэффициенты n ₁ и n ₂ представляют собой следующее:

F         F m (min)

n 1 = -m ⁰ ; n 2 = ——, FF

F max M 2 (DvD2,li,12,b,z),mmn(Di,D2,12);

П >  3, n 1 >  3, n 2 >  2;

D 1 ,D 2 ,1 1 ,1 2 ,b e R

Для вывода зависимости магнитной характеристики F _m от параметров 1 1 , 1 2 , D 1 , D 2 , b , z была простроена регрессионная модель согласно алгоритму, приведенному на рисунке 6. Генерация значений параметров происходила в пределах, указанных в таблице 2.

В первой итерации генерировалось 50 комбинаций значений параметров, к которым в последующих итерациях прибавлялось по 50 комбинаций.

В ходе расчета было просчитано 5 итераций и сгенерировано в общем 250 комбинаций значений параметров. На рисунке 7 приведено минимальное значение коэффициента детерминации R ²_min для отдельного набора параметров тестовой выборки в каждой итерации.

Таблица 2

Параметр	l 1 , мм	l 2 , мм	D 1, мм	D 2, мм	b , мм
Нижняя граница	0	5	0	4	1
Верхняя граница	6	12	11	12	6

Диапазон генерируемых значений параметров

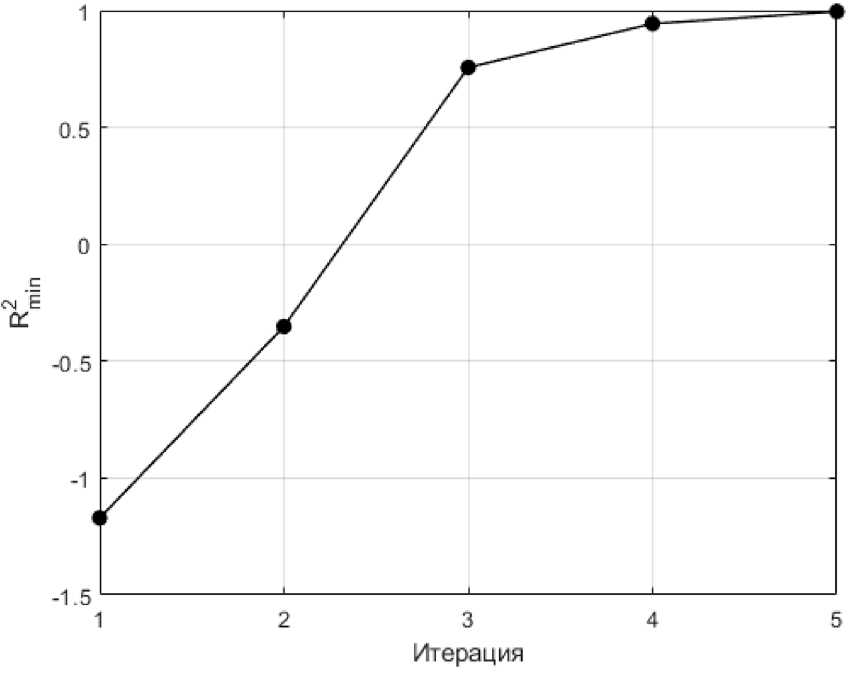
Рисунок 7. Минимальное значение коэффициента детерминации для отдельного набора параметров тестовой выборки в каждой итерации

Для проверки точности модели было дополнительно сгенерировано 50 комбинаций параметров и проведен расчет коэффициента детерминации, результаты продемонстрированы на рисунке 8. По результатам расчета минимальное значение коэффициента R ²_min составило не менее 0.90, что говорит о получении модели высокой точности.

После получения полиномиальной регрессии была проведена оптимизация по алгоритму, приведенному на рисунке 5. Оптимизируемые параметры были поделены на следующие группы x _L { l ₁, D ₂, b }, x _F { l ₂, D ₁}. Оптимизация проводилась в диапазоне значений согласно таблице 3.

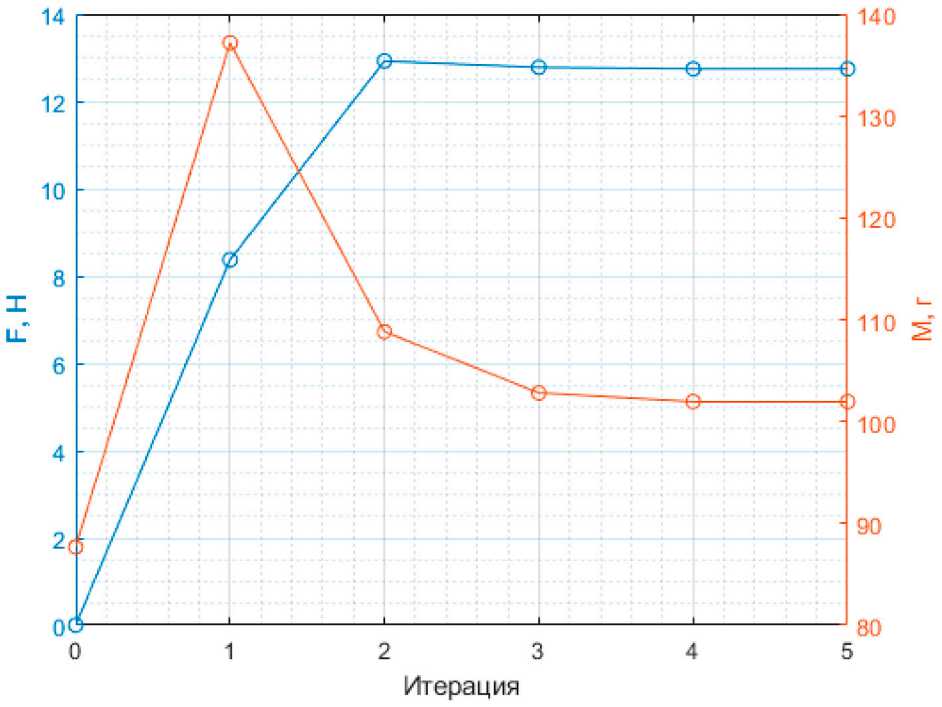
Для оптимизации параметров потребовалось 5 итераций. Оптимизированные параметры приведены в таблице 4. На рисунках 9 и 10 представлены результаты оптимизации.

С оглас но таб лиц е 4 оп тимиз ация позволила значительно увеличить минимальную магнитную силу на рабочем участке при увеличении массы в . ра за.

5. Построение математической модели устройства

Снова запишем уравнение движения подвижного элемента устройства:

m a = F m - F b - F f - F_s .

Расписав члены уравнения, получим следующую функцию

m a =

1 ² N ² d ( 1 ^

2   d z

R

^- ! V ° (^vx B ) dV ^- k s xx

⁺ k f R ,

Диапазон оптимизируемых значений парам етров

Таблица 3

Параметр	l 1, мм	l 2 , мм	D 1, мм	D 2 , мм	b , мм
Нижняя граница	0	5	0	4	1
Верхняя граница	6	12	11	12	6

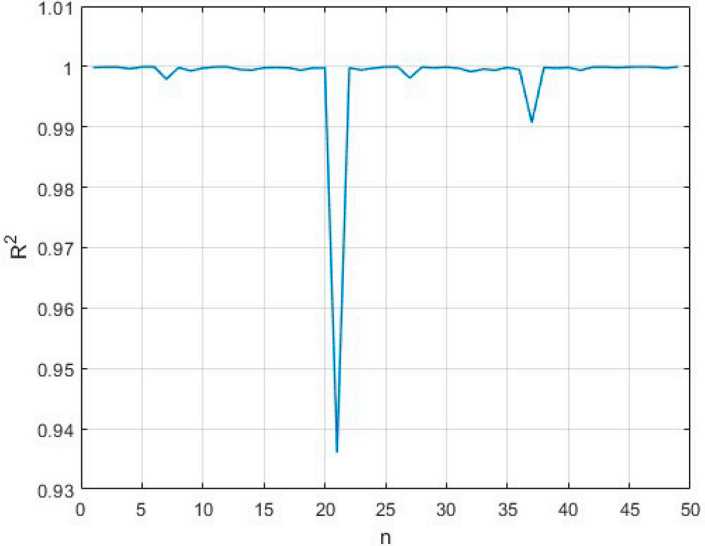
Рисунок 8. Значения коэффициента детерминации для каждой комбинации значений параметров дополнительных данных

Результаты оптимизации

Таблица 4

Переменные	l 1, мм	l 2, мм	D 1, мм	D 2, мм	b , мм	F m(min) , Н	М , г
Начальные значения	0	8	0	5,5	3	0,0056	87.7
Оптимизированные	4	10	4.6	9.8	1.3	12,745	101.9

If ОСМИЧЕСКИЕ АППАРАТЫ И

ТЕХНОЛОГА иен

Том 9

где v – вектор скорости подвижного элемента, В – вектор магнитной индукции, k _s – коэффициент упругости пружины, x * - изменение длины пружины, k _f - коэффициент трения, R - реакция опор в системе под награждением.

Учитывая сложное, нелинейное поведение первых двух компонент правой части уравнения, для их расчёта воспользуемся КЭМ и методами прикладной математики.

Проведя соответствующие расчеты, запишем уравнение движения в полном виде:

x =

2226  6                         12  5  15

N-I- ^\ 5 j -- N²1 ² Х£Ь ^-^k 5 ⁵ - ²

²      i = 1 j = 1                                 i = 1 j = 5 k = 1

. 15 - i

-

*

^ 1 )-kfR -, ' m

где Z ij и Y ijk - расчетные коэффициенты, x ₀ * - изменение длины пружины в начальный момент времени, P – нагрузка н а серд ечник.

2          3

Итерация

12 -

10 -

110 ^

Рисунок 9. Значение массы и минимальной втягивающей силы на каждой итерации оптимизации

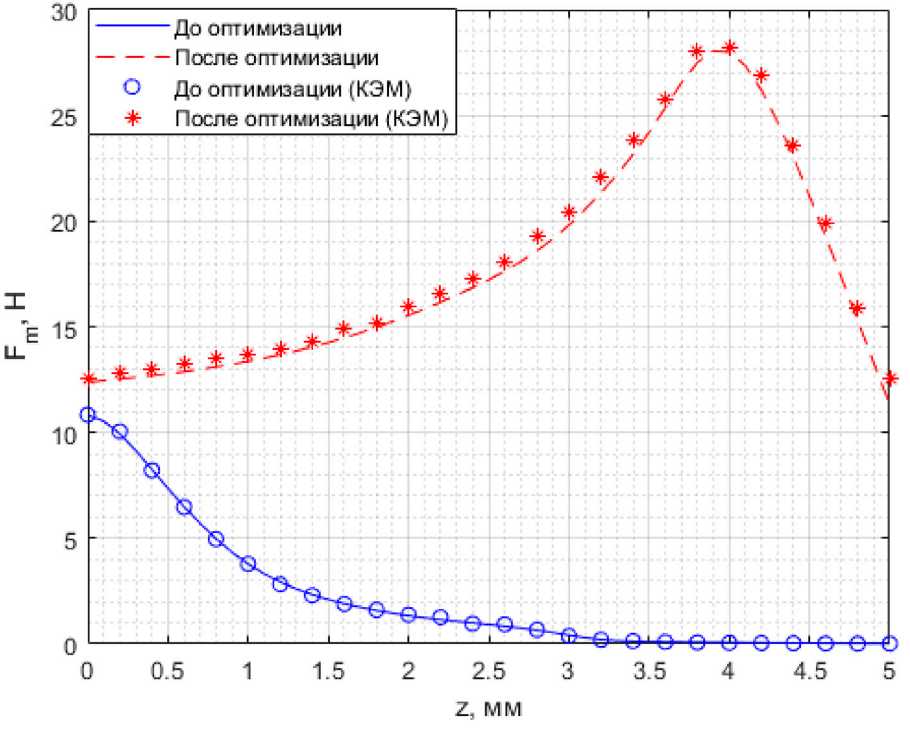
Рисунок 10. Сравнение магнитной силы F _m до и после оптимизации для КЭМ и полученной модели

Математическое моделирование и оптимизация магнитной характеристики инициирующего устройства…

Для простоты запи си за меним члены уравнения:

• ■

x =

— N ²1² f 2 — k s X ‘

I ²

—

Л

k f R -.

m

Теперь зададим начальные условия:

x 0 = 0; x o = ⁰.

Также, исходя из условия, что нагрузка действует только первые 5 мм хода, запишем условие для силы трения:

x >  0.005---- > R = 0 .

Для решения полученного уравнения воспользуется ПО MATLAB Simulink, на рисунке 11 представлена блок-схема устройства.

Приняв k _s = 340, k _f = 0.01, x ₀^* = 0.003 мм, была приведена симуляция при разных значениях толщины токопроводящей оболочки сердечни-

δ с учетом индуцированных токов и без них. Результаты симуляции приведены на рисунке 12.

При рассмотрении результатов симуляции становится видно, что наличие токопроводящ е й оболочки с индуцированными токами способствует значительному снижению ударной нагрузки при незначительном увеличении времени срабатывания.

Проделанные расчеты демонстрируют возможность разработки электромагнитного инициирующего устройства с высокой скоростью срабатывания и низким ударным воздействием.

Заключение

В данной работе были определены основные геометрические параметры магнитного инициирующего устройства с низким ударным воздействием, а также была построена математическая модель данного устройства с применением МКЭ

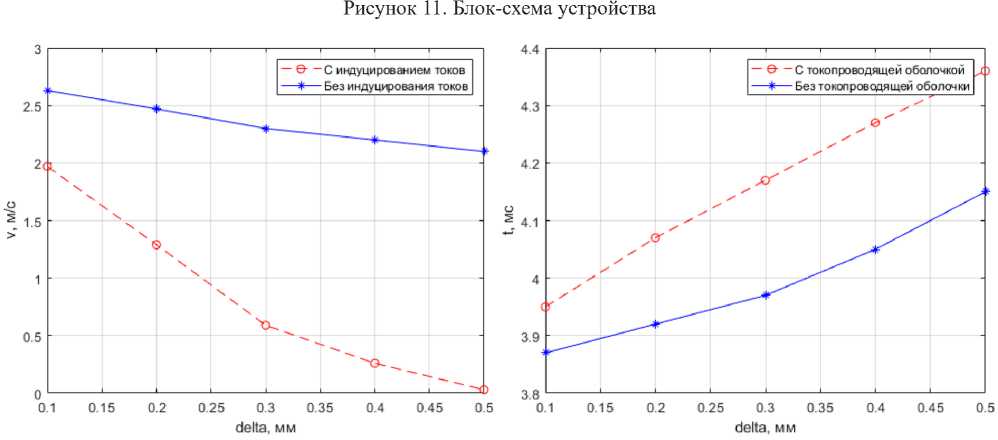
Рисунок 12. Скорость сердечника в конечном положении и время срабатывания зависимости от толщины токопроводящей оболочки сердечника

и алгоритма машинного обучения. Данная модель выражает магнитную силу F _m от основных конструктивных параметров, что позволило провести оптимизацию, минуя вывод аналитической формулы данной характеристики. В качестве алгоритма оптимизации применялся алгоритм, реализующий игру Штакельберга из теории игр. Данный алгоритм подходит для выполнения многоцелевой оптимизации, и его эффективность подтверждается результатами оптимизации, где оптимизирован-

Том 9

ные значения параметров позволили значительно увеличить магнитную силу при увеличении массы в 1.16 раза.

Затем было составлено уравнение движения устройства и проведена симуляция, которая показала высокую скорость срабатывания устройства (до 4.5 мс) и низкое ударное воздействие. Данные результаты позволяют перейти к следующему этапу проработки изделия с последующим изготовлением опытного образца.