Математическое моделирование и оптимизация структуры течения в ступени радиально-осевой турбины микрогазотурбинной установки

Одним из перспективных направлений развития малой энергетики является разработка и внедрение в народное хозяйство микрогазотурбинных установок (МГТУ) как автономных энергетических агрегатов малой мощности. Привлекательность МГТУ как источника электроэнергии обусловлена высокой надежностью, значительным ресурсом, в 2-3 раза превышающим ресурс дизельных и газопоршневых агрегатов, простотой эксплуатации и обслуживания, высокой экологичностью [1].

Основу МГТУ составляет газотурбинный двигатель, приводящий в действие электрический генератор. Строгой границы между газотурбинной и микрогазотурбинной установками нет, однако принято считать, что в МГТУ должен быть рекуператор теплоты выхлопных газов, благодаря которому повышается ее общий к.п.д. Кроме того, конструкция МГТУ предусматривает одну ступень компрессора и одну ступень турбины, имеющие высокую частоту вращения (> 60 000 об/мин).

В МГТУ, как правило, применяется газовая турбина радиально-осевого типа по следующим причинам:

• 1)    при относительно небольших мощностях к.п.д. радиально-осевых турбин больше, чем у осевых;

• 2)    в ступени турбины можно осуществить несколько бóльший теплоперепад, так как при одинаковых напряжениях в рабочем колесе окружные скорости в радиально-осевых турбинах могут быть большими, чем в осевых;

• 3)    рабочие колеса турбины проще в изготовлении и надежнее благодаря малому числу лопаток и простой конфигурации.

Параметры турбины должны определяться исходя из ряда требований: высокого к.п.д., необходимой прочности, технологичности и простоты конструкции. В этих требованиях, часто противоречивых, получение высокого к.п.д. ступени представляется одной из главных задач.

Объектом исследований, рассматриваемым в настоящей статье, является радиально-осевая турбина МГТУ-100 (МГТУ, имеющая электрическую мощность 100 кВт). Так как оптимальное значение степени повышения полного давления в компрессоре МГТУ обычно находится в диапазоне 4,5…5,5 [2, 3], степень понижения полного давления в турбине с учетом гидравлических потерь в камере сгорания, рекуператоре и выхлопном устройстве составляет п _т >  3,5^4. Столь высокая величина теплоперепада традиционно срабатывалась в двухступенчатых турбинах, однако с целью упрощения конструкции, улучшения ремонтопригодности и снижения стоимости требуется спроектировать высокоэффективную одноступенчатую радиально-осевую турбину. В случае МГТУ-100 степень понижения полного давления в турбине п т = 4,1.

На первом этапе проектирования выполнен газодинамический расчет турбины по средним параметрам по методике, приведенной в работе [4]. При этом контролировалось выполнение следующих условий:

• 1.    Окружная скорость на входе в рабочее колесо не должна превышать допустимую u доп ≈ 515 м/с. Для принятой частоты вращения вала n = 65 000 об/мин соответствующий диаметр на входе в колесо d 1 = 150 мм.

• 2.    Приведенная скорость газового потока на выходе из соплового аппарата λ ≤ 1. Данное условие приводит к необходимости задаваться достаточно высокой степенью реактивности турбины (степени использования тепловой энергии газа в колесе турбины): ρ ≈ 0,53, что лежит за пределами диапазона оптимальных значений р_опт е 0,15..0,5 [4].

• 3.    Соблюдение геометрических ограничений, связанных с технологичностью изготовления ступени турбины.

В результате расчета определены основные размеры турбины (высоты лопаток и диаметры, на которых они расположены), в которые в соответствии с методикой, приведенной в работе [5], вписаны периферийный и втулочный меридиональные обводы (рис. 1, б).

а)

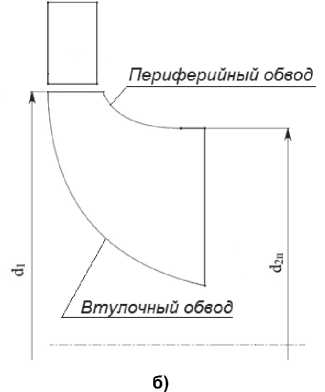
Рис. 1. Радиально-осевая турбина: а – трехмерное представление; б – меридиональное сечение; d 1 – диаметр на входе в рабочее колесо; d 2п – диаметр периферийного обвода на выходе из рабочего колеса

Профиль лопатки рабочего колеса построен путем его изгиба по дуге параболы. Профиль лопатки соплового аппарата задан параметрической моделью (рис. 2). Контуры спинки и корытца сопловой лопатки образованы кривой Безье и прямолинейным выходным участком каждый, входная и выходная кромки заданы дугами окружностей.

На следующем этапе проектирования выполнены анализ и оптимизация течения в сопловой решетке с использованием методов вычислительной гидродинамики (CFD). Для этой цели в программном комплексе ANSYS CFX подготовлена трехмерная параметрическая расчетная модель течения в одном межлопаточном канале решетки (с учетом галтели в области втулочного обвода) с учетом информации об опыте трехмерного численного моделирования турбомашин и рекомендаций, приведенных в работах [6–20].

Варьируемыми параметрами лопатки являлись:

• 1.    Геометрические параметры l удл , δ, γ – как в наибольшей степени влияющие на форму профиля. Длины прямолинейных участков спинки и корытца приняты равными l _сп = 0,45· l ; l _кор = 0,35· l , размеры кромок d вх = 5 мм, d вых = 1 мм.

• 2.    Количество лопаток n са = 22; 23; 24.

  

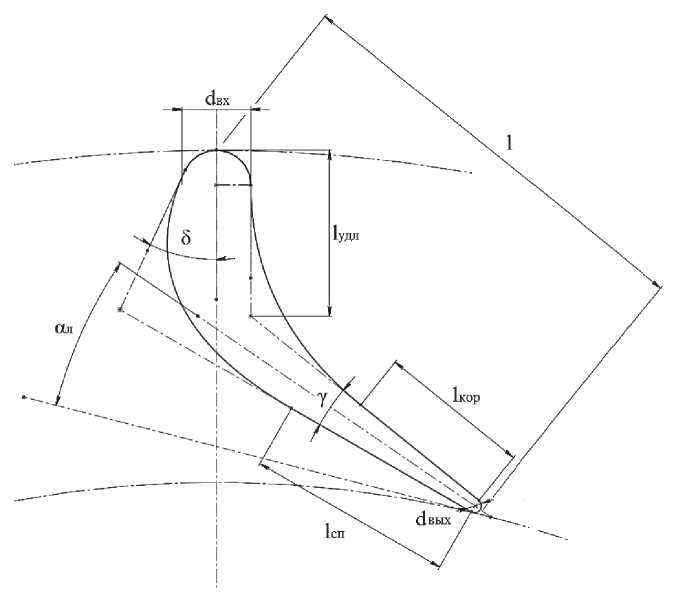
  Рис. 2. Параметризация профиля сопловой лопатки: l – хорда профиля; d вх – диаметр входной кромки лопатки; d вых – диаметр выходной кромки лопатки; l удл – радиальное удлинение лопатки; δ – угол отгиба лопатки; α л – лопаточный угол на выходе из соплового аппарата; γ – угол расклинки лопатки; l кор – длина прямолинейного участка корытца; l сп – длина прямолинейного участка спинки

  
  

Оптимальные форма и количество лопаток находились для каждого значения угла α л = 12; 15; 20; 25° (существует технологическое ограничение на изготовление лопатки с α_л< 12°).

При этом угол потока на выходе из соплового аппарата α1 в первом приближении рассчитывался по формуле [4]:

а 1 = arcsin

a

I tq ( ^ ci ) J

где а – ширина узкого сечения; t – шаг; q – газодинамическая функция расхода; с 1 – скорость потока в абсолютном движении на выходе из соплового аппарата;

Действительное значение угла α 1 устанавливалось по результатам расчета в ANSYS CFX.

С использованием модуля ANSYS TurboGrid построена расчетная сетка (рис. 3), качество которой контролировалось относительно стандартных критериев, реализованных в модуле. Количество расчетных ячеек при этом составило ≈ 550 000.

Рассматривалась стационарная задача, в качестве модели турбулентности выбрана SST-Ментера. Задавалась следующая комбинация граничных условий: полная температура T0* и рас- ход газа Gг на входе в расчетную область – статическое давление p1 на выходе из нее. Статическое давление p1 предварительно определялось в газодинамическом расчете турбины по средним параметрам для каждого значения угла потока α1. Требуемый перепад давлений *

p в сопловом аппарате     обеспечивался p1

за счет изменения высоты лопатки в расчетной модели.

В качестве критерия оптимизации принят коэффициент скорости φ – вели- чина, учитывающая потери в сопловом аппарате. Кроме того, оценивалось значение коэффициента восстановления полного давления в расчетной области σ:

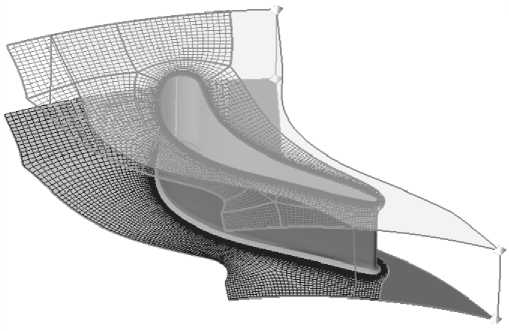
Рис. 3. Расчетная сетка в межлопаточном канале соплового аппарата

* p 0 ^v * , p ₁

Ф = ^,                                                                       (3)

c1t где p0* – полное давление на входе в сопловой аппарат; p1* – полное давление на выходе из соплового аппарата; с1 – действительная скорость на выходе из соплового аппарата; с1t – теоретиче- ская скорость на выходе из соплового аппарата.

На рис. 4 приведен вид оптимизированной сопловой решетки с лопаточным углом α л = 12 и количеством лопаток n са = 23.

На рис. 5 и 6 показаны результаты расчета данной оптимизированной сопловой решетки.

Как следует из рис. 5, в межлопаточном канале отсутствуют пространственные завихрения и неравномерности

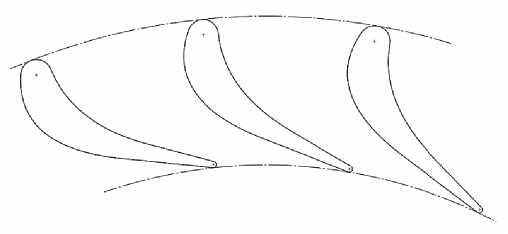
Рис. 4. Оптимизированная сопловая решетка

течения.

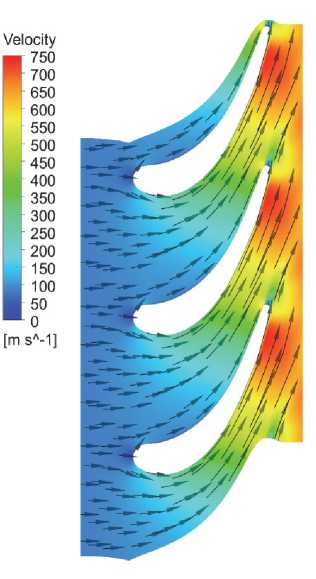
На рис. 6 приведены результаты расчета в виде полей скорости и давления на средней линии сопловой решетки, из которых следует отсутствие выраженных отрывных зон на спинке и корытце лопатки.

Далее выполнено параметрическое исследование течения в ступени радиально-осевой турбины. Варьируемыми параметрами являлись лопаточный угол α 1л соплового аппарата (путем подстановки в расчетную модель соответствующей оп т имизированной сопловой лопатки) и диаметр периферийного обвода d 2п на выходе из рабочего колеса. Радиальный зазор в рабочем колесе при этом оставался постоянным δ рз = 0,8 мм.

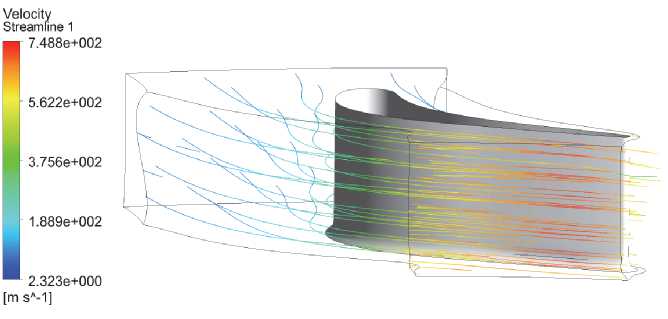
Рис. 5. Пространственное течение в сопловом аппарате

р

■ 460000 ■ 440000

- 420000

- 400000

- 380000

- 360000

- 340000

- 320000

- 300000

- 280000

- 260000

- 240000

- 220000 ■200000 I - 180000 ■ 160000

[Ра]

Рис. 6. Поле скорости и давления в сопловом аппарате

В данном случае при построении расчетной модели необходимо вы п олнить ус л овие приблизительного равенства площадей на выходе из ст а торной части расчетн о й области и на входе в роторную часть расчетной области. Для этого в расчетную модель включены 3 межлопаточных канала соплового аппарата и 2 межлопаточных канала рабочего колеса (рис. 7). Об-

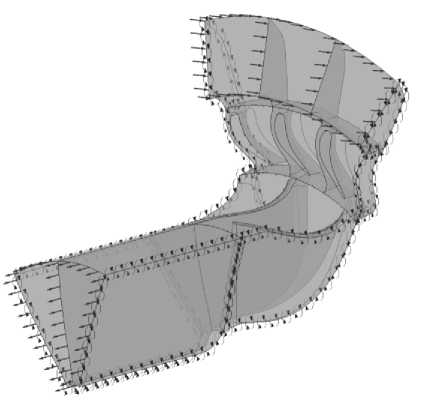
Рис. 7. Расчетная модель ступени турбины

щее количество ячеек расче т ной сетки составило ≈ 2 500 000.

В к ачестве граничных у с ловий также задавалась ко м бинация: полная температура T ₀ ^* и расход газа G г на входе в сопловой аппарат – статическое давление p 2 на выходе из рабочего колеса. Критерием оптимизации являлся коэффициент полезного действия турбины η.

На р ис. 8 представлены р е зультаты расчета варианта с α_л = 12 и d _2п = 116 мм в виде поля скорости на сред н ей линии ступени тур б ины.

Из рис. 8 видно, что на спинке рабочей лопатки за входной кромкой имеет место отрыв потока. Как следует из расчетов, отрыва потока не удается избежать даже при использовании сопловой решетки с αл = 25° (α1 ≈ 28°). В качестве решения проблемы может быть предложено специальное профилирова- ние рабочей лопатки, однако оно требует дополнительного исследования.

Результаты оптимизационных расчетов представлены на рис. 9 в виде графической зависимости к.п.д. ступени турбины от α л и d 2п , где указанн ы е значения параметр о в соответс т вуют рассматриваемому диапазону. Максимальный к.п.д. ступени турбины η достигается в т.А.: α_л = 12° и d 2п = 116 мм (рис. 9).

Таким образом, математическое моделирование течения с использова н ием ANSYS CFX позволяет найти оптимальную геометрическую конфигурацию ступени радиально-осевой турбины в рамках существующих технологических огран и чений. На следующем этапе исследования

Velocity

| 6.979е+002

6.284e+002

5.590e+002

U 4.8956+002

4.2006+002

3.5066+002

2.8116+002

2.1166+002

1.4216+002

7.2676+001

3.2006+000

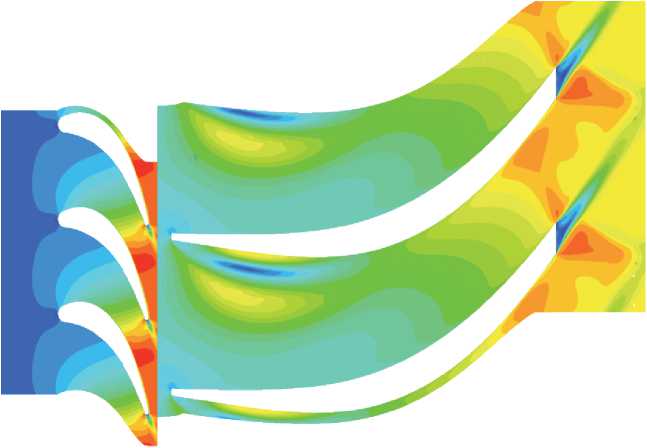
Рис. 8. Скорость потока на средней линии ступени турбины

[m sA-1]

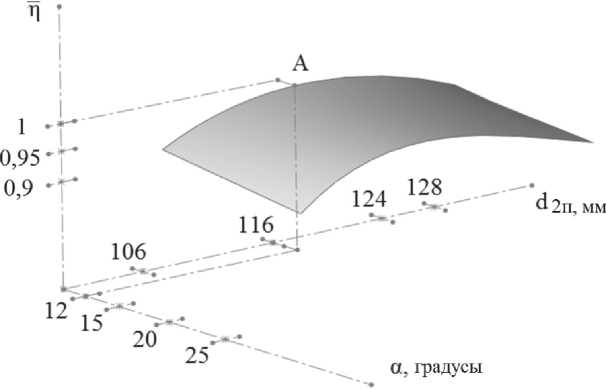
Рис. 9. Зависимость относительного к.п.д ступени турбины от α л и d 2п

будет выполнена верификация полученных результатов на испытательном стенде, которая позволит судить о правильности построения расчетной модели и алгоритма оптимизации.

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках комплексного проекта «Создание производства модельного ряда микротурбинных энергоустановок нового поколения» по договору № 02.G25.31.0078 от 23.05.2013 г. между Министерством образования и науки Российской Федерации и Открытым акционерным обществом «Специальное конструкторское бюро «Турбина» в кооперации с головным исполнителем НИОКТР – Федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет).