Математическое моделирование и программирование на ЭВМ экономических задач

Во многих областях деятельности человека часто возникают задачи, которые требуют описать реальные природные объекты и процессы, с целью изучить их свойства, структуру и законы развития, а так же их внутренние и внешние связи. С одной стороны, это необходимо знать для результативного и эффективного управления объектом или процессом, а другой стороны для наиболее точного и надежного прогнозирования.

Моделирование - это описание реальных объектов и процессов, а полученная абстракция - модель. Модели квалифицируются по способу их описания. Например, математические модели (используя математический аппарат, происходит описание модели), информационные модели (происходит описание информационных процессов), вербальные модели (используя тест, происходит описание модели).

Перенесение математической модели в среду ЭВМ и переход от аналитических методов к численным методам - является главной особенностью компьютерного математического моделирования. На практике это означает замену всех бесконечно малых и бесконечно больших величин некоторыми конечными величинами, дискретизация функций и непрерывных переменных. Такое представление позволяет описать и перенести любые математические модели в среду готовой компьютерной программы для дальнейшей работы с ней.

Любая модель проходит несколько этапов составления.

Первый этап - постановка задачи. Здесь определяется объект модели, начальные условия и что должно получиться в результате.

Второй этап - формализация. Здесь уясняются существенные свойства объекта и их взаимосвязь.

Третий этап - поиск математического описания модели. Это самый ответственный момент в моделировании. Поскольку выбор неправильного математического описания для любой связи, части, переменной модели может привести к полной или частичной неработоспособности модели в целом. Для описания взаимодействий выбираются уже известные функциональные зависимости, то есть исследованные ранее, или статистическую зависимость, то есть табличные описания.

Четвертый этап – программирование. Выбирается конкретная среда работы, или среда языка программирования, или среда существующего приложения, или все вместе. В виде программы или пользовательского документа создается, собственно, модель. Проводятся тестирования модели главной целью, которой является выяснения работоспособности и степени адекватности полученной модели. Затем создаются инструменты работы с моделью.

Рассмотрим пример математического моделирования экономической задачи. Цель нашего моделирования - это изучение процесса роста выпуска продукции, его графическое представление и определение прогнозных значений в некоторый момент времени.

Первый этап. Создать в среде MS Excel таблицу и диаграмму, которая определит уровень выпуска продукции в определенный момент времени и позволит нам увидеть график его изменения во времени.

Второй этап. Узнать цену продукции, количество продукции, реализованной на момент времени t, инвестиции в производство.

Трети этап. Предположим, что цена продукции Р фиксированная. Обозначим через Q(t) количество продукции, реализованной на момент времени t. Тогда PQ(t)- доход на этот момент времени. /(t) = mPQ(t) -инвестиции в производство, 0 <  т < 1. Если исходить из предположения о ненасыщаемости рынка или о полной реализации производимой продукции, то в результате расширения производства будет получен прирост дохода, часть которого опять будет использована для расширения выпуска продукции. Это приведет к росту скорости выпуска, причем скорость выпуска пропорциональна увеличению инвестиций, то есть Q’ = I/, где 1 - норма акселерации. Если обозначить к = 1тР, k=lmP, то Q’ = kQ(t). Общим решение этого дифференциального уравнения будет уравнение Q = Ce^kt , учитывая начальные параметры, получим Q = Q₀e^k(t-to). Это и есть искомая математическая модель.

Для проведения тестирования модели возьмем Q₀ = 100 единиц товара в момент времени t = 1 месяц, и к = 0,1. Шаг - 1 месяц. Тогда, полученная в MS Excel таблица выглядит следующим образом:

А п олученная диаграмма имеет вид:

Рост выпуска продукции

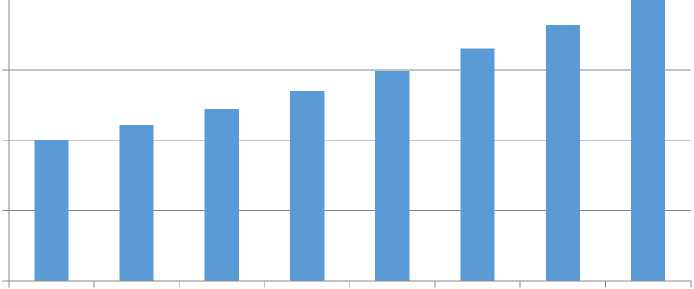
В заключение рассмотренного нами примера, отметим, что полученная модель приближенно описывает рост выпуска продукции при условии отсутствия конкуренции и пригодна для прогнозирования результата. Изменив допущение в экономическом состоянии рынка, мы получим другую модель исследуемого процесса, которая будет описывать рост выпуска продукции в условиях конкуренции.