Математическое моделирование и расчет конструктивных параметров измельчителей с переменным шагом винтовой линии шнека

Энергоемкость измельчительных механизмов, волчков, мясорубок или экструдеров определяется рядом сложных механических процессов, сопровождающихся деформацией и разрушением обрабатываемых материалов, а также затратами, обусловленными транспортировкой этих материалов в технологическую зону или зону резания. Конструктивные параметры элементов и узлов измельчительных механизмов являются определяющими в рассматриваемых процессах, поэтому их обоснование аналитическими методами является актуальной задачей. В частности, для обеспечения необходимого уровня давления в зоне резания или экструзии, а также с целью наискорейшего исключения пустот внутри массива продукта при подаче кускового измельчаемого материала винтовой шнек волчка или мясорубки выполняется с шагом, уменьшающимся от загрузочной воронки в направлении к режущей головке. При этом для случая постоянного шага винта шнека задача определения длины винтовой линии решается достаточно просто методами дифференциальной геометрии. Определение закона распределения давления по длине винтовой линии поверхности шнека даже постоянного шага представляет собой весьма сложную математическую задачу, определяемую в том числе и реологическими свойствами обрабатываемого продукта. В одних случаях этот закон выбирается линейным, в других принимается экспоненциальным, иногда считается степенным или более сложным, комбинированным, но корректный подход к решению этой проблемы может быть осуществлен, по-видимому, лишь на экспериментальной основе. В данной работе рассматривается вопрос аналитического определения длины винтовой линии шнека переменного шага и влияния закона изменения этого шага на конструктивные параметры волчка – измельчителя. Только после решения этой задачи можно переходить к подбору априори неизвестного закона распределения давления по его оси. Необходимо заметить, что в таком случае длина шнека волчка будет зависеть от закона изменения переменного шага винтовой линии и влиять на энергоемкость технологического процесса.

Очевидно, что в данном случае к основным определяемым параметрам в первую очередь относятся: начальный и конечный углы наклона винтовой линии шнека, закон изменения шага винта, длина винтовой линии, длина шнека.

Материалы и методы

Шнеки волчков, экструдеров и транспортирующих органов другого пищевого и иного оборудования непищевого назначения выполняются чаще всего в виде винтовой поверхности с переменным шагом [1], уменьшающимся в направлении перемещения продукта [2]. При этом продольный размер самого шнека и его корпуса также изменяется. Длина винтовой линии шнека и площадь винтовой поверхности, по которой осуществляется транспортировка продукта, оказывают существенное влияние на энергоемкость процесса, так как при реальных давлениях экструзии от единиц до сотен атмосфер [3] коэффициент трения скольжения сырья достигает больших значений, изменяясь от 0,02 до 0,7 [4; 5]. Таким образом, корректное вычисление длины винтовой линии шнека с переменным шагом, а также линейного размера корпуса волчка (горловины) является задачей актуальной. Действительно, по данным работы [6], около 35 % общих затрат энергии в волчках, мясорубках и экструдерах приходится на долю работы сил трения продукта о детали исполнительных механизмов при его перемещении по винтовой и цилиндрической поверхностям. Более того, известное [7] явление "шлюзования" продукта (его обратное перетекание в зазор между корпусом шнека и волчка) может быть математически корректно описано лишь при возможности расчета и точной оценки длины винтовой линии.

В случае постоянного шага винтовой линии шнека задача определения длины винтовой линии решается достаточно просто методами дифференциальной геометрии. Однако существенно сложнее оказывается математическое моделирование винтовой линии или поверхности шнека с переменным шагом.

Результаты и обсуждение

Для математического описания уравнения винтовой линии переменного шага и определения длины рассмотрим схему ее развертки, приведенную на рисунке.

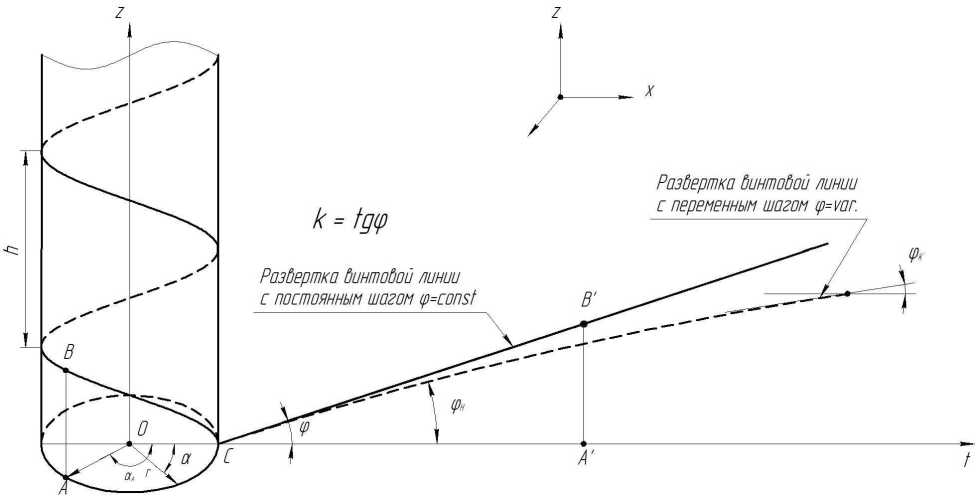
Рис. Схема развертки винтовой линии на плоскость Fig. The scheme of the helix scan on a plane

Участок СВ винтовой линии развернут на плоскость чертежа в виде отрезка прямой СВ'. Изображение перемещения точки А в положение В разворачивается в отрезок А'В'. Таким образом, для цилиндра радиуса r его поверхность САВ разворачивается в треугольник СА'В' с углом φ подъема винтовой линии у основания при повороте радиуса r на угол α _А .

Развертка окружности основания образующего цилиндра вдоль оси Сt выполнена в соответствии с соотношением t = rα,

где r – радиус окружности основания образующего цилиндра, α – угол поворота радиуса-вектора образующей окружности, t – длина дуги образующей окружности.

Угол подъема винтовой линии шнека φ определяется отношением шага винтовой линии h к длине развернутой окружности основания образующего цилиндра:

^tg ф = h^- .                                           (2)

2 n r

Далее обозначим к = tg^.

Как известно [8], параметрическое уравнение винтовой линии имеет вид трех функциональных зависимостей соответствующих координат x, y, z от параметра t x = x(t); y = y(t); z = kt.(3)

С учетом выражения для параметра t эти уравнения примут форму x = r cosa; y = r sina; z = kra.(4)

При этом длина отрезка винтовой линии при развертке отрезка дуги образующей окружности основания от a до b определяется соотношением

S = Jab V [ x'(t)]2 + [ y'(t)]2 + [ z’(t)]2dt(5)

или

S = f (-r sin a)2 + (r cos a)2 + (kr + rak')2 da.

• A.    Для винтовой линии постоянного шага ( k = const) длина одного витка шнека составит величину [8]

S = f    (-r sin a )2 + (r cos a)2 + (Kr )2Da.

После интегрирования получим

S1 = 2nr>i 1 + k2.

Статистический анализ формы более 150 вариантов шнеков волчков показывает, что угол ф составляет от 30 до 60°, поэтому к изменяется в пределах от 33/^ до V3 , таким образом, длина одного витка винтовой линии находится в диапазоне: S 1 = 2nr х x(1,15 + 2,0).

Для ^ витков расчетная длина винтовой линии эффективного шнека постоянного шага (с учетом требования обеспечения достаточного давления мясного сырья в зоне резания) составит величину

S _^ = 2,0 х ^ х 2пг.                                         (9)

Обычно количество витков шнека волчка находится в пределах 3–6 [7–12]. Для бытовых мясорубок количество витков составляет от 2,5 до 4.

Б. Для винтовой линии с переменным шагом постоянство тангенса угла наклона не выполняется, к = и ar, и для расчета ее длины требуется знание закона изменения к = к(ф( a)) = k(a).

Учитывая зависимость ф = ф(t), а также t = t(a) = r ■ a, получим необходимую зависимость к = k(a).

Как было отмечено, из анализа более 150 моделей волчков от разных производителей следует, что величина ф _Н изменяется в диапазоне 0,5 + 1,0 рад в начальной части шнека. Угол наклона винтовой линии в конечной части шнека ф _к является наиболее ответственным и характеристическим параметром с точки зрения эффективности работы волчка, так как определяет давление мясного сырья в зоне резания. Этот угол составляет, как правило, от 5 до 15°, т. е. от 0,08 до 0,25 рад.

Таким образом, задача корректного описания закона изменения угла наклона винтовой линии по ее длине является в данном случае ключевой для определения зависимости к = k(a).

При изложенных предпосылках для ф _н и ф _к , а также учитывая, что с перемещением от загрузочной горловины волчка к выходной решетке уменьшение шага винта шнека должно происходить с уменьшающейся скоростью, следует, что зависимость ф = ф(a) должна быть нелинейной. Линеаризация этой зависимости позволит увеличить скорость нарастания давления в зоне резания и укоротить длину корпуса волчка [9; 10].

Таким образом, можно принять ф = ф0 - mra,                                          (10)

где m — коэффициент пропорциональности; ф ₀ — начальное значение угла наклона винтовой линии шнека.

Значения ф ₀ и m находим из упомянутых выше граничных условий: — при a = 0; ф = ф _н = 0,5 + 1,0;

- при a = N ■ 2п; ф = ф _к = 0,08 + 0,25.

В результате подстановки получим искомые значения:

Ф о =Ф н ;

m =Ф н

-

ϕk

N ■ 2 n r

•

Соотношение (10) примет вид

ϕ0 = ϕн

-

ϕн

-

N ■ 2n

ϕ k α.

Из требования максимальной эффективности шнекового механизма полагаем ф н = 1,0; ф _к = 0,08. Приняв значение ^ = 4, получаем минимальную величину:

1,0 - 0,08 0,0366

m =-------=-----

8n r

.

r

Тогда, учитывая требование ф _к = 0,08 для наискорейшего обеспечения минимально необходимого давления в зоне резания и принимая полученное значение m, запишем:

ф = 1,0 - 0,0366a.

В таком случае имеется возможность корректного аналитического определения длины винтовой линии шнека с переменным шагом.

Для этого преобразуем соотношение (6) к виду

S = r f V1 + [tg ф + a (tg[( ф ) ' )]] ² d a . 0

С учетом выражения (12) для ф, после несложных преобразований получаем длину винтовой линии как функцию a:

α

S = rf

1 +

0,5 sin(2 - 0,0732а) - 0,0366а cos ² (1 - 0,0366а)

■ D а.

Для удобства вычислений соотношение (16) можно выразить вновь как функцию ф:

S = r Гн

ϕ _k

1 +

0,5sin2 ф- (1 -ф )

cos ф

d ф .

Вычисления показывают, что для ^ витков шнека с переменным шагом винтовой линии ее длина в предложенных граничных условиях для ф н и ф _к может составить величину

S _^ = 1,246 ^ ■ 2 nr.                                          (18)

Сравнение соотношений (18) и (9) показывает, что при использовании шнека с переменным шагом длина его винтовой поверхности изменяется относительно аналога с постоянным шагом на 37,7 %. Таким образом, предложенная методика расчета позволяет существенно повысить точность аналитического определения длины винтовой поверхности шнека. При этом работа сил трения скольжения материала на меньшем перемещении также снижается соответственно на 37,7 %.

На процесс транспортирования мясного сырья шнеком в общем объеме расхода энергии затрачивается, как отмечается в работе [6], около 6,3 %. Таким образом, абсолютное снижение потерь мощности на трение о шнек составит 37,7 % х 6,3 % = 2,3751 %, т. е. около 2,4 %, что представляется при значительных объемах переработки мясного сырья в стране (2 433 тыс. т в 2016 г. только по колбасным изделиям ¹ ) весомой величиной. В пересчете на денежное выражение при удельном потреблении энергии 2,5–12 кВт·ч на тонну продукции [13] эта цифра составит порядка 64 млн руб. в год.

• В.    Длина корпуса Н волчка переменного шага определяется величиной координаты Z винтовой линии шнека. Учитывая соотношения для тангенса переменного угла ф наклона винтовой линии и закона

изменения этого угла от циклической координаты а при известном количестве витков шнека N, запишем следующие определяющие уравнения:

z = kra;(19)

k = tgv;(20)

a = N ■ 2n;(21)

ϕ = ϕ _н

ϕ _н -ϕ_k

N ■ 2n

В таком случае длина корпуса шнека волчка с числом витков N составит величину

Н = tg^ k ■ r ■ N ■ 2п.                                            (23)

Для реального значения ϕ _k , обеспечивающего необходимую скорость подачи материала к режущему узлу ϕ _k = 0,222 рад (около 15º), получаем значение длины винтового шнека

H = 3,3D,                                            (24)

здесь D = 2r - диаметр шнека.

Разработанные теоретические материалы хорошо согласуются с полученными в работах [11; 12] экспериментальными данными для Н эксп , рекомендательно составляющими Н эксп = (3-3,5)D.

Заключение

Таким образом, получены корректные аналитические соотношения для определения конструктивных параметров шнека с переменным шагом и длины корпуса волчка, позволяющие осуществлять их уточненный расчет, практическая реализация которого обеспечивает снижение энергетических затрат на процесс перемещения обрабатываемого материала на 37,7 %, что в общих энергетических затратах составляет 2,4 %. К этим параметрам в первую очередь относятся: начальный угол наклона винтовой линии шнека, конечный угол наклона винтовой линии, закон изменения этого угла, длина винтовой линии шнека, длина корпуса шнека. Полученная модель является основой для корректной постановки и решения задачи "шлюзования".