Математическое моделирование инвазивной карциномы в условиях анизотропии химических полей: почкование и миграция раковых клеток
Автор: Красняков И.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 3 (97) т.26, 2022 года.
Бесплатный доступ
За последнее десятилетие произошли изменения в подходе к изучению злокачественных опухолей. Стало известно, что опухоль является гетерогенным скоплением раковых клеток и в ходе своей эволюции может образовывать различные пространственные структуры для коллективной инвазии и миграции. Одним из процессов, обусловливающих злокачественность, является почкообразование раковых клеток на инвазивном фронте опухоли. Новая парадигма к рассмотрению опухоли и проявляющиеся эффекты при её эволюции требуют изучения не только медицинскими методами, но и методами математического моделирования. Применяя методы математического моделирования при изу-чении злокачественных новообразований, становится возможным взглянуть на процессы в динамике, протекающие во время роста опухоли. В данной работе мы разрабатываем математическую модель роста гетерогенной инвазивной карциномы. В основе модели лежит модель клетки с индивидуальной динамикой, что позволяет нам в определённой степени детально описать исследуемый объект. При моделировании был воспроизведён эффект почкообразования во время роста карциномы криброзного типа. Проведено качественное сравнение с результатами клинических исследований гистологических срезов. Также изме-рена количественная характеристика, индекс эпителиально-мезенхимального перехода, которая сопоставляется с фенотипом клетки в живой ткани. Показана динамика образования клеток-почек, их перемещение возле фронта опухоли и амебоидная миграция в ткани эпителия. Также показано образование вторичного очага опухоли в результате мезенхимально-эпителиального перехода. Результаты исследования позволяют демонстрировать динамику развития злокачественных образований и присущих им эффектов.
Математическое моделирование, раковые структуры, амебоидная миграция, эпителиально-мезенхимальный переход, почкование опухоли, моделирование рака
Короткий адрес: https://sciup.org/146282599
IDR: 146282599 | УДК: 531/534: | DOI: 10.15593/RZhBiomeh/2022.3.03
Текст научной статьи Математическое моделирование инвазивной карциномы в условиях анизотропии химических полей: почкование и миграция раковых клеток
Рак является одной из наиболее распространённых причин смертей в мире. В 2018 г. на его долю пришлось около 9,6 млн. смертей. Заболеваемость раком возрастает по многим причинам [29]. Таким образом, рак является серьёзным и опасным явлением, а борьба с этим заболеванием требует всё больше материаль- ных и интеллектуальных ресурсов.
В настоящее время имитационное математическое моделирование патологических процессов в живом организме является одним из самых актуальных направлений в научных исследованиях сложных живых систем. Дело в том, что медицина всегда имеет дело с уже сформированным организмом и не может видеть внутренние процессы в их динамике. Вот поче-


Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International
License (CC BY-NC 4.0)
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)
му математическое моделирование процессов роста злокачественных опухолей может существенно помочь традиционным методам исследования, а также является одним из важных инструментов в медицинской биологии.
Результаты исследований последних лет говорят о том, что опухоль не является однородным скоплением клеток, которые делятся неконтролируемо. Опухоль представляет собой скорее социум взаимодействующих раковых клеток, которые могут образовывать различные структуры как инвазивного, так и неинвазивного типа [25; 27; 29]. Существуют различные виды классификаций опухоли, но зачастую пользуются единой классификацией ВОЗ, которая регулярно обновляется [25]. Все структурные виды опухолей можно разделить на два качественно разных типа: многоклеточные, которые состоят из большого числа клеток ( N >> 10), и малоклеточные, которые сформированы небольшим числом клеток (даже в пределах одной клетки). К многоклеточным структурам можно отнести солидную, криброзную, папиллярную, микропа-пиллярную и другие [25]. К малоклеточным - альвеолярную, тубулярную, трабекулярную структуры и группы отдельных клеток [10].
Ещё одно подтверждение того, что опухоль является гетерогенным образованием, это наличие « клеток-почек ». Этот гистологический феномен получил название « почкование опухоли » [15]. При этом феномене наблюдаются отдельные раковые клетки и / или их небольшие скопления в строме возле опухоли. Считается, что почкование опухоли связано с плохими прогнозами развития рака [21], так как этот феномен обусловлен эпителиально-мезенхимальным переходом (здесь и далее - ЭМП) раковых клеток. Иногда может встречаться и частичный ЭМП, который аналогичен по своей природе полному переходу, но при этом сохраняются некоторые эпителиальные межклеточные связи. В этом случае совершившие переход клетки приобретают миграционные признаки, в результате чего возникает коллективная клеточная миграция [15]. Широко распространено мнение, что клетки-почки обеспечивают опухоли гистологическую основу для инвазии и метастазирования. При почковании на инвазивном фронте наблюдаются одиночные опухолевые клетки или их группы от 2 до 5 клеток [15; 18; 21]. Так как такие образования могут быть представлены от одной до 5 опухолевыми клетками, то обычно предполагают следующий ход событий. Одиночные опухолевые клетки начинают мигрировать в ткани, так как такие клетки имеют полностью мезенхимальный фенотип, на что указывают исследования [9; 10]. Такие клетки способствуют метастазированию рака молочной железы [28]. А группы опухолевых клеток, в свою очередь, образуют высокоинвазивный фронт и имеют потенциал к метастазированию, что и обусловливает плохой прогноз [21; 28].
Миграция как коллективных групп клеток, так и одиночных клеток обуславливается ЭМП. Этот механизм включается всякий раз, когда клеточной ткани требуется интенсивное движение. В работе [23] описаны механизмы миграции групп клеток. Авторы подразделяют клетки на два типа: лидирующие и следующие за ними. Для совершения успешной миграции групп клеток лидирующие клетки не должны полностью терять адгезионную связь с следующими за ними клетками, т.е. без разрушения десмосомных связей между клетками. Такая картина наблюдается при неполном ЭМП. Тяговые усилия для совершения миграции группы клеток инициируются лидирующими клетками. Замыкающие клетки пассивно подтягиваются по направлению вектора движения. Но, как утверждают авторы работы [23], замыкающие клетки также могут участвовать в создании группового усилия и играть важную роль в организации клеточной миграции. Для одноклеточной миграции характерно наличие отдельных раковых клеток в прилегающей здоровой ткани. Такая миграция использует ряд стратегий, в зависимости от жёсткости адгезивных соединений внеклеточного матрикса, сократимости цитоскелета и способности изменять форму внеклеточного матрикса во время миграции [17].
Что же касается математического моделирования структурообразования и развития злокачественных новообразований, то существует множество моделей. Большие обзоры прошлых работы были представлены в [3; 4; 7]. Например, в работе [17] был использован дискретный подход к построению математических моделей роста опухоли. Авторы представили в работе модель, свободную от вычислительной решётки коллективной миграции клеток с учётом их адгезии, в отличие от классической модели случайного блуждания клеток. Было продемонстрировано структурообразова-ние и миграция коллективных форм злокачественной опухоли. В другой работе [12] была исследована пространственно-временная динамика модели инвазии рака с учётом адгезионных свойств. В модели адгезии «клетка-клетка» и «клетка-матрикс» учитывалась переменными в системе дифференциальных уравнений в частных производных. Изменение адгезионных свойств при росте и развитии рака исследовалось с помощью зависимых от времени характеристик адгезии внутри популяции клеток. Представленная авторами динамика качественно похожа на рост инвазивного злокачественного новообразования, в частности такого, как инфильтративный рак молочной железы. Исследование многоклеточных структур (солидная, криброзная, папиллярная) было проведено в работе [7]. Авторами была продемонстрирована их эволюция. Были определены основные управляющие параметры, при которых возникают эти структуры, исследована динамика роста и расположение клеток в раковом социуме. Что касается исследования образования мало клеточных структур, то здесь в основном рассматривают инвазию дискретных групп раковых клеток и их метастатическое распространение. Так, в работе [13] было рассмотрено метастазирование отдельными раковыми клетками под влиянием ферментов, влияющих на ремоделирование тканей как основного фактора инвазивного распространения. Работа авторов [3] является одной из первых, в которой была изучена динамика структурообразования малоклеточных форм миграции инвазивной карциномы неспецифического типа (здесь и далее - ИКНТ).
Известно, что любая живая ткань, по своему строению является многоуровневой. Многоуровневость живой материи заключается в том, что протекающие в ней процессы являются разномасштабными. В данной работе мы выделяем три характерных масштабных уровня: уровень ядра клетки - микроскопический, уровень клетки - мезоскопический и уровень группы клеток - макроскопический. Но можно встретить работы, которые ещё более детализируют характерные масштабы: например, в работе [20] на субклеточном уровне предложено выделить ещё как минимум три характерных пространственных масштаба самоорганизации последовательности ДНК. При моделировании живой ткани надо помнить, что природа любого биологического объекта едина, и любое дискретное разбиение по характерным масштабам условно и имеет отношение скорее к построению математической модели этого объекта.
В данной работе описан подход к разработке двумерной хемомеханической модели структурообразова-ния инвазивной карциномы, образования клеток-почек и дальнейшей их эволюции. При построении математической модели используется модель деформируемой клетки с индивидуальной динамикой, что позволяет достаточно детально описать функциональную единицу живой материи - клетку. Также представляется возможным отследить динамику конкретной клетки в пространстве эпителиальной ткани, на что будет сделан упор в работе. Используя данный подход к моделированию, становится возможным учесть многоуровневое строение живой материи. Представлены результаты математического моделирования таких процессов, как почкование раковых клеток, которое происходит вследствие ЭМП, миграция раковой клетки в ткани эпителия и образование вторичной опухоли в результате мезенхимально-эпителиального перехода (здесь и далее - МЭП) раковой клетки.
Математическая модель
Существует несколько классификаций эпителиальных тканей, однако наиболее распространена морфологическая классификация, в которой эпителии разделяют по числу слоёв (одно- или многослойные) и форме клеток (плоская, кубическая, призматическая). В однослойном эпителии все клетки лежат на базальной мембране. Если при этом клетки имеют одинаковую форму, т.е. изоморфны, то их ядра расположены в один ряд - это однорядный эпителий. С определенными оговорками такую клеточную ткань можно считать двумерной, что существенно упрощает построение математической модели.
Опишем основные особенности предлагаемой модели. Она включает в себя динамику отдельных клеток, представленных в виде правильных гексагонов. Эта форма заполнения плоскости весьма популярна в природе (пчелиные соты, форма молекулы графена), а также такой многоугольник является одной из популярных форм для заполнения плоскости [8]. Кроме этого, форма гексагона наиболее близка к окружности и является энергетически выгодной формой для клетки. Число сторон многоугольника является индивидуальной особенностью каждой клетки и может динамически меняться в ходе её эволюции. Таким образом, в качестве начального условия для ткани задаётся либо гексагональный паркет, либо плоскость, которая состоит из случайных многоугольников. Система откалибрована таким образом, чтобы наиболее вероятной формой в ходе её эволюции была бы гексагональная форма, но и появление других форм многоугольников не исключено. Клетки плотно примыкают друг к другу, образуя сплошную поверхность без просветов, как и в естественном эпителии (рис. 1). Перечислим минимальный набор свойств, которыми должна обладать разрабатываемая математическая модель:
-
• динамически изменяемые размер и форма клетки в процессе эволюции ткани из-за меняющихся локальных механических свойств среды;
-
• пролиферация клеток ткани при определённых условиях эволюции;
-
• наличие механизма интеркаляции клеток для снятия локальных напряжений в ткани эпителия;
-
• перемещение клеток в ткани эпителия посредством механизма интеркаляции;
-
• обмен химическими сигналами между соседними клетками эпителия через общую границу (см. рис. 1);
-
• конструирование обратных связей между химическими сигналами и биомеханическими свойствами ткани.
Как известно, для поддержания жизни клетки, ей необходимо потреблять питательные вещества, которые поступают как из базальной мембраны, так и ближайшего кровеносного сосуда. Получив необходимое количество вещества, клетка распределяет его остатки между соседними клетками. Хотя процесс переноса веществ в клетках весьма сложный, проще всего смоделировать его с помощью межклеточной диффузии, уравнение которой для каждой клетки можно записать следующим образом:
J . = al Ас - C), ji jiy j i), dC i dt
N 0 ( t )
^ Jji - ^CCi , j =1
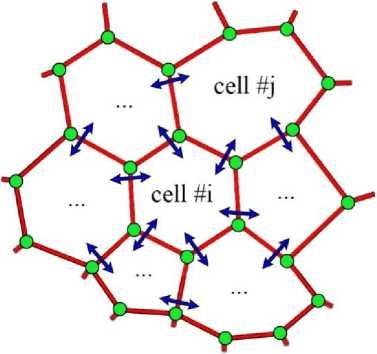
Рис. 1. Схематическое изображение клеток, обменивающихся химическим сигналом
где J ji - поток вещества С из клетки j в клетку i , а - коэффициент диффузии, l ji - длина границы между j - и i -клетками (рис. 1), C i - концентрация вещества, в с — коэффициент деградации, интерпретируемый как скорость потребления питательного вещества или скорость деградации белка. Поле концентраций C не является непрерывным, в связи с тем, что каждая клетка является пикселем поля. Будем полагать, что внутри одной клетки концентрация вещества релаксирует настолько быстро, что в любой момент времени мы можем считать её постоянной в пределах данной клетки. Таким образом, суммирование в слагаемом (2) ведётся по всем соседним клеткам N 0, которые вносят вклад в общий диффузионный поток, число которых для каждой клетки меняется со временем.
Система уравнений вида (1)-(2) позволяет описывать процессы реакции-диффузии и переноса в клеточных ядрах, задавая самый мелкий масштаб (микроскопический) явления в эпителиальной ткани. Обратная связь с биомеханикой среды работает следующим образом: химический сигнал С служит непосредственной командой для изменения локальных механических свойств ткани. В свою очередь механика клетки (изменение формы, деление, интеркаляция) меняет условия для формирования сигнала C и может его как ослаблять, так и усиливать. Так формируется хемоэластичность среды. Для отличия здоровых клеток от клеток раковой опухоли мы вводим дискретную функцию состояния Z, которая принимает только два значения: Z = 0 - здоровая клетка и Z = 1 - раковая клетка. Это позволяет маркировать клетки и задавать в модели два набора значений управляющих параметров, которые определяют совокупность хемомеханических свойств здоровой и опухолевой ткани. Такой подход позволяет иметь доступ к каждому сообществу клеток и производить расчёт напряжений в общей ткани эпителия. Важным элементом предлагаемой модели является представление карциномы как гетерогенного сообщества клеток. Принципиальным инструментом идентификации фенотипа каждой клетки в опухоли является этап ЭМП, на котором находится данная клетка. В клинических условиях фенотип клетки может быть определён с помощью измерения уровня экспрессии интегринов конкретного семейства [9], которые позволяют вычислить индекс ЭМП. В реальной ткани клетка меняет свой фенотип, а затем начинает вести себя соответствующе. В нашей модели этот процесс определяется положением клетки в опухоли и зависит от её окружения. Так мы можем задавать тип поведения для каждой раковой клетки в сообществе. Обозначим индекс ЭМП для i клетки как Ai и нормируем его значение таким образом, чтобы значение Ai = 0 отвечало эпителиальному (здесь и далее - Э) фенотипу, а значение Ai = 1 - мезенхимальному (здесь и далее -М) фенотипу. При этом промежуточные значения соответствуют смешанному эпителиально-мезенхимальному (здесь и далее - ЭМ) фенотипу. Математически вычисление индекса ЭМП для раковой клетки можно определить через функцию состояния Z
A ( t ) = 1 —
N 0 ( t )
1ZL
N 0 ( t ) ’
где N 0 - общее число клеток вокруг раковой клетки (это число сторон многоугольника), а суммирование ведётся по числу соседей. Таким образом, значение функции A определяет фенотип у каждой раковой клетки и принимает дискретные значения, так как количество соседей у любой клетки всегда остаётся конечным, хоть и меняется в ходе эволюции ткани.
Эластичная потенциальная энергия всей эпителиальной ткани задаётся следующим уравнением
E ( t ) = 1 T ( n ( S i ( t ) — S о ) 2 + ^2 ( t ) ) , (4)
где S и P площадь и периметр клетки соответственно, а суммирование ведётся по всем клеткам рассматриваемой системы. Первое слагаемое в скобках формулы (4) представляет собой сопротивление клетки действию сил растяжения и сжатия со стороны среды и её стремление сохранить свою среднюю площадь S о . Коэффициент эластичности среды п является важным параметром модели, определяющим свойства деформации среды. Второе слагаемое отвечает за форму клетки. Параметр μ определяет способность клетки изменять свой периметр. Текущие периметр и площадь клетки являются не постоянными значениями, а меняются в ходе эволюции ткани.
Эпителиальная ткань эволюционирует посредством перемещения узлов клеток. Вектор механической силы, действующей на i -й узел (узлы многоугольника отмечены на рис. 1 зелёными точками), определяется обычным для механики образом - градиент потенциальной энергии (4) по радиус-вектору узла:
F = - i
dE dR
i
где Ri - радиус-вектор i узла. Смещение узлов приводит к изменению периметра и площади клетки.
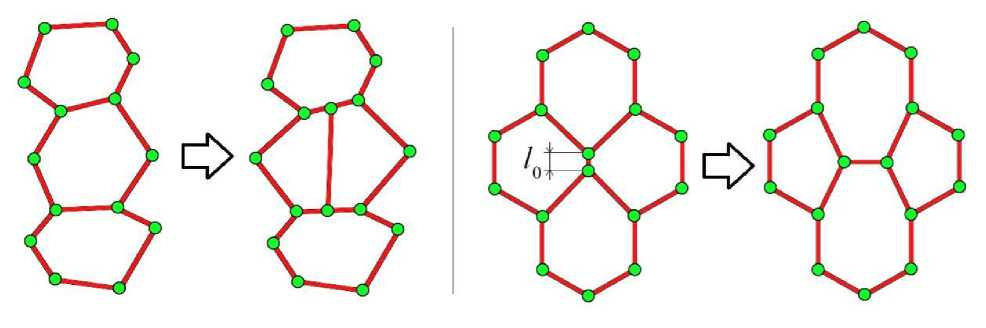
а б
Рис. 2. Механизмы пролиферации ( а ) и интеркаляции ( б )
Остановимся на уравнении движения клеток. В случае здорового эпителия клетки включены в общий пласт, связаны с соседями десмосомными связями и не могут перемещаться по ткани. В этом случае уравнение движения для такой среды не нужно. Но, как было описано выше, клетки иногда получают команду двигаться. Например, такая ситуация складывается при миграции раковых клеток в здоровой ткани или при заживлении раны. Для моделирования движения клеток в эпителиальной ткани наиболее приемлемым аппаратом является механика Аристотеля. В уравнении движения Аристотеля силы напрямую определяют скорость движения объекта. Выбрана механика Аристотеля в связи с тем, что клеточная среда является сильно диссипативной средой, где движение происходит без эффекта инерции. Учитывая это, уравнение для смещения узлов клетки будет выглядеть следующим образом
ему. В центрах этих рёбер ставятся новые узлы, которые соединяются новым ребром. Новая клетка заносится в список, наследует параметры материнской клетки и мгновенные значения химических и механических полей, а затем начинает свою эволюцию в эпителии. Таким образом алгоритм имитирует митотическое деление клеток.
Ещё одно важное свойство эпителия – это процесс интеркаляции. Он необходим для ослабления избыточных локальных напряжений в ткани. При снятии локальных напряжений на временном шаге осуществляется клеточная перестройка, которая уменьшает напряжение по всей ткани [16]. Простейший алгоритм интеркаляции запишем следующим образом
p int
' 1, к < l 0
_ 0, к ^ l 0
d R
V =--- = k F H ii dt
(I Fil- Fo),
где H – функция Хэвисайда, k – коэффициент мобильности, F 0 – критическая сила, ниже которой узел остаётся неподвижным. Здесь F 0 гарантирует, что любое локальное движение в среде начинается, если внешняя сила превышает некоторый порог. Это необходимо для придания общей устойчивости и определённой инертности ткани.
Рассмотрим важное свойство клеточной ткани – деление. Для клеток эпителия в модели предполагается, что их вероятность p деления зависит от количества её узлов
Алгоритм (8) срабатывает каждый раз, если перемычка между клетками становится меньше критического значения l0 (рис. 2, б). Механизмы пролиферации и интеркаляции (см. рис. 2) позволяют клеткам модели динамически менять размер и форму за счёт изменения
n - 6 p = p 0 q
где p 0 и q – параметры задачи. В случае q > 1 деление клеток с большим числом узлов предпочтительно, хотя наиболее выгодной формой клетки остаётся гексагон. Параметр p 0 отвечает за скорость деления всех клеток системы. Процесс деления происходит так, как это показано на рис. 2, а . При выполнении условия деления клетки в ней находится наибольшее по длине ребро и противоположное
количества вершин многоугольника, и их перемещения под действием внешних сил. Таким образом, каждая клетка в модели испытывает ряд хемомеханических воздействий, под влиянием которых она эволюционирует со всей системой.
Обратная связь между процессами реакции-диффузии в клетках (1)–(2) и механикой клеточной ткани, описываемой уравнениями (3)–(8), может быть задана путём установления функциональной зависимости величин μ, η, F 0 , p 0 , q , и l 0 с концентрацией C . Так, ткань начинает проявлять свойства хемоэластомера, механические свойства которого изменяются под влиянием биохимических процессов в клетках и ядрах клеток. Численное моделирование динамической системы (1)–(8) может быть выполнено с помощью подходящей конечно-разностной схемы, в которой временной шаг уравнений реакции–диффузии (1)– (2) должен быть синхронизирован с шагом механической подсистемы (6).
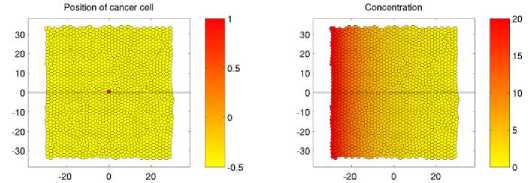
Рис. 3. Состояние сиcтемы в момент времени t = 0. Слева представлено поле состояния клеток A , где A i = 1 соответствует мезенхимальному фенотипу раковых клеток, A i = 0 – эпителиальному фенотипу раковых клеток. Здоровым клеткам было присвоено значение индекса A = –0,5, для того чтобы придать контрастность изображению. Справа – поле концентрации питательного вещества (например кислород), которое распространяется по ткани от ближайшего кровеносного сосуда
Параметры величин математической модели роста карциномы криброзного типа
|
Механические свойства клеток |
|||||
|
η |
μ |
S 0 |
F 0 |
k |
|
|
4,5 |
0,001 |
2,598 |
0,1 |
0,5 |
|
|
Поток питательных веществ |
|||||
|
α |
β C |
||||
|
0,005 |
0,2 |
||||
|
Деление и интеркаляция клеток |
|||||
|
p 0 |
q |
l health |
l cancer |
||
|
0,0002 |
1,4 |
0,1 |
0,4 |
||
Разработанную математическую модель можно классифицировать как сложную дискретную систему, в основе которой лежит модель деформируемой клетки. Модель учитывает индивидуальную динамику отдельных элементов, а также групповые эффекты коллективного поведения.
Результаты математического моделирования
В ходе проведения численных экспериментов начальные условия для каждого случая были практически идентичны. Клеточная ткань состоит из 1560 клеток. В центре помещена одна раковая клетка, в некоторых случаях она была расположена в правой части расчётной области. Основные параметры уравнений (1)–(8) представлены в таблице. В каждом конкретном случае изменяемые параметры для каждого класса клеток бу- дут представлены в соответствующем разделе.
Уравнение для вычисления вероятности деления раковых клеток задаётся феноменологическим выражением и определяется фенотипом клетки и доступом к питательному веществу злокачественную в данной рабо- те не рассматривается.
P,. = P„ + P H div 01
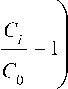
( 1 - A i ) m А П
(1 +(1 - A,.)m )(1 + A) , где P0 – базовая вероятность деления, задаваемая выражением (6), P1 – нормировочный коэффициент, а C0 – пороговое значение питательного вещества.
Почкование раковых клеток от материнской опухоли
Как отмечалось выше, почкование раковых клеток связано с плохим прогнозом развития раковой опухоли [5]. Клетки-почки, приобретая М-фенотип, отделяются от раковой опухоли и дают метастазы, которые повышают риск появления нового очага опухоли после успешного лечения.
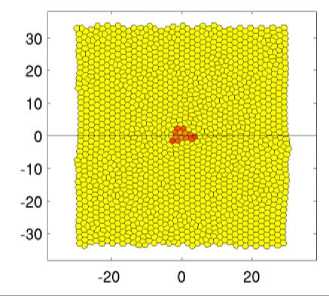
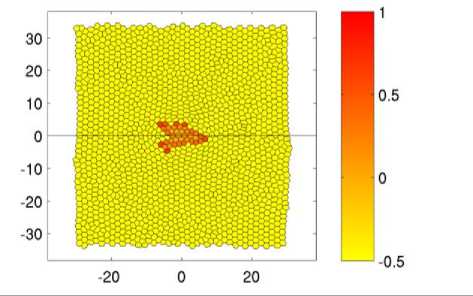
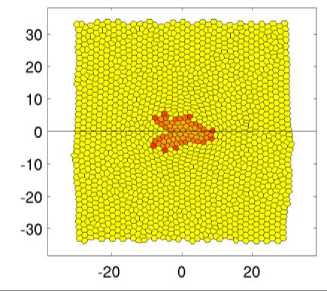
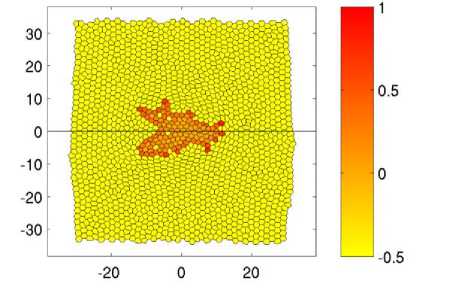
Ниже представлены результаты расчёта (рис. 4), которые показывают динамику структурообразования инвазивной карциномы криброзного типа, на фронте которой происходит почкование раковых клеток. Снимки представлены через равные промежутки времени.
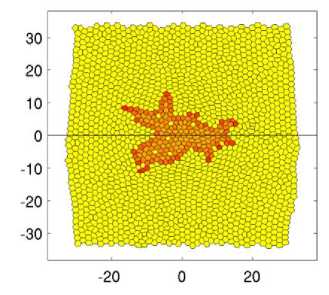
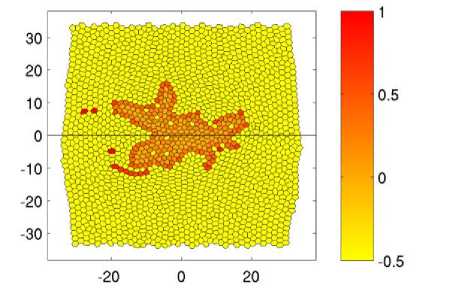
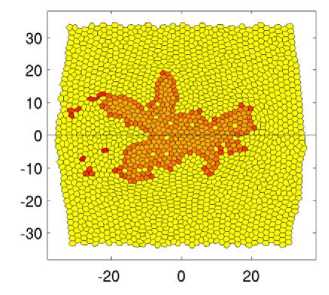
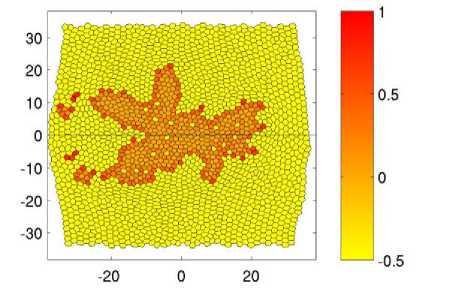
Из снимков (см. рис. 4) видно, что с самого начала опухоль развивается неравномерно. Уже в момент времени t = 60 наблюдается неоднородное развитие карциномы. Две пальцеобразные структуры направлены в сторону источника питательного вещества, а с противоположной стороны опухоль развивается радиальным образом. Далее пальцеобразные структуры продолжают развиваться по градиенту питательного вещества t = 80. Их развитию способствуют клетки, которые находятся на инвазивном фронте. Затем эти отростки увеличиваются в размерах, а клетки, находящиеся на них, с индексом A i , близким к 1, начинают отпочковываться, т.е. претерпевают ЭМП t = 120. В момент времени t = 120 на инвазивном фронте наблюдается трабекулярно-подобная структура [5], которая образуется в результате почкования клеток. Далее, в моменты времени t = 140 и t = 160, отпочковавшиеся клетки мигрируют в ткани к источнику питательного вещества претерпевая акты деления. В результате наблюдается картина, описанная в работе [15]. В ткани возле инвазивного фронта образуются одиночные раковые клетки или их группы, состоящие из 2–5 клеток. Наличие таких клеток усиливает инвазивный рост опухоли, что заметно из представленной динамики. Край опухоли, находящийся ближе к источнику питательного вещества, имеет бо́льшие размеры, чем противоположный край. Об этом свидетельствуют инвазивные пальцеобразные структуры и клетки почки, когда с противоположной стороны инвазивный фронт только начинает развиваться. Также об этом свидетельствует траектория смещения центра масс опухоли, представленная на рис. 5.
Опухоль в модели представлена совокупностью клеток (как и в реальной ткани), которые имеют собственный объём (в рамках модели мы оперируем площадями клеток) в каждый момент времени. Также нам известно положение их центров тяжести.
t = 20
t = 40
t = 60
t = 80
t = 100
t = 120
t = 140
t = 160
Рис. 4. Эволюция криброзной карциномы в моменты времени через равные промежутки. Представлены поля индекса ЭМП ( A i ). Чтобы показать контрастность здоровых клеток на изображении, им было присвоено значение индекса A = –0,5. Параметры, используемые при расчётах, представлены в таблице
Тогда центр масс опухоли можно рассчитать стандартным методом разбиения
X cm
N ( t‘ )
Z St ( t ) xt ( t ) i = 1 у / \ , cm
St total
N )
g S ( t ) yi ( t )
S,, АЛ ’ total
где S i ( t ) - площадь клетки, X i ( t ) и y i ( t ) - центры тяжести клетки, S totai ( t ) - сумма площадей всех раковых клеток, N ( t ) - число раковых клеток в системе. Для каждого момента времени мы можем рассчитать центры масс раковой опухоли X cm и Y cm . График (см. рис. 5) наглядно демонстрирует более интенсивное смещение опухоли по градиенту питательного вещества с момента времени t = 60.
Именно с этого момента времени наблюдается развитие пальцеобразных структур (см. рис. 4), которые можно интерпретировать как образование инвазивного фронта карциномы [5]. Именно с таких участков опухолевые клетки могут переходить от коллективной миграции к миграции одиночными клетками. Установлено, что данный процесс обусловлен ЭМП [5]. В процессе полного ЭМП клетки отделяются от опухолевого массива и движутся в мезенхимальном состоянии. Данный эффект воспроизводится моделью, и его можно наблюдать на рис. 4 t = 120, где присутствуют три клетки мезенхимального фенотипа, движущиеся в направлении к источнику питательного вещества. Также установлено существование области парциального или частичного ЭМП, при котором клетки, сохраняя межклеточные связи, приобретают свойства, необходимые для успешной миграции [5; 15]. Такой эффект также наблюдается при численной реализации математической модели. В силу его проявления образуется трабекулярно-подобная структура (субструктура) рис. 4 ( t = 120).
Понаблюдаем за одной из клеток данной клеточной субструктуры. В момент времени t = 100 (см. рис. 4) видны зачатки трабекулярно-подобной структуры. Появление первой клетки с индексом A i , близким к 1, происходит в момент времени t = 96 (рис. 6). Эта клетка в системе имеет порядковый номер # 1805. В текущий момент времени её индекс ЭМП имеет значение, равное A i = 0,875. Кривая перемещения её центра масс представлена на рис. 6, а цветными точками обозначено значение индекса ЭМП ( A i ).
В момент времени t = 104 эта клетка претерпевает полный ЭМП, но из-за высокой степени инвазивности «отростка», следующего за этой клеткой, она постоянно приобретает промежуточное значение фенотипа, что не даёт ей приобрести полностью М-фенотип. Таким образом, можно заключить, что эта клетка претерпевает парциальный ЭМП, что и наблюдается в интервале времени t е (108 : 122). Из рис. 6 по значениям индекса ЭМП (Ai) видно, что в этом интервале оно меньше 1 (Ai е (0,75 : 0,875)), что соответствует промежуточному фенотипу. Сама же клетка, имея значение фенотипа меньше 1, переместилась к источнику питательного ве- щества примерно на 5 единиц (см. рис. 6). Это говорит о том, что клетка перемещалась в ансамбле клеток, а значит этот ансамбль претерпел парциальный ЭМП, который описан в работе [15]. Далее хорошо видно из рис. 6, как наблюдаемая нами клетка претерпела полный ЭМП во временном интервале t е (122 : 134), чему соответствует её быстрое перемещение за короткий промежуток времени и её значение функции Ai (t) = 1. Затем эта клетка прекращает своё перемещение и претерпевает МЭП, о чём свидетельствует отсутствие изменения положения и уменьшение индекса Ai до значений, соответствующих эпителиальному фенотипу клеток.
Перемещение раковой клетки мезенхимального фенотипа в ткани эпителия
Как известно, микроорганизмы часто двигаются по градиенту химического вещества - данное явление получило наименование хемотаксис [2]. Подобное явление известно и для клеток [1]. Известно, что клетки в тканях выбирают направление движения по градиенту белковых полей [6; 19; 22; 26] . Например, при заживлении ран механизм генной регуляции, получая сигнал о ранении, включает синтез МАПК (митоген-активируемая проте-инкиназа). Волна этого белка, распространяясь от клетки к клетке, проводит ожижение клеточного слоя, примыкающего к ране. Десмосомные связи между клетками разрушаются, и клетки приходят в движение. Так начинают затягиваться края раны, а в дальнейшем происходит восстановление целостности покрытия [24]. Другими примерами, где направление движения клеток играет важную роль, являются морфогенез [22; 27] и распространение опухоли [5; 10; 27]. Ниже будет приведён результат работы математической модели, который демонстрирует перемещение М-раковой клетки в эпителиальной ткани по градиенту питательного вещества.
Расчётная область имеет квадратную форму и состоит из 1560 гексагональных клеток. На левой границе расчётной области задаём постоянный поток (1) питательного вещества (см. рис. 3 справа). А на правой стороне расчётной области расположим М-клетку, за которой проводится наблюдение (см. рис. 7). Все остальные клетки имеют Э-фенотип. Движущуюся клетку рассмотрим как несжимаемую. В связи с этим предположением коэффициент р в уравнении (3) равен нулю. Такое предположение связано с тем, что, оперируя многоугольниками, появление геометрических фигур с отрицательными углами приведёт к нарушению расчётной сетки. Таким образом энергия клетки зависит от слагаемого, которое отвечает за сопротивление клетки растяжению и сжатию. Что же касается перемещения клетки в модели, то в его основе лежит механизм модифицированной интеркаляции. Опишем подробнее алгоритм движения клетки.
Клетка должна «чувствовать», с какой стороны поступает поток питательного вещества. Мы определяем это следующим образом. Рассчитываем поток питательного вещества в М-клетке.
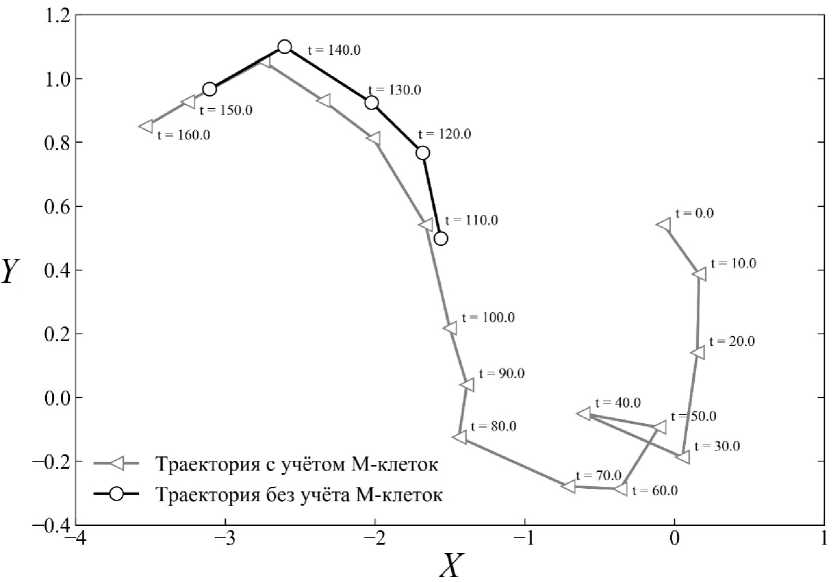
Рис. 5. Траектория смещения центра масс инвазивной карциномы. Серой линией показана траектория с учётом отпочковавшихся клеток, чёрной - траектория без учёта отпочковавшихся клеток
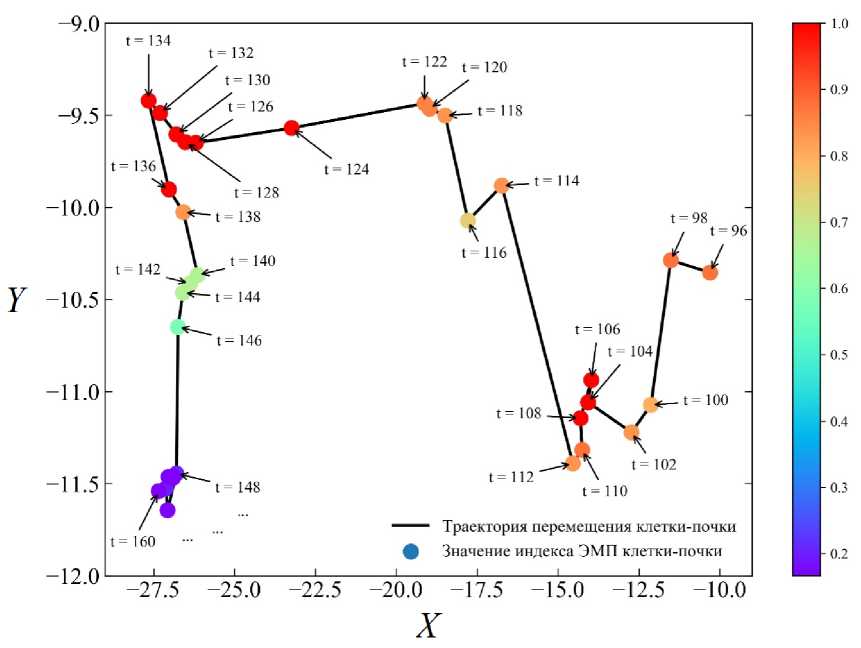
Рис. 6. Траектория перемещения центра масс клетки-почки под номером # 1805 и её изменение индекса ЭМП ( A i ), отмечено цветными точками в разные моменты времени
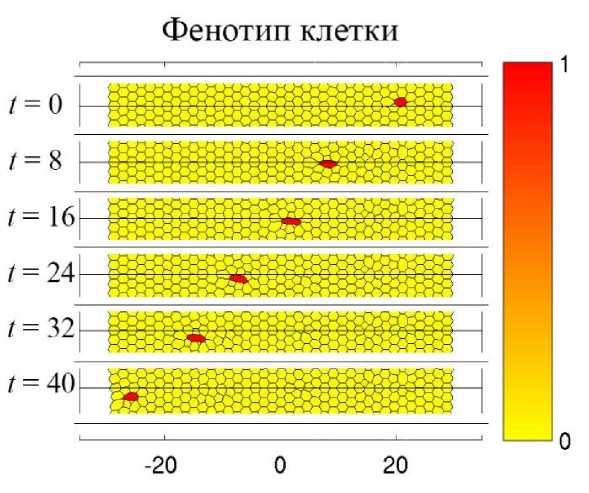
Рис. 7. Поле функции состояния клеток ( Z в разные моменты времени. Z = 0 соответствует здоровой клетке, Z = 1 -раковой клетке. Параметры для здоровых клеток: п = 1,0; q = 0,0; l о = 0,2; остальные параметры представлены в таблице; для раковых клеток: п = 6,0; ц = 0,0; q = 0,0; l 0 = 1,0
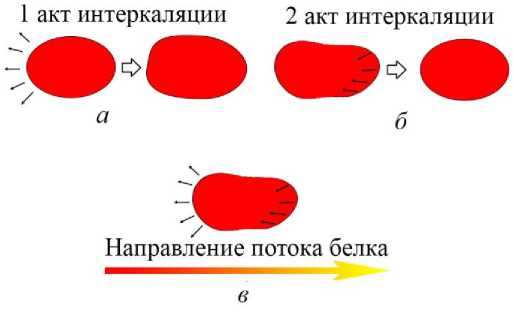
Рис. 8. Схематическое изображение ( а - в) перемещения клетки в модели
Сторона, через которую поток положительный и максимальный, является ближней к источнику питательного вещества. С этой стороны происходит первый акт интеркаляции клетки (рис. 8 , а ), т.е. клетка вытягивается к источнику питательного вещества. Второй акт интеркаляции происходит с противоположной стороны, так клетка подтягивается, сохраняя свою среднюю площадь S 0 (рис. 8, б) . За счёт таких выпячиваний и сокращений происходит ретракция клетки в ткани. Описанный механизм иллюстрирует амебоидный тип миграции клетки в эпителии (рис. 8, в ) по градиенту питательного вещества [1; 19; 26].
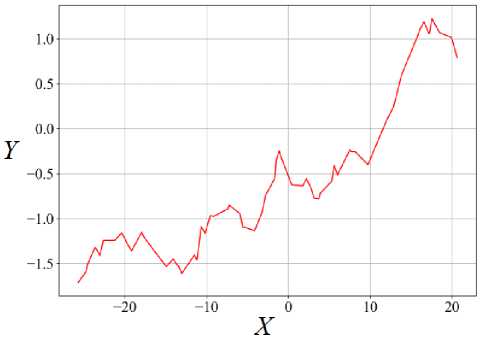
Перемещение клетки в однородной среде происходит с наименьшим отклонением от направления потока питательного вещества. Об этом можно судить по траектории движения клетки (рис. 9, а ).
Учитывая, что диаметр клетки (гексагона) в начальный момент времени равен двум единицам, то её смещение по оси Y на всём пути миграции произошло всего на один клеточный размер, в пределах Y е (1 , -1,5).
МЭП раковой клетки
Процесс, МЭП раковой клетки является механизмом, порождающим вторичные очаги опухолеобразования -метастазирование. Его можно рассматривать как продолжение почкообразования, которое происходит вследствие ЭМП и амебоидной миграции клетки-почки в ткани. На рис. 10 через равные промежутки времени представлен процесс МЭП раковой клетки амебоидного типа.
Для успешного метастазирования раковая клетка должна найти место с достаточным количеством питательного вещества и осуществить МЭП для начала пролиферации. Амебоидное продвижение клетки в ткани эпителия представлено на рис. 7. В представленном примере (см. рис. 10) такое перемещение заканчивается делением клетки, задаваемым выражением (9). При этом значение индекса A i для клетки уменьшается, и она по необходимости совершает МЭП в ходе дальнейшей пролиферации. Так постепенно формируется вторичная карцинома криброзного типа.
а
б
в
г
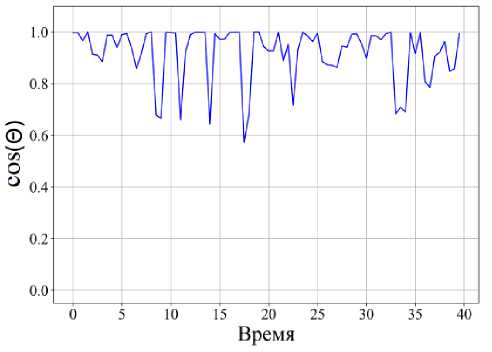
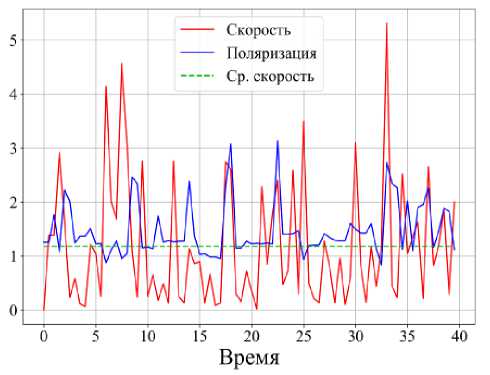
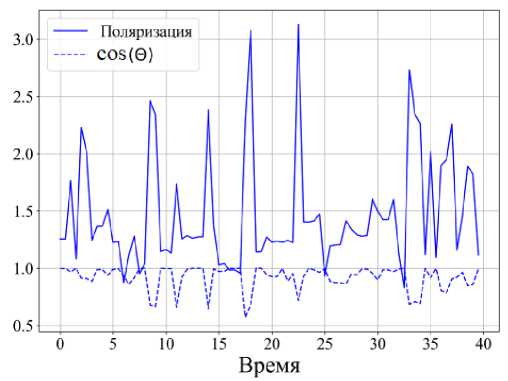
Рис. 9. Графики: траектория перемещения клетки ( а ); отклонение от направления градиента потока питательного вещества ( б ); скорость и коэффициент поляризации ( T ) клетки ( в ); отклонение от направления градиента потока питательного вещества и коэффициент поляризации клетки ( г )
Заключение
В работе представлена дискретная хемомеханическая математическая модель роста инвазивной карциномы как гетерогенного образования, которая учитывает эпителиально-мезенхимальный переход (ЭМП) и обратный к нему мезенхимально-эпителиальный переход (МЭП) раковых клеток. Результатом работы разработанной математической модели является возможность демонстрации динамики развития злокачественной структуры в эпителиальной ткани. В работе представлены и исследованы процессы: почкования раковых клеток в следствии ЭМП; амебоидной миграции раковой клетки в ткани эпителия; метастазирования, МЭП раковой клетки с последующим образованием вторичного очага карциномы.
Финансирование. Данная работа была финансово поддержана Российским фондом фундаментальных исследований (грант № 20-31-90024).
Список литературы Математическое моделирование инвазивной карциномы в условиях анизотропии химических полей: почкование и миграция раковых клеток
- Воротников А.В. Хемотаксис: движение, направление, управление // Успехи биологической химии. - 2011. -Т. 51. - С. 335-400.
- Ермилова Е.В. Подвижность и поведение микроорганизмов. Том 1. Прокариоты / Е.В. Ермилова, Ж.М. Залуцкая, Т.В. Лапина. - СПб.: Изд-во С.-Петерб. ун-та, 2004. - 192 с.
- Красняков И.В., Брацун Д.А. Математическое моделирование формирования малоклеточных групп инвазивной карциномы неспецифического типа // Российский журнал биомеханики. - 2021. - Т. 25, № 2. - С. 173-185.
- Красняков И.В., Брацун Д.А., Письмен Л.М. Математическое моделирование роста карциномы при динамическом изменении фенотипа клеток // Компьютерные исследования и моделирование. -2018. - Т. 10, № 6. - С. 879-902.
- Крахмаль Н.В., Завьялова М.В., Денисов Е.В. Инвазия опухолевых эпителиальных клеток: механизмы и проявления // Acta Naturae. - 2015. - Т. 7, № 2. - С. 1831.
- Ambrossi D., Gamba A. Cell directional and chemotaxis in vascular morphogenesis // Bull. Math. Biol. - 2004. -Vol. 66. - P. 1851-1873.
- Bratsun D.A., Krasnyakov I.V., Pismen L.M. Biomechanical modeling of invasive breast carcinoma under a dynamic change in cell phenitype: collective migration of large groups of cells // Biomechanics and Modeling in Mechanobiology. - 2019. - Vol. 19. - P. 723-743.
- Chavey D. Tilings by regular polygons - II: a catalog of tilings // Computers & Mathematics with Applications. -1989. - Vol. 17. - P. 147-165.
- Denisov E.V., Gerashchenko T.S., Zavyalova M.V., et al. Invasive and drug resistant expression profile of different morphological structures of breast tumors // Neoplasma. -2015. - Vol. 62. - P. 405-411.
- Denisov E.V., Skryabin N.A., Gerashchenko T.S. et al. Clinically relevant morphological structures in breast cancer represent transcriptionally distinct tumor cell populations with varied degrees of epithelial-mesenchymal transition and CD44+CD24- stemness // Oncotarget. - 2017. - Vol. 8, N. 37. - P. 61163-61180.
- Dilao R. Mathematical models of morphogenesis // ITM Web of Conferences. - 2015. - Vol. 4. - Art. 01001.
- Domschke P., Trucu D., Gerisch A., et al. Mathematical modelling of cancer invasion: Implications of cell adhesion variability for tumour infiltrative growth patterns // Journal of Theoretical Biology. - 2014. - Vol. 361. - P. 41-60.
- Franssen L.C., Lorenzi T., Burgess A., et al. A Mathematical Framework for Modelling the Metastatic Spread of Cancer // Bull. Math. Biol. - 2019. - Vol. 81. -P. 1965-2010.
- Friedl P., Locker J., Sahai E., et al. Classifying collective cancer cell invasion // Nat. Cell. Biol. - 2012. - Vol. 14, N. 8, - P. 777-783.
- Grigore A.D., Jolly M.K., Jia D., et al. Tumor Budding: The Name is EMT. Partial EMT // Journal of Clinical Medicine. - 2016. - Vol. 5. - Art. 51.
- Guillot C., Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis // Science. - 2013. - Vol. 340. - P. 1185-1189.
- Johnston S.T., Simpson M.J., Plank M.J. Lattice-free descriptions of collective motion with crowding and adhesion // Phys. Rev. E. - 2013. - Vol. 88. - Art. 062720.
- Koelzer V.H., Zlobec I., Lugli A. Tumor budding in colorectal cancer-ready for diagnostic practice? // Human Pathology. - 2016. - Vol. 47. - P. 4-19.
- Lammermann T., Sixt M. Mechanical modes of 'ameboid' cell migration // Curr. Opin. Cell Biol. - 2009. - Vol. 21. - P. 636-644.
- Lesne A., Foray N., Cathala G., Forne T., Wong H., Victor J.-M. Chromatin fiber allostery and the epigenetic code // J. Phys. Condens. Matter. - 2015. - Vol. 27. - P. 064114.
- Lugli A., Karamitopoulou E., Panayiotides I., at al. CD8+ lymphocytes/tumour-budding index: an independent prognostic factor representing a 'pro-/anti-tumour' approach to tumour host interaction in colorectal cancer // British Journal of Cancer. - 2009. - Vol. 101. - P. 13821392.
- Netti P.A., Baxter L.T., Boucher Y., et al. Macro- and microscopic fluid transport in living tissues: application to solid tumors // AIChE Journal. - 1997. - Vol. 43. - P. 818-834.;
- Roberto M., Sandrine E.-M. The front and rear of collective cell migration // Nat. Rev. Mol. Cell. Biol. -2016. - Vol. 17. - P. 97-109.
- Salm M., Pismen L.M. Chemical and mechanical signaling in epithelial spreading // Phys. Biol. - 2012. -Vol. 9, No. 2. - P. 026009-026023.
- Sinn H.P., Kreipe H. A brief overview of the WHO classification of breast tumors, 4th edition, focusing on issues and updates from the 3rd edition // Breast Care. -2013. - Vol. 8(2). - P. 149-154.
- Stinner B., Bretschneider T. Mathematical modelling in cell migration: tackling biochemistry in changing geometries // Biochem. Soc. Transactions. - 2020. - Vol. 48. - P. 419-428.,
- Tabassum D.P., Polyak K. Tumorigenesis: it takes a village. // Nat. Rev. Cancer. - 2015. - Vol. 8. -P. 473-483.
- Tashireva L.A., Zavyalova M.V., Savelieva O.E., et al. Single Tumor Cells With Epithelial-Like Morphology Are Associated With Breast Cancer Metastasis // Front. Oncol. - 2020 - Vol. 10. - Art. 50.
- World Cancer Report Cancer research for cancer prevention / Edited by C.P. Wild, E. Weiderpass, B.W. Stewart - IARC, 2020. - 611 p.


