Математическое моделирование эффективных упругих параметров

Сейсмическая анизотропия является актуальным объектом исследований в теории сейсморазведки. Анализ связи сейсмической анизотропии (как меры упорядоченного строения) с внутренним строением горной породы представляет собой важную задачу для практики сейсморазведки и интерпретации результатов полевых работ. Существует два. подхода, введения анизотропии скорости распространения упругих волн: первый основан на осреднении закона Гука (динамический), второй - на вычислении скоростей на основе решения уравнения эйконала (кинематический). В работе показано, что эти скорости не совпадают для наиболее простой модели анизотропии -квазианизотропии, появляющейся в результате естественного осреднения тонкослоистой среды.

Первый подход можно подразделить на две части - первая связана с аппроксимацией микронеоднородной упругой среды, заданной моделью вида, материальных уравнений (законом Гука), которая требует определения окрестности компакта, т.е. вида, материальных уравнений. Этот подход развивается И.О. Баюк и изложен в ее докторской диссертации [1]. Другая часть связана с осреднением закона Гука микронеоднородной упругой среды с учетом длины сейсмической волны [2-4]. В последнем случае, для наиболее простой одномерной тонкослоистой модели среды, пачки переслаивающихся пропластков, получен осредненный закон Гука, который провидит к

П.Н. Александров, В.Н. Кризский анизотропии упругих параметров или, как принято в литературе по сейсморазведке, к квазианизотропии. Для такой модели материальных уравнений можно найти решение прямой задачи для уравнений Ламе и провести исследования влияния анизотропии на волновое поле в наземной сейсморазведке.

В общем случае, связь напряжений и деформаций в законе Гука, которая в векторном представлении будет иметь вид Р = Не, где Р - 9-ти компонентный вектор напряжений, е - 9-ти компонентный вектор деформаций, является линейной и описывается матрицей упругих параметров Н размерности 9x9 элементов, которая может зависеть от временной частоты в частотной области и, таким образом, описывать дисперсию упругих параметров.

1. Решение прямой задачи сейсморазведки для слоисто-анизотропных сред

Решение прямой задачи для анизотропных сред не является тривиальным, если использовать стандартный подход к решению уравнений Ламе - как сведение к дифференциальным уравнения второго и более высокого порядка. С другой стороны, все математические модели физических полей являются системами дифференциальных уравнений первого порядка в частных производных, для которых разработаны эффективные математические методы решения.

Рассмотрим модель горизонтально-слоистой анизотропной геологической среды в декартовой системе координат с осью z, направленной вглубь Земли. Вводя вектор

P_S z

X =

, где Pz - 3-х компонентный вектор напряжений, появляющийся под действием вертикальных сил, S - вектор смещений, и применяя преобразование Фу рье по горизонтальным координатам х, у и по времени t, систему уравнений Ламе для этой модели можно свести к виду

IX = A X, ∂z где А - квадратная матрица, включающая упругие параметры среды, пространствен ные частоты kx, ky и временную частоту. Решение этой системы выражается через функцию (экспоненту) от матрицы.

Продолжая поле X через горизонтально слоистую среду от дневной поверхности

до подошвы последнего слоя, получим X n ( z n ) =

(Д1 e A * *)

X ⁰ , где h j

- толщина

j-то слоя, n - номер последнего сло^i бесконечной толщины. X⁰ - вектор-столбец.

заданный на дневной поверхности, z n - глубина залегания последней границы, A ^j -

передаточная матрица j -ro слоя. Поскольку плоскость z = z ₀ совпадает с поверхностью Земля/Воздух, то выполняется условие X¹( z ₀) = X⁰.

В нижнем слое бесконечной толщины, основываясь на знаке действительной части собственных значений матрицы A n, из представления X n ( z ) = e An ^{( z-z} n )X n ( z n ) выделим решение X ^- , возрастающее при z ^ + то, и решение X+, убывающее при z ^ + то : X n ( z ) = X⁺ + X — . Удовлетворяя условию на бесконечности, необходимо положить X⁺ = CSC^{- 1}X n ( z ) = 0 везде, в том числе п при z ^ z n . Здесв C - матрица, составленная из собственных векторов матрицы A n, a S - матрица, получающаяся

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ из единичной матрицы заменой диагональных элементов нулем, если действительная часть соответствующего собственного значения меньше нуля, и единицей, если действительная часть соответствующего собственного значения больше нуля.

Отсюда вытекает связь между компонентами поля X 0: CSC - 1 X n ( z ) =

CSC- ¹ (ц¹ e^A h j^ X 0 = D X 0 = 0 , D = (

d ₁₁ d ₁₂

d 21 d 22

^ , Z = ^—d 11

¹ d 12 = -d 21

1 d 22-

На дневной поверхности зададим сторонние напряжения P z = P Zt (например, в виде плиты вибратора конечных (реальных) размеров), тогда решение поставленной задачи будет иметь вид S = Z- 1 P Zt . При этом никаких ограничений на структуру матрицы упругих параметров не накладывается, и, кроме этого, она может быть

частотно зависимая.

Используя обратное преобразование Фурье по пространственным и временной частотам, можно перейти в пространственно-временную область.

Вычислительные эксперименты проведены для модели трехслойной среды (рис. 1), у которой второй слой является макроанизотропным и эффективные параметры которого являются результатом осреднения тонкослоистой среды с параметрами прослоек указанных в таблице. В таблице использованы следующие обозначения: h - толщина пропластка. V p - скорость продольных воли в слое. V s - скорость поперечных волн в слое, р - плотность горной породы в слое.

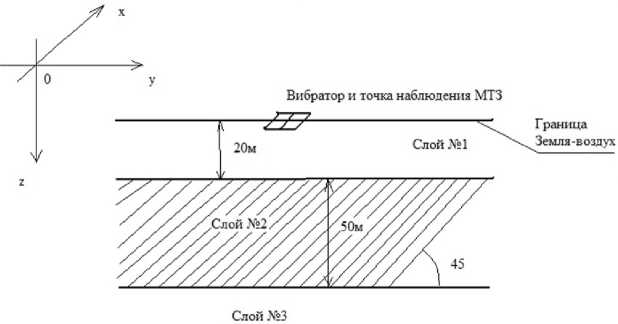
Рис. 1. Модель трехслойной среды с квазианизотропным вторым слоем. Параметры квазианизотропии вычислены в результате осреднения тонкослоистой среды, с наклоном слоистости под углом 45 ° к о си у

Таблица

Параметры тонкослоистой пачки

h, м	V p , м/с	V s , м/с	р, кг/м3
0,01	565,6854	332,7561	2000
0,02	126,4911	74,4065	2000
0,03	565,6854	332,7561	2000
0,01	126,4911	74,4065	2000
0,02	565,6854	332,7561	2000

П.Н. Александров, В.Н. Кризский

Для каждой прослойки второго слоя вычислялись параметры Ламе по формулам: А = р ( V p ² — 2 V s 2), д = pV s 2. После чего проводилось осреднение и осуществлялся / 1        0          0

поворот с направляющими косинусами I 0 0 , 7071 — 0 , 7071 0 0 , 7071    0 , 7071

В случае воздействия на среду импульсом сторонних вертикальных напряжений, заданных по площадке 1x1 м в начале координат с формой, представленной на рис. 2, вычислительным экспериментом получено сейсмическое поле, фрагмент вертикальной компоненты которого изображен на рис. 3. Здесь: момент времени t = 0 , 31 с, площадка измерений - квадрат на плоскости z = 0 размерами 120x120 м с центром в начале координат.

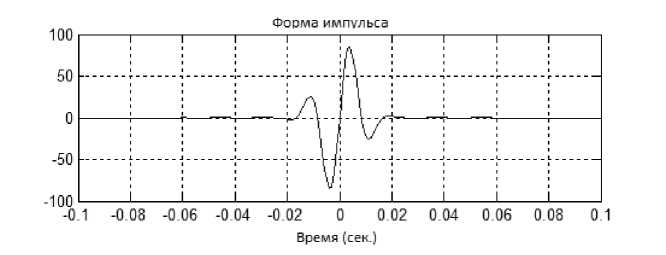
Рис. 2. Форма импульса для сторонних вертикальных напряжений, заданных по пло щадке 1x1 м в начале координат

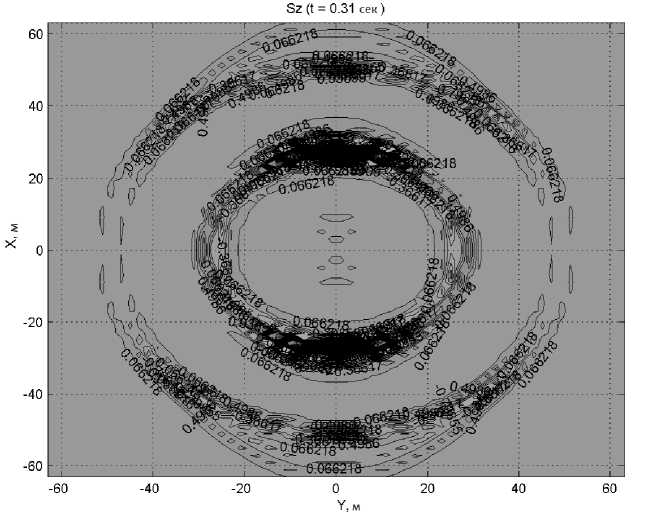
Рис. 3. Фрагмент вертикальной компоненты сейсмического поля, рассчитанного в момент времени t = 0 , 31 с по площади 120x120 м

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Вычислительный эксперимент показывает, что анизотропия проявляется на преломленных волнах в виде эллипса, равных величин смещений, влизи же источника -в виде круга с разной амплитудой по азимуту.

2. Соответствие эффективных сейсмических скоростей

их средневзвешнным величинам

Сейсмическая анизотропия понимается как анизотропия сейсмических скоростей.

С использованием преобразования Фурье по пространственным координатам, оставляя производную по времени для однородной анизотропной среды, можно, анализи руя три компоненты вектора смещения, рассмотреть скорости распространения упру-

-

-

того поля по всем трем направлениям, которые подчиняются волновому уравнению.

В однородном анизотропном пространстве уравнения записать в виде

теории

упругости можно

S = ¹ M S ’ dt

ρ где M = D * H * E, D =

ikx	iky	ik z	0	0	0	0	0	0
0	0	0	ik x	ik y	ik z	0	0	0
0	0	0	0	0	0	ik x	ik y	ik z

H

= c ij •

ik_x [1]

i,j = 1 , 9. E = ik y [1] ik z [1]

«

ikx

Для случая плоской волны, распространяющейся = ik y = 0. отсюда,

в направлении

оси

г.

имеем

ikx

iky

1 dt ^2S      k z р

V z =

/ <  ¹ > ^µ

122 , 878

< - >

µ

122 , 878 0

<

0 S ,

—¹— >  ^{— 1}

А +2 ц >   /

208 , 8932

.

Для случая плоской волны, распространяющейся в направлении = ik z = 0. отсюда,

д^ 2 ^S = -k y²

ρ

<µ> о <

А +2 ц

> _1_ < — ^А — >² ./ —¹— ^—, ¹

> ⁺ <  А +2 ц > <  А +2 ц >

оси

У-

имеем

V y

275 , 0695 0 0

0 449 , 5187 0

122 , 878

.

Для случая плоской = ik z = 0. отсюда,

д ²          „ 1     <

№ ^S = ^-k x Р (

< ¹ > ^µ

S ,

— 1

волны, распространяющейся в направлении оси х, имеем

^{4 ц (} А + ^ц )     । А \ 2 / ¹ \ — 1

А +2 ц >  ⁺ <  А +2 ц > <  А +2 ц >

<µ> 0

0         S ,

< ¹ > ^{— 1}

µ

П.Н. Александров, В.Н. Кризский

	449 , 5187	0	0
V x = I	0	275 , 0695	0
	0	0	122 , 878

Анализируя коэффициент волнового уравнения, который характеризует материальные свойства вещества (горной породы), получены скорости, количество которых равно 9, из которых 5 равны друг другу. В результате, в анизотропной среде распространяются волны с разными скоростями в разных направлениях. Для рассматриваемой модели независимых скоростей четыре: V_p ¹ = 449 , 5187 м/с, V s ¹ = 275 , 0695 м/с, V_p ² = 208 , 8932 м с. V s ² = 122 , 878 м с.

С другой стороны, можно вычислить скорости, основываясь не на динамическом подходе (через уравнения Ламе), а на кинематическом подходе (через средние скорости и средние интервальные скорости). Для средних скоростей, вычисленных на основе уравнения эйконала, получим:

< Vp>T = 5 i=1 hiVP = 419, 2873 м/с ■ < Vp>m = 1 5 hi i-1 = 262, 2096 м c 5 hi i-1 5 hi i -1 v> =5 ∑ hi i i-1 vp < Vs>t = 5 hiVsi i-1 = 246,6396 м/с , < Vs >m = 5 ∑ hi i-1 1 5 hi i-1 = 154,2409 м c. 5 hi i-1 5 hi i -1 vi =5 ∑ hi i i-1 vs hi i =1

Эти величины скоростей не совпадают со скоростями, полученными по осреднению закона Гука.

Кинематический подход по вычислению анизотропии скоростей не применим в случае, если длина волны будет превышать толщину пропластка. Эмпирические оценки толщины пропластка дают толщины, составляющие значения, меньшие 0,1 длины волны. В противном случае анизотропия скоростей не будет соответствовать физике процесса.

Можно предложить следующий алгоритм вычисления анизотропии в кинематическом подходе. По скоростям и плотности заданной тонкослоистой модели перейти к параметрам Ламе, провести осреднение закона Гука, найти скорости и использовать их для анализа кинематики (годографов) распространения сейсмического импульса (фронта волны) на основе уравнения эйконала.

• 3.    Уравнения эйконала в произвольно-анизотропной неоднородной среде

В произвольно-анизотропной и неоднородной среде уравнения эйконала являются собственными значениями матрицы размерности 3x3 [5]:

	/ grad t   [0]     [0] \ T / grad t [0]     [0] \      / 10 0 \
A =	1 [0] grad t [0] 1 Я 1 [0] grad t [0] 1 _ P 1 0 10 1 у [0]      [0] grad t /       у [0]      [0] grad t /        у 0 0 1 /

Следовательно, в произвольно-анизотропной и неоднородной среде имеется три уравнения эйконала вида

(grad t ) T V grad t = 1 .

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Матрицу упругих параметров можно представить в виде составной матрицы

h11 h12 h13 H = h21 h22 h23 h31 h32 h33 где подматрицы hj являются матрицами размерности 3x3. При этом, исходя из структуры матрицы A, в построении уравнений эйконала будут участвовать только диагональные подматрицы h 11, h22, h33. Остальные подматрицы матрицы упругих параметров не участвуют в формировании скорости распространения упругого поля.

Рассмотрим решение уравнения эйконала. Пусть матрица связана с одной из подматриц h 11 . h 22 it ли h 33. Решение уравнен ня эйконала, вида, (grad t ) T V grad t = 1. где матрица, V размерности 3x3 представима, в виде V = v [ А ] v- 1. Здесь лштрпца v есть матрица, составленная из собственных векторов матрицы V , диагональная матрица

0    0

А 22 0 0 А 33

λ 11

[ А ]=    0

• - есть матрица собственных значений матрицы V.

Пусть в однородной среде имеет место соотношение gradt = vgradt, тогда функция t будет удовлетворять уравнению эйконала вида gradtT Vgradt = gradtT v-1 Vvgradt = gradtT [А]gradt = 1.

Или

^А “⁽6 ^{)2 + А} 22 ⁽ ly ^{)2 + А} 22 ⁽ dZ ⁾² = 1 .

Откуда, t=

vA n x ²⁺

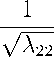
У ² +

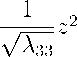
Следовательно, поверхностью изохрон является трехосный эллипсоид. В общем случае их три. При этом, вдоль каждой оси эллипсоида, поле будет распространяться со своими, в общем случае не равными друг другу, скоростями, всего которых девять.

Заключение

Рассмотренные два, подхода, к введению анизотропии скоростей наталкиваются на проблему правильного определения этих скоростей. Для эффективного использования кинематического подхода, к описанию распространения сейсмического поля в произвольно анизотропной неоднородной среде необходимо использовать три уравнения эйконала. Представленный выше результат вывода этих уравнений позволяет конструктивно определять анизотропию скоростей при кинематическом подходе. В общем случае, для произвольно анизотропной среды количество скоростей, определяемых по уравнениям эйконала, равно девяти. Это обобщает доминирующее в настоящее время представление о том, что в анизотропной среде распространяются всего три волны - две поперечные с разными скоростями и одна, продольная.

П.Н. Александров, В.Н. Кризский

Приведенный результат расчета сейсмического поля, зарегистрированного на дневной поверхности, в случае наличия анизотропного объекта приводит к сложной картине волнового поля. Это означает, что необходимо совершенствовать методики сейсморазведки при изучении анизотропных свойств геологической среды.