Математическое моделирование экономической структуры общества на примере статистических данных по Пермскому краю

П од экономической структурой общества (ЭСО) вслед за Д.С. Чернавским будем понимать распределение элементов общества по ликвидным накоплениям [1].

Накопления населения относятся к группе синтетических показателей уровня жизни – важнейшей итоговой характеристике взаимодействующих социальных процессов. Расчеты ЭСО представляют большой практический интерес для анализа матери- ального положения населения, характеристики степени расслоения общества по имущественному состоянию [2]. Также информация о распределении накоплений может использоваться в вопросах определения оптимальной системы налогообложения, ценообразования, адресной безынфляционной эмиссии денег [3–4], формирования банковской политики и в целом макроэкономической политики государства или региона [5–6].

ЭСО в развитых странах можно получить с помощью анализа структуры рынка вкладов в банках [7–9]. Основная причина невозможности применения такого подхода в России кроется в том, что накопления населения преимущественно находятся в неорганизованном виде [10]. С помощью социологических опросов была получена приблизительная оценка количества граждан, имеющих вклады в банках, согласно которой срочные вклады от 10 тыс. руб. принадлежат 25 млн человек, что составляет 17% населения, и на них приходится 99% всех вкладов [11]. Кроме того, в нашей стране информацией по вкладам владеет только агентство по страхованию вкладов (АСВ). При этом оно собирает с банков отчетность по суммам вкладов, а не по вкладчикам. Отметим также, что в понятие «вклады» включаются депозитные сертификаты, средства на разных счетах, в том числе «карточных» и т.д. Понятно, что у одного и того же человека могут быть и минимальные, и средние, и максимальные остатки на счетах одновременно. Следовательно, даже имея статистику по вкладам АСВ, перейти к структуре игроков рынка вкладов представляется весьма нетривиальной задачей. Важный нюанс состоит еще и в том, что почти половина всех вкладов нашей страны принадлежит 1% населения [11]. В силу вышеперечисленных факторов информация по вкладам в России не может отражать действительные накопления каждого слоя общества.

Конечно, для построения ЭСО можно воспользоваться социологическим методом – провести опрос населения. Но опрос зачастую дает искаженную информацию (здесь мы неизбежно столкнемся со сложностью составления репрезентативной выборки – вспомнить хотя бы 1% населения, формирующий половину рынка вкладов), моментную (состояние на день опроса) и является весьма трудоемким.

Метод же математического моделирования ЭСО на основе косвенных данных не только может обеспечить получение результатов, более адекватно отражающих существующие реалии, но и позволит рассчитывать ЭСО при различных значениях параметров модели, а также прослеживать динамику изменения ЭСО и делать прогнозы. Преимущества метода математического моделирования ЭСО трудно переоценить для проведения качественного анализа сложившейся экономической ситуации и возможных сценариев ее развития.

Таким образом, в сложившихся условиях получение достоверных численных оценок ЭСО является востребованной и в то же время непростой экономической задачей.

Отметим также, что сам термин экономической структуры общества (ЭСО) ввел Д.С. Чернавский, который впервые построил математическую модель спектра накоплений общества и исследовал ее поведение при различных управляющих воздействиях [3, 12–13]. Далее специалистами были поставлены смешанные задачи для денежных и материальных накоплений и рассмотрены вероятностные характери-стики1. Группа ученых также занималась вопросами применения спектральных методов к задачам денежных и материальных накоплений [14–15].

В настоящем исследовании рассмотрим модельную задачу – построим модифицированную модель ЭСО на примере статистических данных по Пермскому краю за 2016 г. Предположим, что экономическая структура общества Пермского края качественно будет повторять структуру Российского общества [4], но количественные оценки будут отражать специфику Пермского края и уровень жиз- ни в нем.

В статистическом ежегодном сборнике Пермского края публикуется распределение населения по общим среднедушевым денежным доходам. В соответствии с действующей методологией (утв. постановлением Госкомстата России от 16 июля 1996 г. № 61) общий объем денежных до- ходов определяется на основе суммы от- дельных компонентов: учитываются данные об объемах начисленной заработной платы и выплатах социального характера наемным работникам, доходов от предпринимательской деятельности и собственности, социальных выплат (в виде пенсий, пособий, стипендий и иных мер социальной поддержки), формируемых на основе данных официальной статистической отчетности организаций, осуществляющих выплаты населению1. Учитывая этот факт, упростим модель: будем отталкиваться от общего среднедушевого денежного дохода, не дифференцируя его по видам.

Приведем описание модифицированной в [16] математической модели ЭСО с учетом вышеизложенных допущений.

Модифицированная математическая модель ЭСО Д.С. Чернавского

Д

инамическая модель семейного баланса описывается обыкновенным дифференциальным уравнением dx = P (x, t)- R (x, t),

где x – сумма накопленных денег в семье (отрицательное значение функции x ( t ) будем интерпретировать как долг), P ( x , t ) — доходы семьи, Г [ _P ] = руб ^ , r ( x , t ) — расходы V     мес )

семьи ( y_R] ₌ руб ^ . Последние представимы в V     мес)

виде суммы 4 видов:

R = R + R ₂ + R ₃ + R ₄.                    (2)

Жизненно необходимые повседевные расходы R определяются выражением

R ( x ) = C^- ,                         ⁽³⁾

x + x₀

где C – прожиточный минимум; x – величина накоплений, обеспечивающая по-лублагополучное существование. Повседневные расходы R , обеспечивающие благополучие семьи, задаются формулой R ₂ ( x ) = Bx ® ( x , x₁ ) ,                         (4)

где B – предельная максимально допустимая доля R в общем объеме накоплений; x – примерный уровень накоплений, при котором семья может позволить себе осуществление R2; ®(x, x3) - логистиче ская кривая, определяющая возможность осуществления R . В модели используется

®^{( x} , x ) =T xx                         (5)

Рисковые расходы R представимы в виде R ₃ ( x ) = Ax © ( x , x ₂) ,                           (6)

где A – склонность к предпринимательской деятельности, x – минимальный уровень накоплений для возможного осуществления R . Расходы на уплату налогов R качественно описываются как R ₄ ( x ) = kP & ( P , C ) ,                       (7)

где k – коэффициент предельного налогообложения, P ^~ – налогооблагаемый доход: P = P - R ₃.                                 (8)

Для математического описания того факта, что в реальности семья, помимо гарантированных, может иметь случайные доходы и расходы (выигрыш в лотерею, расходы в связи с болезнью), добавим выражение gZ ( t ) в правую часть уравнения накоплений (1), означающее общее количество денег, которое семья к моменту времени t накопит из случайных источников. z ( t ) — случайная функция, распределенная согласно нормальному закону со средним значением 0 и дисперсией, равной 1; g – амплитуда шума.

С учетом структуры расходов (2)– (8) и случайных факторов уравнение (1)

P = P - Ax ^ ( x , x ₂) .                        (10)

Перейдем к безразмерной форме уравнения (9) с помощью преобразований x * = x / x ,   t * = t / 1 ₀   (время   1 0 = x ₀/ C   харак^-

фициентов сноса и диффузии соответственно. Первый характеризует среднее значение локальной скорости, а второй –

локальную скорость изменения дисперсии приращения марковского процесса [18].

Определив все коэффициенты модели, перейдем к ее непосредственному

численному расчету.

терно для оборота денег в семье) и сохраним для удобства старые обозначения переменных и коэффициентов. Таким образом, получим модифицированное динамическое уравнение типологии семейных накоплений в безразмерной форме:

dx = ( 1 - Ц P ,1 )) P x - Bx 0 ( x , x 1 ) + g Z ( t ) , ⁽¹¹⁾ ~ = P - Ax e ( x , x ). ⁺                    (12)

Перепишем (11) в характерном для уравнений Ланжевена виде, выделяя в правой части детерминированную и случайную компоненты:

dx = F ( x ) + G ( x , Z ) ,                           ⁽¹³⁾

^где F ( x ) = ( 1 - k o ( P,1 ) P--x^ - Bx 0 (x , x ) ,

G ( x , Z ) = g Z ( t ) .                                  ⁽¹⁴⁾

Уравнение (13) – стохастическое дифференциальное уравнение. Марковский процесс первого порядка x(t) полно-

Численная реализация модели

ЭСО на примере статистической вы-

борки по Пермскому краю

С огласно имеющейся статистике по Пермскому краю за 2016 г. выделим четыре эко-

стью определяется плотностью вероятности р ( x , t ) , которая подчиняется уравне-

нию Фоккера – Планка [17]:

др д t

^{д 1} F ^{( x} ) • Р ⁾⁺ д x

g 2 &L 2 дx²

р

Уравнение (15) представляет собой дифференциальное уравнение в частных производных параболического типа. Первоначально уравнения Фоккера – Планка применялись в основном в физике для изучения поведения броуновских частиц.

В нашем случае в качестве элемен-

номические группы по уровню среднедушевого среднемесячного дохода:

• -    бедные (с доходом менее 1,04 прожиточного минимума), их доля в общем объеме населения Пермского края составляет 16,1%;

• -    малообеспеченные (с доходом 1,04–1,98 прожиточных минимумов), их доля в выборке составляет 27,7%;

• -    обеспеченные (с доходом 1,984,69 прожиточных минимумов), их доля составляет 39,5%;

• -    богатые (с доходом 4,69-20 прожиточных минимумов), их доля составляет 16,6%.

По аналогии с [3] и преимущественно методом экспертных оценок определим параметры модели.

Величина накоплений, обеспечивающая полублагополучное существование, составляет x₀ = 9591 руб. (прожиточный минимум по Пермскому краю в 2016 г.). Период кругооборота денег в семье ( t ₀)

тарных частиц выступают семьи, а плотность распределения р ( x , t ) означает долю тех семей в общей выборке, накопления которых находятся в пределах от x до x + A x . Размерность функции плотности распределения Р ] = _L.

руб

За «коэффициентами» F ( x ) и g² исторически закрепились названия коэф-

составляет один месяц.

При достаточных накоплениях семья начинает приобретать товары, которые уже не являются товарами первой необходимости, а относятся к категории элитарных товаров (видеотехника, автомобиль, дача). Минимальный уровень этих накоплений определим как 10 прожиточных минимумов: x = 10 • 9591 = 95910 руб., или, в безразмерном виде, x = 10 . Согласно модели эта величина соответствует цене самого дешевого элитарного товара. За среднюю цену элитарного товара примем

x₂ = 40 . 9591 = 383640 руб. (в безразмерном виде х₂ = 40 ).

Коэффициент предельного налогообложения k задан как 0,35.

Коэффициент A соответствует безрисковым вложениям в Сбербанке. Он равен 0,015.

Параметр B принят равным 0,1. Это означает, что на улучшение своего благополучия люди готовы отдать 10% накоплений.

Коэффициент g , отражающий величину случайных потерь или приобретений, задавался в интервале от 3 до 5,8.

Численное исследование модели проводилось в системе COMSOL Multiphysics 4.2.

Таблица 1

Различающиеся числовые значения параметров задачи для каждой экономической группы

Экономическая группа	ГраницаL2		Начальные условия	Граничные условия
	L1	L2	р ( X ,0 )	р ( L 1, t )	р ( L 2, t )
Бедные	0	31,28	0,161	0,500000	0,000002
Малообеспеченные	0	41,71	0,277	0,400000	0,000069
Обеспеченные	0	62,56	0,395	0,150000	0,000096
Богатые	0	135,54	0,166	0,000572	0,001143

ЭСО Пермского края, как и любого региона России, в условиях рыночной экономики формировалась с 1990-х гг., поэтому для 2016 г. примем ее стационарной.

Приведем результаты численного моделирования.

На рис. 1–4 приведены графики функции плотности распределения населения р для каждой выделенной экономической группы. Видно, что с увеличением дохода, максимум накоплений движется вправо. Этот результат не вызывает сомнений: более обеспеченные слои населения имеют больше возможностей сберегать свои средства, так как на удовлетворение жизненно необходимых потребностей уходит малая доля их дохода.

Для кластера бедных семей характерен стационарный уровень накоплений в 2,37 прожиточных минимумов (рис. 1), для кластера малообеспеченных семей – 8,22 прожиточных минимумов (рис. 2), класте-

Для каждой экономической группы решалась задача на промежутке [L1;L2] (табл. 1). В качестве начального условия было взято известное из официальной статистики распределение населения по среднедушевым доходам (было сделано допущение об отсутствии расходов в начальный момент времени). Граничные условия задавались экспертными оценками, исходя из данных ВЦИОМ: в 2016 г. 39% респондентов сообщили, что у них нет накоплений1). В табл. 1 приведем использованные для расчета модели значения параметров задачи, различающиеся в зависимости от экономической группы.

ра обеспеченных семей – 13,76 прожиточных минимумов (рис. 3) и, наконец, кластера богатых – 64,21 прожиточных минимумов (рис. 4).

Под1 стационарным уровнем накоплений, по сути, подразумевается наиболее вероятный уровень накоплений в каждой экономической группе. В процессе установления стационарного состояния в своей группе одни семьи могут больше других тратить, другие – больше экономить, однако так или иначе они в итоге приходят к единому уровню накоплений в своем кластере. Таким образом, сложившаяся экономическая среда как бы подталкивает людей одного кластера скапливаться в районе примерно одинакового уровня накоплений.

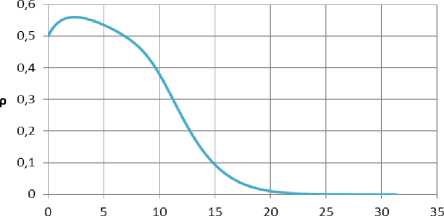
х, накопления (ПМ)

Рис. 1. Стационарное распределение по накоплениям для кластера бедных семей

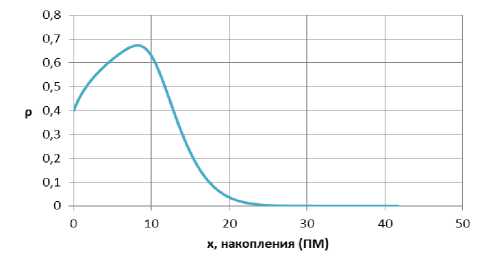
Рис. 2. Стационарное распределение по накоплениям для кластера малообеспеченных семей

Интерес представляет также общее стационарное распределение накоплений для всего населения Пермского края. Чтобы его получить, просуммируем значения функций плотностей распределения с весовыми коэффициентами, соответствующими доле каждой экономической группы в общей выборочной совокупности. Полученное суммарное стационарное распределение накоплений приведено на рис. 5. По графику видно, что функция суммарного стационарного распределения накоплений имеет два максимума: при x = 10.3 и x = 63.5 прожиточных минимумов.

Прежде всего отметим, что ЭСО Пермского края бимодальна, т.е. имеет два максимума. Такая особенность распределения присуща России в целом и унаследована со времен СССР [3].

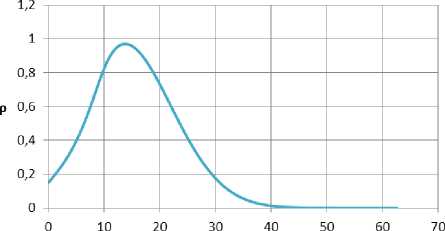
х, накопления (ПМ)

Рис. 3. Стационарное распределение по накоплениям для кластера обеспеченных семей

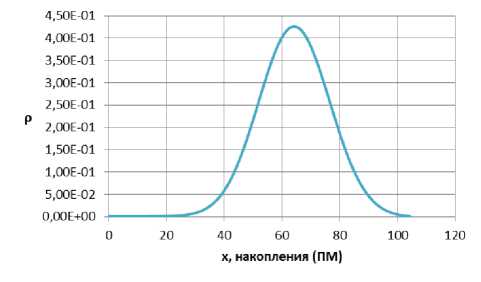
Рис. 4. Стационарное распределение по накоплениям для кластера богатых семей

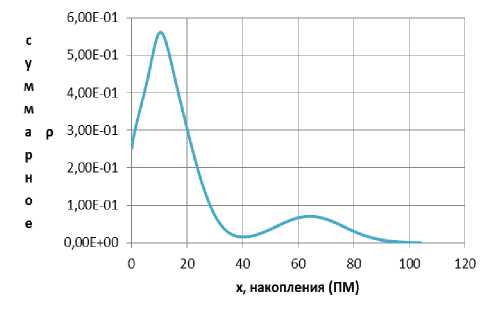
Рис. 5. Суммарное стационарное распределение по накоплениям для всего населения

В развитых странах эта структура унимодальна, и горб соответствует среднему классу общества (рис. 6).

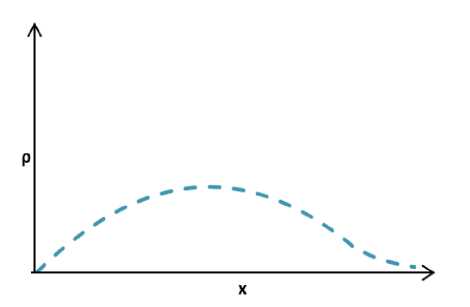
Рис. 6. Распределение по ликвидным накоплениям в Японии [4]

Таким образом, можно утверждать, что в обществе Пермского края средний класс практически отсутствует и все общество условно делится на две неравные группы. Первую группу составляет 83,4% населения Пермского края, и им принадлежит примерно 40% всех накоплений. Ко второй группе, «элите», можно отнести 16,6% населения, которые обладают 60% всех накоплений. По графику также видно, что эти экономические группы достаточно раздвинуты по оси накоплений, так что аргументы максимумов отличаются примерно в 6,15 раза. Эти цифры также говорят о высокой концентрации сбережений у малочисленной «богатой» части общества.

Отметим для сравнения, что в СССР до реформ (1987 г.) 85% всего населения владели 20% всех накоплений, а на долю оставшихся 15% приходилось 80% всех накоплений, и отношение аргументов максимумов составляло 70 [3]. Возможно, разрыв в накоплениях бедной и богатой групп общества был намного существеннее, поскольку под «богатыми» понималась самая верхушка общества СССР. Мы же в своем исследовании ограничились рассмотрением «богатых», чей доход не превышал 20 прожиточных минимумов, и отсекли самые верхние слои, по величине доходов которых у нас нет достоверной информации. Рассуждая дальше, можно предположить, что горб «бедных», существовавший в СССР, в нашем обществе разделился на 2 горба, и в состав второго горба «богатых» входят топ-менеджмент и активные предприниматели, которые смогли в условиях рыночной экономики преумножить свои сбережения.

В целом полученное распределение по накоплениям вполне соответствует распределению по доходам, публикуемом ежегодно в официальных источниках, согласно которому 20% населения с максимальными доходами распределяют между собой 47,1% всех доходов общества Пермского края, и более наглядно демонстрирует факт расслоения общества на «богатых» и «бедных».

Заключение

В работе была численно исследована математическая модель экономической структуры общества Пермского края. Полученные результаты говорят о ее бимодальности. Наиболее вероятные уровни накоплений жителей Пермского края составляют примерно 10 и 63 прожиточных минимумов.

В таких случаях, когда ЭСО существенно отличается по своей структуре от нормального распределения, заменять ее средним значением в различных экономических расчетах с математической точки зрения является недопустимым, поскольку это приводит к получению заведомо некорректных результатов. Кроме того, в периоды экономических кризисов распределение по накоплениям является нестацио- нарным и может значительно отличаться от докризисной устоявшейся структуры.

В силу этих обстоятельств, а также учитывая условия дефицита достоверной информации о спектре накоплений общества, его математическое моделирование может быть очень востребованным.

Отметим, что в целом последние несколько десятков лет математическое моделирование социально-экономических процессов с учетом их стохастических составляющих бурно и успешно развивается во всем мире и нашей стране [19–23]. Возможность применения математического аппарата к таким сложным явлениям связана с простой закономерностью, вытекающей из закона больших чисел: непредсказуемость поведения отдельных элементов (в нашем случае семей) больше, чем их однородной группы, и, наоборот, она уменьшается по мере роста численности этой однородной совокупности.

Анализ ЭСО может быть интересен государственным структурам и различным организациям, предоставляющим финансовые услуги населению, для выработки обоснованных управленческих решений в области накоплений населения, в оценке уровня жизни и других экономических переменных. Отметим, что перспективным направлением развития математического моделирования ЭСО, которое может при- нести еще большую практическую значимость, является исследование задач оптимального управления спектром накопле- ний общества [24] с помощью методологии, описанной в исследовании А.В. Фур-сикова [25].