Математическое моделирование экосистемы озера Байкал: вчера, сегодня, завтра

,.

.                   .-

.                  ,-

.-

,                                      ,-

,-

,-

..

,                                                                                                    ,-

.

Экосистема озера Байкал стала одним из

-

-

.

-

.

..               , . .                 ..-

[1, 2].-

: «                                    », «-

», «                », «-

», «       », «       » «».

использовался диапазон изменений каждой 0 +1, 0« -

», +1 «-

»,               «           »,,

0,5,

,        «-

»                          0, «-

»

• 1,    «»

+1.

«»

6:

• -              ,         -           ,            -, -

• -         ,         -       ,--
• .-

  -

• ,-
• ,              ,-
• ,

,-

,

• -,     ,,

.- трация биогенных элементов определяется

,-

.- речисленных факторов происходят сезонные

,-

,, -

,

,

.

Остальные подмодели не имеют сезонной

.«»

«-

»-

,«-

», «                 », «»

«Омуль» среднегодовыми количествами рыб, поедающих рачка.

Для подмоделей рыб среднегодовое коли -чество макрогектопуса служит положитель-но действующим фактором, а для планктона - отрицательным. СС убмодели рыб имеют возрастные группы: по 3 - у длиннокрылки и желтокрылки, 6 с у голомянки и 10 су омуля. Каждая из них зависит от планктона и мак -рогектопуса, смуль - еще и от бентоса. Омуль и желтокрылка вылавливаются, причем вылов регулируется величиной промыслового усилия.

X ( t ) = Ax ( t ) + Bx ( t -1) + Cu ( t ), где

u ( t ) = ( u i( t ),..., u ₂o( t )), u ( t ) e [0,1] x ( t ) = ( x 1( t ),..

Желтокрылка, ссиннокрылка и голомянка поставляют пищу нерпе, соличество которой сказывается на них и определяется промыс-лом, который зависит от промыслового усилия . Наконец бентос зависит от температурных и кормовых условий через планктонный блок и от выедания омулем.

Всего в модели 120 переменных состояния , можно варьировать 20 сходных переменных , 3 пессменных - полезный выход в виде вылова желтокрылки и омуля, добычи нерпы .

Модель представлена системой линейных уравнений:

- вектор входных переменных для года t ,

, x ₁₂₀( t )), x, ( t ) e [0,1] - вектор фазовых переменных в тот же год,

A - матрица коэффициентов влияния внутри года,

B - матрица межгодовых связей,

C - матрица зависимости переменных модели от внешних условий.

При этом:

120                  20

£( « ДМ)+ Е С «1 = 1, ‘ =1,2,...,120.

j =1                      к =1

У стандартной точки системы все коорди-наты равны 0,5.

Эта модель самими авторами расценива-лась как промежуточный этап в работе и по -зволяла получать только качественные резуль -таты. Тсм не менее ее исследование позволило найти ряд зависимостей между абиоти-ческими факторами, обнаружить, сто биотические компоненты мало зависят от темпе -ратуры воздуха, но сильно зависят от инсоляции и ветровых условий, сыделить наиболее чувствительные к солнечной радиации (фитопланктон, бактерии, коловратки, циклоп ) и ветровой активности (фитопланктон) элементы сообщества. Ряд положений исходно полученных в экспериментах с моделью сейчас подтвержден анализом данных поле -вых наблюдений [9].

Следующей стала энергетическая модель пелагического сообщества оз. Байкал Л.Я. Ащепковой, В.И. Гурмана и О.М. Кожовой [1]. Модель, как и предыдущая, точечная. В модели рассматривались потоки энергии в слое

0-250 м.

В модель включены следующие компонен-сы: фитопланктон ( x 1), спишура ( x ₂), циклоп ( x ₃), макрогектопус ( x 4), смуль ( x ₅), пелагические бычки ( x ₆), соломянка ( x ₇), серпа ( x 8), бактерии ( x ₉), детрит ( x ₁₀). В модели приняты следующие обозначения:

b . - биомасса z'-со компонента, г. - поток энергии от z-ro компонента к j-му, q . - энергетический обмен компонента i, m - потери энергии со смертью i-со компонента , u . - неусвоенные остатки пищи компонен-с a i,

К. - напряженность трофических отноше-ний компонента i, j - для z-ro компонент а в питании j-го, cjmax - удельный максимальный рацион, A - годовой приток аллохтонной органики ,

S 1 - седиментация органики,

S ₂- сток органики через Ангару.

Потоки энергии , функции биомасс вычислялись по формуле Меншуткина,- лева и Вольтера не дали желательной устой-:

j1e ii ri j(bi,bj) cmjaxbjА ij i , j max j ij, кi cmj axbjxij cmax (bi ) = а je jbj.

Средняя поправка Меншуткина ( формуле для r _ij ( b _i , b _j ))

0,8.                        v V- ловия,          bj->0,- ный рацион увеличивается в 2- нению с максимальным рационом для сред-него значения биомассы .

энергии со смертью линейно зависели от био-масс компонентов,- оны,- циона.

:

db

• ¹    r 01 q 1 m 1 "Е r 1 j , dt j

• ^d d^bt ⁱ -=Е r ij q _i m _i u _i -Е r ij , i 2,3,...,9,

• ^d d^bt ¹⁰ -=Е m _i +Е u_i + r 109 + A S 1 S 2 , dt i i

где S1 = kb10, S2 = mb10. k значение 6,7, m - 20.

омуля и нерпы были введены потоки r50 r80, означающие их добычу и связанные с соот-ветствующими биомассами линейно .     - рименты с полученной моделью показали связь первичной продукции экосистемы с притоком аллохтонной органики .

была подчеркнута гипотетичность применен-ных в модели коэффициентов и необходи-мость их уточнения в полевых эксперимен-тах на озере.

Сохранив те же функции для имитации биологических процессов В .В.

соавторами [15]- дель озера,- та на 65              484   2,- ная толща была разбита на трофогенную (05 0 ).

модель неплохо отражала реальную динами-ку экосистемы, распространения попавшего в озеро веще-ства, экосистемы в одной точке на другие районы.

Затем вот уже 20 ни одной попытки построения имитацион-ной модели естественной динамики экосис-темы озера.                    ,             - рование естественной динамики экосистем промежуточного ( океаном)                          ,     [3, 14]:

• -    существуют факторы,               -

• ном на динамику не влияют,             -
• ,

• -    для каждой фазы динамики определяю-щими являются свои собственные факторы,

• -    характер и уровень связей для различ-ных фаз существенно различаются,

• -    многие закономерности со временем раз-рушаются.

Если мы рассмотрим естественную дина-мику компонентов экосистемы пелагиали оз. Байкал ,            , всех компонентов непрерывно колеблются [17].   -видимому, колебаний зависят не только от внутренних механизмов взаимодействия компонентов, и от внешних факторов,               (на- пример,                     ),               - генных [5].

В связи с необходимостью оценки послед-

-тему было решено ограничиться построени-

-системы озера., что естественная динамика рассматривается как некая прямая («нулевое»), -

(увеличение) или отрицательным (уменьшение) [18-20, 22].

В первую очередь надо было выбрать ком-поненты,- дель .- ных моделей из биологических компонентов были взяты фито-, зоо- и бактериопланктон. Гидрохимические компоненты были пред -ставлены в модели суммарной минерализа-цией вод, концентрациями биогенных элементов (нитратный азот и фосфатный фосфор ), растворенное органическое вещество (измеряемое как ХПК). Кроме того, учтены главные токсичные вещества, попадающие в озеро, главным образом в результате хозяйственной деятельности: нефтепродукты, фенольные соединения, ионы тяжелых металлов .

В качестве исходной модели рассматрива-лась следующая:

dR / dt = Q ( R-R *) + u + r , (1)

где R - вектор состояния экосистемы (биомассы и концентрации компонентов),

R* - лектор невозмущенного состояния экосистемы (сллднее за много лет значение этого компонента для данного времени года), и - вектор внешних воздействий (поступление загрязнений ), r - вектор переноса компонентов (миграции , перенос течениями и диффузия между ячейками ),

Q - матрица взаимовлияний компонентов экосистемы (каждый элемент qj показывает изменения компонента i в единицу времени при отклонении компонентаj ла единицу, диагональные элементы qu отражают динамику возвращения i-го компонента в исходное состояние после отклонения, это скорости самовосстановления биологических компо- dZ't /d \»Z +(1/Vt)£{P.Z; j=1                          l^L

где L - агрегат соседних камер, P , D л матрицы турбулентности и диффузии, рассчитанные Е.А. Цветовой, V лл вектор объемов камер .

При моделировании наиболее сложной и трудоемкой является задача информационно -го обеспечения. Основываясь на опыте построения моделей О.М. Кожовой, ле было решено провести на основе натурных экспе-риментов, лаправленных на определение неизвестных параметров. Для этого была применена следующая технология.

нентов и константы скоростей распада заг-рязнителей ).

Была принята следующая схема разбиения водного тела на камеры (см. рис. 1). По глубине было выделено уже не два, а с учетом опыта работы с моделью В .В. Меншуткина и др. [15], три слоя, различающихся по физическим и биологическим показателям:

• •    0-50 м (трофогенный, лорошо освещенный слой со значительными годовыми перепа-дами температур, фито-, зоо-, бактериопланктон ),

• •    50-250 м (очень слабо освещенный слой, перемешивание, течения, меньшие перепады температур, зоо- и бактериопланктон),

• •    250 м - дно (постоянные температурные условия, полная темнота, бактериопланктон ). По горизонтали 2 верхних слоя были разделены на 10 камер каждый, нижний слой рассматривался как одна камера.

Использование вектора некоего невозму-щенного состояния экосистемы предполага-ет, что мы знаем это невозмущенное состояние . Поскольку это не так, модель (1) была заменена моделью, выраженной в терминах отклонений [22]:

N dZj/ dt^QyZ^Ui,           (2)

j =1

где Z л вектор отклонений показателей состояния , N лл число показателей, U лл вектор управления .

С учетом гидрологического блока мы по -лучаем:

• -P k Z' .+ D ki ( Z l- Z k )}] U k , (3)

Пусть объект описывается следующей ма-тематической моделью:

dZ / dt = f ( t , z , a )                (4)

При наличии m реализаций и наблюдаемости части компонент:

Z j ( t ) = ( Z ^lj ( t ),..., Z^mjt t )),        ^{j = 1} m

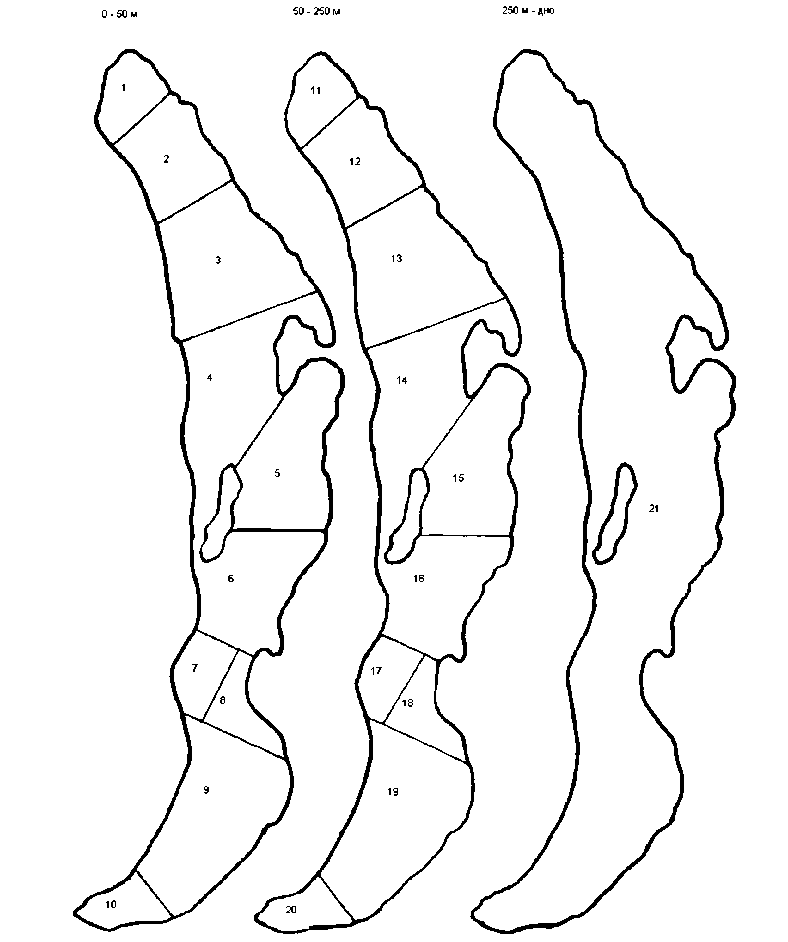
. 1.                                                                                               .                                             ,

При задании m начальных условий:

Z i tt ₀) = Z 0,                        i = 1, m .

надо минимизировать функционал t ^fm                             m

• I= ВЁ 'LL Z Z j) ) ² dt+L^jt^ t k )- Z ^j ( t k »2 > (5) t ₀ i =1 ) j                         i =1 ) mMj

где i - номер компонента вектора Z, j - номер испытания,

M j - множество номеров компонент вектора Z , наблюдаемых в ) -м испытании,

Рi., у*. - aaniaua eiyooeoeafou.

На основе экспериментального материа-ла [6-8] определялись величины отклонений z _в на каждый учитываемый момент времени и коэффициенты системы:

z ‘^^ч ,          ' , к =ш  (6)

где первоначальные коэффициенты q , определялись экспертной оценкой, a, b g g принимались равными 1. После минимизации функционала и определения новых q _& система вновь интегрировалась, полученные значения z сравнивались с экспериментальными . Пр и наличии существенных расхождений процесс повторялся с новыми b и д .

Таким образом, для определения коэффициентов взаимовлияния для модели из N компонентов было необходимо поставить N серий опытов, в каждой из которых отклоняя на заданную величину один из компонентов, а затем определяя концентрации всех компо-нентов до конца экспозиции. В нашем случае вносились следующие отклонения:

• •    добавки сульфата натрия (повышение минерализации ),

• •    добавки нитратного азота и фосфатного фосфора,

• •    добавки аллохтонной органики (пептон)

• •    добавки фенольных соединений (пирокатехина ),

• •    добавки нефтепродуктов (водная эмульсия

дизельного топлива),

• •    добавки ионов тяжелых металлов (хлорид кадмия ),

• •    бактериопланктона,

• •    фитопланктона и

• •   зоопланктона.

Два последних концентрировались с по -мощью соответствующих планктонных сетей и вносились в экспериментальные мезокос-мы (объемом 2 м3) непосредственно из озера .

Использование алгоритмов, разработанных и реализованных в виде программного комплекса в ИрВЦ ВСФ СО РАН, позволило решить поставленные задачи. На основе данных , волученных в натурных экспериментах на оз. Байкал, Ввши рассчитаны матрицы взаимовлияния компонентов для подледного и летне - осеннего сезонов.

После определения компонентов матрицы Q, в первую очередь был проведен анализ устойчивости модели. Она оказалась внутренне устойчива.

Сценарии модельных экспериментов вы -бирались на основе доступных опубликован -ных данных. Для современного уровня хозяйственной активности были приняты следу -ющие величины поступления химических веществ в озеро (см. табл. 1).

Сначала были проведены эксперименты

1.                                                                       (         -1)

хозяйственной деятельности

Вещество С водами притоков С атмосферными осадками и     Со сточными водами БЦБК смывом с берегов Сульфаты Нитраты Фосфаты Органическое вещество Фенольные соединения Нефтепродукты Ионы кадмия 200 103                                                         26 103 23                         6 0,5                            2 160 103                                                             8103 160                        40                               2 10,2 103                        3,2 103 1,5                              -                                     0,3 для односезонных (период открытой воды и подледный) точечных моделей (без учета гидрологии ) в шагом в один день.

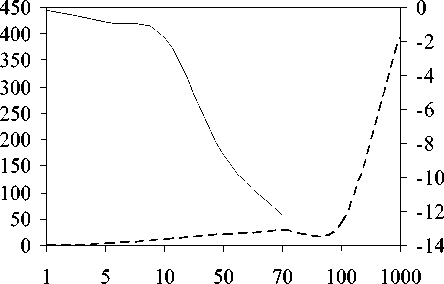
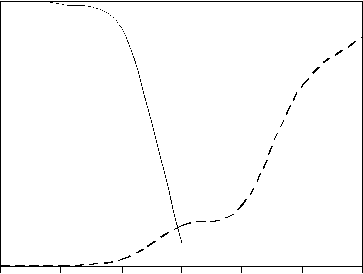
Были проанализированы ответы модели на токсификацию и эвтрофирование. Сравнивались воздействие разового стартового внесения токсикантов и биогенных веществ и их хронического действия. Подледное сообщество оказалось значительно чувствитель-нее летнего и к токсификации, и к эвтрофи-р вванию (рис. 2) и медленнее возвращалось к исходному состоянию, чем летнее (табл. 2

-5

-10

-15

-20

-25

1     10 100 900 1000 3000 3800

Рис. 2. Действие (А) смеси нитрата и фосфата натрия ([4N+1P] мкг Л" )и(Б) фенольных соединений на общую биомассу планктона (мкг л^-1) подо льдом (правая шкала) и летом (левая шкала, пунктир)

Таблица 2. Максимальное отклонение компонентов (мкг Л"1) в ответ на разовое поступление фенольных соединений (100 мкг Л"¹)

Компоненты	Подледное сообщество		Летнее сообщество
	от	до	от	до
Биогены	-1.52	0.46	-1.80	0.25
Фитопланктон	-4.12	1.21	-1.19	2.68
Зоопланктон	-1.11	1.85	-0.51	0.48
Возвращение к исходному состоянию через (сут .)	34		23

Таблица 3. Максимальное отклонение компонентов (мкг Л"1) в ответ на разовое поступление биогенных соединений (10 мкгР Л"¹и 40 мкгN Л"¹)

Компоненты	Подледное сообщество		Летнее сообщество
	от	до	от	до
Фенолы	0.00	1.39	0.00	2.95
Фитопланктон	-23.63	8.61	-6.69	24.63
Зоопланктон	-9.95	21.69	-1.55	3.68
Возвращение к исходному состоянию через (сут .)	36		24

Таблица 4. Отклонение компонентов (мкг Л"1) в ответ на хроническое поступление фенольных соединений (100 мкг Л"¹ сут. ¹)

Компоненты Подледное сообщество Летнее сообщество Биогены -1.56 -1.29 Фенолы 98.27 68.45 Фитопланктон -3.16 1.07 Зоопланктон 0.63 -0.16 Переходит в новое стационарное состояние через (сут .) 45 34 и 3). Оно также медленнее переходило в но-вое стационарное состояние, чем летнее при хроническом поступлении загрязнений (табл . 4и 5). На рис . 3и4 приведены результаты моделирования при поступлении всех загряз- нителей в летне-осенний (все пути поступ-ления загрязнителей) и зимне-весенний (по-ступление с водами притоков) периоды . Очень заметна меньшая устойчивость сооб-щества в подледный период, особенно при

Таблица 5. Отклонение компонентов (мкг Л"1) в ответ на хроническое поступление биогенных соединений (10 мкгР Л"¹и 40 мкгN Л"¹ сут. ¹)

Компоненты	Подледное сообщество	Летнее сообщество
Биогены	38.07	42.10
Фенолы	0.00	1.81
Фитопланктон	-20.30	17.34
Зоопланктон	11.57	2.26
Переходит в новое стационарное состояние через (сут.)	43	29

Б

А

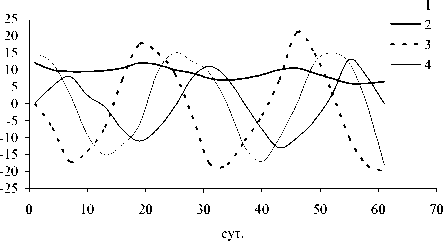
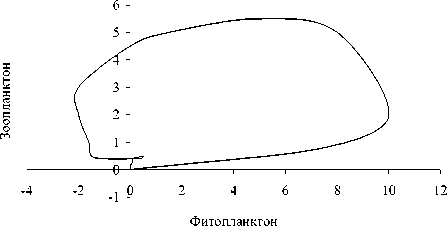
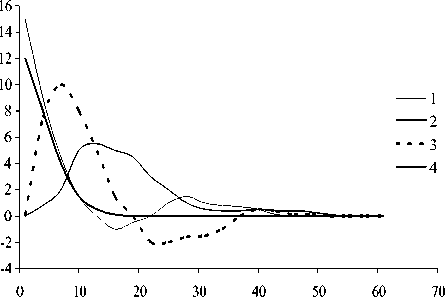
Рис. 3. Динамика отклонений (мкг л -1) ряда показателей состояния экосистемы в летне-осенний период (А) и фазовый портрет системы (Б): 1 - суммарная концентрация нитратного азота и фосфатного фосфора , 2 - концентрация фенольных соединений, 3 - концентрация фитопланктона, 4 - концентрация зоопланктона

Б

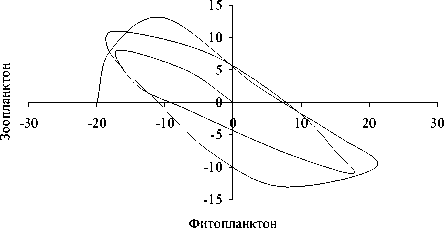
Рис. 4. Динамика отклонений (мкг л-1) ряда показателей состояния экосистемы в зимне-весенний период (А) и фазовый портрет системы (Б): 1 - суммарная концентрация нитратного азота и фосфатного фосфора, 2 - концентрация фенольных соединений, 3 - концентрация фитопланктона, 4 - концентрация зоопланктона

обращении к фазовым портретам (рис . 3Б и 4Б). Видно, что система стремится к асимп-тотической устойчивости в летний период и демонстрирует орбитальную неустойчивость в подледный период. Это еще раз подтверж-дает высказанное выше предположение о большей чувствительности подледного план-ктонного комплекса к возмущающим воздей- ствиям.

Надо отметить, что полученные на мате-матических моделях результаты реалистично отражают процессы, наблюдавшиеся в мезо-космах, как в ходе наших полевых экспери-ментов, так и отмечавшиеся для оз. Байкал другой группой исследователей [10]. В натур-ных экспериментах с мезокосмами на озере

A

-10

-20

0      5      10     15     20     25     30     35     40

.

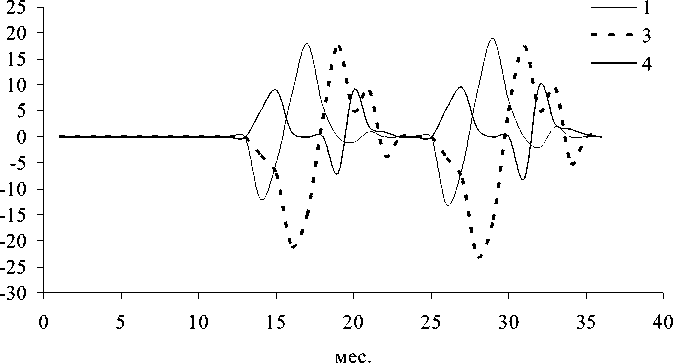
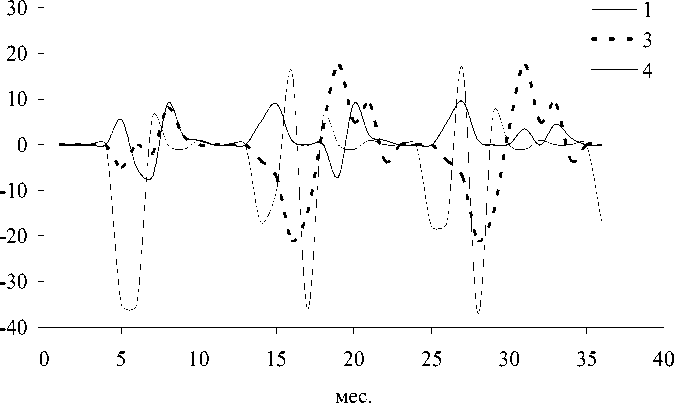
Рис. 5. Динамика отклонений (мкг л^-1) ряд а показателей состояния в поверхностном слое при поступлении загрязнителей с атмосферными осадками (А); пр идонном слое при поступлении загрязнителей с атмосферными осадками (Б); поверхностном слое (Северный Байкал) пр и поступлении загрязнителей с водами р. Селенги (В): 1 -суммарная концентрация нитратного азота и фосфатного фосфора, 3 - концентрация фитопланктона, 4 - концентрация зоопланктона, 5 - концентрация бактериопланктона

Байкал показана большая чувствительность

,-

,

,-

(

),                                              .,

,-

(

-

),-

.

,-

-

,-

.

-

-

• [ 23].      ,-

  -

• лучаем следующую картину в поверхностном

• (    . 5 ).,

  -

  -

• )    (     . 5 ).-

  -

• .-
• вания начинают отмечаться отклонения от

  -

• (    . 5 ). -

  -

• ,-
• ,-

  -

• (    . . 6 ).             ,-
• .-
• ,-
• ,

( . 6 ).

,,

, подтверждение при анализе трендов ряда гидрохимических показателей по материалам наблюдений Государственного комитета по

,              -

.                            , -

-

[12, 13].

Модель возмущений явилась логичной наследницей первых моделей экосистемы

.                                                                          -

,                      -

, - ет разбиение водной толщи на камеры по

-

.                                   ,-

,«-

». -

.-

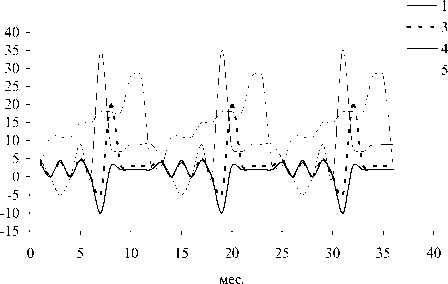
Б

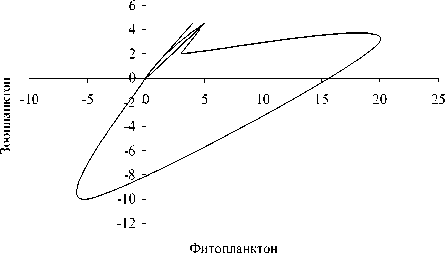
Рис. 6. Динамика отклонений (мкг л-1) ряд а показателей состояния в поверхностном слое при поступлении загрязнителей с водами притоков, атмосферными осадками, при таянии льда (А) и фазовый портрет системы (Б): 1 - суммарная концентрация нитратного азота и фосфатного фосфора, 3 - концентрация фитопланктона, 4 - концентрация зоопланктона, 5 - концентрация бактериопланктона тивно начинают использоваться модели структурной динамики, в частности на осно-ве целевых функций, таких как эксэргия [4, 20], ведется работа по разработке самоорга-