Математическое моделирование электрических полей в электрофизических установках

Из множества электрофизических установок ограничимся рассмотрением только импульсных ускорителей электронов [1], используемых для рентгенографии с целью экспериментального измерения характеристик поведения исследуемых веществ под действием динамических нагрузок. Разрешающая способность таких установок прямо зависит от напряжения электрического поля. При его увеличении увеличивается глубина просвечивания образцов и контрастность получаемых изображений, но одновременно возрастает опасность разрушения установки. Иными словами, реализуемая величина напряжения зависит от взаимодействия нескольких взаимосвязанных конкурирующих процессов: разрядка конденсаторов, транспорт энергии, пробой изоляторов.

Каждая физическая модель описывает реальные физические процессы с погрешностью А фИЗ . Погрешность математического моделирования складывается из погрешности физической модели и погрешности численного решения А = А физ + А мат .Что6ы иметь возможность сравнения физических моделей и выбора модели с минимальным значением А физ , необходимо, чтобы было А мат ^ А физ . Особенно это важно, когда речь заходит о моделировании сложных, многофакторных и разномасштабных явлений. Из публикаций [2–5] известно, что наилучшими свойствами с точки зрения выполнения законов сохранения и сходимости обладают разностные схемы, полученные путем интегрирования основных уравнений по объему или по поверхности ячейки и применении теоремы о среднем значении, и использующие адаптивные разностные сетки. Среди методов построения адаптивных сеток наиболее простым является метод, использующий ячейки только одной формы, а размеры соседних ячеек могут отличатся в два раза и более, так что неизбежно возникает необходимость контроля точности получаемых приближенных решений. Для этого проводятся как теоретические оценки погрешности аппроксимации и устойчивости разностных уравнений, так и расчетные исследования сходимости результатов применения метода на модельных задачах, близких к реальным.

1.    Разностный оператор Лапласа

B электростатике уравнения Максвелла для электрического поля принимают вид уравнений Пуассона или Гельмгольца [6]. И в том, и в другом уравнении центральное место занимает оператор Лапласа. В данной работе рассматривается оператор Лапласа в двумерной цилиндрической (r, z) геометрии l.=r£ irdt)+д (g). (i)

где .(r, z) — электрический потенциал. Покроем расчетную область ячейками одинаковой (квадратной) формы: отношение длины стороны базовой ячейки к длине стороны любой ячейки равно целой степени числа 2. Таким образом, каждая ячейка по каждой из своих четырех границ граничит с одной или с несколькими соседними ячейками (рис. 1).

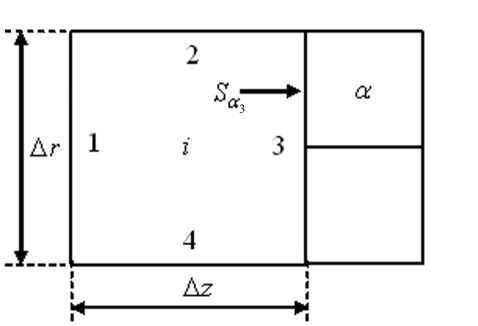
Рис. 1 . Нумерация в ячейке расчетной области на примере ячейки, имеющей два соседа по третьей стороне

Искомую функцию ϕ определим в центрах ячеек. Для получения разностных соотношений интегро-интерполяционным методом [7] умножим (1) на элемент объема dV = 2 nrdrdz, и проинтегрируем по объему ячейки V

[\ 1 122 + 22 ]2 nrdrdz-              (2)

r∂r ∂r ∂z ∂z

Применив теорему Остроградского–Гаусса, запишем (2) в виде

(j) 22 2nrdz +

∂r

(I) 22 2nrdr.

∂z

Заменив с помощью теоремы о среднем значении поверхностный интеграл на каждой грани сеточной ячейки средним значением подынтегральной функции, получим на адаптивновстраиваемой сетке разностный оператор Лапласа

• л. = EE ^ i k z-? S a k + EE .j^ S a k ,          (4)

k=1,3 αk i             k=2,4 αk       i где i – номер ячейки, k – номер стороны ячейки, αk – номер соседней ячейки по k-й стороне, ϕ∗αk – значения потенциала на границах ячейки, а Sαk – площадь границы двух ячеек (по сторонам 1 и 3: Sak = 2nrak Arak, по стороне 2: Sak = 2п (г. + Ari/2)Arak, по стороне 4: Sak = 2п (ri — Ari/2) Arak. Вспомогательные величины у* определяются линейной интерполяцией по значениям функции-потенциала в двух соответствующих ячейках (i и αk ) соответственно для соседей по вертикали (к = 1, 3)

* = V a _k Az i + V i AZ a k ^Va k      Az j + A Z a _k

или по горизонтали ( к = 2 , 4)

* = V a _k Ar j + V i Ar a k ^Va k       Ar i + Ar a _k '

Площадь границы между соседними ячейками по сторонам 1 и 3 S _a 1 3 (см. рис. 1) и по сторонам 2 и 4 S _a 2 4 определяются выражениями

S a i,3 = 2 nr a i,3 A r a i,3 , S a 2,4 = 2 n ( r + ^A r^A^^.                    (7)

Подставляя значение выражений вспомогательных величин (5), (6) и значения площадей граней ячеек сетки (7) в (4), а также, учитывая квадратность ячеек (A r i = Az . = h i ), получаем следующий вид разностного оператора Лапласа:

Л у

ЕЕ

k=1,3 a k

2hak (yak   yi) 1 rak hi + hak    h2 ri

+ k=2,4 ak

^2h a k ^(v a k    ^y i ) ¹

h i + h a _k     h ²

(^{1+(3 — k )}2r9 •

Разлагая входящие в (8) сеточные значения функции ϕ в ряды Тэйлора в центре сеточной ячейки, получим уравнение

Лу = Ly + Ry, где R зависит от количества соседних ячеек и имеет вид

R ⁽ n, ^{m )} = ( dzy ^ i ⁽ A n ⁺ A m ) ⁺ ( dry ) . ^{( B +} B m ) ⁺ r i ( dr ) i ⁽ C n ⁺ C m ) ⁺ ^ ^{( h )} "  ⁽¹⁰⁾

Коэффициенты A _n , B _n , C _n зависят от n (число соседей слева и справа), коэффициенты A _m , B _m , C _m зависят от m (число соседей сверху и снизу). Значения этих коэффициентов приведены в таблице.

Таблица

n	2	3	4	n	2	3	4
A n	0	1 / 4	1 / 2	m	0	1 / 24	1 / 12
B n	0	1 / 24	1 / 12	B m	0	— 1 / 8	— 1 / 4
C n	0	1 / 12	1 / 6	C m	0	0	0

Так, если по каждой стороне ячейки имеется только по одному соседу (того же размера n = 2, m = 2), выражение (10) переходит к виду для равномерной сетки, имеющему второй порядок аппроксимации по h (на оси – первый порядок). Однако, как только хотя бы по одной стороне появляется более одного соседа, в выражении (10) появляются члены, не зависящие от h . Например, для случая, когда ячейка справа граничит с двумя соседями (см. рис. 1) со стороной, вдвое меньшей, чем у самой этой ячейки ( n = 2, m = 2), в выражении (10) появляются члены, не зависящие от h

• R ₍ „.m ) = l (А) +* (^) +11 ( ^дУ ) + . ( h ) .           (_{П )}

4 \dz ² yi 24 \dr ² yi 12 ri \Эг yi

Из (9) — (11) следует, что при n = 3, m = 2 уравнение (9) принимает вид

Л^ = L1^ + w(h),(12)

где

5 d2^  25 d2^

L1^ 4 dz2 + 24 dr2 +12 r dr ’

Иными словами, аппроксимация оператора Л^ оператором L^ не является сходящейся, а вот аппроксимация оператора Л^ оператором L i ^ является сходящейся.

Таким образом, для оценки точности численного решения разностного уравнения Л^ = 0 нужно исследовать различия между решениями у и ^ i дифференциальных уравнений L^ = 0 и L i ^ i = 0. Эта разница отлична от нуля на неравномерной сетке и обращается в ноль на равномерной сетке.

2.    Различие предельного и точного решений модельной задачи

Пусть внутри осесимметричной конструкции в 2D цилиндрической геометрии в вакуумной области между двумя проводящими телами (катодом и анодом) (рис. 2) необходимо отыскать распределение потенциала электрического поля.

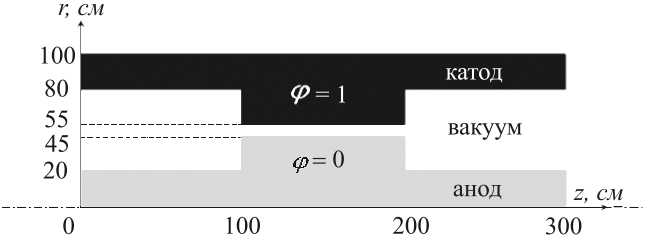
Рис. 2 . Геометрия модельной задачи

Для этого требуется решить уравнение Лапласа

1 £/ дА , дДдА =₀ r ∂r ∂r ∂z ∂z ^,

дополненное граничными условиями д£ I               =о

⁰ ,

^∂z z=0,z=300,20≤r≤80

^^l 0 < z < 100 ,r =20 = H100= ^ |200= Hz=100,20= И z=200,20= ⁰,

^ | 0= ^|100= ^|200= ^|z=100,55= ^|z=200,55= ¹•

Если ширина центрального катод-анодного зазора 45 < r <  55 существенно меньше его длины 100 < r <  200, а сам зазор расположен достаточно далеко от боковых границ счетной области, то реализуемое решение в сечении z = 150 см близко к одномерному, имеющему аналитическое выражение

^ ( r) — ln( ^r/r aHog ) / ln( ^r Kamog ^/r aHog ) •

Перейдем к безразмерной переменной R = r/ 45. На поверхности анода R = 1 , на поверхности катода R = 1 , 2222. Таким образом, решение одномерного уравнения в области 1 ≤ R ≤ 1 , 22225 имеет вид

ϕ ( R ) = 4 , 9833 ln R. (16)

Если в рассматриваемой одномерной задаче выбрать сетку с длиной интервалов, определяемой по геометрической прогрессии со знаменателем q = 2, то при h → 0 численное решение сходится к точному решению ϕ 1 = 44 , 3515 R ^1/9 - 1 дифференциального уравнения

L 1 ϕ 1 = ^∂ _∂ ^ϕ _r +⁹₈ r ^∂ _∂r ^ϕ 2 =0 .

В области 1 ≤ R ≤ 1 , 2222 модуль разности решений | ϕ - ϕ 1 | имеет вид

A y = 14 , 9833 In R - 44 , 3555 ^R ¹/⁹ - 1) | .

Определим максимальное значение ∆ ϕ . Функция ∆ ϕ ( R ) достигает максимума в точке

1 , 10486, где ^d _d ^∆ _R ^ϕ = 0 . В этой точке ^∆ _ϕ ^ϕ = 0 , 0054. Такое различие между предельным

R = при

h → 0 и точным решением вполне приемлемо, если параметры рассчитываемой установки задаются с точностью не выше 5 %.

3.    Экспериментальное определение скорости сходимости приближенного решения

Сходимость решений разностных задач в теории связывается с аппроксимацией и устойчивостью этих задач. Известно несколько вариантов соответствующих теорем ≪ эквивaлент-ности ≫ [7] – теорема Филиппова, [5, 9 – 11] – теорема Лакса, и во всех вариантах наличие аппроксимации является достаточным условием, но не необходимым. При этом порядок и вид нормы, в которой доказывается сходимость, определяются порядком и видом нормы имеющейся аппроксимации.

Рассмотрим, на примере модельной задачи, как сходится численное решение уравнения (17) к предельному решению. В качестве интегральной характеристики решения будем рассматривать по аналогии с [8] величину ψ , определяемую выражением

ψ =       | ϕ ( r i ) | r i ∆ r i .

i

Сначала определяется значение ψ 0 на базисной нерегулярной (адаптивной) сетке с числом ячеек сетки N 0 . Затем все сеточные ячейки делятся на две, то есть получаем удвоенное число ячеек сетки N 1 . Новое значение ψ обозначим ψ 1 . Далее, поступая аналогично, получим N 2 и ψ 2 . Введем безразмерный параметр ξ = N 0 /N _k и рассмотрим зависимость функции | ψ k - ψ k+1 | от ξ

ψ k = ψ 0 ξ ^β . (20)

При каждом последовательном удвоении числа точек эта зависимость приводит к выраже- нию для β

β = ln _ψ ^ψ _k+ ^k ₁     ln2 .

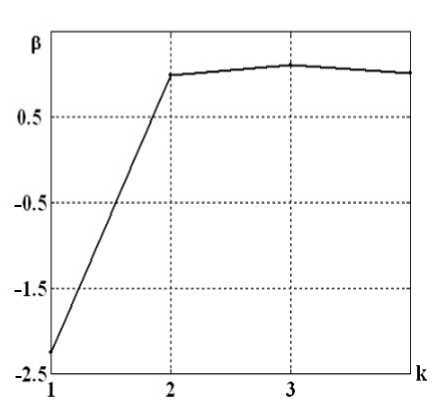
Результаты расчетов приведены на рис. 3. Из рис. 3 б видно, что при k >  2 значение β близко к 1. Иными словами, численное решение уравнения Λ 1 ϕ = 0 сходится к предельному решению, и скорость сходимости есть величина первого порядка. Разница между предельным решением, полученным на конкретной сетке, и точным решением уравнения Λ ϕ = 0 оценена в предыдущем параграфе.

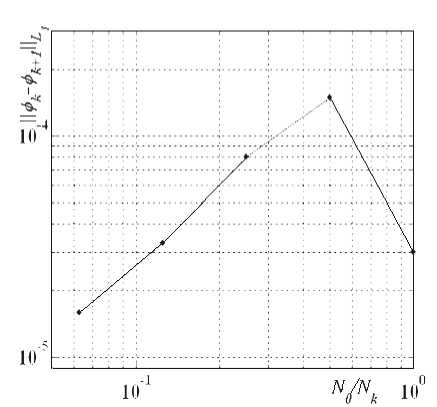
Рис. 3 . Сходимость (слева) и порядок сходимости (справа) в норме L 1 . N 0 – число ячеек базовой сетки, N _k – число ячеек k-й сетки, ξ _k = N ₀ /N _k

4.    Заключение

Проведено исследование одной разностной схемы для решения уравнения Лапласа на неравномерных сетках специального вида – адаптивно-встраиваемых с ячейками квадратной формы. Особенностью реализации было определение рассчитываемой функции – электрического потенциала – в центрах ячеек. Выстраиваемая из принципов интегро-интерполяционного подхода разностная схема на неравномерных сетках аппроксимирует дифференциальный оператор, отличный от исходного. Проведенные расчеты и оценки свидетельствуют о том, что порядок скорости сходимости приближенных решений, получаемых на неравномерных сетках, к предельному решению близок к единице: β ≈ 1 , и отличие предельного решения от точного не превосходит погрешностей задания параметров установки.

Работа проводилась при финансовой поддержке РФФИ Грант № 13-01-00072.