Математическое моделирование электромагнитного насоса с функциями дозирования перемешивания и подогрева

В настоящее время алюминиевая промышленность столкнулась с необходимостью повышения качества и производительности продукции в связи с острой конкуренцией на мировом рынке. Этот тренд выдвигает новые требования к технологиям производства, обусловливая необходимость поиска инновационных решений для удовлетворения потребностей рынка. В контексте высоких стандартов качества и эффективности, а также стремления к экономической эффективности научно-технический прогресс становится важным фактором успеха для предприятий алюминиевой промышленности. Поэтому исследования, направленные на разработку новых технологий и улучшение существующих производственных процессов, являются неотъемлемой частью стратегии развития данной отрасли.

В процессе производства алюминиевой продукции на этапе приготовления и литья металла качество и себестоимость готовой продукции зависит от многих факторов [1–4]. В число таких факторов входит создание однородного химического и температурного состава, а также подогрев жидкого металла на этапе приготовления алюминиевого сплава. Ко всему прочему на качество и скорость производства влияет выбор способа транспортировки жидкого алюминия от печи (миксера) до литейной машины.

Для решения выше указанных задач, как правило, используют несколько электротехно-логических установок, в лучшем случае на каждую задачу по одному устройству [5–7]. Если речь идет о приготовлении алюминиевого сплава в так называемом миксере, то для подогрева металла используют светящийся свод, для перемешивания жидкого металла применяют один из разновидностей перемешивателей, в том числе электромагнитные, ну и наконец для транспортировки используют, к примеру, транспортировочные ковши или электромагнитные насосы.

Предложенная ниже установка, разработанная на основе электромагнитного насоса с тройниковой рабочей зоной, позволяет решить сразу три задачи технологического процесса.

Перед тем как перейти к описанию результатов математического моделирования, в целях лучшего понимания материала статьи ниже приведена конструкция (рис. 1, 2) и принцип работы предлагаемого электромагнитного насоса.

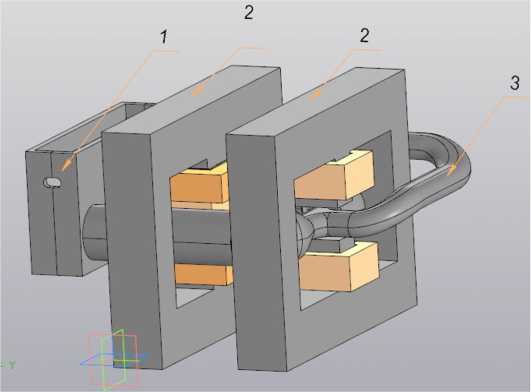
Рис. 1. Конструкция электромагнитного насоса, изометрия, где: 1 – футеровка насоса; 2 – магнитопроводы;

3 – обратный канал

Fig. 1. Design of an electromagnetic pump, isometry, where: 1 – pump lining; 2 – magnetic circuits; 3 – return channel

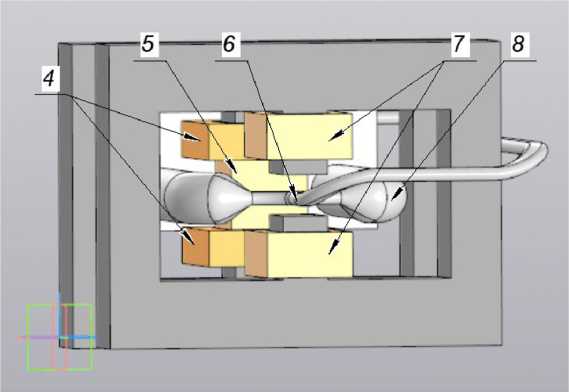
Рис. 2. Конструкция электромагнитного насоса, вид спереди (футеровка скрыта), где: 4 – дополнительные катушки основного индуктора; 5 – основной индуктор; 6 – тройниковая рабочая зона; 7 – катушки электромагнита; 8 – жидкий металл

Fig. 2. Electromagnetic pump design, front view (lining hidden), where: 4 – additional coils of the main inductor; 5 – main inductor; 6 – tee working area; 7 – electromagnet coils; 8 – liquid metal

– 946 –

Так как данная модель является лабораторной, для нее были приняты некоторые упрощения. В качестве металла был выбран металл с низкой температурой плавления – так называемый сплав Вуда, который плавится при температуре 60–70 0С [8]. Для экономии металла полноценной ванны печи не разрабатывалось, вместо нее был смоделирован небольшой прямоугольный накопитель металла.

Принцип работы представленной модели электромагнитного насоса основан на явлениях электромагнитной индукции и электромагнитного воздействия. В основном индукторе 5 протекает ток I осн , который создает в магнитопроводе 2 электромагнитное поле, которое пронизывает канал с металлом 8, в результате чего по законам электромагнитной индукции в металле наводится ЭДС – электродвижущая сила со сдвигом по фазе на 90⁰. Так как металл в канале замкнут сам на себя, в нем возникает ток большой величины, за счет протекания этого тока по металлу, металл нагревается и расплавляется. По катушкам электромагнита 7 также протекает ток I _ЭМ, который имеет сдвиг на 90⁰, создаваемый благодаря этому току, магнитное поле В пронизывает жидкий металл в тройниковой рабочей зоне 6. В результате чего на жидкий металл в этой зоне начинает действовать электромагнитная сила, направленная в сторону обратного канала, под воздействием данной силы металл приходит в движение и течет по обратному каналу в накопитель. Тройниковая рабочая зона имеет сечение намного меньше основного канала, это сделано в целях увеличения плотности тока и эффективности насоса, без такого сужения канала работа насоса практически невозможна [9].

Математическая модель ЭМ‑насоса

Математическое описание электромагнитных и гидродинамических процессов основано на взаимодействии сил электромагнитного поля с жидкими металлами с учетом формирующегося массопереноса. Система уравнений, описывающих электромагнитное поле, записанная относительно векторного и скалярного потенциалов (1–3), будет иметь вид [10]:

V2A - V(VA + £apa(d

V2

V8 = -(dpjdt),(3)

где: A – векторный потенциал, Вб/м; φ – скалярный потенциал неподвижных зарядов, В;– вектор плотности тока, А/м2; εа = 8,85 10–12, Ф/м – абсолютная диэлектрическая проницаемость; ρа – плотность свободных зарядов, Кл/м.

Значение вектора плотности тока, содержащегося в уравнениях (1, 3) определяется следующим уравнением:

• -           (8A\ _        _

8 = Y(~V

+ u x (V

x Л).                                 (4)

Для точного определения значений электромагнитного поля в области расчета к системе уравнений (1–3) следует добавить граничные условия. В расчетах применяются граничные условия, выраженные через векторный потенциал. Поскольку на границах индукторов поверхностные токи проводимости I равны 0, условия B_{n 2} – B_{n 1} = 0, H_{t 2} – H_{t 1} = 4 π i/c будут иметь следующий вид [10]:0

^n2 — All

^Т2 _ Al

^2  1«0|“1

Предполагая, что область расчета окружена средой с магнитной проницаемостью, значение которой стремится к бесконечности, на границах расчетной области будут выполняться условия [10]:

дА_т/дп — О

Ai = o

где n – нормаль к поверхности расчетной области.

Процессы гидродинамики, происходящие в модели, описываются уравнением движения жидкости (уравнение Навье-Стокса) (9). Жидкий металл, предложенный в модели, рассматривается как несжимаемый. Источником энергии движения жидкого металла в данном уравнении является удельная электромагнитная сила [10].

dv                   1     __

• — = -(у ■ V)v + vAv - -Vp + /_эм ,                                (9)

где: t – время, с; v – коэффициент кинематической вязкости, о.е.; ρ – плотность, кг/м³; p – давление, Па; V – векторное поле скорости, м/с; £ – векторное поле электромагнитных сил, Н.

Для решения уравнения Навье-Стокса были приняты граничные условия:

• 1.    Стенка футеровки непроницаема для жидкости. На внутренней поверхности футеровки нормальная составляющая скорости равна нулю Vn =0.

• 2.    Условие прилипания жидкости к твердой стенке. На внутренней поверхности футеровки тангенсальная составляющая скорости равна нулю Vτ =0.

• 3.    Условие свободного скольжения жидкости вдоль поверхности. На свободной поверхности жидкости, над которой находится газ (вакуум), задается нулевая нормальная производная тангенциальной составляющей скорости dVτ / dVn = 0.

• 4.    Принято, что жидкость не сжимаемая ρ = const [10].

Начальным условием для уравнения гидродинамики является распределение скоростей жидкости по всему объему. В нашей задаче в начальный момент времени жидкость статична, поэтому скорость в каждой точке объема равна 0.

Математическое моделирование электромагнитных и гидродинамических процессов

В программе ANSYS Maxwell было выполнено построение математической модели, которая позволила решить электромагнитную задачу. Построение математической модели для решения электромагнитной задачи было выполнено в программе ANSYS Maxwell.

Для упрощения решения электромагнитной задачи в математической модели был принят следующий ряд допущений:

• •    Пренебрежение тепловыми процессами;

• •    Геометрия жидкой части слитка постоянна;

• •    Пренебрежение движением жидкого металла в электромагнитной задаче;

• •    Пренебрежение токами смещения;

• •    Воздушный зазор является равномерным;

• •    Пренебрежение электропроводностью магнитопровода;

• •    Конструкция модели упрощена.

Анализ результатов

В качестве рабочей жидкости, которую насос будет перекачивать, был выбран сплав Вуда, он обладает низкой температурой плавления (температура плавления в пределах 60–70 0С), данное условие позволяет упростить построение лабораторной физической модели.

В табл. 1 указаны значения физических свойств используемых материалов, таких как удельное сопротивление, магнитная проницаемость, плотность, вязкость.

Решение математической задачи программа произвела за 6 итераций, конечная энергетическая ошибка составила err=2,76 %, такое значение ошибки говорит о том, что большое количество итераций не требуется, задача решена с высокой точностью.

Таблица 1. Материалы и их свойства

Table 1. Materials and their properties

Материалы	Удельная проводимость, см/м	Магнитная проницаемость, о.е.	Плотность, кг/м3	Вязкость, па*с
Электротехническое железо (магнитопровод)	0	800 (в номинальном режиме работы)	-	-
Медь (катушки)	58000000	1,0	-	-
Сплав Вуда (жидкая часть слитка)	435000	1,0	9720,00	0,0041
Вакуум	0	1,0	-	-

Таблица 2. Параметры катушек

Table 2. Coil parameters

Материалы	Количество витков	Диаметр проводника катушки, мм	Номинальная величина тока, А	Частота, Гц
Основной индуктор	200	1,0	3,14	50,0
Дополнительные катушки основного индуктора	2 катушки по (480 витков)	1,0	3,14	50,0
Катушки электромагнита	2 катушки по (550 витков)	1,0	3,14	50,0

Результаты моделирования

Распределение плотности тока в расчетной области

Для анализа глубины проникновения электромагнитного поля и выделения тепловой энергии была получена картина распределения плотности тока в модели, результы которой – 949 –

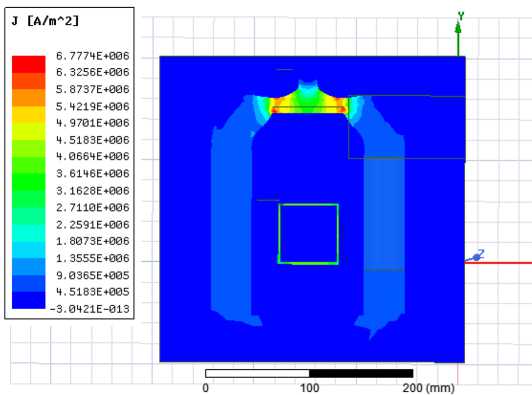
Рис. 3. Распределение плотности тока в модели

Fig. 3. Current density distribution in the model представлены на рис. 3. Как видим, при частоте тока 50 гц плотность тока по сечению канала распределена равномерно, это говорит о том, что поверхностный эффект при такой частоте проявляется слабо. Максимальная плотность тока достигается в тройниковой рабочей зоне модели, это связанно с тем, что в этой зоне продольное сечение канала в разы меньше, чем в основной части.

Распределение тепловой энергии в расплаве

Распределение тепловой энергии (рис. 4) в модели соответствует картине распределения плотности тока, что полностью соответствует закону Джоуля-Ленца. При работе насоса в ре-

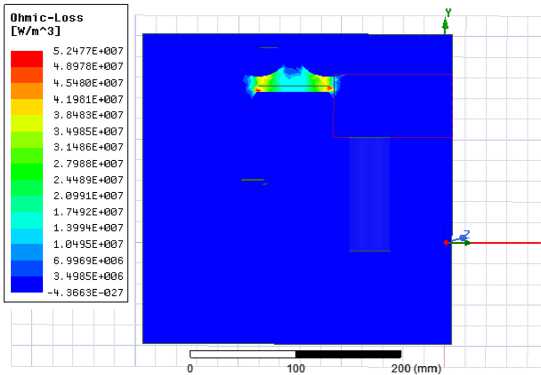
Рис. 4. Распределение выделения Джоулевой энергии в модели

Fig. 4. Distribution of Joule energy release in the model жиме нагрева возможен локальный перегрев в тройниковой рабочей зоне. Перегрев возможно уменьшить с помощью дополнительного перемешивания расплава в этой зоне при помощи двух дополнительных катушек. Эффект работы дополнительных катушек рассмотрен ниже. Общая тепловая мощность, выделяемая в расплаве установки, составляет 589 Вт. По расчетам время нагрева и расплавления металла составит приблизительно 12 минут.

Магнитное поле в рабочей зоне

Для анализа магнитного поля были получены дифференциальные характеристики распределения напряженности магнитного поля H и магнитной индукции В. На рис. 5а, 5б представлены картины магнитных полей от основного индуктора. Как видно из рис. 5а, максималь-

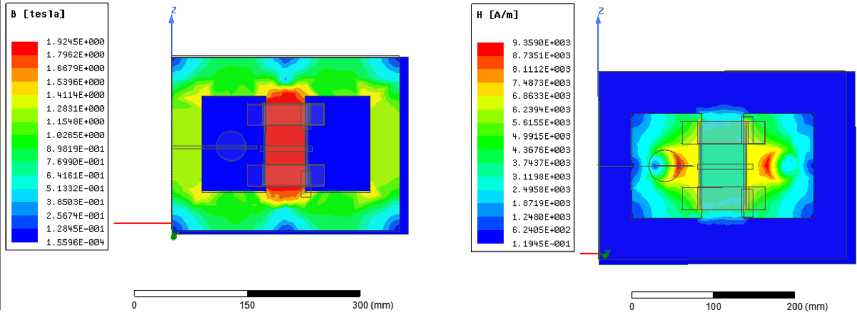
магнитной индукции

Рис. 5б. Распределение напряженности магнитного поля от основного индуктора

Рис. 5а. Распределение от основного индуктора

Fig. 5a. Distribution of magnetic induction from the main inductor

Fig. 5b. Distribution of magnetic field strength from the main inductor

ное значение магнитной индукции достигает 1.92 Тл, для выбранной марки трансформаторной стали 2013 данное значение является допустимым.

На рис. 6а, 6б представлены картины распределения магнитной индукции и напряженности магнитного поля соответственно от индуктора электромагнита, магнитная индукция в магнитопроводе имеет достаточно низкие значения. Распределение напряженности магнитного поля в рабочей зоне имеет сконцентрированный характер, основная часть которого сосредоточена в тройниковой рабочей зоне, это говорит о том, что размеры рабочей зоны насоса и ширина магнитопровода подобраны оптимально.

Энергетические характеристики индукторов

По каждому из индукторов был сделан расчет энергетических характеристик, результаты которых приведены в табл. 3. Расчеты проводились по формулам, приведенным ниже.

Реактивная мощность, ВАР:

Q = 2E2nf,                                                        (10)

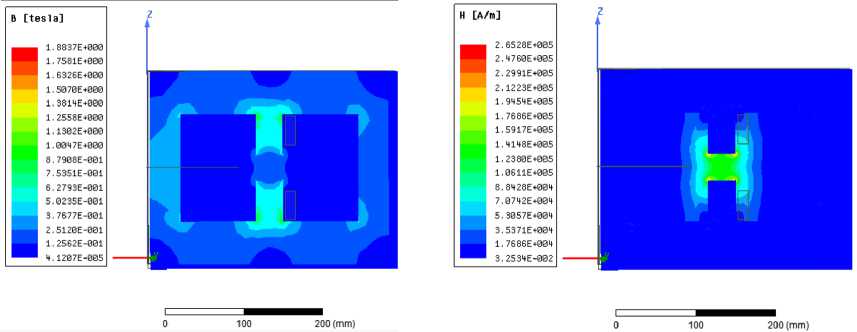
Рис. 6а. Распределение магнитной индукции от индуктора электромагнита

Fig. 6a. Distribution of magnetic induction from the electromagnet inductor

Рис. 6б. Распределение напряженности магнитного поля от индуктора электромагнита

Fig. 6b. Distribution of magnetic field strength from the electromagnet inductor

Полная мощность, ВА:

S^y/P2+Q2i(11)

Коэффициент мощности, о.е;:

cos = P/S,(12)

Напряжение, В:

U = S/I,(13)

где: Е – энергия магнитного поля, Дж; P – активная мощность, Вт; f – частота переменного тока, Гц; I – действующее значение тока, А.

Параметры индукторов подбирались такими, чтобы номинальные токи соответствовали значению напряжения в 230В, при значении тока в катушке 3,14 А. Коэффициент мощности дополнительных катушек достаточно низкий, для его повышения необходимо будет использовать конденсаторы.

Таблица 3. Энергетические параметры индукторов

Table 3. Energy parameters of inductors

Наименование катушки	E (из программы), Дж	Q, ВАР	P (из программы), Вт	S, ВА	Cos, о.е.	U, В
Основной индуктор	0,66	414,48	589,00	720,21	0,8178	230,05
Дополнительные катушки основного индуктора	0,739	464,09	60,00	467,95	0,1282	149,47
Катушка электромагнита	1,129	709,01	37,34	709,99	0,0526	226,78

Зависимость электромагнитных сил от тока Iэм при номинальном значении тока Iосн

Задачей расчёта электромагнитной задачи является определение электромагнитных сил в расплаве. На рис. 7 представлено распределение электромагнитных сил в тройниковой зоне при значении тока в основном индукторе и индукторе электромагнита 4 А. Распределение сил в рабочей зоне достаточно равномерно, поэтому для получения графиков зависимости электромагнитных сил от величины тока достаточно одной точки, в качестве такой точки была выбрана центральная точка тройниковой рабочей зоны. Зависимости электромагнитных сил от величины тока в катушках электромагнита при номинальном токе в основном индукторе представлены в табл. 4.

На основе электромагнитных сил, полученных при решении электромагнитной задачи, в программе ANSYS CFX была решена гидродинамическая задача, главным результатом которой является распределение скоростей жидкого металла (рис. 8). Была получена зависимость скорости жидкого металла от величины тока электромагнита. В качестве точки измерения была выбрана точка в обратном канале установки, на рис. 8 данная точка обозначена красным перекрестием. Данная точка выбрана по причине наиболее равномерного распределения

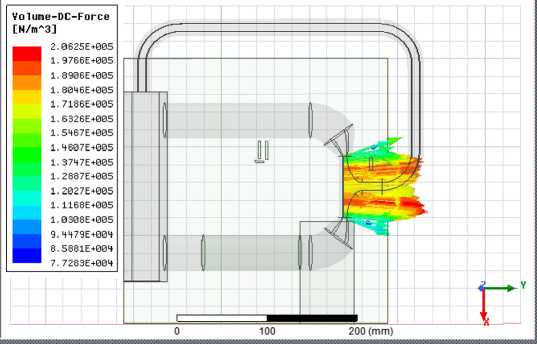
Рис. 7. Распределение электромагнитных сил в рабочей зоне

Fig. 7. Distribution of electromagnetic forces in the working area

Таблица 4. Значение электромагнитных сил и скорости потока от величины тока

Table 4. The value of electromagnetic forces and flow velocity from the current value

Значение тока А осн, 3,14 3,14 3,14 3,14 3,14 3,14 3,14 Значение тока Iэм, А 0,0 0,785 1,57 2,355 3,14 3,925 4,71 Значение электромагнитной силы, Н 0,393⸱105 0,755⸱105 1,09⸱105 1,39⸱105 1,68⸱105 1,90⸱105 2,13⸱105 Скорость м/с 0,089 0,179 0,231 0,268 0,356 0,384 0,406 скорости в обратном канале. Результаты измерения представлены в виде табличных данных (табл. 4) и в виде графиков зависимости скорости от величины плотности тока (рис. 9)

Зависимость электромагнитных сил от тока Iосн при номинальном значении тока Iэм

Были построены графики зависимости электромагнитных сил и скоростей от значения тока основного индуктора и индуктора электромагнита, которые представлены на рис. 9 и 10.

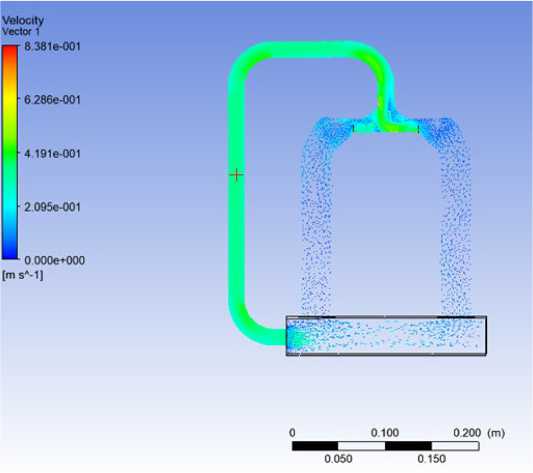
Рис. 8. Распределение скоростей жидкого металла в модели

Fig. 8. Distribution of liquid metal velocities in the model

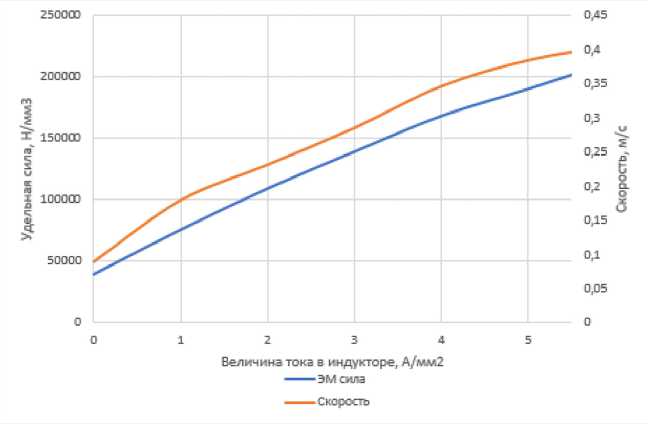
Рис. 9. График зависимости электромагнитных сил и скорости от значений тока I _эм

Fig. 9. Graph of the dependence of electromagnetic forces and speed on current values I _эм

Таблица 5. Значение электромагнитных сил и скорости потока от величины тока

Table 5. The value of electromagnetic forces and flow velocity from the current value

Значение тока Т А осн,	0,0	0,785	1,57	2,355	3,14	3,925	4,71
Значение тока Г А эм,	4,0	4,0	4,0	4,0	4,0	4,0	4,0
Значение электромагнитной силы, Н	-2,66⸱103	1,139⸱104	3.32⸱104	7,04⸱104	1,68⸱105	2,26⸱105	2,60⸱105
Скорость течения жидкого металла	0	0,104	0,159	0,224	0,401	0,412	0,416

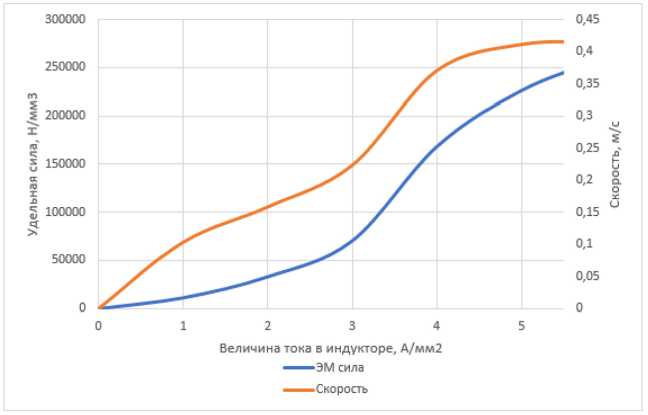
Рис. 10. График зависимости электромагнитных сил от значений тока

Fig. 10. Graph of the dependence of electromagnetic forces on current values I осн

Как видим, зависимости данных сил от значения тока имеют практически прямолинейный характер, такая зависимость позволит упростить управление гидродинамическими параметрами насоса (расход/давление). При номинальных значениях тока в обоих индукторах удельная электромагнитная сила составила 1,68⸱105 Н/м3, по расчетам значение такой силы может позволить поднять выбранный металл на высоту 11см.

Функция перемешивания

В конструкции данного насоса предусмотрена функция перемешивания металла внутри самого канала. Осуществляется она при помощи двух дополнительных катушек, представленных на рис. 2 под номером 4. По данным катушкам протекает ток с временным сдвигом по фазе в 900 по отношению тока основного индуктора, в результате чего создается вращающееся магнитное поле, которое приводит в движение жидкий металл в основной части канала. На рис. 11а и 11б представлены результаты воздействия электромагнитных сил на жидкий металл, результаты представлены в виде векторной картины распределения скоростей расплава в основном канале. Движение металла имеет вращательно-поступательный характер.

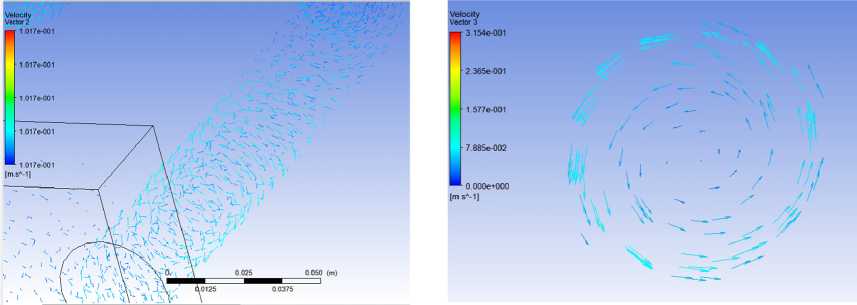
Рис. 11б. Распределение скоростей жидкого металла в основном канале (в сечении)

Рис. 11а. Распределение скоростей жидкого металла в основном канале (общий вид)

Fig. 11a. Distribution of liquid metal velocities in the main channel (general view)

Fig. 11b. Distribution of liquid metal velocities in the main channel (in cross section)

Если эксплуатировать подобный насос для перекачки расплавленного алюминия, канал насоса быстро зарастет оксидом алюминия. Создание вращательного движения металла в канале позволит очищать поверхность канала от зарастания.

Вывод

Используя методы математического моделирования, была проверена на работоспособность модель электромагнитного насоса с дополнительными функциями. Также был проведен анализ электромагнитных и гидродинамических процессов, происходящих в данной модели.

Материалы проведения расчета численной модели представлены в виде картин распределения дифференциальных и векторных значений электромагнитных сил, плотностей тока, выделения тепловой энергии и характеристик магнитного поля. Были получены графики зависимости электромагнитных сил, действующих на жидкий металл, от величин тока. Гидродинамическая модель позволила определить картину распределения скорости жидкого металла.