Математическое моделирование электронных процессов и кинетика ионизации глубоких уровней

Интерес к изучению спектра глубоких энергетических состояний в запрещённой зоне полупроводниковых материалов обусловлен тем, что они влияют на их параметры гораздо сильнее, чем мелкие центры локализации заряда [1]. Современная спектроскопия глубоких уровней (ГУ), в основном, сосредотачивает своё внимание только на определении параметров глубокоуровневых центров, таких как энергия ионизации, сечение захвата и концентрация. При этом вопрос об их состоянии в данный момент времени при конкретной температуре и напряжении остаётся не до конца изученным. Необходимость формирования таких представлений о кинетике перезарядки ГУ обусловлена двумя причинами. Во-первых, все методики спектроскопии ГУ являются релаксационными, то есть поведение каждого глубокоуровневого центра подчиняется закономерностям неравновесной статистики. Ввиду сложности этих закономерностей для анализа спектральных зависимостей используются упрощённые модели кинетики перезарядки ГУ [1–3]

Это влечёт за собой значительное увеличение методологической погрешности определения параметров этих центров [4]. Для снижения величины данной погрешности необходимо определить допустимые границы упрощения соответствующих математических моделей. Во-вторых, все полупроводниковые приборы, использующие принцип переключения, работают при неравновесных условиях, то есть поведение как свободных, так и связанных зарядов в них подчиняются тем же закономерностям неравновесной статистики.

Поскольку ГУ играют значительную роль в процессах термической генерации и рекомбинации неравновесных носителей заряда, то формирование чётких представлений о кинетике их ионизации позволит определить пути оптимизации функционирования таких приборов.

В настоящее время для анализа кинетики перезарядки дискретных ГУ используются стадийные модели [1–5]. Они предполагают, что каждый глубокоуровневый центр ионизируется в определённом узком интервале температур. Дальнейшее увеличение температуры не приводит к значительному изменению его состояния. Границы этого интервала определяются в первую очередь глубиной дискретного уровня. Величина же сечения захвата ГУ и его концентрация влияют, в большей степени, на скорость увеличения заряда на нём. Ионизированный ГУ при более высоких температурах уже не вносит существенного вклада в изменение, например, ёмкости диода Шоттки или p-n-перехода.

Такими свойствами обладает в первую очередь «одноуровневые» модели, в которых учитывается либо только термическая генерация носителей заряда с уровня в одну из разрешённых зон [1–2], либо как в работе [3] для ГУ, находящихся в средине запрещённой зоны, термоэмиссия электронов в зону проводимости и перезахват электронов из валентной зоны на ионизированный донор. Достоинством «одноуровневых» моделей является относительная простота их использования при анализе спектров ГУ. К числу недостатков следует отнести тот факт, что в них не учитывается процессы обмена носителями заряда между уровнями, а также процессы рекомбинации заряда на ГУ.

Частично устранить эти недостатки позволили «двухуровневые» модели [4, 5]. В работе [4] предложена кинетика перезарядки двух ГУ с учётом процессов термоэмиссии электронов с ГУ в зону проводимости, а также процессов обменена носителями заряда между уровнями и обеими разрешёнными зонами. В свою очередь в работе [5], была рассмотрена «двухуровневая» модель на базе кинетики Шоккли– Рида, учитывающая помимо вышеназванных ещё и процессы рекомбинации свободных носителей заряда через эти ГУ. Рассматриваемые модели являются более точными, чем «одноуровневые». Тем не менее они также не лишены стадийного характера.

Деление процесса перезарядки ГУ в запрещённой зоне полупроводника на стадии является искусственным приёмом с одной стороны, облегчающим определение параметров центров локализации заряда, с другой – искажающим реальную картину этого явления. Перезарядка ГУ представляет собой непрерывный динамический процесс, характер которого определяется не только временем, температурой и величиной напряжения, подаваемого на структуру, но и совокупностью параметров всех уровней в запрещённой зоне полупроводника.

В связи со сказанным, целью работы является: во-первых, создание адекватной модели кинетики перезарядки дискретных глубокоуровне-вых центров в запрещённой зоне полупроводника, учитывающей влияние каждого из них на процессы генерации и рекомбинации свободных носителей заряда, во-вторых, применение данной модели для анализа характера ионизации донорных уровней в запрещённой зоне арсенида галлия (GaAs) – полупроводника, широко используемого в современной электронике.

• 1.1    Кинетика перезарядки глубоких уровней

Кинетика перезарядки ГУ в работе рассматривается без учёта влияния на процесс внешнего электрического поля. Для полупроводника, у которого в запрещённой зоне имеется m дискретных глубоких донорных уровней, будем считать, что при каждом значении температуры T на гетероструктуру подаётся импульс прямого напряжения смещения, и переводит систему из состояния термодинамического равновесия в отсутствие внешнего кулоновского поля в состояние термодинамического равновесия при наличии такового. После снятия со структуры внешнего напряжения система зарядов самопроизвольно возвращается в исходное состояние.

Все процессы, приводящие к перезарядке каждого конкретного ГУ, сопровождаются либо поглощением, либо выделением энергии в той или иной форме в единице объёма полупроводника. Для любого i-го энергетического состояния можно определить мгновенное значение объёмной плотности тепловой мощности процесса перезарядки, которая равна

Цi , t , T ) = А ( i , t , T ) [ N i - n ( i , t , T ) ] -

• -B ( i, t, T ) n ( i, t, T )              , ⁽¹⁾

где i -ое энергетическое состояние характеризуется четырьмя параметрами ( a p ( i ) - сечение захвата для дырок, a n ( i ) - сечение захвата для элеронов, N i - концентрация и E i - энергия), t - время, А ( i, t, T ) - мгновенная мощность, поглощаемая при данной температуре T в процессе перезарядки i -го энергетического состояния, n ( i , t , T ) - концентрация дырок на i -ом энергетическом состоянии, В ( i , t , T ) - мгновенная мощность, выделяемая при данной температуре в процессе перезарядки i -го энергетического состояния. Следует отметить, что величины срi , t , T ) , А ( i , t , T ) и B ( i , t , T ) с одной стороны являются функциями непрерывных переменных t и T , с другой - функциями дискретной переменной i .

Очевидно, что для каждого значения T перераспределение энергии, путём перехода носителей заряда из одного энергетического состояния на другое, будет осуществляться в направлении m (i, t, T ) = min . Кроме того, для данной температуры при выполнении условия Vim(i,t,T) = const в полупроводнике достигается термодинамическое равновесное распределение зарядов. Исходя из этого, кинетику перезарядки ГУ, можно описать в виде следующего дифференциально-разностного уравнения

' m (i, t, T)- m (i +1, t, T) — dn (i, t, T) = , dt

E , — E i + 1

m ( i , t , T ) - m ( i - 1, t , T )

E i - E i - i

V i e [ 0, m ]

i = m + 1

Граничные условия для системы уравнений (1-2) имеют вид:

/ i = 0, Ei = Ec, n (i, t, T) = [ N (T)- ne (t, T)], Ni = ne (t, T) (3) '_ i = m +1, Ei = Ev, n (i, t, T ) = p (t, T), N = Nv (T)     , где Ec - нижний край зоны проводимости (ЗП), Ev - верхний край валентной зоны (ВЗ), Nc (T) - эффективная плотность состояний в ЗП, Nv (T) - эффективная плотность состояний в ВЗ, ne (t, T) - концентрация свободных электронов в ЗП, p (t, T) - концентрация свободных дырок в ВЗ. Поскольку в зоне проводимости нет дырок, то величина n (0, t, T) интерпретируется как концентрация свободных мест для электронов.

Помимо граничных условий, на систему уравнений (1-2) налагаются начальные условия ne ( 0> T )= ne 0 (T )

• •           p (0. T ) = p 0 ( T )          ,    (4)

n ( i ,0, T ) = n ₀ ( i , T ) , V i e [ 0, m + 1 ]

где ne0 (T) и p0 (T) - соответственно концентрации свободных электронов и дырок в начальный момент времени, n0 (i, T) - кон- центрация дырок на энергетических состоя- ниях.

В уравнении (1) величина коэффициентов А ( i , t , T ) и В ( i , t , T ) определяется совокупностью процессов генерации и рекомбинации зарядов как в разрешённых зонах, так и на ГУ. Поэтому их можно представить в следующем виде

А ( i , t , T ) = a n ( i , t , T ) + U p ( i , t , T ) (₅) \B ( i , t , T ) = p p ( i , t , T ) + p n ( i , t , T ) , ⁽⁾

an (i, t, T ) = где i-1

= Z ^a n ( i ) ^V n ( ^T ) ⁿ ( j , t , ^T ) ^exp j = 0 _

E^^E j !( E, - E )1⁽⁶⁾ kT j *’

поглощаемая мощность, обусловленная термоэмиссией электронов с i-го ГУ на дырки, находящиеся на более высоких энергетических состояниях, k – постоянная Больцмана.

Для i = m + 1 выполняются условия:

" n ( i ) = " p ( j ) . V ( ^T ) = V p ( ^T ) .

Здесь Vp (T) и Vn (T) - тепловые скоро- сти дырок и электронов соответственно. Последнее условие соответствует рекомбинации дырок на j-ых уровнях, за счёт перехода на них электронов из валентной зоны.

ap (i, t,T ) = m+1

= 2

j = i + 1

( E. - E. Y

" p ^{( j} ) V p ^{( T} ) n ^{( j} , t , ^T ) exp V -^kf- J ( E i ^— E j )

Это соотношение описывает прирост энергии в единицу времени на i -ом энергетическом состоянии, обусловленный переходом с него электронов на дырки, расположенные на более низких уровнях, с последующей рекомбинацией этих зарядов. На это уравнение налагается        граничное        условие

" _p ( m + 1 ) = " _n ( i ) , которое характеризует процесс рекомбинации электрона с ГУ и свободной дырки из валентной зоны.

Коэффициент в (i, t,T ) = m+1

2 " n ( j ) V n ( T ) [ N j

—

n

/      \"l    ( E j — E i ^/        \

( ^j , t , ^T ) ] exp I ——l ( ^E i ^— E j )

V ^kT    J

есть мощность, выделяемая при переходе на дырки, находящиеся на i-ом ГУ, электронов с более низких энергетических состояний. Как и в предыдущем случае, для этого соотношения имеется граничное условие "n (m +1) = "p (i), которое характеризует процесс перехода электронов из валентной зоны на ионизированный ГУ.

Аналогично

P n ( i , t , T ) =

i — 1

= 2

j = 0

" p ⁽ i ) V p ^{( T} ) [ N j ^{— n ( j} , t , ^T ) ] exp ⁽ EkE J ( E j ^— E )

есть энергия, выделяемая в единицу времени при переходе на дырки, находящиеся на i -том энергетическом состоянии, электронов с более высоких уровней.

На это уравнение налагаются условия: при i = m ^{+ 1} " p ( i ) = " n ( j ) , V p ( T ) = V n ( T ) , ^ко торые соответствуют рекомбинации дырок в валентной зоны за счёт падения на них электронов с более высоких уровней.

• 1.2 Анализ характера ионизации дискретных глубоких донорных уровней в арсениде галлия.

С целью выявления особенностей ионизации ГУ в GaAs при различных температурах, было проведено численное моделирование этого процесса для совокупности шести центров локализации заряда. Для определённости рассмотрим диод Шоттки Me — GaAs . Параметры этих уровней (таблица 1) были взяты из работы [6]. В работе предполагалось, что V i e [ 1, m ] " n ( i ) « " _p ( i ) . Значение " _p ( 0 ) и

"n (0), используемые при вычислении коэффициентов (6, 9), характеризующие прямые пере- ходы зона-зона, оценивались из соотношения r3KCV, (To)[Nv (To) — p(To )]x

" =

^{X[ N}c ( ^T 0 ) — n e ( ^T 0 ) ] exp

— 1

,(10)

E g

kT 0

V

где т _экс = 3,7 • 10 ^{— 7} с - экспериментальное значение времени жизни неравновесных носителей заряда при температуре T ₀ = 300 K [7], p ( T ₀ ) и n e ( T ₀ ) - равновесные концентрации свободных носителей в зонах при данной температуре, определяемые из решения уравнения электронейтральности для GaAs с уровнем легирования ~ 10¹⁶ см^-3, E_g – ширина запрещённой зоны арсенида галлия. При этом предполагалось, что " n ( 0 ) = " _p ( 0 ) = " .

Таблица 1

Параметры глубоких уровней

Table 1

Deep levels parameters

i	E c — E , эВ	" n ( i ) ,см 2
1	0,13	3·10-16
2	0,2	9·10-16
3	0,35	1,6·10-14
4	0,41	1,5·10-14
5	0,6	1,4·10-13
6	0,84	6·10-14

Будем считать, что импульс напряжения прямого смещения, подаваемого на диод Шоттки и, выводящий систему из термодинамического равновесия, имеет амплитуду и длительность, обеспечивающие для каждой температуры на момент времени t = 0 выполнение условий:

п_е 0 ( T ) = 0; p 0 ( T ) = 0; n 0 ( i , T ) = 0, V i e [ 0, m + 1 ] .

Результаты численного эксперимента с использованием предлагаемой в работе модели кинетики перезарядки ГУ в рамках описанных выше приближений представлены на рисунках 1–3. Из анализа этих зависимостей можно сделать следующие выводы.

Во-первых, рекомбинация заряда на энергетических состояниях оказывает существенное влияние на кинетику перезарядки ГУ. В частности, при релаксации системы в отсутствии внешнего электрического поля интенсивность процесса рекомбинации оказывается выше, чем если существует обратное смещение на диоде. Это приводит к смещению максимумов степеней ионизации ГУ в сторону более высоких температур (рисунки 1–2).

В частности, глубокие уровни i = 1 и i = 2 (рисунки 1–2, зависимости 1, 2) обычно не наблюдаются на реальных DLTS-спектрах при температурах выше 100 К. В этом случае эти центры локализации заряда регистрируются в температурном интервале от 100 до 200 K (рисунки 1a, 2a, зависимость D). Кроме того, ГУ i = 5 и i = 6 на реальных спектрах, измеренных при величине обратного смещения, наблюдаются в диапазоне температур (240– 280) K и (320–380) K, соответственно. В этом случае ионизация ГУ начинается при температуре (рисунки 1–2, зависимости 5 и D). При этом существенной ионизации ГУ в диапазоне температур не происходит.

(a)

Рисунок 1. Температурные зависимости степени ионизации ГУ (1–5) и DLTS-спектр (D): (a) для момента времени t = 1 c, спектр рассчитан при t 1 = 0,1 c, t ₂ = 0,5 c (b) для момента времени t = 2 c, спектр рассчитан при t 1 = 0,01 c, 1 ₂ = 1,9 c ( N 1 i = 10¹³ V i e [ 1,6 ] )

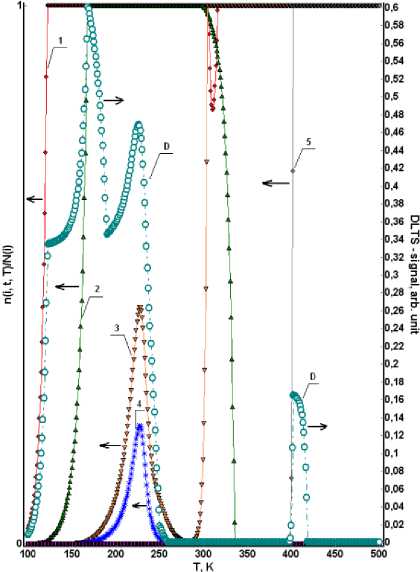
(b)

Figure 1. The temperature dependence of the degree of ionization DL (1–5) and DLTS-spectrum (D): (a) for points in time t = 1 s, the spectrum calculated at t1 = 0,1 s, 12 = 0,5 s (b) for points in time t = 2 s, the spectrum calculated at t1 = 0,01 s, 12 = 1,9 s (N1 i = 1013 Vi e [1,6])

Во-вторых, учёт генерационных и рекомбинационных составляющих процесса перезарядки всей совокупности ГУ в запрещённой зоне полупроводника приводит к выводу о том, что кинетика ионизации этих центров в общем случае не подчиняется больцманов-ской статистике.

Об этом свидетельствуют в первую очередь аррениусовские зависимости (рисунок 3). Видно, что линейному закону подчиняются только четыре зависимости (рисунок 3, зависимости 1, 1a, 1b, 2). Значения энергий ионизации ГУ, рассчитанные на основании этих данных приведены в таблице 2.

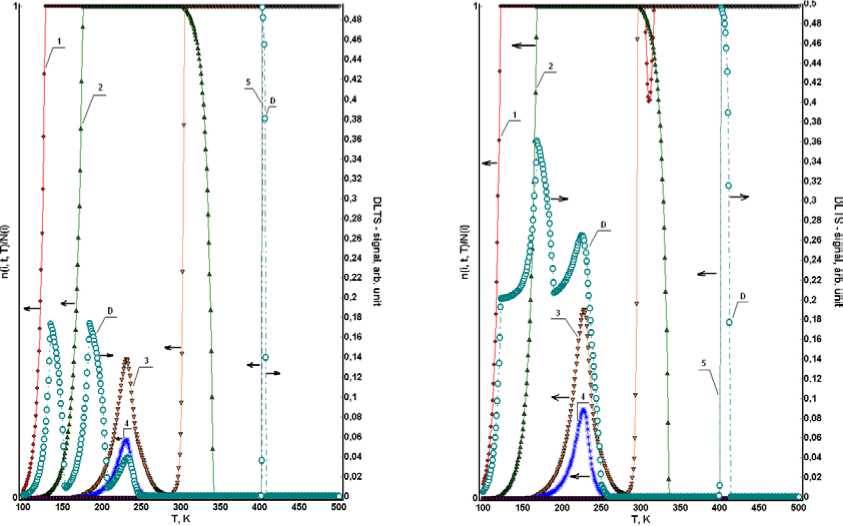
(a)                                                       (b)

Рисунок 2. Температурные зависимости степени ионизации ГУ (1–5) и DLTS-спектр (D): (a) для момента времени t = 1 c, спектр рассчитан при t 1 = 0,1 c, t 2 = 0,5 c (b) для момента времени t = 2 c, спектр рассчитан при t 1 = 0,01 c, 1 ₂ = 1,9 c ( N 1 i = 10¹³ V i е [ 1,4 ] л i = 6; N ₅ - 10¹³ см^-3)

Figure 2. The temperature dependence of the degree of ionization DL (1–5) and DLTS-spectrum (D): (a) for points in time t = 1 c, the spectrum calculated at t1 = 0,1 c, 12 = 0,5 c (b) for points in time t = 2 c, the spectrum calculated at t1 = 0,01 c, 12 = 1,9 c (N1 i = 1013 Vi е[1,4]лi = 6; N5-1013 см-3)

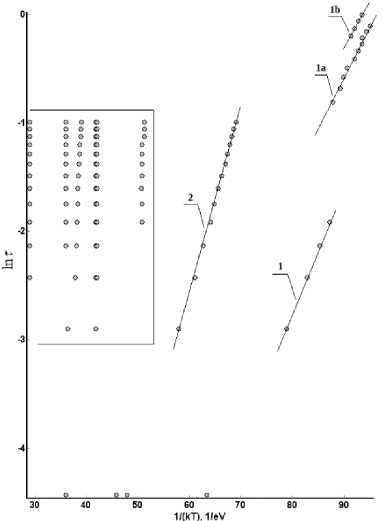
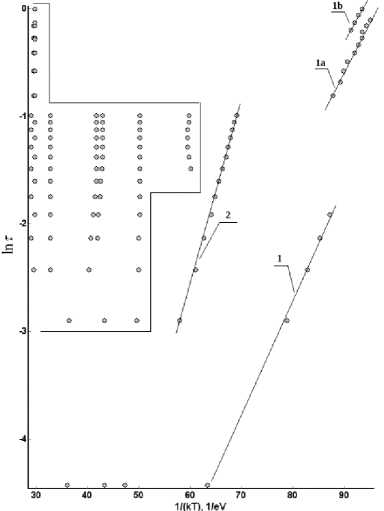
• (a)                                                       (b)

Рисунок 3. Аррениусовские зависимости для ГУ в GaAs, рассчитанные с использованием уравнений (1–2): (a) N 1 i = 10¹³ V i е [ 1,6 ] ; (b) N 1 i = 10¹³ V i е [ 1,4 ] л i = 6; N ₅ - 10¹³ см^-3

Figure 3. Arrhenius dependence for DL in GaAs, calculated using the equations (1-2): (a) N 1 i = 10¹³ V i е [ 1,6 ] ; (b) N 1 i = 10¹³ V i е [ 1,4 ] л i = 6; N ₅ ■ 10¹³ см^-3

Таблица 2

Рассчитанные значения энергии ионизации глубоких уровней

Table 2

Simulated values of deep levels ionization energies

Рисунок	Зависимость	E c – E эВ
3-а	1	0,116
3-а	1a	0,095
3-а	1b	0,085
3-а	2	0,189
3-б	1	0,107
3-б	1a	0,096
3-б	1b	0,096
3-б	2	0,177

Как видно из таблицы 2, больцманов-скому закону подчиняются кинетики перезарядки только низкотемпературных центров i = 1 и i = 2, причём только в определённых временных интервалах (рисунок 3, зависимости 1 и 2). В то же время зависимости 1-a и 1-b на рисунок 3 можно считать проявлением ГУ i = 1. При этом наблюдается значительная погрешность в определении энергии ионизации, что свидетельствует о незначительном отклонении кинетики перезарядки этого центра от закономерностей больцмановской статистики. В тоже время для других ГУ (рисунок 3, выделенные области) это отклонение является более существенным. Если же исходить из предположения, что это не так, тогда следует вывод о бесконечно большой энергии ионизации ГУ с i > 2 (зависимости в выделенных областях на рисунке 3 представляют собой практически вертикальные линии).

Очевидно, что электрическое поле, в зависимости от его направления, смещает динамическое равновесие между генерационными и рекомбинационными составляющими процесса перезарядки ГУ. Поэтому при подборе определённой величины напряжения обратного смещения, подаваемого на диод, можно снизить влияние процесса рекомбинации заряда на кинетику перезарядки ГУ, и добиться линеаризации соответствующих аррениусовских зависимостей (это и происходит при измерении реальных DLTS-спектров). Но, при этом оказывается, что получаемые значения энергий ионизации ГУ являются функционально зависимыми от величины напряжения обратного смещения.

В-третьих, процессы обмена зарядами между различными ГУ также оказывают существенное влияние на кинетику их перезарядки. Это приводит к тому, что ГУ, отвечающие условию Et - E+1 < 4 kT, оказываются принципиально неразличимыми при DLTS-спектроскопии по методу [2]. Этот факт следует из анализа зависимостей 3, 4 и D (рисунок 1-а, 2-а). Глубокие уровни = 3 и = 4 имеют характерные максимумы ионизации (T ≈ 235 K) и при этом формируют единственный пик на DLTS-зависимости. В случае построения DLTS-спектра при больших интервалах стробности (рисунок 1-б, 2-б; кривая D), в температурном интервале   (100–275) K образуется

DLTS-зависимость сложной конфигурации, представляющая собой суперпозицию сигналов от четырёх низкотемпературных ГУ ( = 1,2,3,4). При этом главный максимум DLTS-спектра на этом участке совпадает с температурой максимальной ионизации ГУ = 2, а побочный – с температурой характерных максимумов ионизации уровней = 3 и = 4. Изложенные факты косвенным образом подтверждаются и экспериментальными результатами. Оценки, проведённые по реальным DLTS-спектрам, показывают, что в температурном диапазоне ионизации ГУ = 3 и = 4 регистрируется один центр с энергией E = [ E c ( 0,486 ± 0,307 ) ] эВ. Величина абсолютной погрешности оказывается соизмеримой с энергией ионизации глубокоуровневого центра = 3.

В-четвёртых, из результатов численного анализа (рисунки 1, 2) следует, что процесс ионизации ГУ имеет более сложный характер, чем подразумевают стадийные кинетики, упомянутые выше. Например, кинетики, предлагаемые в работах [1–6, 8–10], не в состоянии объяснить существование экстремумов на температурных зависимостях степени ионизации для центров: = 3 и = 4 в диапазоне температур (175–275) K (рисунки 1, 2, зависимости 3, 4); = 1 в диапазоне температур (300–325) K (рисунки 1a, 2b, зависимости 1). Помимо этого, не объясняют они и того факта, что на ГУ = 4 и = 2 (рисунки 1–2, зависимости 4 и 2) при температурах 250 и 350 K соответственно, происходит полная рекомбинация дырок. В то же время, для других ГУ степень ионизации остаётся практически неизменной. Из всего этого следует вывод о том, что в большинстве случаев все стадийные кинетики [1–6] при релаксационной спектроскопии глубокоуровневых центров будут приводить к значительной методологической погрешности в определении параметров этих ГУ. Максимальная же методологическая погрешность будет достигаться при определении концентраций центров, в случае использования кинетики перезарядки ГУ, предложенной в работах [1, 2].

В-пятых, как отмечалось в работе [3], глубокоуровневые центры, лежащие ближе к середине запрещённой зоны полупроводника, из-за эффективного обмена зарядами с обеими разрешёнными зонами, оказывают существенное влияние на характер релаксации ёмкости. В случае арсенида галлия такими центрами являются поверхностные электронные состояния (ПЭС) ( i = 5). Из результатов численного анализа следует, что плотность поверхностных электронных состояний (ПЭС) оказывает существенное влияние в целом на кинетику перезарядки всех ГУ в GaAs. Сравнительный анализ DLTS-зависимостей (D) представленных на рисунках 1a – 2a и 1a – 2b, показывает, что увеличение концентрации ПЭС всего лишь на полпорядка приводит к существенному перераспределению амплитуд всех DLTS-пиков. Поскольку, согласно [1, 2], амплитуда DLTS-пика определяется концентрацией глубокоуровне-вых центров, незначительное увеличение концентрации ПЭС приводит к значительной погрешности в определении концентрации других ГУ. Увеличение же концентрации ПЭС на два порядка приводит к тому, что область «нелинейности» на аррениусовских зависимостях, представленных на рисунке 3b (выделенная область), становится существенно шире, чем такая же область на рисунке 3a.

Кроме того, из сравнительного анализа данных, приведённых в таблице 2, следует, что концентрация ПЭС оказывает влияние и на точность определения энергий ионизации ГУ. Из всего сказанного можно сделать вывод, что