Математическое моделирование энергетического баланса многоцелевого лабораторного модуля на автономном участке полёта

Автономный участок после отделения от ракеты-носителя (РН) до стыковки с орбитальной станцией является наиболее сложным этапом функционирования любого космического объекта — как модуля, так и транспортного корабля. Одной из наиболее актуальных задач на данном этапе является соблюдение баланса электрической энергии (далее — энергобаланса) объекта. До настоящего времени проектный расчёт энергобаланса представляет собой определение разности между приходом и расходом электроэнергии для наихудшего случая светотеневой обстановки на орбите объекта. Однако, такой расчёт неинформативен для целей определения подходящих окон старта изделия.

В настоящей статье представлена методика расчёта энергобаланса космического объекта с момента его предстартовой подготовки (перехода на бортовое питание) до стыковки с орбитальной станцией на примере многоцелевого лабораторного модуля (МЛМ).

Запуск МЛМ был произведён 21.07.2021 г. в 17:58:25, его автономный полёт составил восемь суток. МЛМ успешно пристыковался к Международной космической станции (МКС) 29.07.2021 г. в 16:29:05. В момент написания статьи запуск МЛМ ещё не был произведён. На момент выхода статьи авторы анализируют телеметрическую информацию, а затем будет проведено сравнение прогнозируемых и реальных данных.

Автономный полёт МЛМ начинается после его отделения от третьей ступени РН «Протон-М». Стыковка МЛМ к МКС осуществляется в конце восьмых суток автономного полёта. Расход электроэнергии аккумуляторных батарей (АБ) комплекса энергоснабжения МЛМ начинается с момента перехода на бортовое питание за 10 мин до контакта подъёма РН. Критерием выполнения энергобаланса МЛМ является уровень заряда АБ на момент перевода МЛМ на объединённое питание от МКС. Задача расчёта энергобаланса сводится к определению энергопотребления всех работающих бортовых систем, энергоприхода от солнечных батарей (СБ) с учётом изменяющейся ориентации, уровня запаса электрического заряда АБ для режимов функционирования на этапах предстартовой подготовки, выведения, автономного полёта, причаливания и стыковки [1].

Основные характеристики комплекса энергоснабжения МЛМ:

ёмкость одной АБ 360 А·ч; количество АБ 6 шт.; выходная мощность при ориентации СБ на Солнце 6,79 кВт; выходное напряжение в установившемся режиме 28,5±0,5 В.

Панель СБ создана на основе кремниевых фотоэлектрических преобразователей и разделена на 12 электрически независимых, параллельно работающих генераторов тока. Суммарная площадь двух панелей СБ составляет 56 м2 [2] (рис. 1).

Рис. 1. МЛМ на этапе автономного полёта

Расчётная модель

Главным показателем при расчётах энергобаланса является ёмкость АБ, из которых осуществляется энергоснабжение модуля при нахождении на теневом участке орбиты или при нехватке энергии от СБ. К тому же на этапах предстартовой подготовки и выведения МЛМ необходимо учитывать, что СБ расположены под головным обтекателем, и энергоприход от них отсутствует, соответственно, энергия поступает также от АБ. На освещённых участках электроснабжение бортовых систем и заряд АБ происходит от панелей СБ.

Программный комплекс расчёта энергобаланса (ПКРЭ) МЛМ состоит из четырёх модулей, один из которых реализован в программном обеспечении (ПО) Microsoft Access и представляет собой модуль исходных данных в виде реляционной базы данных, включающей в себя описание групп временных событий, режимов полёта, бортовых систем, состоящих из блоков, приборов, модулей и агрегатов. Сама математическая модель реализована в ПО Mathcad и состоит из трёх основных модулей:

• •    1-й модуль — баллистический.

В нём производится расчёт траектории КА;

• •    2-й модуль — расчёта времени ключевых событий. В этом модуле производится расчёт временных событий, таких как моменты начала витков, моменты входа и выхода из тени Земли, моменты начала и конца зон радиовидимости наземных измерительных пунктов (НИП);

• •    3-й модуль — энергетического расчёта. Здесь рассчитывается энергопотребление бортовых систем, энергоприход от панелей СБ, расход и приход заряда на АБ, и строится суммарная циклограмма энергобаланса.

Модуль 1. Для расчёта траектории космического аппарата (КА) полёт делится на несколько участков: участок выведения РН [3], активный участок с включённым ракетным двигателем КА [4] и пассивный участок с выключенным ракетным двигателем КА [5].

Исходными данными для расчёта траектории участка выведения РН являются стартовая масса каждой ступени в момент пуска двигателей этой ступени, тяга двигательных установок (ДУ), удельный импульс ДУ, продолжительность работы ступени РН. Для активного и пассивного участков полёта исходными данными являются параметры Кеплеровых переходных орбит — время переходного импульса, наклонение, высота апогея, высота перигея, аргумент широты, аргумент перицентра, эксцентриситет, большая полуось.

При расчёте положения КА относительно Земли используются следующие, преобразованные авторами, формулы долготы КА ( λ ) и географической широты ( ϕ ) [6]:

λ = Ω + arctg(cos( i ) ∙ tg( ψ + θ )) + π ∙ m ;

ϕ = arcsin(sin( i ) ∙ sin( ψ + θ )),

Преобразовывая функцию (3) обратно в декартову систему координат, получаем функцию для массива данных по времени координат x , y , z (рис. 2):

x ( t )

у ( ) = f ( i ^ ( t ) v q ⁽ t )) •

где Ω — долгота восходящего узла; i — наклонение орбиты; ψ — аргумент перицентра; θ — значение истинной v + o)

аномалии; m = min           , m e R ;

V 2 п у

cos( λ )     cos( ϕ )

X = r ∙ sin( λ )      cos( ϕ )

sin( ϕ )

где X — декартова координата КА относительно Земли.

Для удобства расчёта проведено преобразование (1) из декартовой системы координат в полярную систему координат. Таким образом, система дифференциальных уравнений движения КА выглядит следующим образом:

.

r = u

1 ^{2 (} t )

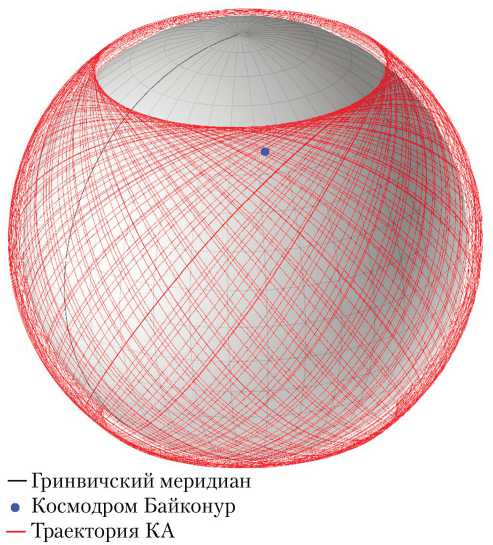
— Гринвичский меридиан • Космодром Байконур — Траектория КА

Рис. 2. Траектория полёта КА

q =

.µ u = ω2∙ r – r 2З + k a∙g0∙n x(t)∙e

ϑ ^. = ω

_.       –2∙ ω ∙ u + k _a ∙ g ₀ ∙ n_x ( t ) ∙ e

ω =

r

где     k_a =

r

,

n

0, если пассивный участок полёта, 1, если активный участок полёта;

g ₀ — ускорение свободного падения на уровне моря; n_x ( t ) — продольная пере-

vr грузка КА; er = V r

u

V

относительная

v n радиальная скорость; en = V

ω r

V

отно-

сительная тангенциальная скорость; μ _З — гравитационный параметр Земли.

Решая дифференциальное уравнение (2) для каждого участка, получаем следующую функцию:

X ( t ) = f ( q , t , Ω ).                            (3)

Модуль 2 . Исходными данными для расчёта моментов начала каждого витка является траектория КА, рассчитанная в Модуле 1 . Специальная программная процедура определяет моменты времени, в которых траектория КА пересекает плоскость экватора с юга на север, таким образом, формируется массив исходных значений — время начала витка.

Входными данными для расчёта моментов видимости НИП являются его координаты: северная широта, восточная долгота, минимальное возвышение луча видимости над горизонтом.

Функция расчёта угла возвышения КА над горизонтом рассчитывается по предложенной авторами формуле:

Г( x ) = –arcsin

^x Н И П ^{∙ ∆ x}

| x | ∙ |Δ x |

,

где x _НИП — координата НИП; x — координата КА; Δ x = x – x _НИП .

Условие расчёта моментов времени входа и выхода из зоны видимости НИП:

γ _i = Г( x ) – γ _min ,

где γ _min — минимальное возвышение луча видимости над горизонтом.

Специальная программная процеду-

ра определяет моменты времени, в которых угол возвышения КА над горизонтом равен минимальному углу возвышения луча видимости НИП над горизонтом. В зависимости от того, возрастает угол возвышения КА или убывает, происходит вход в зону видимости НИП или выход, соответственно (рис. 3).

Для расчёта периодов видимости Солнца исходными данными являются дата и время старта объекта.

Функция расчёта направления на Солнце рассчитывается по предложенной авторами формуле:

( cos( Фс( 0)

d_C( t) = зш(ф_с( t))

cos(X_C( t))^ cos(XC( t))

sin( ф_с( t))

где ϕC(t)) = arcsin(sin(γн) ∙ sin(λC(t))) — широта точки, где Солнце в зените; γн — угол наклона земной оси к эклип тике; λ (t) = 2π ∙ 0 вс + ω ∙ t — теку-C 365,25 Г

щая долгота Солнца относительно точки весеннего равноденствия; d ₀ — дата старта; d _вс — дата весеннего

солнцестояния; ω _Г — угловая скорость движения Земли по орбите;

λ _C ( t ) = –2 π ∙

( T 0.МСК – 3) – 12

– ω _С ∙ t

— текущая

долгота полуденного меридиана; T _0.МСК — время старта; ω _С — скорость суточного вращения Земли относительно Солнца.

Угол возвышения Солнца над видимым горизонтом рассчитывается по предложенной авторами формуле:

α _св ( t ) = arcsin

x^T ∙ d _C ( t ) | x |

+ arccos

R _З | x |

где x^T — транспонированный массив координаты КА; R _З — радиус Земли.

Угол склонения Солнца рассчитывается по предложенной авторами формуле:

β _C = arcsin( d _C ( t ) ^T ∙ ω _орб ),

где ω орб

sin( i ) –sin( i )

sin( Ω )

cos( Ω ) — единичный sin( i )

вектор орбитального вращения КА.

Условие расчёта моментов времени входа и выхода из тени Земли:

sign( α _i ) ≠ sign( α _{i + 1} ).

Специальная программная процедура определяет моменты времени, в которые угол возвышения Солнца над видимым горизонтом при наблюдении с КА меняет знак. Если угол α положительный, то КА выходит из тени Земли, если угол α отрицательный — КА входит в тень Земли (рис. 4).

От ориентации КА зависит угол освещённости СБ. Для удобства расчёта введён коэффициент учёта пологости освещения СБ, характеризующий плотность потока энергии солнечного излучения, пропорционального косинусу угла падения лучей. Угол падения лучей отсчитывается от нормали к поверхности СБ. В программе полёта МЛМ заложено несколько видов ориентации (таблица). Методика расчёта предложена авторами. Точности угловой и координатной ориентации модуля являются параметрами, мало влияющими на адекватность и достоверность результатов.

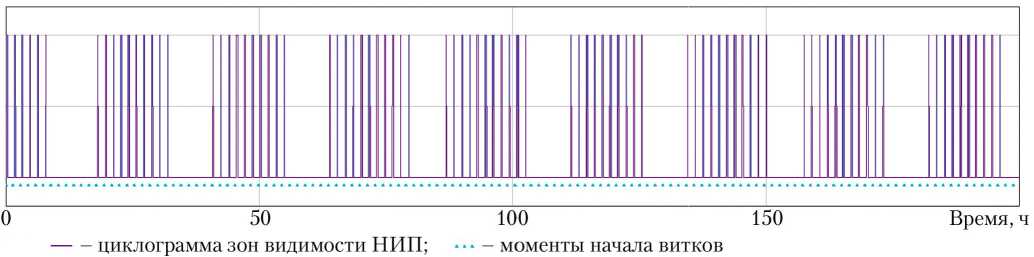
Рис. 3. Циклограмма зон видимости НИП

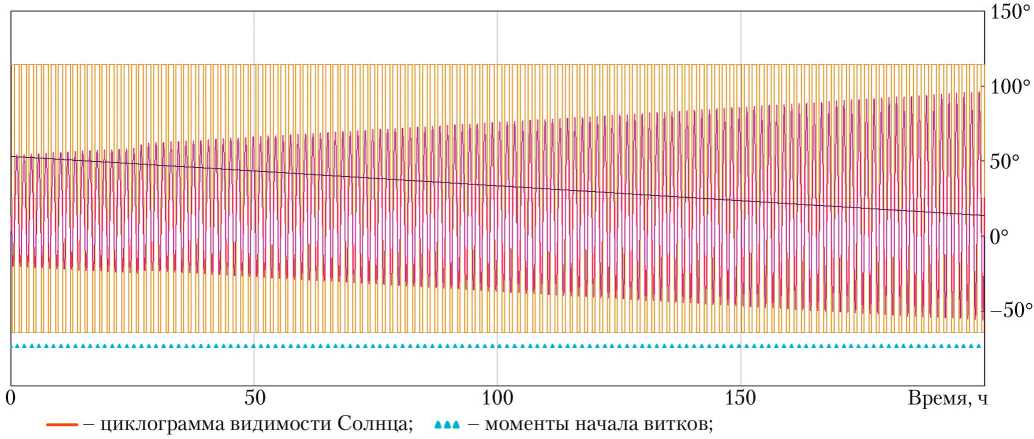
--угол возвышения Солнца над видимым горизонтом; --- - угол склонения Солнца

Рис. 4. Результаты расчёта времени ключевых событий

Коэффициент учёта пологости освещения СБ

Вид ориентации	Коэффициент учёта пологости освещения
«Минус ОСК Р» — ось – X направлена по вектору скорости, ось Z изделия параллельна подстилающей поверхности Земли	/ x ∙ d C cos          , если cos( γ ) < cos( γ ) кр cos( γ осв) =            | x | ∙ | d C | 0, если cos( γ ) > cos( γ кр) k y = kosC . >|
«Закрутка на Солнце» — ось Y изделия направлена на Солнце	ксв = 0 k Y = 1
«Двухосная закрутка» — КА вращается вокруг осей X и Z со скоростью 0,25 ° /с, ось X без возможности выставления на Солнце	sinC^) = d C • F ( t ) k Y = 0,7 (значение является математическим ожиданием)
«Одноосная закрутка 1» — КА вращается вокруг оси Y со скоростью 2,2 ° /с, ось Y направлена на Солнце	У осв = 0 k Y = 1
«Одноосная закрутка 2» — КА вращается вокруг оси Y со скоростью 2,2 ° /с, ось Y изделия направлена по нормали к плоскости орбиты	sin( β ), если cos( γ ) < cos( γ кр) cos( γ ) = осв        0, если cos( γ ) > cos( γ кр) k Y = kosr . >|

Примечание . ж = 1,4 — коэффициент, учитывающий отражение света от поверхности ФЭП и защитного стекла, выбирается в интервале 1...2; у _кр = 70 ° — критический угол падения лучей света, принимаемых датчиками ФЭП; F ( t ) — функция положения СБ.

Таким образом, расчёт энергоприхода от СБ с учётом ориентации КА производится по следующей формуле:

W СБ = 6 790 k _Y .

Модуль 3. При построении итоговой циклограммы энергобаланса рассчитывается уровень заряда АБ с учётом циклограммы электропотребления бортовых систем.

Циклограмма электропотребления бортовых систем заложена в ПО MS Access в виде базы данных, учитывающей моменты включения/выключения приборов и агрегатов и мощности их электропотребления. База данных импортируется в ПО Mathcad , выстраивается массив данных по суммарному электропотреблению бортовых систем в каждый момент времени.

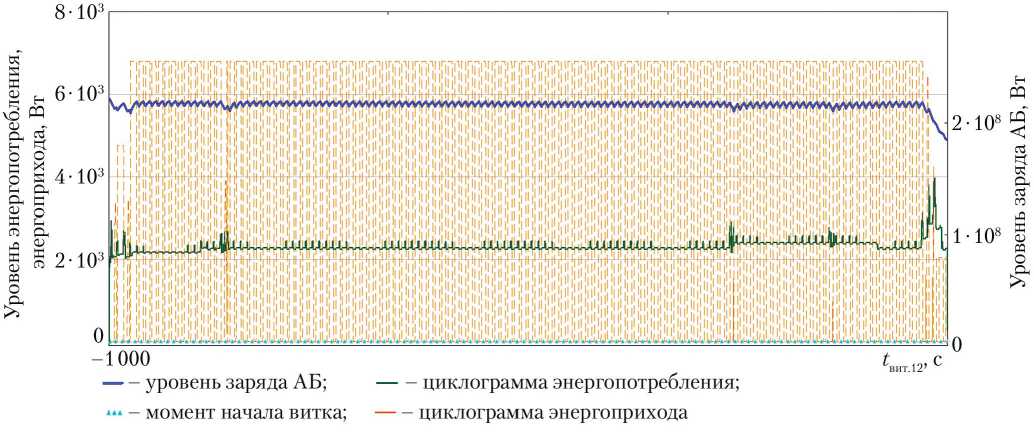
Рис. 5. Циклограмма энергобаланса

Таким образом, уровень заряда АБ определяется следующей системой дифференциальных уравнений, предложенной авторами [7]:

^η АБ ^∙

lim. z ^∙

.

^{Q = Р} АБ ^∙

Q

, если Р _АБ >0

^Q lim

, (4)

, если Р _АБ <0

η зру

lim

где Р _АБ = η _рт ∙ W _СБ – P _Σ — мощность тока на входе в АБ; η _рт — КПД АБ на разряде; P _Σ — суммарная мощность, потребляемая бортовыми системами; η _АБ — КПД АБ на заряде; η _зру — КПД в каналах заряда/разряда; k _{lim. z} ( x ) — функция ограничения заряда; k _{lim. r} ( x ) — функция ограничения разряда; Q — уровень заряда АБ; Q _lim — максимальный уровень заряда АБ.

В результате решения дифференциального уравнения (4) строится циклограмма энергобаланса объекта (в данном случае МЛМ) с момента перехода на бортовое питание в процессе предстартовой подготовки до подключения к объединённому питанию Российского сегмента МКС (рис. 5).

Результаты работы

В результате проведённой работы создана математическая модель расчёта энергобаланса из ПКРЭ, позволяющая в автоматизированном режиме с высокой

точностью определять необходимые характеристики систем энергоснабжения при проектировании изделий космической техники.

В настоящее время авторы проводят анализ большого объёма телеметрической информации, по результатам которого будет верифицирована описанная математическая модель. Сравнительный анализ расчётных и фактических значений энергобаланса МЛМ за время его автономного полёта планируется к публикации.