Математическое моделирование эволюции сферического клеточного агрегата в вязком матриксе. Формирование клеточных структур

RUSSIAN JOURNAL OF BIOMECHANICS

Развитию различных биологических тканей и органов в живых организмах зачастую предшествует организация клеток в агрегаты, окруженные внеклеточным матриксом. Дальнейшее развитие клеточных агрегатов при- водит к формированию различных клеточных структур. В частности, формирование новой сети кровеносных сосудов при кластерном васкулогенезе, имеющим место в условиях гипоксии, проходит стадию агрегации клеток-предшественников с последующим образованием просвета и слияния с ранее существовавшей сосудистой се-

се) ® ®

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

тью [1]. Формированию полости в раннем эмбриональном развитии лягушки Xenopus Laevis также предшествует рыхлое скопление клеток [2; 3]. В качестве другого пути развития можно привести пример роста опухолей, характеризуемого существованием плотной основной массы клеток и инвазией отдельных групп клеток в окружающие ткани [4; 5]. Клеточные агрегаты, полученные в искусственных условиях, являются объектом изучения влияния активных взаимодействий клеток со своим окружением [6; 7].

Выбор пути развития определяется самыми разными факторами. В настоящее время существуют многочисленные данные, указывающие на то, что механические свойства внеклеточного матрикса играют значительную роль в организации клеточных структур в биологических тканях [8; 9]. Известно, что вязкоупругие свойства матрикса регулируют поведение одиночной клетки на плоском субстрате, однако влияние, в частности, вязких свойств матрикса на коллективную динамику клеток в тканях является предметом обсуждений. Следует отметить важную роль механических активных взаимосвязей, которые развиваются клетками при взаимодействии с матриксом.

Теоретические исследования, в которых методы механики сплошных сред использовались для моделирования развития клеточных сфероидов, в первую очередь связаны с ростом опухолей. Основной круг задач включает в себя описание развития неоднородности в опухолевых сфероидах, определяемой различной доступностью питательных веществ в разных областях сфероида и развитием напряжений в результате деления клеток. Рассматриваются задачи, связанные с распространением сфероида в окружающие ткани в результате ростовых процессов и взаимодействия с окружающим тканями. Предметом обсуждений являются законы роста, учитывающие взаимосвязь скорости деления клеток с напряженным состоянием среды. Математическое моделирование клеточных систем с учетом различных биологических и физических механизмов, принимающих участие в развитии клеточных агрегатов, представлено огромным количеством работ, которые различаются методами моделирования и детализацией описания процессов. Ниже приведены ссылки на небольшое количество публикаций, в которых присутствуют более полные обзоры существующих моделей.

Задача о распространении плоского фронта опухолевых клеток в недеформируемом матриксе рассматривалась в [10; 11]. Эволюция концентрации клеток описывалась уравнением неразрывности с учетом деления клеток. Поток плотности определялся эмпирическим соотношением, учитывающим, помимо диффузии, соответствующей случайным клеточным блужданиям, также активные нелокальные составляющие, определяемые активными взаимодействиями клеток между собой и матриксом. В основу модели положена аналогия между движением клеточной среды и фильтрационным течением жидкости, однако используемые при этом гипотезы справедливы только для очень разреженных клеточных сред.

В [12] представлена модель развития радиальной неоднородности клеточных сфероидов, характеризуемой различием свойств клеток. Формирование некротического ядра и областей с различной пролиферативной активностью клеток связано с неоднородностью распределения питательных веществ, которая описывается уравнением диффузии. Влияние механических параметров среды на развитие клеточных агрегатов не обсуждается. Обратная связь между скоростью роста и напряженным состоянием агрегата, контролируемая также доступностью питательных веществ, учитывается в [13], где клеточный агрегат рассматривается как пороупругое растущее тело. Этот класс моделей более подробно обсуждается в [14; 15]. Однако, несомненно, существенные механизмы активных взаимодействий клеток между собой и матриксом в этих моделях не рассматриваются.

В другой группе моделей [16–18] используются методы механики многофазных сплошных сред, которые учитывают присутствие активных механических взаимодействий клеток между собой и матриксом в процессе развития аваскулярных опухолей, а также зависимость скорости пролиферации клеток от напряжений, концентрации клеточной фазы и питательных веществ. Включение сократительных элементов в клеточную фазу позволило учесть влияние активных напряжений на процесс клеточных переупаковок, рассматриваемых как вязкое течение. Активные механические напряжения, создаваемые клетками, учитывались посредством немонотонной зависимости давления в клеточной фазе от ее объемной концентрации. Широкий обзор математических моделей, описывающих различные проявления роста аваску-лярных опухолей, представлен в статье [19]. Особое внимание уделяется роли механических взаимодействий опухолей с окружающим тканями.

Основные принципы построения континуальных моделей биологических сред, проявляющих механическую активность, были предложены в [20]. В работе представлены характеристики, позволяющие учитывать общие активные свойства клеточной среды и обсуждаются возможные механизмы, описываемые этими характеристиками. Предлагается введение вспомогательных фаз, которые соответствуют механически активным субклеточным элементам, связанным с созданием активных напряжений, контролирующим переупаковку клеток. Эта работа послужила основой построения континуальной модели биологической среды, образованной двумя активно взаимодействующими клеточными фазами и жидкостью [21], которая использовалась в задаче о сортировке двух типов клеток [22; 23] и образования полых структур [24; 25] в клеточных агрегатах.

В данной работе представлено теоретическое исследование системы «клетки – матрикс» как механической системы, исключая из рассмотрения эффекты, связанные с делением клеток и выработкой протеолитических ферментов. Будет исследовано влияние активных взаимодействий клеток как между собой, так и вязким матриксом, а также начального состава клеточного агрегата на процесс перераспределения объемных концентраций клеток и матрикса при развитии клеточных структур.

Постановка задачи и метод решения

Континуальная многофазная модель

Рассмотрим клеточный агрегат, образованный клетками и внеклеточным матриксом. В начальный момент времени агрегат имеет сферическую форму и окружен матриксом (рис. 1). Область, занятая агрегатом (совместно клетками и матриксом), в начальный момент времени ограничена сферой радиуса R , а область пространства, в которой присутствует только матрикс, считается неограниченной. Неограниченная область пространства, занятая матриксом, моделируется сферой большого постоянного радиуса R . В среде также присутствует внеклеточная жидкость.

Постановка задачи о перераспределении объемных концентраций клеток и матрикса будет использовать континуальную модель биологической многофазной среды, образованной двумя активно взаимодействующими твердыми фазами и жидкостью, разработанную в [5]. В данной задаче одна из твердых фаз образована клетками, а другая – внеклеточным матриксом. Истинные плотности фаз будем считать постоянными и равными между собой. Биологические особенности рассматриваемых фаз вносят некоторые отличия от [5]. Одним из них является отсутствие активных взаимодействий в фазе матрикса. Другое отличие состоит в изменении определяющих соотношений для активных механических взаимодействий между клетками и матриксом, которое в данном случае учитывает нелокальную стягивающую составляющую в этих взаимодействиях.

Все уравнения написаны в физическом базисе сферической системы координат с началом в центре сферы. Ниже приведены основные предположения, используемые в постановке задачи.

В уравнениях импульсов будем пренебрегать составляющей сил межфазного взаимодействия твердых фаз с жидкостью, которая обусловлена вязким трением. Оценки числовых значений соответствующих безразмерных параметров выполнены в [21; 28]. Эти оценки позволяют также пренебречь изменением гидростатического давления во внеклеточной жидкости, считая его равным нулю во всей занятой матриксом области (предполагается свободное перетекание жидкости через границу клеточного агрегата), и решать уравнения для клеточной фазы и матрикса отдельно от уравнений, описывающих движение жидкости. Уравнения, описывающие движения жидкости, далее не рассматриваются.

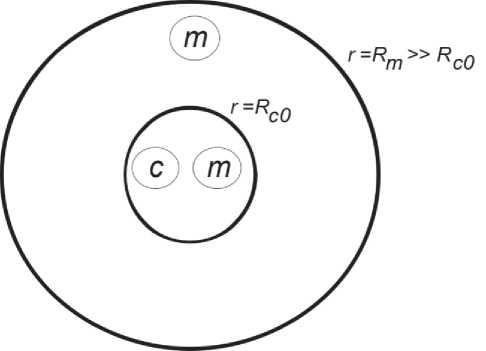
Рис. 1. Схематическое изображение клеточного агрегата, окруженного матриксом, в начальный момент времени. Буквенные обозначения c и m , обведенные маленькими кругами, обозначают присутствие клеток и матрикса в разных областях. Координата r = R_c0 является радиусом сферы, ограничивающей клетки, сфера радиуса R_m = const ограничивает матрикс

Активные механические взаимодействия клеток между собой и внеклеточным матриксом играют ключевую роль во многих биологических процессах, связанных с миграцией клеток и формированием тканей и органов. Развитие активных взаимодействий обеспечивается такими фундаментальными механизмами, как адгезия и сократимость клеточного скелета. Специфические поверхностные белки адгезии обеспечивают прочное сцепление участков клеточных поверхностей как между собой, так и с волокнами матрикса. Активная перестройка клеточного скелета и действие моторных белков генерирует силу, которая действует на соседние клетки и окружающий матрикс. В процессе взаимодействия с матриксом клетки образуют псевдоподии – выросты клеточной мембраны, которые устанавливают прочные контакты с волокнами матрикса [26; 27]. Активные механические взаимодействия между клетками и матриксом возникают под воздействием сократительных сил, развиваемых элементами клеточного скелета, расположенными в псевдоподиях. Активные силовые взаимодействия между клетками развиваются в результате более разнообразных проявлений механизмов адгезии и сократимости цитоскелета в зависимости от типа клеток и тканей (кратко изложено во введении [23]).

Описание активных взаимодействий клеток со своим окружением может быть выполнено путем введения вспомогательных фаз, отождествляемых с теми клеточными структурами, в которых развиваются активные силы взаимодействия [20].

Введем две вспомогательные фазы, первая из которых обеспечивает активные нелокальные взаимодействия между клетками и характеризуется тензором напряжений т(c). Вторая вспомогательная фаза с тензо- ром напряжений Тcm] = т(cm) + т(mc) обеспечивает нелокальные перекрестные активные взаимодействия между клеточной фазой и матриксом. Составляющие т(cm) и т( mc) перекрестного тензора напряжений описывают активные нелокальные взаимодействия между частицей клеточной фазы, находящейся в рассматриваемой точке, и матриксом, а также частицей матрикса в рассматриваемой точке и клеточной фазой соответственно. Объемы, занимаемые дополнительными фазами, считаются пренебрежимо малыми в сравнении с объемами основных фаз. Напряжения в клеточной фазе и фазе матрикса характеризуются тензорами a' c) и ст'm).

Уравнения импульсов для клеточной фазы и матрикса, пренебрегая инерционными эффектами, примем в следующем виде:

ризует эффективное расстояние, на котором происходит силовое взаимодействие клеток со своим окружением и имеет порядок одного или нескольких клеточных размеров.

В исследовании [3] использовалось предположение, что активные стягивающие взаимодействия развиваются только между клетками внутри фазы, а в перекрестных взаимодействиях учитывалась только расталкивающая составляющая. В данном случае составляющие т ' ^cm ) и т ^{( mc} ) перекрестного тензора напряжений будут учитывать нелокальные стягивающие силы, действующие в данной точке на частицу одной фазы со стороны удаленных на определенное расстояние частиц другой фазы. Определяющие соотношения для активных напряжений примем в следующем виде:

V- ( Ф_со ⁽ c ) + т ⁽ c ) + т ⁽ cm ) ) + F = 0, V- ( Ф_ио ^{( m} ) + т ^{( m} ) + т ^{( mc} ) ) - F = 0.

т(с’ = -Пс -1 + mc —^-— -ФС[ФС- N0 Nds, с       с 4п^2 с с sS

Здесь F – сила межфазного взаимодействия между клеточной фазой и матриксом, ф_с и ф_т — объемные концентрации клеточной фазы и матрикса соответственно. Второе и третье слагаемые в скобках учитывают силы взаимодействия с вспомогательными фазами.

Выражение для силы межфазного взаимодействия F , полученное в работе [5], имеет следующий вид:

т(cm’ = -Пcm -1 + mcm       - Ф JФm ■ N ® Nds,

^{4 п} R s    S

Т ^{( mc} ’ =-П cm - 1 + m cm ,' -Ф m ( Ф с ■ N ® N ds , ^{4 п} R s     S

П с

Ф ²

E ---^Ф---,

1 -Ф с -Ф m

^П cm

=E cm

ФФ cm

1 -Ф c -Ф m

F =Ф mPc V

ф 1

6 +ф J

\ т с т т /

Ф cPm V

Фт 1 + Uс +Фт J

+ Кт Ф с Ф т ( V ' m ’ — V ' c ) ), P c =- 1 1 . ( a ' ^с ) ), P m =- j I . ' a ' ^m ) ).

Здесь v ' c ) и v ^{( m} ) - векторы скорости клеточной фазы и матрикса, I [ ( o ' ^с ) ) и I До ' ^m ) ) - первые инварианты тензоров напряжений в твердых фазах. Выражение (2) учитывает две составляющие силы межфазного взаимодействия, одна из которых связана с действием сил давления (первое и второе слагаемое), вторая – с силой вязкого трения на межфазных поверхностях.

Определяющие соотношения для активных напряжений в дополнительных фазах учитывают различные проявления активности клеток при взаимодействии со своим окружением: хаотическую активность при взаимодействии между собой и с матриксом, которая характеризуется давлениями П с ( Ф _c , Ф _m ), П cm ( Ф _с , Ф _m ) и проявляются в отталкивании частиц соответствующих фаз, а также и нелокальные стягивающие усилия, направленно реагирующие на неоднородность их микроокружения. Стягивающие составляющие определяются неоднородностью распределения соседних клеток или матрикса по сферической поверхности некоторого фиксированного для данной среды радиуса R (радиуса дальнодействия) с центром в рассматриваемой точке. Этот радиус характе-

Здесь I – единичный тензор. Интегрирование выполняется по сферической поверхности S фиксированного радиуса R с центром в рассматриваемой точке, N – единичный вектор нормали к поверхности сферы. Если интегрирование производится по той части поверхности, на которой подынтегральная функция не определена, то в этих точках она доопределяется нулем.

В общем случае тензоры скоростей деформации твердых фаз можно представить в виде суммы составляющих, связанных как с деформацией клеток и волокон матрикса (для них может быть принят один из законов упругости), так и с их переупаковкой [28]. В данной работе примем гипотезу о малости первой составляющей по сравнению со скоростью неупругого деформирования, связанного с переупаковками частиц фаз. Будем рассматривать неупругое деформирование фаз как течение, которым управляют активные напряжения и напряжения в фазах. Выражения для тензоров скоростей деформации e ' ^с ) и е ' ^m ) клеточной фазы и матрикса соответственно примем в следующем виде:

е ' ^с >  =    ¹    (о ' ^с )

2щ (

—

__' m ) т^О )

)—— т ' ^с ) ² М 11

—

¹    т ' cm )

2 И 12

e

,( ^m ) =

= — ( о ' ^m ) 2ц₂^V

—

Ф с о ' ^с ’

—

т ' ^mc ) ) .

Выбор знаков учитывает, что растягивающие напряжения во вспомогательных фазах стимулируют сближение частиц фаз, а растягивающие напряжения в

рассматриваемой фазе и сжимающие напряжения в соседней фазе этому уплотнению препятствуют.

Предполагается, что в среде отсутствуют деление и гибель клеток, а также потоки массы между твердыми фазами и жидкостью. Тогда уравнения неразрывности для клеточной фазы и матрикса примут следующий вид:

+ V- (Ф cv(c)) = 0, d t                                      (5)

^ + ?• (Ф m V(m)) = 0.

d t

Система уравнений дополняется кинематическими соотношениями для компонент тензоров скоростей деформации твердых фаз:

e ^{( c} * = 0,5( V v ^{( c} * + ( V v ⁽ c ) ) T ),

(6) e ^{( m} ) = 0,5( V v ⁽ m ) + ( V v ⁽ m ) ) T ).

Уравнения (1)–(6) будут использованы для исследования эволюции перераспределения объемных концентраций клеток и матрикса в клеточном агрегате. Решение задачи будет выполнено в предположении сферической симметрии. У всех тензоров смешанные компоненты считаются равными нулю, а векторы скоростей будут иметь единственную отличную от нуля компоненту в радиальном направлении.

Граничные и начальные условия

Граничные условия учитывают независимое перемещения поверхности, ограничивающей клеточную фазу. Условие сферической симметрии обеспечивает сохранение сферической формы клеточного агрегата, и r = R_c (t ) является уравнением его границы.

Скорость матрикса на удаленной внешней границе считается равной нулю, и в качестве условия при r = Rm примем, что vm) = 0.                          (7)

Граница клеточной фазы r = R_c ( t ) является поверхностью разрыва для фазы матрикса. На этой границе должны быть сформулированы условие непрерывности потока массы матрикса и условия, учитывающие перераспределение нагрузки между твердыми фазами.

Условие непрерывности потока массы матрикса при r = R_c tt ) имеет вид:

[Ф m ( V m — R c ) ] = 0.                  (8)

Квадратные скобки обозначают разность соответственных величин по разные стороны разрыва, точкой обозначена производная по времени.

Условия для напряжений, учитывающие перераспределение нагрузки в результате силового взаимодействия частиц клеточной фазы и матрикса по разные стороны от разрыва, были предложены в [29]. Они имеют следующий вид:

ф c ^ rc ) +т : ) ■: ) =- p ’ф - Ф m ,

[ф m e ) +€ ) +e ) ]=- p *ф - Ф т ,        (9)

_n * ₌ P^m — P⁺m^фc' ^p =    ф ; +Ф m   '

Здесь p * является средним давлением на поверхности межфазного контакта при r = R_c (t ) . Верхний индекс «плюс» или «минус» указывает на значение соответствующей величины справа или слева от разрыва.

Перемещение границы r = R_c (t ) определяется движением клеточной фазы, поэтому при r = R_c (t ) считается выполненным условие

R c ( t ) = v rc ) .                        (10)

Из уравнений неразрывности (5) и условия ограниченности скоростей фаз в центре сферы следует, что при r = 0 :

v ( c >  = v ( ^m ) = 0.                      (11)

Граничные условия для объемных концентраций фаз не ставятся, так как их границы являются характеристиками уравнений (5). Соответствующие граничные условия получаются из решения уравнений (5), записанных в граничных точках.

В начальный момент времени будем задавать положение границы клеточной фазы R_c (0) = R_c0 и начальные распределения концентраций фаз ф_с (0, r ) = ф.₀ ( r ), ^Ф m ^(0, r ) = ^Ф m 0⁽ r ) .

Метод решения

Преобразуем систему уравнений (1)–(6), выразив тензоры напряжений для твердых фаз из уравнений (4) и подставив их в уравнения равновесия (1), используя (6). В области r <  R_c (t ), занятой клеточным агрегатом, будут получены два уравнения второго порядка по r для единственной ненулевой радиальной компоненты векторов скорости клеточной фазы и фазы матрикса. Остальные уравнения равновесия будут выполнены тождественно в силу сферической симметрии задачи. Уравнение для радиальной компоненты вектора скорости матрикса в области R_c (t ) <  r <  R_m получается аналогично. При этом следует учитывать, что в этой области ф_с = 0, v ^{( c} ) = 0 и q ' c ) = т ⁽ c ) = т ^{( cm} ) = 0 . Полная система уравнений для нахождения ф_с, ф_т и v ^^c ) , v r^m ) будет получена добавлением уравнений неразрывности (5).

Численное решение системы уравнений начинается с уравнений для v(c) и v(m), при этом значения фс и фт берутся с предыдущего шага по времени. Затем при найденных скоростях решаются уравнения (5) для фс, фш, и схема повторяется.

Для решения краевых задач для v^{( c} ) и v ⁽ m ) во внутренней области r <  R_c tt ) , где присутствуют обе твердые фазы, и только для v ⁽ m ) во внешней области R_c (t ) <  r <  R_m , в которой присутствует только матрикс, требуется шесть граничных условий. К их числу относятся условия (11), (8), оба условия (9) и условие (7).

Сложность задачи (помимо подвижности границы клеточной фазы) связана с тем, что во внутренней области присутствуют обе твердые фазы, в то время как во внешней области только одна, а на границе областей (при r = R_c (t ) ) используются условия на разрыве, которые связывают значения скоростей и концентраций фаз по разные стороны разрыва.

Решение уравнения для нахождения скорости фазы матрикса во внешней области ищется методом суперпозиции в виде линейной комбинации двух функций, для которых заданы «начальные» условия на внешней границе r = R_m [30]. Значение множителя в линейной комбинации определяется из условия непрерывности потока массы матрикса (8) на границе r = R c ( t ) . Это позволяет далее вычислить скорости фаз во внутренней области, используя граничные условия (11) и (9), которые будут содержать значение скорости матрикса только во внутренней области.

При расчете скоростей на отрезке [0; R_c ( t )] вводится безразмерная координата ^ = r / R_c ( t ) , что позволяет перейти от решения уравнений с подвижной верхней границей к решению уравнений на отрезке [0; 1].

Разностные схемы решения уравнений для v ⁽ c ) и v ^{( m} ' были получены интегро-интерполяционным методом [31]. Решение разностных уравнений во внутренней области было выполнено методом матричной прогонки. Для численного решения уравнений (5) для ф_с, ф_т использовалась TVD -схема Хартена [32; 33]. Вычисление интегралов в выражениях для активных напряжений выполнено с помощью пятиточечной квадратуры Гаусса [34], при этом учитывается различие пределов интегрирования для внутренних и граничных точек среды, то есть точек, удаленных от границы на расстояние, не превышающее R .

Числовые значения параметров

Введем безразмерные величины:

D*_ ^Rs    F*  _ E cm    * _ P 1    * _^ц 2   ..* _ Р 12

Rs    D , Ecm     77, ^1        , ^2        , ц12

Rc 0         EC        ц        цц

•   m_c     *    m_cm   ,*     kcm^Rc 02

m_c = -c , m cm = -^ , k cm = ——

EC        ECP

.

Здесь ц - характерное значение группы коэффициентов. Введение безразмерных неизвестных выполнено с использованием масштаба времени ц/ Е_с , масштаба длины R и величины E в качестве масштаба для неизвестных, имеющих размерность напряжений.

Свойства системы будут исследованы в зависимости от значений безразмерных параметров, полученных на основе значений размерных величин, характерных для различных биологических сред.

Размер клеточных агрегатов, в которых проявляются различные структурные особенности, могут значительно варьироваться. Так, диаметр зародыша лягушки Xenopus Laevis на стадии, когда визуализируется образование первичной полости в рыхлом клеточном агрегате, составляет около 1,2-1,4 мм [2; 3]. Характерный размер кластеров клеток, образующихся при кластерном васку-логенезе, достигают величины порядка 400 мкм [1]. Изучение сортировки клеток разных тканей проводилось с использованием клеточных агрегатов размером 200500 мкм [6; 7]. Экспериментальное исследование закономерностей роста опухолей проводилось в [4] со сфероидами диаметром 200-600 мкм. Нарушение однородной структуры опухолевого агрегата, связанной с гибелью клеток и появлением некротического ядра, происходит в агрегатах, радиус которых превышает 200 мкм [35].

В дальнейшем примем, что R_c^ = 250 мкм. Последующие расчеты показали, что в качестве радиуса сферы, ограничивающей матрикс, достаточно принять R_m = 5 R_{c 0}. Для радиуса дальнодействия будет использовано значение R_s = 6,25 мкм, превышающее среднее значение радиуса клеток в [1] на 25 % .

Характерные значения коэффициента вязкости клеточной среды для эмбриональных тканей составляют 10 ⁴ ^ 10 ⁶ Па^с [36-38]. В дальнейшем примем ц = 8 • 10⁵ Па^с в качестве характерного значения.

Оценка коэффициента межфазного трения между клеточной фазой и матриксом, выполненная в [39], дает значение 1,8 - 10¹⁴ Паю^м^-2. В дальнейшем используется значение k_cm = 1,8 - 10¹⁴ Паю^м^-2.

Измерения в [24] показали, что клетки при взаимодействии с матриксом генерируют активные силы в диапазоне 10-200 нН в расчете на одну клетку. В [41] было показано, что активные силы, действующие со стороны клеток на матрикс, не превышают 100 нН. Если принять средний размер клетки ~10 мкм [1], то на единицу площади приходится -1010 клеток, и величина активных напряжений, отнесенных к единице поверхности среды , составит 100-2000 Па. Таким образом, получаем оценку коэффициентов m и m , которые характеризуют стяги- вающие составляющие активных напряжений в (3). В дальнейшем используются значения mc = 0,8 кПа и mcm = 1,5 кПа.

В настоящее время отсутствуют экспериментальные данные, позволяющие получить оценки параметров E и E . Рассмотрим состояние равновесия бесконечной ненагруженной сплошной среды, образованной только клетками, объемная концентрация которых является пространственно-однородной. Концентрация клеток будет определяться условием т(c) = 0 . Если принять, что пористость среды составляет 10-30 %, то получим оценку 0,1 < Ec / тс < 0,3 . Примем, что Ес = 0,1 кПа и Ecm = 0,05 кПа.

В дальнейшем звездочку при безразмерных параметрах будем опускать. В расчетах, если не сказано иначе, будут использоваться следующий базовый набор значения безразмерных параметров:

R 0 = 1; R m 0 = 5 ; R_s = 0,025; т _с = 8 ; m_C m = 15; E = 1;

E cm = ⁰’⁵ ; 0 1 = ¹; М- 2 = ¹⁰ ; М 11 = М 12 = ¹ ; k cm = 7,^{8 .}

Числовые значения параметров учитывают, что матрикс является значительно более вязкой средой, чем клеточная фаза.

Результаты расчетов и обсуждение

Исследуем эволюцию объемных концентраций клеток и матрикса в клеточных агрегатах, различающихся начальным составом и активными взаимодействиями клеток между собой и c матриксом. Будут рассмотрены два случая, когда стягивающие активные взаимодействия клеток между собой сильнее или слабее перекрестных взаимодействий клеток с матриксом. В каждом из этих случаев будет рассмотрена эволюция рыхлых и плотных агрегатов, имеющих различный состав.

Последующие расчеты продемонстрировали быстрое уплотнение агрегатов и уменьшение их радиуса на начальном этапе во всех рассмотренных ниже случаях. Плотность агрегата в начальный момент времени будем характеризовать величиной уменьшения его радиуса вследствие быстрого начального уплотнения клеточной фазы. Клеточный агрегат будем называть рыхлым, если начальное уменьшение радиуса агрегата значительно превышает радиус дальнодействия R и плотным, если начальное уменьшение радиуса не превышает R . Степень уплотнения агрегата определяется как его составом, так и активными взаимодействиями клеток между собой и с матриксом.

Рассмотрение эволюции рыхлых и плотных агрегатов связано с различиями их происхождения. В одних случаях агрегаты первоначально формируются, напри- мер, в результате самоорганизации редко расположенных клеток. При этом клетки могут вырабатывать ферменты, разрушающие матрикс. Для этих случаев характерно формирование рыхлой клеточной массы, погруженной в матрикс, объемная концентрация которого в области, занимаемой совместно с клетками, может быть неоднородной. Такой сценарий реализуется, например, при кластерном васкулогенезе [1].

Для рыхлых клеточных агрегатов примем пространственно-однородное начальное распределение клеточной фазы в занимаемой ей области: ф. (0, r ) = ф_с0 при r <  1. Начальное распределение концентрации матрикса имеет вид сглаженной ступени ф m (0, r ) =Ф m 0 + ( Ф m 0 -Ф m 0 ) н s ( r - 1) , где н . ( r ) ^- сглаженная функция Хевисайда, заданная формулой:

0,                    r < -£

H ( r ) = < r +^ + — sin ( п r / s ) , | r | <£ ,   £ = 0,2 .

^£          2 e    2п    ^x

1,

r > £

Здесь фт0 и ф+0 - начальные значения концентрации матрикса в агрегате и на бесконечности.

В других случаях формирование более плотных агрегатов, характерных для роста опухолей, может происходить в результате клеточных делений из небольшой компактной группы клеток. Содержание матрикса в этих агрегатах невелико, и будем считать его постоянным в области, занятой клетками. В этих случаях начальное распределение концентрации матрикса принято в следующем виде: ф m (0, r ) =Ф m 0 + ( Ф m 0 -Ф m 0 ) н £ ( r - 1 -£ ) , где £= 0,05. Начальное распределение клеточной фазы предполагается таким же, как и в рыхлых агрегатах.

• 1.    Доминирование стягивающих активных взаимодействий в клеточной фазе над перекрестными взаимодействиями ( m_c >  m_{c ш}, m_c = 8 и m_cm = 3 ). В случае доминирования стягивающих активных взаимодействий в клеточной фазе над перекрестными взаимодействиями численные расчеты показали сходную эволюцию концентрации клеточной фазы и матрикса как в рыхлых, так и в плотных агрегатах. Начальная стадия быстрого уплотнения сменяется медленным процессом дальнейшего роста концентрации клеточной фазы, перемещением матрикса на периферию и уменьшением радиуса клеточного агрегата. Такой тип эволюции клеточного агрегата можно охарактеризовать как неинвазивное развитие.

• 2.    Доминирование перекрестных активных взаимодействий над межклеточными ( m_cm >  m_c , здесь и далее используется базовый набор параметров). Увеличение перекрестных взаимодействий между клетками и матриксом приводит к изменению сценария эволюции концентрации клеточной фазы и формированию клеточных структур, отличных от простого уплотнения.

  

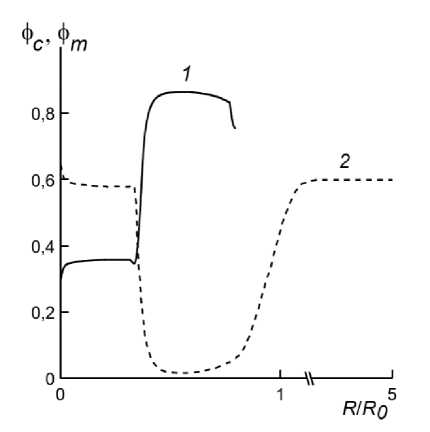
  Рис. 2. Распределения концентраций клеточной фазы и матрикса ( 1 и 2 для ф_с и ф_я, соответственно) в момент времени t = 4,5 при начальных условиях ф c о = 0,4, ф _т о = 0,05 и ф ^ ₀ = 0,6

  
  
  

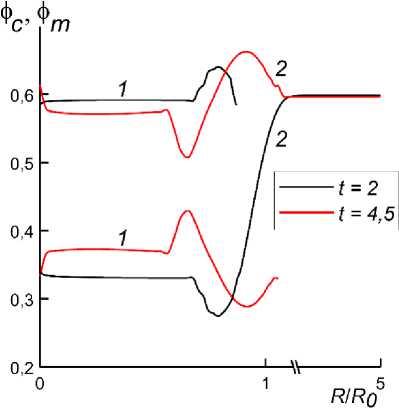
  Рис. 3. Распределения концентраций клеточной фазы и матрикса ( 1 и 2 для ф_с и ф_я, соответственно) в моменты времени t = 2 и t = 4,5 при начальных условиях ф c 0 = 0,4, ф _т 0 = 0,2 и ф т 0 = 0,6

  
  

A. Эволюция рыхлых клеточных агрегатов. Распределения концентраций клеточной фазы и фазы матрикса в момент времени t = 4,5 при ф_с0 = 0,4, ф_т0 = 0,05 и Ф+о = 0,6 показаны на рис. 2. При этих начальных значениях концентраций фаз уменьшение радиуса клеточного агрегата в результате начального уплотнения значительно превышает R и составляет приблизительно 8,5 • R_s . Последующее заполнение освободившегося пространства матриксом сопровождается его втягиванием в область, занятую клетками в результате доминирования сократительной составляющей в перекрестных активных взаимодействиях над межклеточными. Это способствует вытеснению клеточной фазы в радиальном направлении в сторону внешней границы фазы и формированию распределения концентрации клеточной фазы, которое можно рассматривать как начальную стадию формирования полости. Радиус клеточного агрегата незначительно растет. Обрыв кривой 1 (рис. 2) соответствует границе области, занятой клеточной фазой.

Дальнейшее развитие полости требует участия дополнительных механизмов, таких как повышенное гидростатическое давление и ферментативное разрушение матрикса. Исследование участия этих механизмов в рамках используемой модели выполнено в [25].

Влияние увеличения концентрации матрикса в агрегате. Увеличение концентрации матрикса в агрегате влияет на его уплотнение и приводит к уменьшению смещения границы клеточной фазы к центру, в область с меньшим содержанием матрикса. Это способствует меньшему ослаблению перекрестных взаимодействий между клетками и окружающим матриксом.

Распределения концентраций клеточной фазы и фазы матрикса в моменты времени t = 2 и t = 4,5 при ф _{c 0} = 0,4 , ф _т 0 = 0,2 и ф т 0 = 0,6 показано на рис. 3. Начальное уменьшение радиуса агрегата в данном случае составляет приблизительно 7 • R_s .

Главным отличием от предыдущего случая является поддержание более сильных перекрестных взаимодействий в окрестности границы клеточного агрегата. Расчеты показали, что при данных начальных условиях, характеризуемых увеличением содержания матрикса в рыхлом агрегате, в эволюции концентрации клеточной фазы можно выделить несколько стадий. На начальном этапе, как и в предыдущем случае, начинает формироваться неоднородность распределения фазы, которая при определенных условиях может развиться в полую клеточную структуру. На более позднем этапе происходит внедрение небольшой части клеточной фазы в окружающий матрикс. Этот процесс можно рассматривать как проявление инвазивного развития, в котором небольшая группа клеток проявляет тенденцию отделиться от основной клеточной массы.

Влияние концентрации матрикса, окружающего клеточный агрегат. Распределения концентрации клеточной фазы в момент времени t = 4,5 при ф_с0 = 0,4 , ф_т0 = 0,2 и различных концентрациях окружающего матрикса ф +₀ показаны на рис. 4. Расчеты показали, что при малой ф +₀ происходит медленное распространение фронта клеток (кривая 1 ), ограничивающего внутреннее пространство, в котором концентрация клеточной фазы меньше. Увеличение ф+₀ приводит к формированию структуры, имеющей тенденцию к формированию плато, окруженного

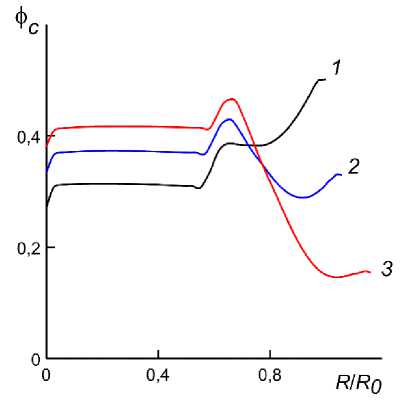
Рис. 4. Распределения концентраций клеточной фазы в момент времени t = 4,5 при ф_с0 = 0,4, ф-₀ = 0,2 и различных ф+₀ . Кривая 1 - ф+₀ = 0,4,

2 — ф⁺ _т о = 0,6, з — Ф т о = о,8

слоем клеточной фазы, и быстрого внедрения небольшой группы клеток в окружающий матрикс (кривые 2 и 3 ).

Из расчетов следует, что инвазии клеточной фазы способствуют более высокие значения концентрации окружающего матрикса, поскольку они обеспечивают более сильные перекрестные взаимодействия.

В результате вычислений также получено, что внедрение небольшой группы клеток рыхлого клеточного агрегата в окружающий матрикс является структурно неустойчивым. Некоторые изменения состава рыхлого агрегата, при которых величина начального уплотнения сохраняется, приводят к отсутствию внедрения группы клеток в окружающий матрикс. Так, при начальных условиях ф_с0 = 0,48 , ф_ш0 = 0,035 быстрое начальное уменьшение радиуса агрегата в точности совпадает с уменьшением радиуса в предыдущем случае (ф_с0 = 0,4 , ф-₀ = 0,2), однако эволюция концентраций фаз демонстрирует только формирование полости (как на рис. 2).

Дальнейшее увеличение плотности клеточного агрегата только за счет увеличения содержания в нем матрикса также показывает отсутствие инвазии. В результате вычислений получено, что при начальных условиях ф_с0 = 0,4 , ф-₀ = 0,4 (начальное уплотнение приблизительно 3,5 • R S ) происходит распространение фронта клеточной фазы по матриксу: концентрация клеточной фазы на фронте либо превышает концентрацию в центральной части, либо остается приблизительно такой же (чем ниже концентрация окружающего матрикса, тем выше концентрация клеточной фазы на фронте).

Выполненные расчеты показывают, что устойчивой чертой развития рыхлых агрегатов, в которых начальное содержание клеточной фазы меньше некоторого критического значения, является создание предварительной разметки для последующего развития полой клеточной структуры. Эта особенность сохраняется при различных соотношениях начальных концентраций клеточной фазы и матрикса в рыхлых агрегатах.

Увеличение начальной плотности клеточной фазы выше некоторого критического значения приводит к формированию структуры, отличной от полости, даже если клеточный агрегат можно еще считать рыхлым ( ф_со = 0,635 , ф-₀ = 0,05, величина начального уплотнения приблизительно 3,5 • R_s , как в предыдущем случае). Формирующаяся в этом случае структура характерна для развития плотных клеточных агрегатов.

Б. Эволюция плотных клеточных агрегатов . Рассмотрим эволюцию объемных концентраций твердых фаз в плотном клеточном агрегате, в котором ф_с0 = 0,8 и ф-о = 0,08 при различных значениях ф+₀ . Начальное уменьшение радиуса агрегата составляет приблизительно 0,1 • R . Расчеты показали, что в процессе формирования клеточной структуры происходит образование плотного ядра, окруженного кольцом клеточной фазы, где объемная концентрация клеток существенно отличается от центральной области (рис. 5, а ). Концентрация и распределение клеточной фазы в этом кольце зависит от концентрации окружающего матрикса. При невысокой концентрации матрикса распределение клеточной фазы характеризуется отделением небольшой группы клеток от основной массы (кривые 1 и 2 - рис. 5, а ), тогда как при высокой концентрации матрикса концентрация клеточной фазы в кольце является малой и практически неизменной (кривая 3 - рис. 5, а ). Радиус ядра слабо зависит от концентрации окружающего матрикса, а концентрация клеточной фазы в ядре является почти постоянной. Механические взаимодействия отделяющейся части клеточной фазы с матриксом создают условия для уплотнения матрикса вокруг ядра клеточной фазы (кривые 1 и 2 - рис. 5, б) , которое может быть рассмотрено как образование капсулы.

Эффект отделения группы клеток от основной массы был получен также и в теоретических работах [11; 42], в которых распространение клеток в матриксе описывалось уравнением диффузионного типа для концентрации клеток, учитывающим возможные механизмы активных клеточных взаимодействий. В этих работах было исследовано влияние активных взаимодействий клеток как между собой, так и с матриксом на распространение фронта клеток в недеформируемом матриксе в линейной геометрии. Существенным элементом моделей [11; 42] является ферментативное разрушение матрикса, которое создает неоднородность распределения его плотности.

Постановка задачи в данной работе позволяет получить этот эффект в реальной сферической геометрии с учетом деформируемости матрикса и без привлечения химической активности клеток.

Однако более реалистичное описание отделения группы клеток от основной массы должно быть выполнено в рамках 3 D -постановки без использования предпо-

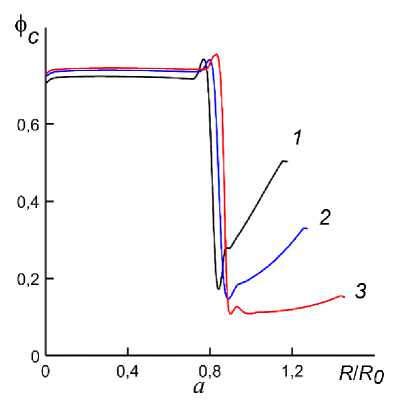
Рис. 5. Распределения концентраций клеточной фазы ( а ) и фазы матрикса ( б) в момент времени t = 4,5 при ф c о = 0,8 , ф _т о = 0,08 и различных ф + ₀ . Кривая 1 - ф т ₀ = 0,4, 2 - ф т ₀ = 0,6 , 3 - ф т ₀ = 0,8

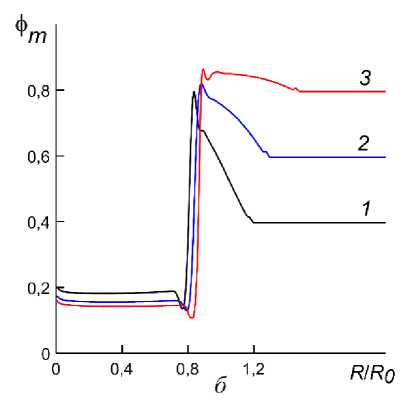
ложения о сферической симметрии. Должно быть исследовано развитие неустойчивости поверхностного слоя клеток, которая проявляется в образовании пальцеобразных клеточных структур.

Распределение клеточной фазы на рис. 5, б, кривая 3 характерно для развития глибластомы (опухоли мозга). Глиобластомы состоят из растущего плотного сфероида, окруженного зоной подвижных клеток низкой плотности, известной как инвазивная зона. Инвазивнная область клеток образует диффузный сферически-сим-метричный рисунок [5; 43; 44].

Во всех случаях инвазивный рост связан с изменением подвижности и адгезии клеток в поверхностном слое опухоли [45]. В рассмотренной задаче не потребовалось вводить пространственную неоднородность свойств клеток. Основными механизмами, контролирующим модель развития, являются активные межклеточные взаимодействия и активные взаимодействия клеток с матриксом, которые в свою очередь определяются составом среды.

Заключение

В работе исследована роль параметров, которые характеризуют систему «клетки - матрикс» только как механическую систему, исключая из рассмотрения эффекты, связанные с делением клеток и выработкой протеолитических ферментов.

Решена задача о развитии структур в клеточном агрегате сферической формы, который окружен вязким внеклеточным матриксом. Математическое моделирование выполнено в предположении сферической симметрии. Разработанная нами ранее континуальная многофазная модель биологической среды, образованной двумя активно взаимодействующими твердыми фазами и жидкостью [21], адаптирована для данного случая, когда одна из твердых фаз образована клетками, а другая -внеклеточным матриксом. Постановка задачи учитывает перемещение границы клеточного агрегата. Ее перемещение определяется условиями, которые учитывают перераспределение нагрузки между клеточной фазой и фазой матрикса по разные стороны от границы агрегата.

Исследована эволюция объемных концентраций клеточной фазы и матрикса в клеточных агрегатах, различающихся начальным составом и активными взаимодействиями клеток как между собой, так и с матриксом.

Численные расчеты показали, что в случае доминирования межклеточных активных механических взаимодействий над перекрестными между клетками и матриксом происходит только уплотнение как рыхлых, так и плотных агрегатов - отсутствие распространения клеток в окружающие ткани или неинвазивное развитие.

Доминирование перекрестных активных взаимодействий над межклеточными приводит к зависимости модели развития клеточных структур от начальной объемной концентрации клеточной фазы. В рыхлых клеточных агрегатах происходит вытеснение клеточной фазы в радиальном направлении в сторону внешней границы агрегата и формирование распределения концентрации клеточной фазы, которое можно рассматривать как начальную стадию формирования полости, окруженной слоем клеточной фазы. В плотных агрегатах происходит формирование плотного ядра и отрыв части клеточной фазы от основной массы - внедрение в окружающие ткани или инвазивное развитие. При этом формируется капсула из внеклеточного матрикса, окружающая агрегат. Более корректное описание развития плотных агрегатов должно быть выполнено в рамках 3 D -постановки без использования предположения о сферической симметрии. Должно быть исследовано развитие неустойчивости поверхностного слоя клеток, которая проявляется в образовании пальцеобразных клеточных структур. Исследование длительной эволюции системы не проводится, поскольку оно имеет смысл только с учетом механизмов, связанных с делением клеток и ферментативным разрушением матрикса.

Полученные результаты имеют значение для понимания роли различных механизмов в процессах образования и развития многоклеточных биологических структур.