Математическое моделирование кариозных процессов, протекающих в зубной эмали, и процесса лечения начального кариеса по технологии ICON

Кариес – это заболевание твердых тканей зуба, которое сопровождается тяжелыми клиническими проявлениями (боль, повышенная чувствительность, эстетический дефект) и может привести к утрате структурно-функциональной целостности всей зубочелюстной системы человека [18]. Известно, что в настоящее время кариозные поражения зубов представляют серьезную проблему для трудоспособной части населения Российской Федерации: почти 90% оказались подвержены данному заболеванию [4, 6, 8, 13, 15, 18, 24, 30]. Решение проблемы снижения распространенности заболевания сводится к наиболее раннему выявлению признаков заболевания, разработке и проведению превентивных мероприятий и поиску максимально эффективного, атравматичного способа лечения, что, несомненно, является актуальной задачей современной стоматологии.

Развитие медицины, в том числе стоматологии, в настоящее время характеризуется ее тесным взаимодействием со смежными дисциплинами – биомеханикой, физикой, химией, математикой, физической химией и др. Это обусловлено необходимостью более адекватных и детальных знаний о строении и функциях органов человека как в норме, так и при заболеваниях, с тем, чтобы иметь возможность проводить наиболее целесообразными путями различного рода медицинские вмешательства [25]. Современный уровень развития основных естественных наук, который позволил проводить систематические фундаментальные исследования, имеющие целью выявить и понять основные закономерности (физикохимические, механические, кибернетические) устройства, функционирования и развития живых организмов, способствовал возникновению такого междисциплинарного сотрудничества, как биомеханика.

Теоретические методы биомеханики основаны на достижениях современной механики, изучающей собственно механическое движение во взаимосвязи с физикохимическими и электромагнитными явлениями и с использованием соответствующего математического аппарата и вычислительной техники. Сейчас развитие получает разработка различных моделей биологических структур и процессов – электрических, электронных, математических и т.п. Примером теоретических работ, связанных с созданием математических моделей, могут послужить статьи [7, 19, 29], рассматривающие кариес зубов как медико-социальное явление, исследования [2, 5, 12, 14 ,22, 33], посвященные изучению зуба (а также зубочелюстной системы) как физического объекта. Кроме того, в настоящее время, в связи с появлением доступной высокопроизводительной вычислительной техники, активно используются программные комплексы, основанные на применении конечно-элементных моделей. Работа [9] является примером часто встречающихся исследований, посвященных определению напряженно-деформированного состояния интересующего объекта с целью дальнейшего изучения его поведения в условиях каких-либо воздействий либо с целью оптимизации некоторой предварительной обработки.

Экспериментальная биомеханика сочетает методы механики с методами, развитыми в биологии и медицине. Часто такие специфические методы в стоматологии, как метод исследования зубного ликвора, тест резистентности эмали, оценка проницаемости эмали, метод химической биопсии, CRT -тест, дополняются исследованиями устойчивости эмали к истиранию путем определения микрошероховатости после воздействия абразивными агентами, исследованиями эмали на микротвердость с применением методов индентирования, электронной и атомносиловой микроскопии [3, 10, 16, 20, 21, 26, 35, 44].

Применение системного подхода к решению проблемы лечения кариеса дало толчок развитию нового способа лечения, позволяющего обойтись без оперативного вмешательства, подразумевающего механические повреждения зуба. Причина 94 ISSN 1812-5123. Российский журнал биомеханики. 2013. Т. 17, № 2 (60): 93–106

зарождения кариеса заключается в нарушении баланса между окислительными и восстановительными процессами, протекающими в системе ротовая полость – зуб – организм [23]. Основной фактор возникновения очага кариозного поражения и возможность его дальнейшего развития устраняется нанесением на поврежденный участок поверхности зуба специального фотополимера, способного проникать вглубь эмали и отвердевать под действием света. Результатом этой процедуры является возникновение между эмалью зуба и агрессивной средой полости рта надежной преграды, дающей организму возможность восстановить кислотно-щелочной баланс твердых тканей зуба.

Существует достаточно много работ, посвященных изучению инфильтрации композитных составов в эмаль, подверженную кариозному повреждению [17, 34, 37–40]. Ввиду очевидных сложностей многие исследования проводятся in vitro , т.е. зуб рассматривается в извлеченном из организма состоянии. Однако зуб по своей структуре весьма сложен, и, что очень важно, при его изучении, как и любой биологической подсистемы, нельзя ограничиться его обособленным состоянием. Лишь только в течение первых нескольких минут исследование умирающего после удаления зуба может дать незначительный объем информации о затухающих, протекающих в нем раньше, живых процессах. Воссоздание условий, имитирующих естественное окружение зуба в его нормальном состоянии, – трудновыполнимая, а потому неэффективная работа.

С точки зрения авторов, очевидна необходимость разработки математической модели, описывающей состояние зубной эмали как составляющей системы ротовая полость – зуб – организм в процессе возникновения и развития кариеса. В дальнейшем, будучи дополненной и усложненной, модель станет основой для исследования эффективности современной технологии лечения, поиска способов ее оптимизации, а также определения возможных ограничений на применение данного метода лечения.

Основные положения

Коронка зуба состоит из трех частей: внутренняя – пульпа, средняя – дентин и наружная твердая оболочка – эмаль. Ее толщина – от 0,1 мм у основания коронки до 2 мм в области жевательной зоны.

Эмаль образована эмалевыми призмами (рис. 1), которые радиально поднимаются от более глубокого слоя – дентина. Благодаря своей структуре эмаль зуба функционирует как «молекулярное сито», а эмалевая жидкость служит переносчиком молекул и ионов.

Рис. 1. Выход эмалевых призм на поверхность зуба

Рис. 2. Проникновение кислоты зубной бляшки по каналам в эмаль и разрушение данной структуры зуба

Кислоты, появляющиеся во рту во время приема пищи, проникают в каналы между призмами, вызывают деминерализацию и в конечном итоге могут привести к разрушению зубной ткани (рис. 2). В качестве ответной реакции организма активизируется защитная система реминерализации пульпы, которая снижает кислотность жидкости, находящейся в эмали и, таким образом, уменьшает вредное воздействие кислот, идущих с поверхности зуба внутрь [23].

Концептуальная модель зубной эмали

Эмаль зуба представлена как сплошная пластина толщиной L , имеющая двухслойную структуру, которая равномерно по площади пронизана каналами. С одной стороны эмаль взаимодействует с внешней средой полости рта, а внутренняя часть зуба (дентин и пульпа) представлена абстрактной областью, в которой может активизироваться защитная система реминерализации (рис. 3).

Каналам заданы среднестатистические размеры [4, 6, 8, 13, 15, 18, 24, 30] и перпендикулярное к поверхности эмали направление. Принимается допущение об отсутствии сообщения каналов друг с другом, что позволяет рассматривать процессы в одном обособленном от остальных канале.

Модель состоит из трех компонентов: канал, заполненный нейтральной жидкостью, и диффундирующие внутрь него кислота и жидкость защитной системы реминерализации (см. ниже). Канал является осесимметричным и описывается своим радиусом в каждой точке x по всей своей длине [0; L ] для любого момента времени t ≥ 0 функцией R = R ( t , x ). Наличие проникших в канал жидкостей определяется значением функции их объёмных долей φ = φ ( t , x ) также в каждой точке канала x и в любой момент времени t . Функция объемной доли кислоты обозначена как φ 1 , а объемной доли жидкости защитной системы реминерализации как φ 2 .

Взаимодействие компонентов модели происходит без производства продуктов взаимодействия. Кислота и жидкость защитной системы реминерализации вступают в реакцию, понижая значение своих объемных долей. Стенки канала (только его боковая поверхность) растворяются под действием кислоты, увеличивая его радиус и, опять же, понижая значение объемной доли кислоты. Изначально канал имеет форму цилиндра. Проникновение жидкостей в канал происходит с его открытых торцов и описывается граничными условиями.

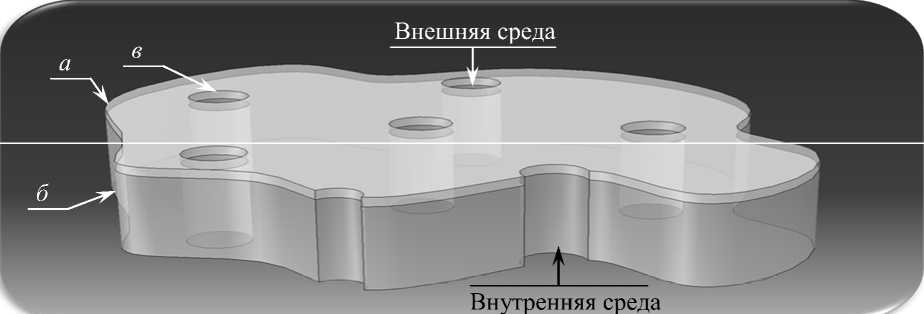
Рис. 3. Схематичное представление структуры эмали: а – слой эмали с повышенной резистентностью к кислоте; б – с пониженной; в – каналы, в которых находится межпризменное вещество и эмалевая жидкость

Схематичное представление этапов развития кариеса

	Эмаль (поперечный разрез)					Стадии процесса
	Внешняя среда Нейтральный рн		1     2 ->      Внутренняя Среда 1     2 __Нейтральный 3        pH 1     2			Здоровое состояние (1)    – слой эмали с повышенной резистентностью к кислоте (за счет контакта со слюной и повышенного содержания фторапатитов); (2)    – слой эмали с пониженной резистентностью к кислоте; (3)    – каналы, в которых находится межпризменное вещество и эмалевая жидкость
	4 ИсТОЧ! кислс сред.	^^\	12   м 3 Ж 1 2 ■ 1   2 X	5 щитная 1стема линера-13ЭЦИИ		Состояние начального кариеса зубная бляшка (4) закрывает поверхность от слюны и выделяет кислоту, которая попадает в каналы (3); кислота начинает разъедать стенки каналов (3); активизируется защитная система (5); (3) – противостояние (4) и (5)
	4 Источник кислой среды		1 2 1 2 ■ 1     2	5 щитная истема чинера-изации		Возможное развитие зубная бляшка (4) разрастается; (3) – поток кислоты увеличивается; защитная система реминерализации (5) не справляется со своей функцией; происходит увеличение радиуса каналов: в слое (1) медленное, в (2) – быстрое

Моделирование процесса деминерализации эмали зубов

Для математической постановки модели выделим объем канала с малой длиной Δ x и площадью поперечного сечения S = π R ².

Учитывая, что длина канала как минимум на два порядка больше его радиуса, можно ограничиться одномерной постановкой. Принимается гипотеза о том, что процессы, связанные с воздействием кислоты на стенку канала, проходят в пренебрежимо тонком слое Δ h (рис. 4).

Из работ [11, 28] следует, что изменение концентрации кислоты (ρ 1 ) в выделенном элементарном объеме канала (см. рис. 4), в котором присутствует ее объемный сток ( J 12 V ρ 1 ρ 2 ), вызванный воздействием жидкости защитной системы реминерализации (ρ 2 ), описывается балансовым соотношением

/IP ¹ dV ⁼J d ^f D ^^L ^ dV - J 2 V ^№-                °)

V d t      Vdx V   dx )

где ρ 1 и ρ 2 – концентрации кислоты и жидкости защитной системы реминерализации соответственно; µ 1 – химический потенциал кислоты; D 1 – коэффициент диффузии кислоты; J 12 – параметр взаимодействия кислоты и жидкости защитной системы реминерализации; V = S Δ x = π r² Δ x.

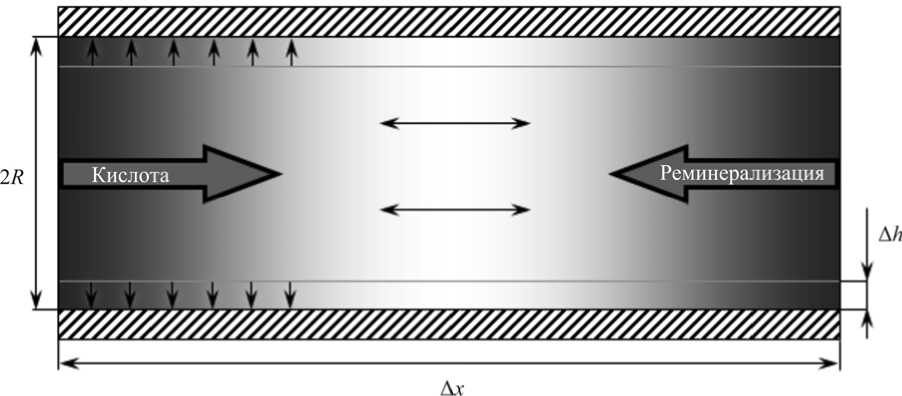
Рис. 4. Контрольный объем в канале

Предполагая, что в малом объеме изменение концентрации ∂ρ 1 /∂ t пространственно однородно, запишем

Г   dv «^ ^ ^ x .

V 5 t         9 t

Далее рассмотрим правую часть уравнения (1) как разницу потоков в точках x и x+ Δ x и сток массы на боковой поверхности канала S бок в слое Δ h :

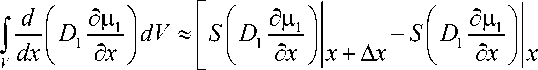
- kSSбокР1 = kSSбокР1,

= kx—I SD1 ^1

9x V    9x

-

где k S – параметр расхода кислоты при растворении стенок канала; S бок = 2π r Δ x . Таким образом, подставляя выражения (2) и (3) в (1), получим

^ r 2 d t

— | r ² D — - 2 k_sr p, - J r ²p,p,.

1 S 11212

9x V

Действуя аналогично, получим уравнение для изменения концентрации жидкости защитной системы реминерализации дР2 2 _ d f 2 d^2 )

- r -I r D2 - I J21 r pip2 .

91 dx V

Радиус канала изменяется только под действием поступающей кислоты. Будем предполагать, что скорость изменения радиуса канала пропорциональна концентрации кислоты и площади его внутренней поверхности, тогда получим уравнение

— = 2ПrkR (x)P dt где kR(x) – параметр, отражающий скорость «разъедания» стенок канала в зависимости от их химических свойств. Для замыкания системы уравнений (4)–(6) запишем химический потенциал в виде (подробнее см. [11, 28])

ц = c r ^е ( in ( ф ) + 1 -Ф+х ( 1 ^-ф ) ² ) ,

где C_r - газовая постоянная; 6 - температура; х — параметр взаимодействия Флори -Хиггинса (х < 0,5); ф - объемная доля, ф = р /р⁰; р⁰ - плотность чистой компоненты. Тогда

8ц ₌ гц8ф_{= C r} е F ( _ф ) 5ф , F ^ = 0 -ф^{)( 1} - ² Х ^ф) . д x Эф д x          ' Xx                ф

Проводя обезразмеривание, выбираем в качестве характерного радиуса величину r ₀ (начальный радиус канала); характерного значения плотности р i - плотность чистой i -й компоненты р ⁰ ; характерного значения переменной x - величину L (длина канала); характерного времени - величину A t = ( 2 п /\'S p 0 ) , где K - характерное значение функции k_R ( x ). Тогда система уравнений (4)-(6) примет вид

S1R2 ^ = Af R2 F (Ф1)^1 - YR Ф1 - а,2 R 2ф,ф2,(9)

О t   Оx Vд

£2 R1^ = Af r2f (ф1) Al 1-а ^ R ^ф(10)

д t    о x Vд

= Kr(x)Rф1, x g (0,1), t g (0,T),(11)

дt где R = R(t, x), ф1 = ф1(t, x), ф2 = ф2(t, x) - функции зависимости радиуса канала, объемной доли кислоты и жидкости защитной системы реминерализации от времени t и глубины канала x.

т 2^0

L ^р

£1 = ¹ , а_п

¹ d.c_r еА t     ¹¹

1 R

1^0^0

= J 11 ^L P 1 ^р 1

DC_r A t ,

1 R

т 1_/-0                   т г2_А0_0                ъг 0 т 1

L Рэ            J L Pi Рэ       2 П. K q L

£.-----, а₂₁ = ¹¹        . y =----- S— . (11)

• ¹    d,c_r еА t    ¹¹ d,c_r a t        dc_r е

• 2    R                       1 R                   1 R

  K r ( x ) =

  
  

  5 ,

  1,

  
  

  x G [0, x 0 ], x G ( x 0 ,1],

  
  

  5< 1,

  
  
  
  

где D i - коэффициент диффузии; C_r - газовая постоянная; 6 - температура; J i ₂ ( J 21 ) - параметры расхода кислоты (жидкости защитной системы реминерализации) при взаимодействии друг с другом; K_R ( x ) - параметр скорости разъедания стенок канала; R , ф 1 , ф₂, t , x - безразмерные величины.

Здесь и в дальнейшем обозначения для безразмерных переменных t и x остаются прежними. Функция (13) учитывает двухслойную структуру эмали, внешняя часть которой представляет собой тонкий слой с повышенной резистентностью к кислоте.

Граничные условия, отражающие процесс поступления кислоты (на левой границе, см. рис. 4) и жидкости защитной системы реминерализации (на правой границе) в канал имеют вид

, _             дф,(t,1) _    Эф,(t,0) Л ф1( t,0) = ф1( t X —т---= 0, — ----= 0 ф1( t ,1) = ф1( t).          (14)

д x            д x

Начальные условия соответствуют каналу, не подвергнутому воздействию кислоты, с минимальным присутствием кислоты и жидкости защитной системы реминерализации, обеспечивающим невырожденность функции F (ф) (8):

ф 1 (0, x ) = £ , ф ₂ (0, x ) = £ ,   ( £ * 0),    R (0, x ) = 1.

Будем исследовать процесс при поступлении в канал жидкостей с постоянной концентрацией: ф * ( t ) = ф ( ⁰⁾ = const, ф 2 ( t ) = ф 2 ⁰⁾ = const, что может соответствовать наличию кариозной бляшки на поверхности зуба.

Очевидно, что характерное время диффузии и установления химического равновесия системы кислота – жидкость защитной системы реминерализации на несколько порядков меньше характерного времени деминерализации и, следовательно, ε 1 , ε 2 << 1. В этом случае задачу можно решать в квазистационарной постановке:

d-1 R2 (t, x)F(ф1) dф1(x) | - уR(t, x)ф1 (x) - a12R2(t, x)ф1 (x)ф2 (x) = 0,(16)

dx V d f R2 (t, x)F(ф2 ) dф2 (x) ) -a21R2(t, x)ф1 (x)ф2 (x) = 0 , dx V

R (t, x) = exp (f (x )ф1( x) t),(18)

ф1(0) = ф*, ф ‘2(0) = 0, ф '1(1) = 0, ф2(1) = ф2.(19)

Краевая задача (16)–(19) решалась численно методом установления с помощью консервативной неявной разностной схемы [27].

Поскольку реальные значения констант-параметров, входящих в построенную модель, неизвестны, обсуждаемые ниже результаты расчетов носят скорее качественный характер и выявляют особенности моделируемого процесса. На рис. 5 представлено распределение радиуса каналов в моменты времени t = 1, 2, 3 для следующего набора параметров:

a ₁₂ =a ₂₁ = 1000, у = 1, х = 0,3, x ₀ = 0,1, 5 = 0,2, ф * = ф 2 = 0,25.      (20)

В этом случае поверхностный слой в 5 раз более устойчив к воздействию кислоты, чем остальная часть эмали. Из рис. 6 видно, как канал приобретает бутылкообразную форму и возникает возможность появления крупных пор за счет слияния каналов в самых широких местах. Причем если считать начальную просветную площадь пористой эмали за 25%, то при t = 1, 2, 3 ее максимум в точке x = 0,1 увеличивается до 34; 45 и 59% соответственно.

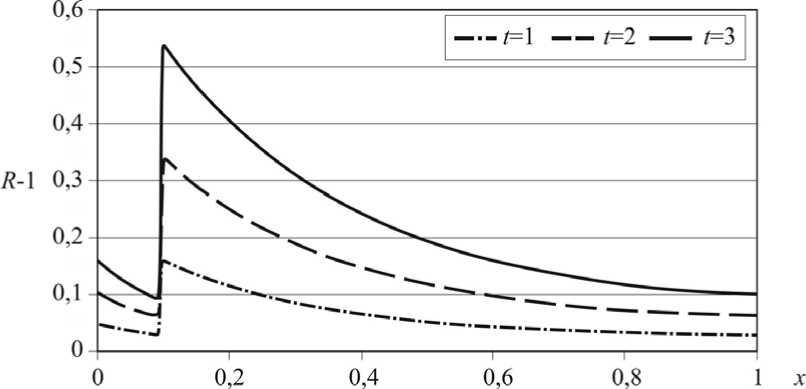
Рис. 5. Распределение радиуса канала вдоль его длины в моменты времени t = 1, 2, 3

Таким образом, деминерализация зуба происходит неравномерно вдоль канала эмали, что связано с неравномерностью концентрации кислоты и свойств зубной ткани.

Полученные результаты хорошо согласуются с клинической картиной кариеса, когда подповерхностный, менее резистентный к кислоте слой эмали разрушается быстрее поверхностного слоя (рис. 6) с образованием малозаметного белого пятна. Более выраженная патология в виде коричневого пятна проявляется только в развитой фазе заболевания, что препятствует его ранней диагностике и лечению.

Представляет интерес анализ кислотно-щелочной среды по мере изменения формы канала. На рис. 7 представлены распределения объемных долей кислоты и жидкости защитной системы реминерализации в моменты времени t = 1 и t = 3 . Откуда видно, что анализируемые распределения слабо зависят от формы канала (момента времени).

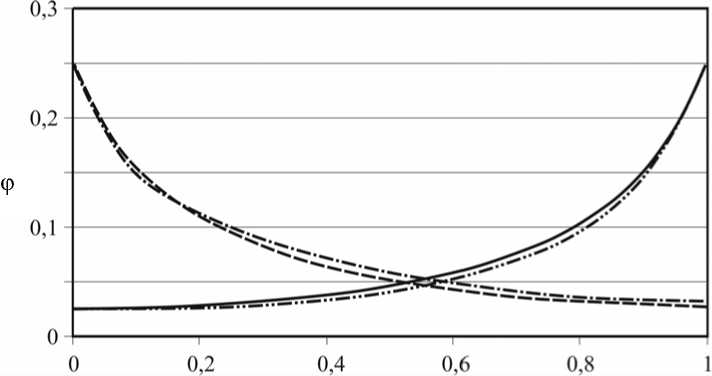
Объемные доли:

кислоты t = 1

кислоты t = 3

ЗСР t = 1

ЗСР t = 3

Рис. 7. Распределение объемных долей кислоты и жидкости защитной системы реминерализации (ЗСР) в разные моменты времени

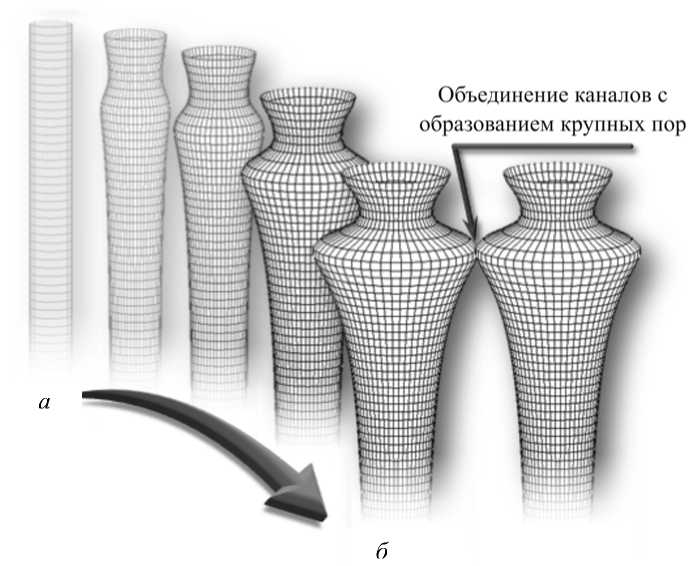
Рис. 6. Процесс деминерализации эмалевых каналов: а – здоровое состояние эмали, б – начальный кариес

Таблица 1

Соотношение значений R -1 в точках x = 1 и x = 0,1

Вариант	t = 1	t = 2	t = 3
1	0,030/0,163	0,065/0,345	0,105/0,544
2	0,089/0,210	0,190/0,446	0,302/0,705
3	0,169/0,247	0,372/0,541	0,608/0,880

Таблица 2

Значение просветной площади (%)

Вариант	t = 0	t = 1	t = 2	t = 3
1	25,0	33,8	45,2	59,3
2	25,0	36,6	52,3	72,3
3	25,0	38,9	59,3	90,3

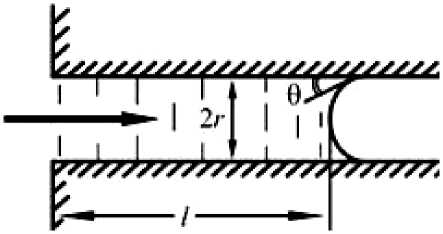
Рис. 8. Перемещение жидкости на длину l в капилляре радиуса r : θ – краевой угол

Для выяснения влияния интенсивности реакции нейтрализации на формирование канала были просчитаны три варианта, в которых использовались параметры (20) за исключением значений α 12 и α 21 :

• 1)    α 12 = α 21 = 1000;

• 2)    α 12 = α 21 = 100;

• 3)    α 12 = α 21 = 10.

Во всех трех случаях решение имело вид аналогичный рис. 5, менялось только значение радиуса в точке x = x 0 = 0,1 (максимум) и x = 1 (минимум). Результаты расчетов представлены в табл. 1, откуда видно, что исследуемые величины зависят от времени почти линейно.

Более наглядное представление о характере процесса дает табл. 2, в которой приводятся значения просветной площади (в процентах) при x = x 0 = 0,1 для анализируемых вариантов параметров в три момента времени. Откуда видно, что при t = 1 различие результатов для разных вариантов относительно невелико и их можно относить к ранней стадии кариеса, доступной для лечения с помощью технологии ICON . С увеличением времени это различие становится все более существенным и кариес переходит в более развитые стадии.

Моделирование технологии ICON

Технологию ICON можно условно разделить на четыре этапа:

• 1)    удаление поверхностного слоя с помощью химического воздействия;

• 2)    нанесение на поверхность эмали композитного материала;

• 3)    проникновение композитного материала в каналы эмали;

• 4)    затвердевание композитного материала под воздействием света.

102                     ISSN 1812-5123. Российский журнал биомеханики. 2013. Т. 17, № 2 (60): 93–106

Рассмотрим модель процесса проникновения композитного материала в каналы эмали. Поскольку размеры каналов от 2 до 5 мкм, основным механизмом такого проникновения являются капиллярные силы. Схематично этот процесс представлен на рис. 8.

Скорость v перемещения мениска в очень тонком вертикальном капилляре, когда влияние силы тяжести мало, определяется уравнением Пуазёйля:

r ² A p    ,     „ cos 0

v = -"-- 7, ^A P = ^{- 2} ^ i2----

8n I                   r где l – длина участка впитавшейся жидкости; η – ее вязкость; Δp – перепад давления на участке l; σ12 – поверхностное межфазное натяжение [1]. В рассматриваемой задаче имеем r = r(l), где l – координата вдоль стенки канала, тогда, если краевой угол θ не зависит от скорости v, можно рассчитать глубину проникновения впитавшейся жидкости из уравнения dl(t)     z r("(l)        о ^n cos 0,

= v(t,l) = e^, где в = ^2-----.(22)

dt               l4

Пусть необходимо заполнить канал длиной L = l(T), тогда из уравнения (22) следует ldl

R ( l )

= P r^dt и T = — \ldl- , 0             в r o ^J 0 R (l )

где T – время заполнения канала. В простейшем случае R ( l ) ≡ 1 получаем

T = -L-

0 2 P r o'

С учетом криволинейности стенок капилляра (рассчитанной во второй части работы, см. рис. 5) и перехода в декартову систему координат окончательно получаем

T = ₂ p Vl + ( R '( x ) ) 2 T o    ^J o      R ( x )

dx .

В табл. 3 представлены результаты расчетов, полученные для трех вариантов формы канала (в зависимости от параметров α 12 и α 21 ), где t – время окончания кариозного процесса. С учетом того, что начальный радиус каналов r 0 = 3,5±1,5 мкм, положив в формуле (24) его среднее значение, получим T 0 = T 0 ,cp (1±0,43). Тогда с помощью данных табл. 3 можно рассчитать минимальное и максимальное время процесса заполнения канала для разных вариантов исходных параметров и разного времени t .

Таблица 3

Значение T / T ₀

Вариант	t = 1	t = 2	t = 3
1	0,952	0,926	0,910
2	0,899	0,827	0,771
3	0,839	0,716	0,617

Выводы

На основе имеющихся в настоящее время данных о физиологии человеческих зубов была разработана физическая модель, описывающая эмаль как сплошную двуслойную среду, пронизанную каналами, и основные протекающие в ней процессы (диффузия жидкостей из внешней среды и внутренних слоев зуба; химическое взаимодействие жидкостей и их влияние на эмаль), которая стала основой для математического описания кариозного заболевания.

Используя фактор различия характерных временных масштабов для процессов химической кинетики и изменения формы канала при разрушении ткани зуба, разработанную математическую модель сформулировали в квазистационарном приближении. На базе полученной математической модели было проведено исследование процессов, происходящих в микроканалах зубной эмали, в результате которого была получена информация об эволюции формы каналов эмали в течение развития кариозного повреждения, что позволяет судить об изменении пористости эмали по глубине и для любого конкретного момента времени. Анализ результатов показал, что созданные модели правдоподобно отображают особенность исследуемого явления, которая заключается в неравномерности деминерализации эмали.

Данные об изменении структуры эмали, полученные с помощью расчетов на основе модели нелинейной диффузии химически реагирующей смеси кислота – жидкость защитной системы реминерализации в квазистационарном приближении, были учтены при дальнейшем исследовании процесса проникновения в эмаль композита, применяемого в технологии лечения кариеса, основным механизмом которого являются капиллярные силы. Изменение структуры эмали на микроуровне заключается в том, что ее микроканалы, будучи изначально цилиндрическими, приобретают бутылкообразную форму, что сказывается на значении капиллярных сил и, следовательно, на эффективности инфильтрации композита и лечения в целом. Была получена формула, позволяющая рассчитать минимальное и максимальное время процесса заполнения пор эмали в зависимости от степени поражения эмали кариесом и для различных вариантов исходных параметров.

Благодарности

Работа выполнена при финансовой поддержке гранта РФФИ № 11-01-96028-р_урал_а.

Пермского университета. Математика. Механика. Информатика. – 2012. – № 2. – С. 20–25.

ISSN 1812-5123. Российский журнал биомеханики. 2013. Т. 17, № 2 (60): 93–106                      105