Математическое моделирование кинетики многократного приёма этанола



Экспертная оценка кинетики этанола является одной из важных проблем современной судебной медицины, актуальность которой определяется нормативно-правовыми особенностями многих стран [1–3]. В первую очередь, указанные особенности связаны с наличием допустимых пределов концентрации этанола в организме при вождении автомобиля. Кроме того, законодательствами ряда государств определённый уровень содержания алкоголя в организме в момент совершения преступления рассматривается как обстоятельство, смягчающее наказание.

Изложенное вызывает необходимость установления экспертным путем количественного содержания алкоголя в организме обвиняемого в юридически актуальный момент времени. В настоящее время из числа пригодных для экспертной практики кинетических моделей наиболее физиологически обоснованной является модель элиминации нулевого порядка с абсорбцией и безвозвратным дефицитом абсорбции первого порядка:

C_t = —(1- e"k a t ifl-—Vp t,        (1)

t rM            k

a где Ct – концентрация этанола в крови в момент времени t, г/кг; m – масса принятого этанола, г; r – коэффициент распределения этанола; М – масса тела, кг; kd – константа извлечения, ч-1; ka – константа абсорбции, ч-1; β – почасовая скорость элиминации этанола, г/(кг·ч); t – время после приёма алкоголя, ч [4].

Вместе с тем, модель (1) предназначена для описания однократного перорального приёма алкоголя. Однако на практике приём алкоголя зачастую бывает не однократным, а представляет собой серию из нескольких эпизодов, разделённых промежутками времени различной продолжительности. Объёмы и крепость принятых алкогольных напитков также могут различаться. Это вызывает необходимость разработки кинетической модели многократного приёма этанола. В настоящее время в судебно-медицинской практике используются два основных метода решения этой проблемы.

Первый метод заключается в приближении многократного приёма алкоголя кинетикой его однократного приёма путем суммирования принятых доз. Последующие расчёты производятся с тем лишь отличием, что в качестве показателя количества принятого этанола учитывается сумма его масс по каждому эпизоду приёма [5]. Данный метод обычно применяется в качестве приближения серии из нескольких приёмов спиртных напитков, разделённых друг от друга небольшими промежутками времени [5]. В рамках кинетической модели (1) изложенный подход для серии из n приёмов этанола описывается выражением

C = m^ m 2..... m „ ( e -_v<1 - k I t .

t rM                 k

a

Второй метод заключается в расчёте уровней этанолемии в актуальный момент времени отдельно для каждого приёма алкоголя с последующим суммированием полученных концентраций [6]. Применительно к кинетической модели (1) названный метод описывается уравнениями

C = m L (1 - e - ^k a t i jf 1 - kd )-p t ,

• ¹    rM^v ]     k_a J i

n

C total = S C i .

i =1

Метод суммирования концентраций, напротив, полностью соответствует реальной кинетике только при условии повторного приёма этанола спустя длительный промежуток времени, в течение которого элиминация принятой ранее дозы алкоголя успевает завершиться его полным выведением из организма. При укорочении этого временного промежутка оценки этанолемии соответствуют физиологическим только в фазу абсорбции этанола.

В этой связи для многократного приёма алкоголя необходимо построение адекватной матема- тической модели, учитывающей кинетические особенности данного феномена. В частности, необходимым является учёт следующих параметров:

• -    количеств этанола, принятых в рамках каждого эпизода из серии приёмов;

• -    промежутков времени между каждым предыдущим и последующим приёмами алкоголя;

• -    фракций этанола предыдущих приёмов, удаляемых в результате его пресистемного метаболизма;

• -    количеств этанола предшествующих приёмов, попавших в системный кровоток ко времени следующих эпизодов приёма;

• -    уровней этанолемии на момент каждого последующего приёма алкоголя;

• -    количеств этанола предыдущих приёмов, удалённых из организма в результате его метаболизма и выведения в неизмененном виде ко времени каждого последующего приёма алкоголя;

• -    возможных изменений значений констант абсорбции и извлечения после каждого последующего приёма алкоголя.

Располагая информацией об указанных параметрах возможно описание кинетики многократного приёма этанола, которое будет максимально соответствовать физиологической. Построить такую математическую модель можно на основе кинетического уравнения (1) элиминации нулевого порядка с абсорбцией и её безвозвратным дефицитом первого порядка. При этом процедура математического моделирования, помимо построения кинетической модели, должна также включать в себя разработку реализующего её вычислительного алгоритма и компьютерной программы.

Изложенное определило цель исследования – построение на базе кинетического уравнения элиминации этанола нулевого порядка с абсорбцией и безвозвратным дефицитом абсорбции первого порядка математической модели кинетики многократного приёма этанола, а также её реализация в формате компьютерной программы.

Материал и методы исследования

Методологический дизайн исследования представляет собой аналитическое математическое моделирование кинетики многократного перорального приёма этанола на основе модели элиминации нулевого порядка с абсорбцией и её дефицитом первого порядка.

Код программы для электронно-вычислительной машины составляли на языке программирования C# с использованием бесплатно распространяемой версии приложения Microsoft Visual Studio .

Результаты исследования

Рассмотрим вначале наиболее короткую серию из двух приёмов алкоголя. До момента повторного употребления алкоголя его кинетика соответствует модели (1) однократного приёма, в рамках которой количество удаленного в результате пресистемного метаболизма этанола на момент его повторного приёма определяется уравнением

E i = m i k d¹ ( 1 - e -^k a ¹ t ¹ ) , (2) k a 1

где Е 1 – фракция этанола первого приёма, удаляемая в результате его пресистемного метаболизма до момента повторного приёма, г; m 1 – количество этанола первого приёма, г; t 1 – промежуток времени между первым и повторным приёмами алкоголя, ч; k d1 , k а1 – константы извлечения и абсорбции для промежутка времени t 1 , ч^-1.

Тогда количество этанола, попавшего в системный кровоток за время t 1 , равно

A = m 1 ( l- e ^{- k} a ¹ t ¹ ) - E 1 , (3) где А 1 – количество этанола первого приёма, попавшего в системный кровоток ко времени повторного приёма алкоголя, г.

Количество этанола, подлежащего элиминации ко времени повторного приёма алкоголя, определяется произведением b1 = в • r • M • t1, где b1 – количество абсорбированного этанола первого приёма, которое при условии его наличия может быть удалено из организма при заданной скорости элиминации ко времени повторного приёма алкоголя, г.

Очевидно, что реальное количество этанола первого приёма, подвергшегося элиминации в течение промежутка времени t 1 , определяется правилом:

fB1 = b1, если A, > b1 (4) [B1 = A1, если A, < b1’ где В1 – количество этанола, подвергшегося элиминации в промежуток времени t1, г.

Отсюда содержание этанола в крови ко времени повторного приёма можно вычислить через разность количеств абсорбированного и элиминированного алкоголя:

с, = AlB ,

• 1    rM

где С 1 – концентрация этанола в крови ко времени повторного приёма алкоголя, г/кг.

После повторного употребления алкоголя его кинетика отклоняется от модели (1) однократного приёма в связи с наличием в гастроинтестинальном тракте остаточных количеств алкоголя, не подвергшихся абсорбции и пресистемному метаболизму. Вновь принятый алкоголь добавляется к остаточному его объёму, в связи с чем количество этанола, удаляемого путем пресистемного метаболизма после его повторного приёма, следует определить как

, - k =2 t 2 ) ,

^E ₂ = ⁽ m , + m 2 - E 1 - A ,)     ⁽ 1 - e

k a2

где t 2 – время после повторного приёма алкоголя, ч; Е 2 – фракция этанола первого и повторного приёмов, удаляемая за период времени t 2 , г; m 2 – количество этанола повторного приёма, г; k d2 , k а2 – константы извлечения и абсорбции для промежутка времени t 2 , ч^-1.

Аналогичным образом модифицируется и уравнение абсорбции:

A2 = (m, + m2 - A1 - E,)(, - e”ka2t2)- E2, где А2 – количество этанола первого и повторного приёмов, попавшего в системный кровоток после повторного приёма алкоголя к моменту времени t2, г.

Количество этанола, которое может быть элиминировано после повторного приёма алкоголя, определяется произведением b2 =p-r ■ M ■ 12, где b2 – количество этанола, которое при условии его наличия и заданной скорости элиминации может быть удалено из организма в течение промежутка времени t2, г.

Аналогично реальное количество этанола, подвергшегося элиминации в течение промежутка времени t 2 , определяется правилом:

B ₂ = b ₂ , если ( A , + A ) > ( B , + B ₂ )

B2 = A, + A2 - B,, если (A, + A2 )<(B, + B2) ’ где В2 – количество этанола, подвергшегося элиминации в промежуток времени t2, г.

В итоге содержание этанола в крови после серии из двух приёмов алкоголя в рамках кинетики элиминации нулевого порядка с абсорбцией и её безвозвратным дефицитом первого порядка описывается уравнением

^C2 =

A , + A ₂ - B , - B ₂ rM

где С 2 – концентрация этанола в крови в момент времени t 2 , г/кг.

Предложенный метод моделирования кинетики повторного приёма алкоголя, который можно условно назвать методом кинетического суммирования, в наибольшей степени соответствует физиологической фармакокинетике, в т.ч. предусматривая и возможность изменения констант абсорбции и извлечения по мере приёма алкоголя.

Пример 1

Мужчина весом 100 кг принял внутрь сначала 200 мл, а затем, спустя 1 ч после первого приёма, еще 300 мл водки крепостью 40°. Необходимо определить концентрацию этанола в крови субъекта через 5 ч после повторного приёма водки, приняв константы абсорбции и извлечения постоянными и равными 2 ч-1 и 0,3 ч-1 соответственно, а значения фактора редукции и почасовой скорости элиминации этанола – 0,7 и 0,15 г/(кг·ч) соответственно.

По условию задачи имеет место серия из двух приёмов алкоголя, разделённых промежутком времени t 1 длиной 1 ч. Для её решения сначала необходимо рассчитать количество этанола для каждого эпизода его приёма:

• m , = 200 мл ■ 0,4 ■ 0,789 г/мл = 63,, 2 г, m ₂ = 300 мл ■ 0,4 ■ 0,789 г/мл = 94,68 г.

Далее для промежутка t 1 следует вычислить количество этанола, удаляемого в результате его пресистемного метаболизма, попавшего в системный кровоток, а также подвергшегося элиминации:

• E , = 63,12 ■ -023 ■ ( , - e ~²^ ) = 8,187 г,

• A ,    = 63,, 2 ■ ( , - e ^{- 2}■¹ ) - 8, 87 = 46,39, г,

• B ,    = b , = 0,15 ■ 0,7 ■ ,00 ■, = ,0,5 г.

Отсюда концентрация этанола в крови ко времени повторного приёма равна:

_ _ 46,391-10,5

C —               — 0,51

¹       0,7 • 100

г/кг.

Промежуток времени t 2 от повторного приёма водки до актуального момента, на который требуется определить содержание этанола в крови, равен 5 ч. Для данного промежутка аналогичные кинетические параметры имеют следующие значения: E 2 — ( 63,12 + 94,68 - 8,187 - 46,391 ) • 03 • ( 1 - e 25 ) — —15,483 г,

A ₂ — ( 63,12 + 94,68 - 8,187 - 46,391 ) • ( 1 - e 5 ) -

• - 15,483 — 87,735 г,

B 2 — b 2 — 0,15.0,7.100.5 — 52,5 г.

Таким образом, спустя 5 ч после повторного приёма водки этанолемия при заданных значениях ключевых кинетических параметров составит

_ _ 46,391 + 87,735 -10,5 - 52,5

C o —-------------------------------- — 1,02 l/KI.

• ²               0,7.100

В рассматриваемом примере для обоих отрезков времени t 1 и t 2 количество этанола, подвергшегося элиминации, соответствует потенциально возможному для заданной её почасовой скорости, т.е. выполняются равенства

B 1 — b 1 и B ₂ — b ₂ .

Однако данные условия нарушаются, если первая принятая доза этанола будет меньше 45,27, а повторная – меньше 34,85 г этанола.

Пользуясь изложенным вычислительным алгоритмом, можно описать динамику содержания этанола в крови для данных из рассматриваемого примера за весь период нахождения алкоголя в организме (рис. 1). Следует отметить, что в предложенной кинетической модели повторного приёма алкоголя весьма важную роль играет промежуток времени между эпизодами приёма (рис. 2).

Изложенный метод кинетического суммирования можно обобщить на любое количество эпизодов приёма алкоголя, разделённых временными промежутками 1 1 , 1 ₂, _ t n _ 1 , где n - число приёмов. При этом последний промежуток t n представляет собой отрезок времени после последнего приёма алкоголя до актуального момента времени, на который требуется определить количественное содержание этанола в крови.

Вычислительный алгоритм метода кинетического суммирования имеет итерационный характер и состоит из n итераций, число которых равно числу приёмов алкоголя. На каждой итерации для соответствующего временного промежутка вычисляются количества абсорбированного этанола, а также удаляемого путём пресистемного метаболизма.

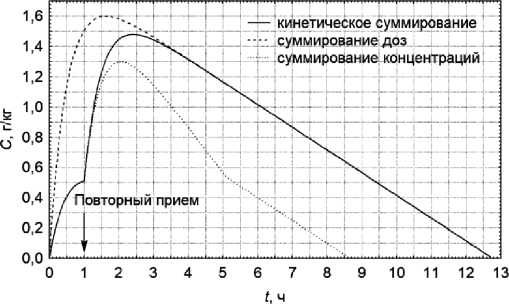
Рисунок 1. Содержание этанола в крови при повторном употреблении 300 мл водки крепостью 40° спустя 1 ч после первичного приёма 200 мл в соответствии с различными кинетическими моделями многократного приёма алкоголя

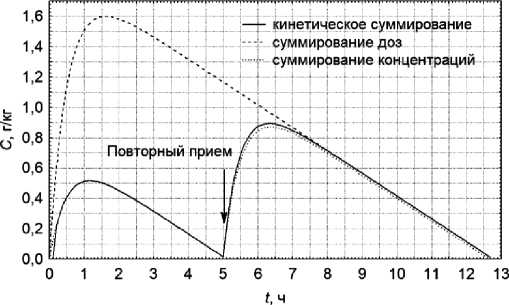
Рисунок 2. Содержание этанола в крови при повторном употреблении 300 мл водки крепостью 40° спустя 5 ч после первичного приёма 200 мл в соответствии с различными кинетическими моделями многократного приёма алкоголя

Figure 1. The ethanol content in the blood during repeated consumption of 300 ml of vodka with a strength of 40 ° 1 hour after the initial intake of 200 ml in accordance with various kinetic models of repeated alcohol intake

Figure 2. The ethanol content in the blood during repeated consumption of 300 ml of vodka with a strength of 40 ° 5 hour after the initial intake of 200 ml in accordance with various kinetic models of repeated alcohol intake

При этом для первого приёма алкоголя указанные кинетические параметры оцениваются по формулам (2)–(4), а для каждого последующего – согласно выражениям k       k—1      k—1

Ek = |zmi— ZEi —ZA|(1 — e"kaktk), (5) i=i         i=i        i=i ak k        k—1

A k = | Z m i — Z E — Z A | ( 1 — e" k ak t k ) — E k , (6)

Vi=1         i=1        i=1

где k = 2..... n - номер итерации.

Также на каждой итерации определяется количество этанола, которое может быть выведено из крови при заданной почасовой скорости элиминации:

b i = в • r • M • t i .

Полученное значение b i затем используется для оценки реального количества этанола, подвергшегося элиминации в течение промежутка времени t i . Для первого приёма алкоголя указанный кинетический параметр вычисляется согласно (4), а для каждого последующего – согласно правилу:

B_k = b_k , если ZZ a ^Z^ B,-

J                           i=1         i=1                                /ух k       k—1             k        k .     (7)

Bk = Z A — ZBi, если Z A < ZBi i=1         i=1                i=1         i=1

Тогда содержание этанола в актуальный момент времени равно

C n

n rM V Z1A

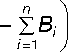
Пример 2

Имеет место серия из 10 приёмов по 100 мл водки, разделённых равными промежутками времени, для мужчины весом 100 кг при тех же параметрах абсорбции, распределения и элиминации. Установить уровень этанолемии после последнего приёма алкоголя при равенстве промежутков между его приёмами 6, 30 и 60 минутам. Отрезок времени после последнего приёма принять равным промежуточным.

Масса этанола для каждого эпизода его приёма составляет mi = 100 мл • 0,4 • 0,789 г/мл = 31,56 г.

Условие задачи подразумевает выполнение 10 итераций для каждого значения промежутков времени между приёмами алкоголя. Для первой итерации вычисления производятся по формулам

(2)–(4), а для остальных – по формулам (5)–(7). Результаты всех итерационных вычислений табулированы (табл. 1). Также приведена геометрия динамики содержания этанола в крови во всех трёх сериях приёма водки (рис. 3).

t, ч

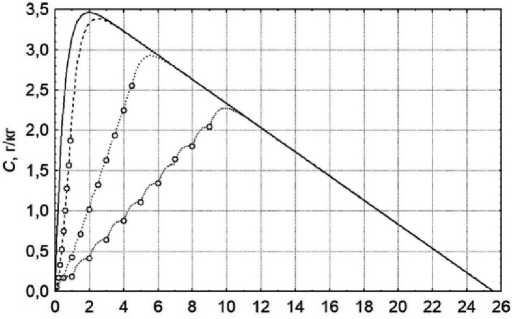
Рисунок 3. Динамика содержания этанола в крови в трёх сериях из 10 приёмов по 100 мл водки, разделённых промежутками времени в 6 (штриховая линия), 30 (крупный пунктир) и 60 (мелкий пунктир) минут. Для сравнения приведена динамика этанолемии при однократном приёме 1000 мл водки (сплошная линия)

Figure 3. The dynamics of the blood ethanol concentration in three series of 10 doses of 100 ml of vodka, separated by time intervals of 6 (dashed line), 30 (large dotted line) and 60 (small dotted line) minutes. For comparison, the dynamics of the blood ethanol concentration with a single intake of 1000 ml of vodka (solid line) is given

Для автоматизации расчётов комплекс изложенных вычислительных процедур был реализован на языке С# в виде приложения «Alcohol Calculator V 3.0» (свидетельство о государственной регистрации программы для ЭВМ № 2022684384). Приложение актуально для серии до 10 эпизодов приёма различных алкогольных напитков, разделённых любыми промежутками времени.

Обсуждение результатов исследования

В рамках проведенного исследования в качестве наиболее адекватного способа математического описания кинетики многократного приёма этанола предложен метод кинетического суммирования, реализованный на основе модели элиминации нулевого порядка с абсорбцией и безвозвратным дефицитом абсорбции первого порядка. До этого в экспертной практике аппроксимация многократного приёма осуществлялась методами суммирования доз и концентраций [5, 6].

Таблица 1. Результаты расчётов для данных из примера 2

Table 1. Calculation results for the data from Example 2

i	1	2	3	4	5	6	7	8	9	10
m i , г	31,56	31,56	31,56	31,56	31,56	31,56	31,56	31,56	31,56	31,56
Серия № 1
t i , ч	0,1	0,1	0,1	0,1	0,1	0,1	0,1	0,1	0,1	0,1
E i , г	0,86	1,56	2,14	2,61	2,99	3,31	3,57	3,78	3,95	4,09
А i , г	4,86	8,84	12,10	14,77	16,96	18,75	20,21	21,41	22,39	23,20
B i , г	1,05	1,05	1,05	1,05	1,05	1,05	1,05	1,05	1,05	1,05
C i , г/кг	0,05	0,17	0,32	0,52	0,75	1,00	1,27	1,56	1,87	2,19
Серия № 2
t i , ч	0,5	0,5	0,5	0,5	0,5	0,5	0,5	0,5	0,5	0,5
E i , г	2,99	4,09	4,50	4,65	4,70	4,72	4,73	4,73	4,73	4,73
А i , г	16,96	23,20	25,49	26,33	26,65	26,76	26,80	26,82	26,82	26,82
B i , г	5,25	5,25	5,25	5,25	5,25	5,25	5,25	5,25	5,25	5,25
C i , г/кг	0,17	0,42	0,71	1,01	1,32	1,63	1,93	2,24	2,55	2,86
Серия № 3
t i , ч	1	1	1	1	1	1	1	1	1	1
E i , г	4,09	4,65	4,72	4,73	4,73	4,73	4,73	4,73	4,73	4,73
А i , г	23,20	26,33	26,76	26,82	26,82	26,83	26,83	26,83	26,83	26,83
B i , г	10,50	10,50	10,50	10,50	10,50	10,50	10,50	10,50	10,50	10,50
C i , г/кг	0,18	0,41	0,64	0,87	1,11	1,34	1,57	1,81	2,04	2,27

Оба указанных метода характеризуются выраженными отклонениями от реальной кинетики многократного приёма этанола. Особенно значительные погрешности присущи методу суммирования концентраций, который полностью соответствует физиологической кинетике только при условии следующего приёма этанола после завершения выведения из организма предыдущей дозы (см. рис. 1, 2).

Более распространённый в экспертной практике метод суммирования доз также обладает рядом существенных недостатков, продемонстрированных в рассмотренных примерах. Так, анализ кривых этанолемии наглядно показывает, что аппроксимация многократного приёма этанола путём суммирования доз допустима только при небольших промежутках времени между эпизодами употребления алкогольных напитков, не превышающих 10 минут. В противном случае результаты определения количественного содержания этанола в организме будут ошибочными для первых часов после окончания его приёма (см. рис. 1, 3).

Продолжительность периода указанных отклонений пропорциональна длительности промежутков времени между приёмами алкоголя. Так, в примере 2 продолжительность отклонения динамики этанолемии от реальной в случае её приближения однократным употреблением суммар- ной дозы водки при длительности временных промежутков между эпизодами приёма величиной 6 минут составляет 2,5 ч, а 30 минут – уже 6 ч. При увеличении указанных промежутков времени до 60 минут продолжительность отклонения аппроксимирующей кривой достигает 10 ч (см. рис. 3). Кроме продолжительности промежутков времени между эпизодами употребления алкоголя на степень расхождения кривых этанолемии при одно- и многократном его приёмах оказывает влияние величина принятых доз. Данный фактор, наоборот, характеризуется обратно пропорциональным влиянием, особенно заметным при его сочетании с большой длиной отрезков времени между эпизодами приёма алкоголя. Указанный эффект, в частности, становится заметен на графике абсорбции этанола в третьей серии десятикратного приёма (см. рис. 3).

Разработанный метод кинетического суммирования лишен недостатков обеих перечисленных аппроксимаций многократного приёма, позволяя, кроме того, учитывать возможность изменений ключевых кинетических параметров по мере употребления алкоголя. Метод кинетического суммирования потенциально может быть применён к любой кинетической модели. В рамках настоящего исследования данный метод основывался на наиболее физиологической из используемых в судебной медицине модели элиминации этанола нулевого порядка с абсорбцией и безвозвратным дефицитом абсорбции первого порядка.

Относительным ограничением разработанной кинетической модели является затруднительность определения погрешностей её результатов по величине ошибок исходных показателей, как это принято делать в случаях однократного приёма алкоголя [4, 7]. Это объясняется большим количеством исходных переменных в модели и связанными с этим техническими сложностями, а также вариабельностью вычислительного алгоритма. В этой связи возможные погрешности модели целесообразно оценивать путём использования в расчётах предельных значений наиболее важных исходных кинетических параметров: константы извлечения и скорости элиминации этанола, в качестве которых следует принимать 0,2 и 0,6 ч-1 и 0,1 и 0,2 г/(кг·ч).

Заключение

На базе кинетического уравнения элиминации нулевого порядка с абсорбцией и безвозвратным дефицитом абсорбции первого порядка разработана математическая модель кинетики многократного приёма алкогольных напитков любых объёмов и крепости, разделённых промежутками времени любой продолжительности.

Комплекс разработанных вычислительных процедур реализован в формате компьютерной программы «Alcohol Calculator V 3.0», которую рекомендуется использовать при судебномедицинской оценке количественного содержания алкоголя в организме в юридически актуальный момент времени.