Математическое моделирование кинетики однократного приема этанола

                                                           УДК 340.628:615.711.12

Актуальность проблемы экспертной оценки кинетики этанола определяется наличием установленных законодательством многих стран допустимых пределов концентрации этанола в организме при вождении автомобиля [1]. Это позволяет водителям избегать наказания, уклоняясь от забора образцов крови или иных биосред в течение нескольких часов после дорожно-транспортного происшествия. Полученная задержка в силу естественных процессов элиминации приводит к снижению концентрации этанола в организме водителя ниже допустимого законом уровня. Также водитель, в организме которого был обнаружен алкоголь, может утверждать, что в момент нахождения за рулем он был трезв, а принял алкоголь уже после дорожнотранспортного происшествия, например, для уменьшения стресса, вызванного полученными травмами [2, 3]. Подобное поведение получило название «hip-flask argument» (аргумент с фляжкой) или «cognac alibi» (коньячное алиби) [3–5].

Изложенное вызывает необходимость экспертной проверки каждой возможной версии приема алкоголя. Несмотря на то, что распределение и метаболизм этанола в организме являются сложными процессами, которые лучше всего описываются многокомпонентными кинетическими моделями, экспертные расчёты в подобных случаях по-прежнему основываются на однокамерной модели элиминации нулевого порядка, предложенной E.M.P. Widmark:

C t = C 0 ( 1 - d ) -p t , (1) где C t – концентрация этанола в крови в момент времени t , г/кг; d – относительный безвозвратный дефицит абсорбции, равный сумме удельных потерь этанола, обусловленных его метаболизмом желудочной алкогольдегидрогеназой и метаболизмом первого прохождения; β – почасовая скорость элиминации этанола, г/(кг·ч); t – время после приема алкоголя, ч; С 0 представляет собой условную величину, равную

C = —

0 rM , где m – масса принятого этанола, г; М – масса тела, кг; r – фактор редукции [6, 7].

Модель E.M.P. Widmark базируется на допущениях о мгновенной абсорбции этанола из гастроин- тестинального тракта и мгновенном его распределении в организме. Вследствие отсутствия учёта временного дефицита абсорбции параметр С0 в модели E.M.P. Widmark всегда больше, чем реальная пиковая концентрация этанола в крови. В этой связи законодательство Германии, например, предписывает исключение первых двух часов после окончания приема алкоголя из расчетов концентрации этанола [3]. Для устранения данного недостатка было предложено модифицировать модель (1) путем введения сомножителя, моделирующего кинетику абсорбции этанола первого порядка:

C t = C 0 ( 1 - e - ^y ) -e t . (2) где k a – константа абсорбции, ч^-1 [8].

Изложенное определило цель исследования – построение кинетического уравнения элиминации этанола нулевого порядка с абсорбцией первого порядка, учитывающего безвозвратный дефицит абсорбции этанола, с возможностью определения погрешностей оценки параметров модели, а также реализация модели в формате компьютерной программы.

Материал и методы исследования

Методологический дизайн исследования представляет собой аналитическое математическое моделирование кинетики однократного перорального приема этанола на основе модели элиминации нулевого порядка с абсорбцией первого порядка.

Операции математического анализа производили вручную, а также с использованием онлайн-приложения Wolfram|Alpha (https://www.wolframalpha. com). Код программы для электронно-вычислительной машины составляли на языке программирования C# с использованием бесплатно распространяемой версии приложения Microsoft Visual Studio .

E (t ) =

k a               .

С учетом безвозвратного дефицита количество этанола в организме определяется уравнением абсорбции и пресистемного метаболизма

этанола первого порядка

A = m (l- e" kat)-E (t), которое, принимая во внимание (4), следует записать как

A = m ( l- e k a t

—

k d

Константа извлечения в зависимости от сте-

Результаты исследования

Пресистемный метаболизм этанола и соответственно безвозвратный дефицит его абсорбции в рамках модели элиминации (2) может быть описан дополнительным кинетическим уравнением реакции первого порядка, в соответствии с которым скорость пресистемного метаболизма этанола пропорциональна его концентрации в содержимом гастроинтестинального тракта:

цита этанола к концу его выведения из организма прямо пропорциональна константе извлечения и

равна половине ее значения:

E m

= - kd .

2 d .

dE - k d P ^{( t} ) ,

где Е – фракция этанола, удаляемая в результате его пресистемного метаболизма, г; kd – константа извлечения, ч-1; Р – суммарное количество этанола в содержимом гастроинтестинального тракта и системе воротной вены, равное где А – количество абсорбированного этанола, г.

Поскольку в соответствии с моделью абсорбции первого порядка то количество этанола в гастроинтестинальном тракте в момент времени t после приема алкоголя определяется выражением

Отсюда, в соответствии с (3), получаем уравнение

Из выражения (5) следует уравнение периода времени, за который происходит всасывание поло-

вины количества принятого внутрь этанола:

a ad

где t 1₂ – период полуабсорбции, ч.

С учетом (5) модель элиминации этанола нулевого порядка с абсорбцией первого порядка при-

нимает вид:

C t

= С ₀ ( /- e"^kat jl-

k d

k a

-P t .

Приравняв первую производную функции (7) к нулю, можно найти время достижения пиковой

концентрации этанола в крови:

dE = kdm - kdm (l- e" kat), проинтегрировав которое, для однократного приема этанола (Е0 = 0) находим

t max

= _/|n C 0 ( k . - k d ) k .         в ’

где t max – время достижения пиковой концентрации этанола в крови, ч.

Подставив полученное из (8) значение t max в выражение (7), находим уравнение пиковой концентрации этанола в крови:

(l        в         -kd 1-

^ max — ^C 0 1    ~ (i i X ¹

V    ^C 0 ⁽ k a ^— k d ) JV     k a J           (9)

в In C 0 ( k a - k d ) k a          в ’

где C max – максимальная концентрация этанола в крови, г/кг.

Время полного выведения этанола из крови можно определить найдя корень неявной функции

0 —

m ( 1 rM

—

— kJ e ^a

—

k d k a

—в t .

Для этого можно воспользоваться итерацион-

ным алгоритмом Ньютона, в соответствии с которым

f (tn) f '(tn ) •

где

t n + 1

—

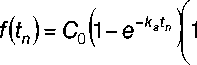
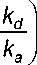
— в tn •

нола в крови и время его достижения, а также период полного выведения этанола из организма, приняв усреднённые значения фактора редукции для мужчин и почасовой скорости элиминации этанола, соответственно равные 0,7 и 0,15 г/(кг·ч).

С учётом приёма алкоголя на пустой желудок целесообразно задать значения констант абсорбции и извлечения равными 2 ч-1 и 0,2 ч-1 соответственно. Количество принятого этанола определяется объемом и крепостью алкогольного напитка:

m — Vz p , где V – объем принятого алкогольного напитка, мл; z – удельный объем спирта в напитке; ρ – плотность спирта, равная 0,789 г/мл [7]. Учитывая, что в данном примере количество принятого этанола составляет 157,8 г, в соответствии с формулами (6)–(9) находим необходимые кинетические параметры: C2 = 1,69 г/кг; tmax = 1,65 ч; Сmax = 1,71 г/кг; период полуабсорбции t1 = 0,41 ч (рис. 1). Время полного выведения этанола из крови в соответствии с численным методом Ньютона составляет 13,53 ч (табл. 1).

f'(tn) — С0 (ka — kd )e - ‘-'—в • n – порядковый номер итерации. В зависимости от принятой дозы алкоголя метод Ньютона может не сойтись при небольших начальных значениях t. Поэтому в расчётах целесообразно принять t0 = 5 ч. Использование данного численного алгоритма помогает найти время полного выведения этанола из крови с точностью до 8 знаков в дробной части результата всего за три итерации.

Обратной задачей, подлежащей разрешению экспертным путем, является определение количества принятого алкоголя по его концентрации в крови и времени, прошедшему после его приёма. Уравнение количества принятого этанола c учётом безвозвратного дефицита его абсорбции следует из выражения (7):

_{m —}    rM ⁽ C t +P t )    .         (11)

( l — e ~ ‘ a t fl — k d ¹

^V t    ‘ a J

Пример 1

Субъект мужского пола весом 100 кг принял внутрь натощак 500 мл водки крепостью 40°. Необходимо определить концентрацию этанола в цельной крови через 2 ч после приема алкоголя, период полуабсорбции, максимальное содержание эта-

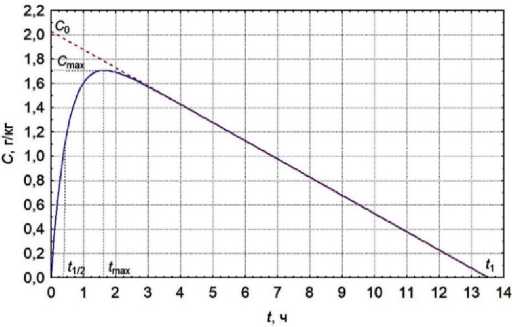
Рисунок 1. Динамика концентрации этанола в цельной крови субъекта массой 100 кг после однократного приема 157,8 г этанола. Сплошной линией показана кривая концентрации в соответствии с моделью (7) элиминации нулевого порядка с абсорбцией первого порядка, штриховой – в соответствии с моделью (1) E.M.P. Widmark. В обеих моделях относительный безвозвратный дефицит абсорбции этанола принят равным 10 %, фактор редукции – 0,7, скорость элиминации – 0,15 г/(кг·ч)

Figure 2. Dynamics of ethanol concentration in the whole blood of a subject weighing 100 kg after a single intake of 157.8 g of ethanol. A solid line shows the concentration curve in accordance with the zero-order elimination model (7) with first-order absorption, a dashed one – in accordance with the E.M.P. Wid-mark model (1). In both models, the relative irrevocable deficiency of ethanol absorption was assumed to be 10%, the reduction factor was 0.7, and the elimination rate was 0.15 g/(kg·h)

Таблица 1. Нахождение методом Ньютона корня неявной функции (10) для данных из примера

Table 1. Finding the root of the implicit function (10) by Newton's method for the data from the example

№	t 0	f ( n )	f' ( n )	f ( n )/ f ( n ) '	t 1
1	5	1,278765	–0,14981578	–8,53558305	13,53558305
2	13,53558305	–0,00148	–0,15	0,009868764	13,52571429
3	13,52571429	0	–0,15	0	13,52571429

В построенной кинетической модели погрешности измерения каждого из входных показателей приведут к погрешностям вычисляемого параметра. Эти ошибки могут быть оценены по вкладу каждого входного показателя. Условно любое из построенных кинетических уравнений можно представить в виде дифференцируемой функциональной зависимости вида p — f (x 1,..., Xn ) , где p - оцениваемый по x 1,—,xn входным показателям кинетический параметр. Тогда

рости элиминации этанола β . Частные производные функции (7) по каждой из перечисленных пере-

n Л < V	a f ( x 1 , — , x n )	A
A p — ^ i — 1	a x i	A x

где ^A p - абсолютная предельная погрешность кинетического параметра; A x — абсолютная предельная погрешность i -го показателя, выраженная в соответствующих единицах измерения.

менных равны:

8C_	^^ - ( 1- e"kat ) .		r 1-	k d )
d V	rM		V	k a ) ,
д С —	V P- ( 1- e rM	k - ' ) •	r 1-	kd. )
d z			V	k a ) ,
d С ---=	- VZ y- ( 1- rM 2	- e kat ) -		1- k d I
d M				V k a ) ,
д С —	- Vz p-(1- r 2 M	- e kat ) -		Г1- k d 1
d r				V     k a J ,
d С —— - d ka a	e - k a t Vz p rMk 2 a	- ( k 2 1 + kd ( ek a t - kat - ad   a

С — - VzPL .(1- e - kat dkd    karM da

Пример 2

Необходимо оценить погрешность определения концентрации этанола в цельной крови через 2 часа после приема алкогольного напитка для данных из примера 1 при следующих предельных абсолютных ошибках измерения входных показателей: объём напитка – 20 мл, крепость напитка – 1°, вес тела – 1 кг, константа абсорбции – 1 ч-1, константа извлечения – 0,05 ч-1, фактор редукции – 0,1, скорость элиминации – 0,025 ‰·ч-1, время после приема алкогольного напитка – 15 минут.

Символически функциональную зависимость (7) можно записать как

С — f(x 1>. x 8), где x 1,—,x8 - условное обозначение восьми физических величин: объема V и крепости z принятого алкогольного напитка, веса М субъекта, фактора редукции r, констант абсорбции ka и извлечения kd, времени t после приема напитка и почасовой ско-

ЭС   Vz р(■. - k_d ) e - ^{k a} t

--—--e d 1         rM

дС—-1

dp .

Результаты промежуточных вычислений приведены в таблице 2. Тогда предельная абсолютная ошибка определения концентрации этанола через 2 ч после его приема равна

A p — i fx i —1

1 , ^— , x 8 ) 5 x i

A _x. — 0,743

г/кг.

Анализ таблицы 2 показывает, что наибольший вклад в формирование абсолютной ошибки определения параметра C t внесли погрешности измерения фактора редукции (38,3 %) и константы абсорбции (24,9 %). Поэтому именно эти показатели должны быть определены максимально точно при оценке кинетики этанола. Суммарный удельный вклад погрешностей измерения остальных актуальных физических величин в итоговую ошибку в рассматриваемом случае составил всего 36,8 %.

Аналогичным образом формула (12) может быть обобщена на любой иной оцениваемый кинетический параметр: период полуабсорбции, пиковую этанолемию и время её достижения, период полного выведения этанола, количество принятого этанола.

Таблица 2. Результаты вычисления погрешностей параметра C t из примеров 1 и 2

Table 2. The results of calculating the errors of the C t parameter from examples 1 and 2

Параметр x i	Значение	д С д x i	A x i		д С д x i	A x i
V , мл	500	0,003983	20	0,079668
z	0,4	4,979243	0,01	0,049792
М , кг	100	–0,01992	1	0,019917
k a , ч-1	2	0,184969	1	0,184969
k d , ч-1	0,2	–1,1065	0,05	0,055325
r	0,7	–2,84528	0,1	0,284528
β , г(кг·ч)-1	0,15	–2	0,025	0,05
t , ч	2	–0,07568	0,25	0,01892

Таблица 3. Результаты вычисления погрешностей параметра m из примера 3

Table 3. The results of calculating the errors of the m parameter from example 3

Параметр x i	Значение	д c д x i	A x i		д С д x i	A x i
C t , ‰	0	77,77784	0,1	7,777784
М , кг	100	0,816667	1	0,816667
k a , ч-1	2	4,537516	1	4,537516
k d , ч-1	0,2	45,37041	0,05	2,26852
r	0,7	116,6668	0,1	11,66668
β , г(кг·ч)-1	0,15	544,4449	0,025	13,61112
t , ч	7	11,66654	0,25	2,916635

Пример 3

Необходимо определить количество принятого этанола, которое будет полностью выведено из крови через 7 ч после его приёма натощак субъектом мужского пола с массой тела 100 кг при тех же заданных кинетических параметрах, их предельных абсолютных погрешностях и предельной погрешности измерения этанолемии 0,01 г/кг.

Согласно формуле (11) масса принятого этанола в рассматриваемом примере составляет 81,7 г. Частные производные функции (11) по каждой из семи переменных равны:

д m _ rMe k a ( - 2 1 + k d ( - - a t + e^k ° t - 1 ) p t + C_t ) ) ( - . - - d ) ² -( е ^ -1 ) ²

д m_ -_arMe^-a ( p t + C_t ) д - d ⁼( - . - - d )² " ( e ‘ - ^t - 1 ) ,

д m ”ar"

m ( p t + C_t )

(1 - e

-J

kt a

,

д m     kjMe k a

a д C (ka - kd He-" - 1)

д m _      r ( p t + C t )

MM ( 1 - e - - . t ) .f i _ k d ) '

V ^-a )

д m _     - . rtMe ^- .

дР    (-. - -d)-(e-.t -1), дm _ -arMeka(p(- -at + e-at -1)- -aC)

"a "        ( -a - -d ) - ( e ^v -1 ) ²

Результаты промежуточных вычислений приведены в таблице 3.

Тогда предельная абсолютная ошибка определения количества принятого этанола равна

A m = Z i=1

d f ( x 1 , ^ , x 7 ) d x i

^A X i

= 43,6 г.

При обратных расчетах наибольший вклад в формирование итоговой ошибки вычислений вносят погрешности измерения скорости элиминации, фактора редукции и уровня этанолемии (соответственно 31,2, 26,8 и 17,8 % в рассматриваемом случае).

Для автоматизации расчётов комплекс изложенных вычислительных процедур был реализован на языке С# в виде приложения «Alcohol Calculator V 1.0» (свидетельство о государственной регистрации программы для ЭВМ № 2022669828). В зависимости от типа задачи приложение оценивает параметры кривой концентрации этанола в организме либо количество принятого этанола, а также их абсолютные предельные ошибки (рис. 2, 3).

Рисунок 2. Окно приложения «Alcohol Calculator V 1.0» с введенными в текстовые поля данными из примеров 1 и 2

Figure 2. The window of the application "Alcohol calculator V 1.0" with the data entered in the text fields from examples 1 and 2

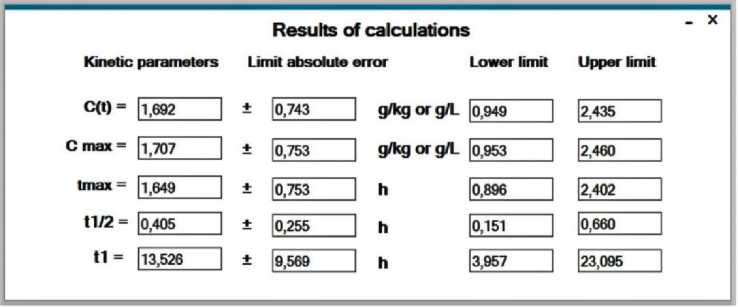
Рисунок 3. Окно приложения «Alcohol Calculator V 1.0» с итогами вычислений кинетических параметров из примеров 1 и 2 и их предельных абсолютных погрешностей

Figure 3. The application window "Alcohol calculator V 1.0" with the results of calculations of kinetic parameters from examples 1 and 2 and their maximum absolute errors

Обсуждение результатов исследования

Немаловажным результатом проведённого моделирования является реализация комплекса разработанных относительно трудоёмких вычислительных процедур в формате компьютерной программы «Alcohol Calculator V 1.0». Данное приложение не требует установки на системный диск и может запускаться со съёмных носителей даже при отсутствии у пользователя прав администратора. Для исключения проблем сходимости итерационных алгоритмов приложение содержит запрет на расчёты при приеме менее 16 г этанола. Дополнительно с помощью табличного процессора Excel построен ряд рабочих областей с введёнными в ячейки электронных матриц формулами, выполняющими автоматическое вычисление кинетических параметров и их погрешностей. Данное обстоятельство избавляет пользователей от необходимости самостоятельного выполнения трудоемких математических операций и связанных с этим вычислительных ошибок.

Заключение

• 1.    Разработана математическая модель кинетики однократного приема этанола с его элиминацией нулевого порядка, абсорбцией и пресистемным метаболизмом первого порядка.

• 2.    Предельные абсолютные погрешности кинетических параметров построенной модели могут быть оценены путем суммирования парциальных вкладов исходных физических величин.

• 3.    Комплекс разработанных вычислительных процедур реализован в формате компьютерной программы «Alcohol Calculator V 1.0», которую рекомендуется использовать при судебно-медицинской экспертной оценке острой алкогольной интоксикации.