Математическое моделирование колебаний грунта на основе учета нелинейных свойств при интенсивных воздействиях

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КОЛЕБАНИЙ ГРУНТА НА ОСНОВЕ УЧЕТА НЕЛИНЕЙНЫХ СВОЙСТВ ПРИ ИНТЕНСИВНЫХ ВОЗДЕЙСТВИЯХ

В. Б. Заалишвили, Ж. Д. Туаева

Объектом исследования является модель колебания грунтовой толщи с нелинейными свойствами при интенсивных сейсмических воздействиях, заданных в виде различных импульсов. Цель работы — создание методики определения функций смещения. Рассматривается нелинейное сейсмическое воздействие 5Я-волпы па грунтовую толщу с нелинейными свойствами. Математическая модель строится па основе нелинейной зависимости Хардин — Дрневича и представляет собой начально-краевую задачу упругости для функции смещения грунтовой толщи при известной импульсной функции. Получены решения начально-краевых задач при различных входных данных. Анализ полученных данных показывает, что при учете нелинейных свойств грунтов в математической модели колебаний грунтовой толщи в условиях значительных деформаций на графике спектральной кривой появляются пики па кратных частотах.

Нелинейная модель сплошной среды должна, учитывать две нелинейности разной природы: геометрическую нелинейность (конечность деформации) и физическую нелинейность, т. е. нелинейную связь тензоров напряжения и деформации. Применение нелинейной модели при исследовании сейсмических волн обусловлено использованием мощных электрогидравлических вибрационных источников в сейсморазведке, необходимостью расчета, интенсивных сейсмических полей при взрывах и землетрясениях, важностью учета, параметров определенного грунта. [4].

Рассмотрим слой почвы с нелинейными свойствами: 0 <  z < h, a. z > h — полупространство с линейными упругими свойствами. На слой почвы z = h действует вертикальная преобладающая SH-волна с данной частотой /о- Упругое полупространство характеризуется S-волной со скоростью распространения С_е. Поведение свойств грунта, обычно описывается зависимостью, связывающей функции деформации уД,^ и касательного напряжения тД,^ (t — время)

_т = СДДу, (1)

где ОД) — модуль упругости.

Уравнение (1) характеризует нелинейное поведение грунтов по Хардин — Дрневичу, т. е.

Gh) =

' 7о

где Go — известное максимальное значение модуля упругости для малых возмущений, 7о — заданное максимальное значение деформации.

Дополнительно к зависимостям (1)—(2) введем функцию, характеризующую нелинейное затухание, данное Е. И. Хосри (1984):

/3(7) =/3o + [/3m-/3o]r^T,                          (3)

где Ро и р_т — заданные коэффициенты затухания.

Уравнение, описывающее динамику грунтовой среды, выглядит следующим образом:

Эт р — заданная плотность грунта, a — ускорение.

Для учета нелинейности грунтов касательное напряжение представляем в виде

T = G^ + Go-Ph^-                (5)

az          az

Перейдем к задаче нахождения функции смещения upytY Принимая во внимание то, что а = ^, соотношение (4) перепишем в виде

OZ \ V              / OZ / или

+ GoPhYy- + [G(7) + СоРШтг-т.            (7)

^u 0,0015

-0,003

0,001

0,0005

-0,0005

-0,001

-0,0015

-0,002

-0,0025

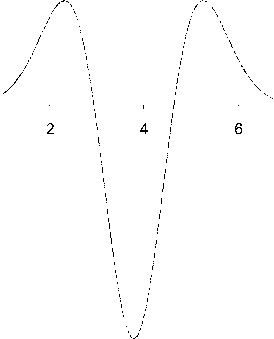
Рис. 1.

10 t, c. 12

Для последующих выкладок введем следующее обозначение:

Вопрос постановки граничных и начальных условий решается следующим образом. На границе z = h задается импульсная функция вида

Uo(t)=Uo- 7Г------- 6      °    ’                      (9)

где to — время, при котором частота колебаний принимает наибольшее значение. График функции представлен на рис. 1.

На свободной поверхности z = 0 принимаем

Эи dz

= 0.

2 = 0

(Ю)

Что касается начальных условий, то в линейно-упругой среде (полупространство z < /г) считается заданным поле скоростей. Таким образом, начальные условия запишутся в виде

и\ = 0. t=o

Эи dt

= Се. t=o

(И)

1       2       3      4       5       6       7       8       9      10      11      12      13

-0,5

Частота, Гц

Рис. 2.

Равенства (8)—(11) представляют собой начально-краевую задачу, моделирующую волновой процесс в рыхлой грунтовой среде с нелинейными свойствами. Для данной модели проведено численное исследование с применением метода конечных разностей [1]. Конечно-разностная схема модели (8)—(11) применяется для пятиточечного шаблона в расчетной точке Д^, tj), г = 0,... N, j := 0,... , М (М и N — количество узлов сетки), и выглядит следующим образом:

"Г ' - 2u^ + и^{3 1} k³_m - к³ ну. -и³ ну. - 2и³ +

р--№--= ~~ +    -- где г = 1,... , N — 1, j = 1,... , М — 1, начальные и граничные условия:

щ° _{= 0}, ^^^ = С_е, г = 1,... , N,                       (13)

<=u₀U*dt), ^£^л! = 0, j = 0,...,М.             (14)

Рассматриваемая схема (12)—(14) является явной, что следует из вида ее пятиточечного шаблона (u2+1, Ц, л)1. Ц+1, ».)|). порядок ее аппроксимации — O^dt2 + с/ж2). Введя обозначение dt2

преобразуем (12) к виду

^⁺¹ = Цхи^ + (2-х (^₊1 + Ц^Ц- Ц⁺¹ + ^₊₁ (хЦ₊?) ■       (15)

Устойчивость схемы (12)—(14) соблюдается при выполнении условия Куранта

Ц \ * dt2

На рис. 2 приведен график зависимости амплитуды функции смещения от частоты колебаний (спектр колебаний на поверхности грунтовой толщи).

u 0,02

-0,02

0,015

0,01

0,005

-0,005

-0,01

-0,015

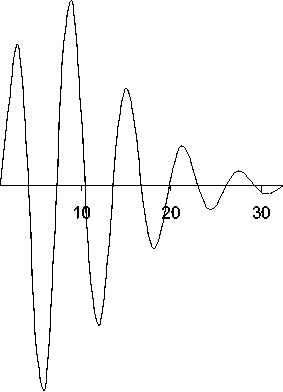
Рис. 3.

50         60 _{t, c.} 70

Анализ полученных данных показывает, что при учете нелинейных свойств грунтов в математической модели колебаний грунтовой толщи в условиях значительных деформаций на графике спектральной кривой появляются пики на кратных частотах. Полученные данные сравнивались с данными экспериментальных исследований, сопоставление показало хорошее соответствие. Таким образом, компьютерный результат может быть использован для исследований сейсмических свойств грунтов на различных глубинах.

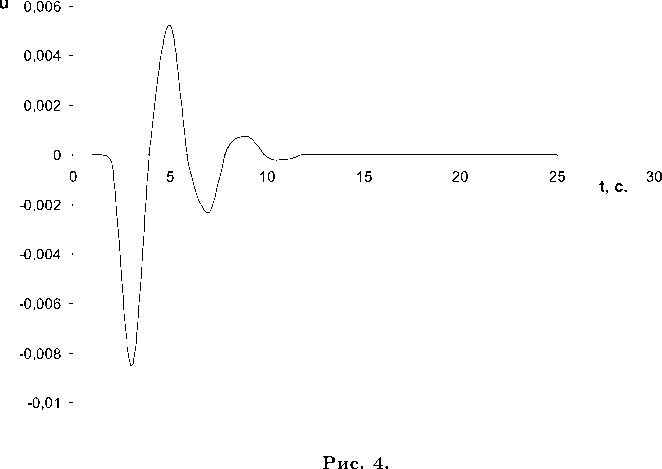
Теперь рассмотрим другие импульсные функции, в частности, функцию-импульс Берлаге (рис. 3) u^ = оДе~^ sin Wg^ и функцию-импульс Пузырева и^ = «2^ ^{/j z} sinwg£ (рис. 4 ) [3]. Тогда, применяя аналогичную методику решения задачи, получаем уменьшение количества пиков на графике спектра. На рис. 5 приводится один график, так как вновь построенные спектры колебаний на поверхности грунтовой толщи при соответствующих импульсах имеют идентичный вид, а значения амплитуд отличаются на тысячные доли.

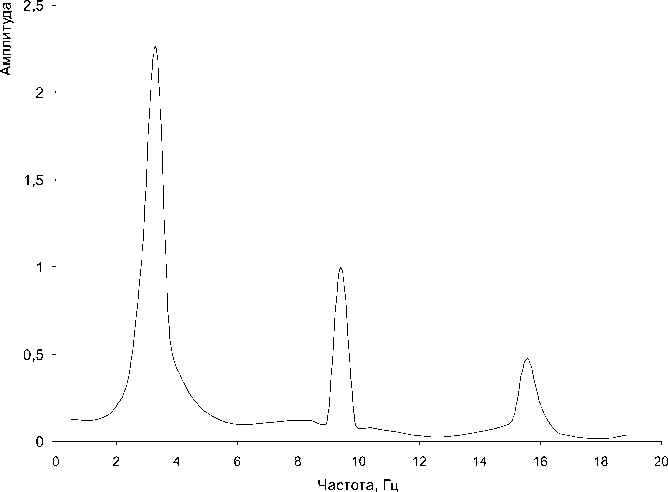
Рис. 5.