Математическое моделирование концентрационного поля электролита в управляемом электрохимическом сопротивлении
Автор: Скакунова Татьяна Павловна, Герасименко Юрий Яковлевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 1-2 (62) т.12, 2012 года.
Бесплатный доступ
Рассматривается и решается начально-краевая задача по математическому моделированию поля концентрации электролита в управляемом электрохимическом сопротивлении (УЭХС) с плоскими электродами. Модель позволяет вести полное исследование электрохимических процессов во всём объёме УЭХС. Выполнены контрольные расчёты пространственно-временного распределения концентрации при постоянном управляющем токе УЭХС.
Краевые условия, параболическое уравнение диффузии, плотность электрического тока, распределение концентрации, дифференциальное уравнение, изображение концентрации
Короткий адрес: https://sciup.org/14249766
IDR: 14249766 | УДК: 519.63(075.8)
Текст научной статьи Математическое моделирование концентрационного поля электролита в управляемом электрохимическом сопротивлении
Введение. УЭХС представляет собой цилиндрический проводник длиною / прямоугольного сечения (подложка) ахг, изготовленный из стеклографита. Если на боковую поверхность УЭХС наносить электрохимическим способом тонкий слой металла, то сечение слоёного проводника будет увеличиваться и его проводимость возрастёт. Распределение слоя осаждаемого металла по боковой поверхности УЭХС полностью определяется распределением концентрационного поля электролита.
В статье рассматривается постановка и решение начально-краевой задачи для пространственно-временного распределения концентрации электролита в УЭХС.
Основные допущения:
-
- лимитирующей стадией электродных процессов в цепи управления УЭХС является молекулярная диффузия;
-
- коэффициент диффузии электролита есть величина постоянная и не зависит от тем-
- пературы;
-
- плотность электрического тока по поверхности управляющего электрода распределена
равномерно;
-
- пространственно-временное распределение концентрации электролита является плоско параллельным и зависит от координат х, у и времени t,
-
- толщина наносимого металла значительно меньше поперечных размеров УЭХС.
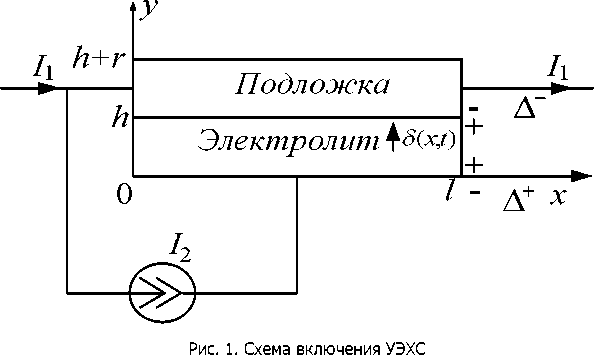
Постановка задачи. Согласно принятым выше основным допущениям, все физические поля в УЭХС являются плоскопараллельными и не зависят от координаты г(рис. 1), перпендикулярной плоскости хОу. Слой металла, наносимый на подложку УЭХС, является ничтожно тонким по сравнению с геометрическими размерами самой подложки и толщиной слоя электролита.
На основании 2-го закона Фика относительно концентрационного поля электролита С(х, у, t) ставится следующая начально-краевая задача.
^ = d(^ + ^\ хе[0;/], у е[О;Л].(1)
dt \эх 8У У
С(х;у;О) = Со,(2)
^;o:t),Ml,(3)
Эуv ' al
—(x;h;tA = N5(x;tV(4)
^(°^'f) = 0'(5)
—(/;y;f) = O, Эхv ’
где D — коэффициент диффузии электролита; G — начальная концентрация электролита; а — толщина УЭХС; б(х;Г) — неизвестное и подлежащее определению распределение плотно' сти тока на подложке; /V—электродно-кинетическая константа.
Задачу (1) — (6) удобнее всего решать операторным методом Лапласа. Для этого введём следующие соответствия:
C(x;y;f) ,= С(х;у;р); I2(t) .= Цру, 5(x;y;ty= Ь(х;у;ру
В пространстве изображений относительно С Ус,у,р^ имеем краевую задачу: pC(x;K;p)-C,=D^ + ^, (7)
QC, „ х №г (р) —(х;0;р\ =— Qyv ’ а!
—(x;h;pA = Nb(x;pV QyV '
|£(0;у;р) = 0, Qxv’
^l;y;p> = Q. Qxv’
Преобразуем уравнение (7) к виду:
с1 С Q4 Со
Qx7 ду7 D D
(Ю)
(И)
Краевую задачу (8) — (12) будем решать методом разделения переменных. Для этого введём новую функцию й(х;у;р^ по правилу:
й(х;у;р^ = С(х;у;р^—^.
Для неё получается вспомогательная краевая задача:
#й с2й р . „ DU ~ '
м^.др^УЦе!, Qyv 7 а/
—(x;h;p\ = N5(x; pY
QyV ' v
—(0;y;p) = 0, Qxv ’
QU n
—(/;y;p) = 0.
Qxv 7
Общее решение уравнения (14) определяем как суперпозицию частных режимов [1]:
и
£
Л
к
где р^ = ^, к = 1,2,... — собственные числа краевой задачи (14) — (18),
cos^x, /с = 1,2,... — собственные функции, Мп(р\, Nn(p\, МЛрА, NAp} —
/ ' ' ' * « ' и У* 7 и У* 7 К У* 7 К У* 7
произвольные постоянные.
Для конкретного определения коэффициентов разложения в (19) продифференцируем его по у.
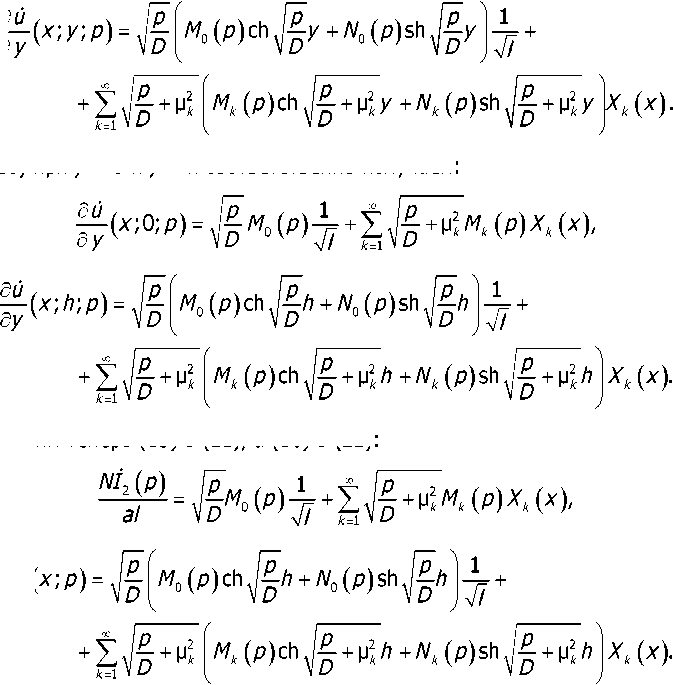
Из (20) при у = 0 и у = /?соответственно получаем:
Подставим теперь (15) в (21), а (16) в (22):
Применяя к (23) стандартную процедуру поиска коэффициентов разложения Фурье, по лучаем:
Мр) = ^7=
Мк^ = 0,к=1, 2,...
Разложение (24) с учётом (25) и (26) принимает вид
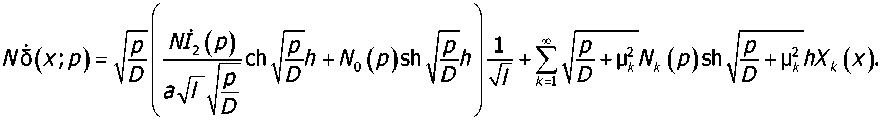
Из (27) с использованием выше приведённой процедуры поиска коэффициентов имеем:
Ро (Р)-/V0(p) = /V------г где неизвестные коэффициенты разложения Р0(р),р^(р) в ряде Фурье неизвестной плотности тока б(х;р) определяются соотношениями:
/ р, (р)=[б(х;р)ХДр)о!х.
О
о
Эти коэффициенты могут быть найдены только в результате совместного рассмотрения концентрационного и электрического полей в УЭХС, что будет сделано далее.
Подставим найденные коэффициенты Мо (p),N0 (р) и Nk (р) в выражение (19).
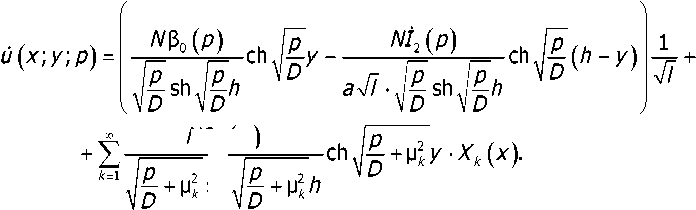
sh
/УРДР)
Подставляя выражение (28) в (13), находим аналитическое описание концентрационного поля электролита.
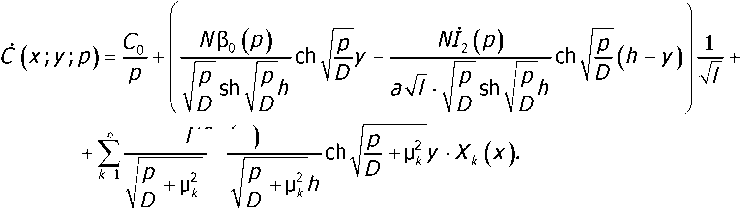
sh
/УРДР)
С помощью полученной формулы (29) можно на данном этапе получить явное выражение для расчёта концентрационного поля лишь при равномерном распределении плотности тока на подложке, когда
Цх‘.р>=Ц^-.
а разложение этой плотности в ряд Фурье
/ Г п\ f a! ^=о приводит к таким результатам:
Мр) = °, к = 1,2,.
Подстановка (31) и (32) в (29) окончательно определяет концентрационное поле элек тролита при равномерном распределении плотности тока
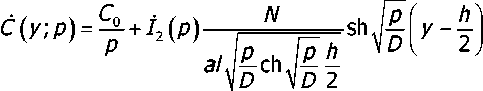
При включении входной цепи УЭХС на постоянный ток /0
Подставим (34) в (33).
= z х Со т N .
С (у; р) = + /0----, sh
Р . о . о h
Для обращения С (у;р^ рассмотрим вспомогательные функции:
sh
рЛу.р^—.
h '
Для поиска оригинала ^(у;Ц .= F\(y;p) найдём вначале полюса Р^у.ру Очевидно, что число р = 0 не является таким полюсом. Эти полюса определяют из условия
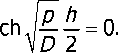
Для решения уравнения (38) введём новую переменную z по правилу
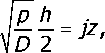
где j = V-1. Подставим (39) в (38). Получим уравнение ch jz = 0, которое равносильно урав нению cosz = 0.
Корни последнего уравнения имеют вид zk =(2/г + 1)-, k^Z
Подстановка (40) в (39) определяет полюса Рх (у,р)
Рк
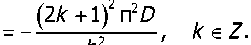
Далее находим вычеты
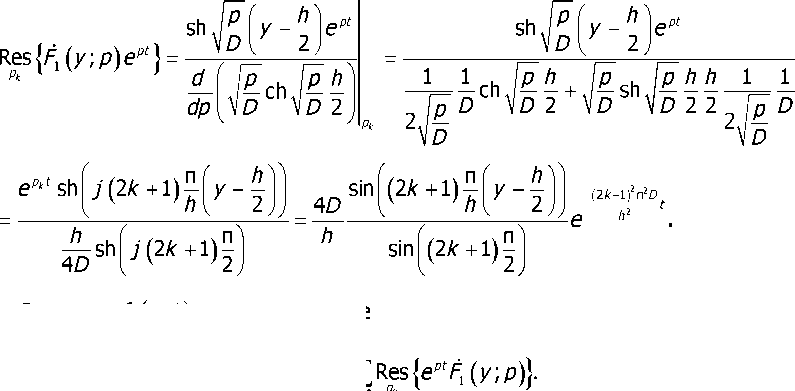
Рк
Оригинал fY (y.t) находят по схеме
Запись (42) в развёрнутом виде даёт такой результат:
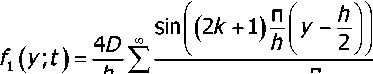
sin(2A- + l)|
(■Zk+lfrfD е Л2 f
к-0
Оригинал f2 (у;Ц .=' А2 (у;р) находят, интегрируя (43) по времени в пределах от 0 до t
4h 00 * h\ 2
—-—-- п (2^ + 1) sin(2A7 + l)^
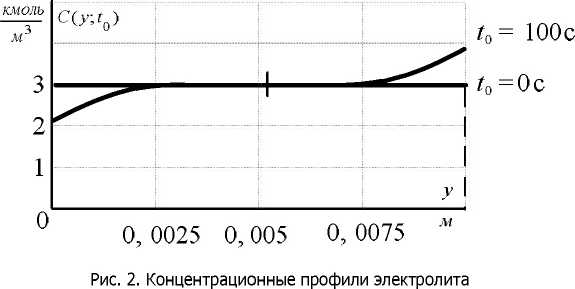
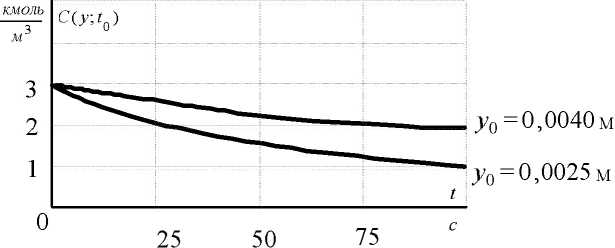
(2 1-е 1 Оригинал концентрации С(у;Г)связан с f2(y;f) соотношением C(y;f) = C0 +70^-f2(y;f). Подставим (44) в (45). 00 ' /7 2 с (у, t) = со -у—10 ^ - — па/ к=° (2А- + 1) sin(2A- + l)^ 1-е ' Полученное выражение для С(у, t) позволяет с любой степенью точности построить поверхность изменения концентрации электролита в УЭХС. При расчётах по последней формуле бесконечный ряд заменяется конечной суммой. Число слагаемых М в ней задаётся погрешностью расчёта концентрации △. Обозначая разницу между точным значением концентрации и приближённым символом RM, получим: Потребуем, чтобы №△■ (48) Рассмотрим вспомогательный ряд AhNт1 п2а/ °Й(2А- + 1)2" AhN ” 1 Между его остатком QM = —:—L У ------- и RM существует соотношение |/?J п а/ k мл (2к +1) Поэтому, если выполнить условие QM< Д, то с гарантией будет выполнено и требование (48). Для остатка QM справедлива интегральная оценка [2]: Число Мопределяется как решение неравенства 4/7/V п2а/ При исходных данных h = 0,01 м; а = 0,015 м; / = 0,08 м; Ь = 0,2 А; Со = 3 кмоль/м3, /V = 5,45 (кмоль/м3)м"А-1; Д = 1-10 3 кмоль/м3 были рассчитаны концентрационные профили С (у, 6) (см. рис. 2) и временные зависимости С(у0; t) (рис. 3) соответственно при фиксированных й и у0. Рис. 3. Временные зависимости концентрации электролита Заключение. Полученная математическая модель концентрационного поля электролита в УЭХС успешно может быть использована для расчёта режимов электрохимического осаждения металла на его боковую поверхность. Сопряжение этой модели с описанием электрического поля позволяет получить математическую модель УЭХС как элемента электрической цепи.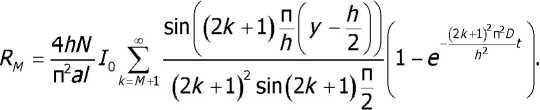
M.
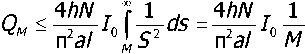
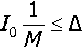
Список литературы Математическое моделирование концентрационного поля электролита в управляемом электрохимическом сопротивлении
- Полянин, А. Д. Справочник по линейным уравнениям математической физики/А. Д. Полянин. -Москва: Физико-математическая литература, 2001. -576 с.
- Градштейн, И. С. Таблицы интегралов, сумм, рядов и произведений/И. С. Градштейн, И. М. Рыжик. -Москва: Наука, 1971. -1008 с.


