Математическое моделирование критических состояний тонкостенных цилиндрических оболочек при внутреннем давлении и осевом сжатии

Введение. Хорошо известно влияние двухосного нагружения стенок труб магистральных трубопроводов [1, 2] на критическое давление в них. Двухосное нагружение вызывается осевой нагрузкой на трубу. В некоторых случаях осевая сила, возникающая вследствие особых, иногда нештатных условий функционирования трубопроводов (при резких колебаниях температуры, под водой, в местности с подвижными грунтами, в горных условиях, в районах с высокой сейсмической активностью [3, 4]), приводит к осевым напряжениям ^ , противоположным по знаку кольцевым напряжениям ст₂, порожденным внутренним или внешним давлением. Влияние коэффициента двухосности нагружения трубы m = ст _х/ о ₂ на несущую способность трубопроводов изучалось в работах [5–13] и др. В работах [8–13] критическое состояние тонкостенной цилиндрической оболочки (ТЦО) из упрочняемого материала определялось на основе критерия Свифта– Марциньяка (СМ) потери стабильности пластического деформирования ТЦО [14-16] . В указанных работах не рассматривались случаи, когда осевые и кольцевые напряжения имеют разные знаки, т. е. когда m <  0.

Критическим состоянием (состоянием предразрушения) назовем состояние ТЦО, при котором деформирование всей оболочки или ее локального участка происходит без возрастания внешней нагрузки с неконтролируемой скоростью [16]. Как известно [16], существует два вида критического состояния тонкостенной цилиндрической оболочки из упрочняемого материала: общая (тотальная) потеря стабильности процесса пластического деформирования (ОПС) и локализация пластической деформации (ЛПД) в форме кольцевой шейки или продольной выпу-чины или вмятины. Какое из этих состояний реализуется, зависит от условий нагружения [10; 11, с. 25–27; 12, с. 28–30; 16]. Для нахождения критических интенсивностей деформаций и напряжений, соответствующих как ОПС, так и ЛПД, в работе применяется критерий Свифта [14] (использованный также Марциньяком [15]).

Цель работы – нахождение аналитических выражений для критических напряжений и деформаций стенок ТЦО, в том числе труб большого диаметра, критических давлений и осевых нагрузок на ТЦО, в зависимости от механических и геометрических параметров оболочек в условиях внутреннего давления и осевой сжимающей силы (кольцевые напряжения в стенках ТЦО положительны, осевые напряжения отрицательны). Предполагается, что диаграмма деформирования аппроксимируется показательно-степенной зависимостью (6) (см. ниже).

Обозначения и допущения. Пусть 71, 72, 73 (81,82,83) - осевые, кольцевые и радиальные нормальные напряжения (логарифмические деформации) в стенке ТЦО соответственно, p – внут- реннее или внешнее давление на ТЦО, N – осевая растягивающая или сжимающая сила, m = 7 / 7 - коэффициент двухосности нагружения стенки ТЦО. Для упрощения формул используется обозначение: 5 = 4m2 - m +1. Всюду в работе нижний индекс cr указывает на критическое значение данной величины.

Предполагается, что материал оболочки однородный, изотропный, упругопластический, в пластической зоне упрочняемый, а также, что выполняется «гипотеза единой кривой», т. е. диаграмма деформирования упрочняемого материала ТЦО имеет вид:

7 = f (8), (1)

где 7 , и 8 i - интенсивности напряжений и деформаций в стенке оболочки. При условии 7 3 = 0 (см. ниже (3)) о и 8 вычисляются по формулам соответственно:

⁷ i

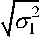
2  22

- 7i72 + 72, 8i=^ 88' + 8182 + 82 .

В работе рассматриваются следующие основные параметры ТЦО, в том числе бесшовной трубы большого диаметра.

Геометрическими параметрами ТЦО являются ее внутренний радиус R и толщина стенки t .

В начальный момент нагружения R = R 0 , t = t 0 .

Параметры, определяющие механические свойства материала ТЦО: 1) предел прочности

(временное сопротивление) материала оболочки 7 B ; 2) параметры, определяющие зависимость

(1): n и a (см. ниже (6)).

Главные напряжения в стенке ТЦО рассчитываются по формулам [17, с. 220]:

Rp N      Rp

2t  2nRt        t где 71, 72, 73 - осевые, кольцевые и радиальные нормальные напряжения в стенке трубы соответственно, p – внутреннее или внешнее давление, N – осевая растягивающая или сжимающая сила, t и R – толщина стенки и радиус оболочки. Из условий несжимаемости и пропорциональности девиаторов напряжений и деформаций, а также условия 73 = 0 следует [8-12]:

(2 - m ) 8 1 = (2 m - 1) 8 2 . (4)

Отсюда видно, что при m < 0,5 деформации 81 и 82 имеют разные знаки. Предполагаем, что внешняя нагрузка происходит по зависимости, при которой коэффициент двухосности нагружения стенки ТЦО m = 71/ 72 не изменяется в процессе нагружения. Всюду в работе будем считать, что m = 71/ 72 = const < 0.

Ситуация, когда m >  0, подробно исследовалась в работах [8-13, 16]. В случае, когда m <  0, некоторые результаты сформулированы в [18].

Аппроксимация диаграммы деформирования. Во многих работах диаграмма деформирования (1) аппроксимируется степенной функцией

7 i = А 8 П ,   A = e n n ^{- n} 7 _B .                                  (5)

Тогда материал оболочки характеризуется параметром n – показателем упрочнения материала. Известны и применяются другие аппроксимации [17, 18]. В работе будет рассматриваться более общая, чем (5), показательно-степенная аппроксимация функции (1) [8–10; 12, c. 27–30].

7 i = А 8 П exp ( a 8 i ) ,   A = ( 1 - a ) n e n n ^{- n} 7 _B                           (6)

Дильман В.Л.          Математическое моделирование критических состояний тонкостенных цилиндрических оболочек при внутреннем давлении и осевом сжатии с двумя параметрами, определяющими процесс деформирования упрочняемого материала. Коэффициент A в формуле (6) вычислен с применением критерия СМ [12, c. 27–30]. Аппроксимация (6) имеет два важных преимущества по сравнению с другими (некоторые из них приведены в [12, с. 23–24]) – она, во-первых, является обобщением и, следовательно, уточнением аппроксимации (5) и, во-вторых, она мультипликативна («удобно логарифмируется»), что желательно при использовании критерия СМ для получения обозримых аналитических зависимостей (в противном случае получаются не явные зависимости, связывающие критические значения деформаций, напряжений, давлений и т. д. с механическими и геометрическими параметрами оболочки или другой конструкции, а трансцендентные уравнения для нахождения искомых величин).

Чтобы аппроксимировать реальные соотношения между ε i и σ i , функция (1) вида (6) должна быть выпуклой вверх по крайней мере на участке, соответствующем условию c i ^G[ 0; ( c ) _cr ] . Используя полученные ниже формулы (9)–(11), средствами элементарного анализа можно доказать следующее утверждение.

Предложение 1. Если a <  0, то функция вида (6) выпукла вверх на участке, соответствующем условию c i е^ 0; ( c i )_cr J . Если a >  0, то для выпуклости вверх функции вида (6) на этом участке необходимо и достаточно, чтобы, при осевом сжатии и внутреннем давлении, выполнялось условие: 0 <  a <  1,5(1 - Пл ) [s , если - 1 <  m <  0,5, и условие: 0 <  a <  (1 - ml 2)(1 - Пл )/ s , если m < - 1.

Аппроксимация методом наименьших квадратов по формуле (6) известных, полученных в натурных экспериментах (см. ссылки в работах [11, с. 22–24; 19, 20]) зависимостей для низкоуглеродистых сталей показала [21] выполнение условий предложения 1 для параметра a .

Метод исследования . Как было отмечено, критическое состояние ТЦО может проявиться как в форме общей потери стабильности процесса пластического деформирования (ОПС), так и в форме локализации пластической деформации (ЛПД) в виде кольцевой шейки или продольной шейки либо выпучины.

На основе сравнения скорости роста интенсивности напряжений, связанных со свойствами материала, определяемыми его диаграммой деформирования, со скоростью роста интенсивности напряжений, определяемой изменением геометрии оболочки, критерий СМ позволяет вычислять критические деформации ТЦО, соответствующие той или иной форме потери оболочкой пластической стабильности. Как следствие, это дает возможность вычисления критических напряжений, давлений, осевых нагрузок при данных геометрических и механических параметрах ТЦО и условиях нагружения.

Основные результаты. Подходы работ [8–13], основанные на применении критерия СМ, с использованием зависимостей (2)-(4), и при условии c < 0 позволяют найти выражения для вычисления критических значений интенсивностей деформаций. Считаем, что на ТЦО действуют осевое сжатие и внутреннее давление. В [18] показано, что в случае ОПС sRP  ( 3  )

ci= -—expI —£i I ,(7)

t0       v 2 s а в случае ЛПД sRp   (2 - m)

ci= -—expI -y— Si I.(8)

t0       v 2 s)

Приравнивая дифференциалы выражений для c i из формул (6) и (7) в случае ОПС, и из формул (6) и (8) в случае ЛПД (критерий СМ), получим критические выражения деформаций s _itot и s iioc при реализации случаев ОПС и ЛПД соответственно. Очевидно, что s _icr = min( s i _tot , s i i _oc ). Используя это и сравнивая выражения в (7) и (8), получим

Предложение 2. Пусть ТЦО подвержена внутреннему давлению и осевой сжимающей силе. Тогда: 1) критическое состояние ТЦО возникает в виде ОПС, если - 1 <  m <  0,5, и в виде ЛПД -продольной выпучины, если m < - 1; 2) критическая интенсивность деформации вычисляется по формуле:

2 sn

----------, если m <- 1;

( e )

i cr

2 - m - 2 as

-------, если - 1 <  m <  0,5.

L 3 - 2 as

Подставляя выражения для вычисления ( e i ) _г из (9) в (6), получим

Предложение 3. В условиях осевой сжимающей силы и внутреннего давления критическая интенсивность напряжений вычисляется по формулам: при m <- 1

icr

A      I 2 - m

2 ( 1 - a ) s exp I -------------

V 2 - m - 2 as

2 - m - 2 as

n

^ в ,

при - 1 <  m <  0,5

^ icr

I 3

2 (1 - a) s exp ------- v          ( 3 - 2 as

3 - 2 as

n

^CT B .

Подставив вместо ст, его критические значения (10) и (11), а вместо е, его критическое значение (9) в формулы (7) и (8) соответственно, найдем давление p_cr в ТЦО в критический момент нагружения.

Предложение 4. В условиях осевой сжимающей нагрузки и внутреннего давления критическое давление вычисляется по формуле:

P er =

1 - a

1 - 0,5 m - as

n

t

—— cr_R, если m <- 1; n^B

1 - a ^ n    t ₀

1,5 - as ) s ^{1 -} ”.

ct _b , если - 1 <  m <  0,5.

Пусть pw – рабочее давление в трубопроводе. Обращая формулу (12), получим критическую толщину стенки tcr трубы, работающей в составе трубопровода, в зависимости от условий на- гружения, которые характеризуются параметром m .

Предложение 5. В условиях осевой сжимающей нагрузки и внутреннего давления критическая толщина стенки трубы вычисляется по формуле:

t cr

n

1-n I 1 - 0,5 m - as ] Rpw s IiI                 ,

V 1 - a )    ct _b

если m < - 1;

1 - n

1,5 - as

1 - a

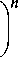
R ₀ p_w

^B ’

если - 1 <  m <  0,5.

Вычислительные эксперименты. Графики зависимостей от условий нагружения (параметра m ) критического давления pcr , критической толщины стенки трубы при данном рабочем давлении pw приведены на рис. 1 и 2. На рис. 1 предполагается ств = 600 MPa, R0 = 300 мм, t = 10 мм. На рис. 2 ств = 600 MPa, R0 = 300 мм, рабочее давление принято pw = 8 MPa. На рис. 1 кривые расположены снизу вверх в таком порядке: при m* < m < 0 (число m * определено в (14)) первые три линии - n = 0,2, a = 0,2; 0; -0,2 соответственно; следующие три линии - n = 0,1, a = 0,2; 0; - 0,2 ; при m < m* порядок кривых противоположен. На рис. 2 порядок расположения кривых противоположен их порядку на рис. 1.

Заметим, что при

m* = 1-^ ^ 0,725

формула (12) упрощается, становится независимой от n и a и приобретает вид:

2 t

P er = T° ° b .

3 R ₀

При условии (14) формула (13) также упрощается, становится независимой от n и a и приоб- ретает вид:

3 R 0 p v

2^B tcr

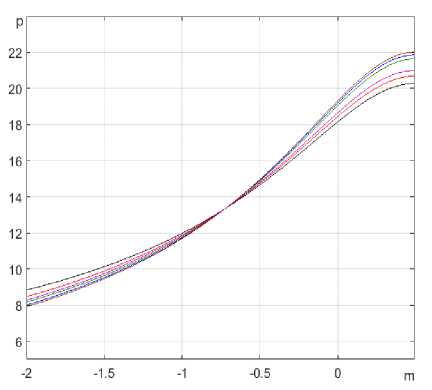
Рис. 1. Зависимость критического давления p

(в MPa) от условий нагружения (параметра m = ^ / сг2 ), при различных значениях параметров упрочнения n и a , вычисленная по формуле (12)

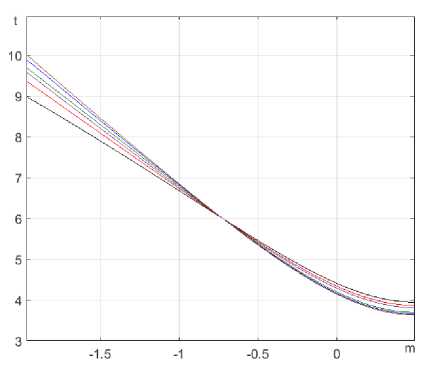
Рис. 2. Зависимость критической толщины стенки t

(в мм) от условий нагружения (параметра m = ^ / с г ₂ )

при различных значениях параметров упрочнения n и а и рабочего давления pw = 8 MPa , вычисленная

по формуле (13)

Заключение . Получены зависимости критических деформаций, напряжений и давлений от геометрических параметров ТЦО t и R , механических характеристик a _B , n и а материала ТЦО и условий нагружения, характеризующихся отношением m = ^ / ст₂ осевых и кольцевых напряжений при его постоянном отрицательном значении в условиях осевого сжатия и внутреннего давления. Установлены зависимости критической толщины стенки t_cr трубы, работающей в составе трубопровода, от условий нагружения, которые характеризуются параметром m .

Установлено, что в случае осевой сжимающей нагрузки и внутреннего давления:

• 1.    Осевые напряжения самым существенным образом влияют на величину критического давления (см. рис. 1). Из рис. 1 видно, что, в зависимости от значений параметров n и a при отсутствии осевых напряжений критическое давление примерно в 1,585…1,635 раза выше, чем при условии, когда осевые и кольцевые напряжения (по модулю) совпадают.

• 2.    Осевые напряжения самым существенным образом влияют на критическую толщину стенок (см. рис. 2).

• 3.    Критическое состояние возникает в виде: общей потери устойчивости процесса пластического деформирования при условии - 1 <  m <  0,5 и в виде локализации пластической деформации - продольной выпучины, при условии -да <  m < - 1.

• 4.    Влияние параметров упрочнения n и a в предложенном диапазоне на критическое состояния ТЦО не очень существенно (см. рис. 1, 2), но заметно. Например, при n = 0,2, а = 0,2 критическая толщина стенки при данных условиях t_cr = 9 мм , а при n = 0,1, а =- 0,2, t_cr = 10 мм .