Математическое моделирование методики установки стента из материала с памятью формы при проведении эндобилиарных вмешательств

Медицинские аспекты применения стентов в хирургии гепатобилиарнодуоденальной зоны

Стентирование – мини-инвазивное внутрипросветное хирургическое вмешательство, проводимое с целью установки стента – специального полого каркасного устройства, которое помещается в просвет полых органов человека (коронарных сосудов, желчных протоков и т.д.) и обеспечивает проходимость и расширение участка, суженного патологическим процессом [17]. Стентирование нашло широкое применение в разных направлениях медицины – чаще всего этот метод используют для восстановления кровотока в крупных сосудах (артериях), которые питают сердце насыщенной кислородом кровью [33].

Различные методы стентирования стали применять в гепатологии и гастроэнтерологии – в частности, для восстановления просвета желчевыводящих путей [20]. Сужение просвета желчевыводящих протоков на различных уровнях, как и их непроходимость, может наблюдаться при различных заболеваниях, включая злокачественные опухоли печени и поджелудочной железы. В результате такого сужения может развиться холестаз – нарушение оттока желчи, чреватое появлением механической желтухи, развитием холангита – воспаления желчных протоков – и других тяжелых последствий [15, 26]. Стентирование желчевыводящих путей – процедура достаточно сложная, так как при ее проведении обычно используется специальная система, состоящая из проводника, катетера и собственно стента.

Эндоскопическое лечение стенозов желчных протоков основано на использовании пластиковых или саморасправляющихся металлических стентов (рис. 1). Билиарное стентирование производится при доброкачественных и злокачественных стенозах общего желчного протока у части пациентов с высоким операционным риском или у пациентов с невозможностью выполнить радикальную операцию (метастазы/местная инвазия) [29].

Первые эндоскопические вмешательства на большом дуоденальном сосочке (рис. 2) были выполнены в 1974 году K. Kawai в Японии [18] и M. Classen в Германии [13].

Применение эндоскопического стентирования панкреатического протока при помощи пластиковых стентов для лечения или профилактики острого панкреатита было рассмотрено в работах [11, 30, 31]. В статье [8] выполнено транспапиллярное стентирование желчевыводящих путей при доброкачественной опухоли панкреатобилиарной области, что позволило: ликвидировать или уменьшить болевой синдром; привести к норме биохимические и лабораторные показатели крови и мочи; предупредить развитие постманипуляционного панкреатита; подготовить больных к последующему оперативному вмешательству.

В работе [1] представили результаты лечения 13 пациентов с доброкачественными поражениями внепеченочных желчных протоков. Во всех случаях в область сформировавшихся стриктур (сужений) и послеоперационных дефектов желчных протоков антеградным доступом под ультразвуковым и рентгентелевизионным контролем успешно имплантированы эндобилиарные стенты различных модификаций. Средняя продолжительность функционирования имплантатов составила 18 месяцев, максимальная – 48 месяцев.

Рис. 1. Коммерческий стент из сплава с памятью формы для эндобилиарных вмешательств

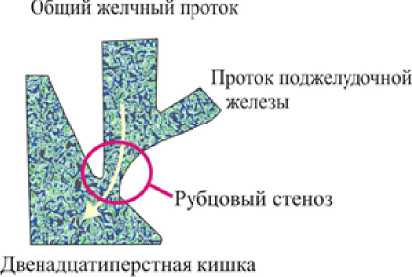
Рис. 2. Рубцовый стеноз большого дуоденального сосочка

Оценка эффективности эндоскопического билиодуоденального с т ентирования в лечении больных с опухолевой и послеоп е рационной рубцовой стриктурой внепеченочных желчных протоков рассмотрена в работе [10]. Результат ы показали, что при рубцовых послеоперационных стриктурах данный метод может служить альтернативой хирургической операции, а при опухолевых стриктурах – средством подготовки к операции или окончательным вариантом терапии.

Одной из основных проблем стентирования остаётся перфораци я (механич е ское повреждение) тканей при раскрытии стента. Так и м образом, целью работы является разработка, развитие и усовершенствование мет о дики установки стента с памятью формы в желчный проток при рубцовом стенозе на основе м атематического моделирования, что позволит объективизировать л ечение и повысить к ачество ж изни пациента при проведении эндобилиарных вмешательств.

Биомеханические аспекты применения стентов

Биомеханические свойства нитиноловых стентов и их взаимодействие со стенками каналов являются основными темами, ра с сматриваемыми в биомеханической литературе. Изучению свойств и характеристик нитиноловых стентов посвящены экспериментальные работы [14, 16, 28]. Следует отметить, что в данных ра б отах отражены результаты механических испытаний стентов, вопросы биосовместимости и анализ гистологических свойств протоков после имплантирования. Однако данные исследования проводились лишь для кардиологических стентов: результатов исследования эндобилиарных стентов в доступн о й авторам литературе найдено не было. Конечно-элементным расчётам стентов из с п лавов с памятью формы посвящены работы [12, 22, 25, 35]. Следует отметить, что в них не учитывается процедура имплантации в сосуд. Более полные модели, связанные с вопросами имплантации, можно найти в работах [27, 32, 34]. Вышеуказанные модели основаны на конечноэлементных моделях (неаналитических), что, в свою очередь, не всегда удобно в хирургической практике, в них не рассматриваются вопросы управления напряжениями в стенке протока, которые играют огромную роль и, что также очень существенно, не изучен вопрос об управлении формой стента и напряжениями, создаваемыми стентом за счёт памяти формы.

Решение задачи управления, отраженное в д анной статье, позво л ит опред е лить параметры предоперационной обработки стента, которые обеспечат правильную форму сосуда после имплантации стента и обеспечат д опустимый уровень напряжений в ткани.

Несмотря на относительные успехи в применении таких устройств, данное эндобилиарное вмешательство не всегда успешно, поскольку врачи учитывают лишь субъективный опыт, а полных биомеханических моделей, которые могли бы количественно оценить эффективность данной хирургической операции, нет. Таким образом, целью работы является разработка, развитие и усовершенствование методики установки стента с памятью формы в желчный проток при рубцовом стенозе на основе математического моделирования с учётом определяющих соотношений, описывающих поведение материала с памятью формы, что позволит объективизировать лечение и повысить качество жизни пациента при проведении эндобилиарных вмешательств.

Постановка и решение задачи об установке стента

ИЗ МАТЕРИАЛА С ПАМЯТЬЮ ФОРМЫ

Модель системы «стент – проток»

В качестве простейшей модели системы «стент – проток» примем соосные цилиндры (рис. 3), механическое поведение которых соответствует законам теории упругости. Оценим риск возникновения разрушений в этой системе в процессе расширения просвета протока. Решение данной задачи разделим на две составляющие. Первая часть (задача 1) посвящена процедуре предоперационной подготовки стента и будет заключаться в установлении связи между деформацией стента с эффектом памяти формы и давлением, приложенным к его внешней поверхности. Вторая часть (задача 2) будет посвящена определению напряжённо-деформированного состояния внешнего цилиндра (протока) после расширения в нем стента.

Постановка и решение задачи 1

Для решения первой части задачи рассмотрим внутренний цилиндр без учёта внешнего. Допустим, что диаметр протока, необходимый для нормальной работы билиарной системы, равен 2 R ₀ . Данному значению должен соответствовать начальный внешний диаметр недеформированного стента. Путем приложения давления p к внешнему контуру стента в аустенитном состоянии можно добиться его сжатия на необходимую величину u 0 . При этом если диаметр отверстия стенозированного протока принять равным 2 R C , то и 0 = R 0 - R C . Далее стент имплантируется в проток без натяга и после нагрева расширяется до начального состояния, увеличивая просвет протока (рис. 4).

Определим зависимость p от u 0 на внешнем контуре стента. В полярных координатах постановка задачи содержит следующие уравнения.

Уравнение равновесия:

d с r + ^ r + ° е = 0

dr r

Выражение для полных деформаций, записанное с использованием закона Гука:

eph    eph

°r °r + °r , °е   °е + °о где °r, °е, °rph, °e,h — компоненты тензоров упругих и фазовых деформаций.

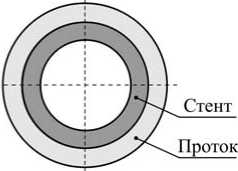
Рис. 3. Система «стент – проток»

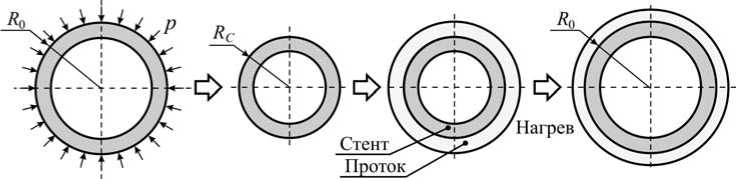
Рис. 4. Схема установки и поведения стента с памятью формы в желчном протоке

Соотношения Коши:

Граничные условия:

д ur sr = ~ , £е д r

ur r

О r ( r = r i ) = - p , C r ( r = ^r 2 ) = 0,

где r 1 и r 2 – внешний и внутренний радиусы цилиндра.

Определяющие соотношения модели А.А. Мовчана для прямого мартенситного перехода [7]:

дг ph = ( c 0 s r + a 0 s ph ) d q , дs p^h = ( c 0 s _e + a 0s^p₈ ^h ) d q при д q >  0 ,

где q – объемная доля мартенсита [7]; символ s обозначает девиатор тензора напряжений; c ₀, a ₀ - константы материала, определяемые экспериментально, дs r и дг * - изменения собственной деформации в данной точке рассматриваемой области, вызванные изменением объёмной доли мартенсита д q .

Найдем напряжения, вызванные поверхностным давлением до начала охлаждения ( q = 0), что представляет собой решение задачи Ляме при

^О r = p

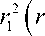
- r2

r

² r ₂

-

r ₁

° 9 = p

r i ² ( r 2 ⁺ r 22 )

r ²

-

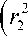
r ₁

Компоненты девиатора тензора напряжений также удовлетворяют уравнению равновесия (1) и имеют вид ri (r- 3 r2)           ri ( r+ 3 r2)

• ^sr = p^TM--A , ^{S 8} = p ^Tn-- A •

3 r ( r 2 - r i )            3 r ( r 2 - r i )

Для дальнейшего решения задачи о фазовом переходе необходимо интегрировать соотношения (5) по параметру q. Это представляет собой весьма сложную проблему, так как возникающая фазовая деформация влияет, вообще говоря, на напряжения и уравнения (1)–(5) становятся связанными. Но если фазовая деформация является свободной от напряжений, т.е. не изменяет напряжений в цилиндре, то соотношения (5) можно интегрировать по q, считая напряжения постоянными.

Проверим условия для собственной (фазовой) деформации, свободной от напряжений [24]. Уравнение совместности главных деформаций для рассматриваемого случая

d er _ —(ree) = 0                                  (8)

о r можно записать в приращениях компонент тензора собственной деформации по переменной q:

ae r* -^ ( r Se p ) = 0.                                (9)

o r

Для er* = ep = 0 (при q = 0) согласно (5), (7) получаем de p* = c0 sr 5q = c0 p1

r i ( ^r "

3 r ² ( r ₂ ²

- r

^d q , de ^p * = c о s ₆5 q = c о p

r 1 ² ( r ² + 3 r ₂ ² )

22  2

³ r ( ^r 2 ^- r i ) J

d q .

Подстановка соотношений (10) в (9) показывает тождественность деформаций de r и de g в рамках уравнения совместности.

Поскольку граница Г u = 0 для поставленной задачи, то выполнение необходимых условий доказывает, что собственные деформации (10) являются свободными от напряжений [24].

При следующем приращении 51 q соотношения (5) дают d1eP* = (c0sr + a0dep*) 51 q , S^p* = (c0sr + a09epph) 51 q , что также удовлетворяет условию для собственной деформации, свободной от напряжений, так как напряжения sr и sg не изменились после первого шага dq, а деформации 5ep* и Sep* после первого шага свободны от напряжений.

Следовательно, зная напряжения (6), можно найти фазовую деформацию, возникающую при мартенситном переходе, интегрируя уравнения (5):

ph ^e r

I

Se p* c ₀ s_r + a ₀ e p*

ph ^e Q = 1. 1

aep*

^c 0 s r ^{+ a} 0^e9

= 1.

Результат интегрирования:

e p* = c L( e^a 0 _ i ) s r , _£ p* = c L( e^a 0 _ i ) s _g . Л                 Л

a ₀                      a ₀

Поле перемещений, соответствующее (11), будет следующим:

u r = ^{e p} *^r = p

c , _xr ²( r ² + 3 r 2) c- ( e^a 0 — 1 ) 1 /2 2 <  ^a 0^{V 7} 3 r ( r 2 - r i )

.

Тогда искомая зависимость p ( u ₀) может быть представлена в виде соотношения

_ a 0      1      ^{3 r} ( r i2 ^- r 22 )

p = u 0 c 0 ( e 0 - 1 ) r ² (3^ + r ² ) ■

Компоненты тензора напряжений в цилиндре в зависимости от величины p определяются с помощью соотношения (6):

u a 1 ³ r ⁽ r i ^{2 -} r 2 ² ) Г 12 ( r" - r ²) 0 c 0 ( e ^{a 0} - 1 ) r ^ ( 3 r ² + r ² ) r ² ( r i ² - r 2 )

_n      Ol 1 ³ r ⁽^ r 2 ² ) r 1 ² ( r 22 + r ²)

. (13)

^{a e}"" u 0 c 0 ( e a 0 - 1 ) r ² ( 3 r ² + r ²) r ² ( r ² - rb

Постановка и решение задачи 2

По аналогии с первой частью решение второй подзадачи можно провести, рассматривая внешний цилиндр в отдельности от внутреннего. При этом действие на проток стента при его расширении необходимо заменить соответствующими граничными условиями в виде задания перемещений на внутренней границе протока.

Как было отмечено ранее, диаметр просвета стенозированного протока равен 2 R_C , внешний диаметр протока определяется толщиной его стенки, равной 1 мм. Будем полагать, что внешняя (по отношению к протоку) среда не сопротивляется растяжению протока, т.е. давление, приложенное к внешнему контуру цилиндра, равно нулю. Стент увеличивает радиус внутренней поверхности R _C на величину u 0 ( и 0 = R 0 - R C ) (рис. 5), рассмотренную на предыдущем этапе решения задачи.

Таким образом, получаем следующую постановку осесимметричной плоской задачи теории упругости.

Условия равновесия:

. C2             C2      1- V-V C21 + V оr = 2C1 +—, Ое = 2C1--, и = 2 C1—----—            (14)

r        r      E rE где о r, ое и и - радиальные, окружные напряжения и перемещения в точках цилиндра, удалённых на расстояние r от его центра; E и ν – модуль упругости и коэффициент Пуассона материала. Постоянные C1 и C2 определяются из граничных условий и (r = Rc) = и о, о r (r = R1) = 0 , где RC – начальный радиус стенозированного протока; R1 – внешний радиус протока. Подставляя данные условия в соотношения (3), получаем о r

R С u 0 E               R С R 1² u 0 E      1

R C (1 -v ) + R 1² (1 -v ) R C (1 -v ) + R 1² (1 -v ) r ² ’

R_c и ₀ E              R_c R ₁ ² и ₀ E      1

R C (1 -v ) + R 1² (1 -v ) ⁺ R C (1 -v ) + R 1² (1 -v ) r² ’

Рис. 5. Схема подзадачи 2

u =

R _c u 0 E      1 -v         R _c R i u 0 E     1 + v 1

---7-----------------7--r +-- 7-----------------7---7" .

R C (1 -v ) + R ²(1 -v ) E    R C (1 -v ) + R ²(1 -v ) E r ²

Результаты

Результаты решения задачи 1

В работе [19] представлено решение задачи оптимизации для нахождения оптимальной формы протока при рубцовом стенозе с учётом индивидуальных особенностей пациента. В данном случае примем диаметр протока равным 8 мм, соответствующим значению в норме, т.е. r1 = R ₀ = 0,004 м. Материалом, из которого изготовлен стент, является никелид титана ( c ₀ = 2 - 10 - 5 1/МПа, а₀ = 0,172 [7]). Таким образом, для внешнего контура рассматриваемого цилиндра (при толщине его стенки в 1 мм) зависимость (1) можно представить в виде графика, приведенного на рис. 6.

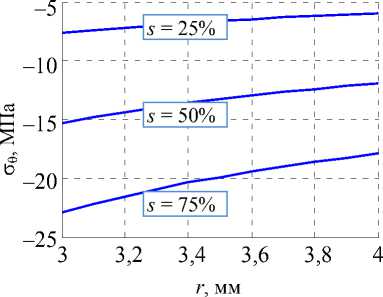
Отметим, что на представленном графике степень стенозирования s протока (отношение RC к R 0 ) варьируется от 0 до 75%.

Для разной степени стенозирования s графики напряжений (2) в зависимости от радиальной координаты изображены на рис. 7.

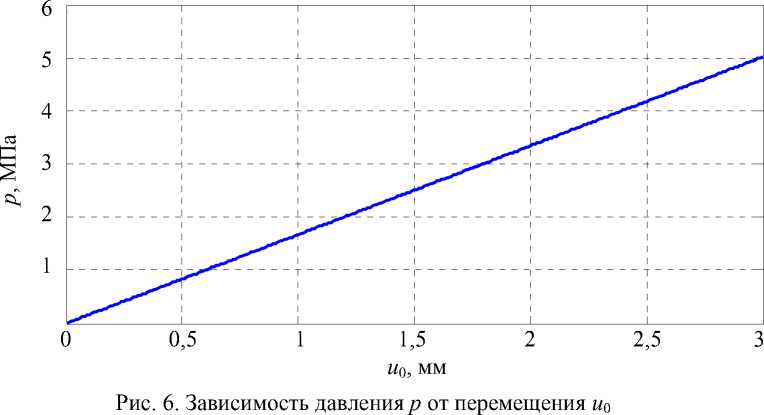
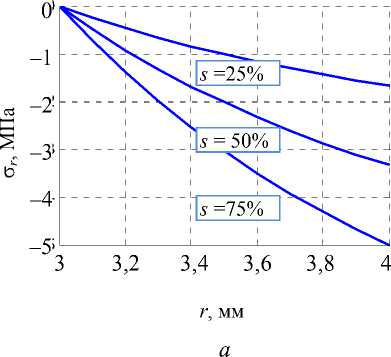
Рис. 7. Распределения напряжений в стенте при различной степени стенозирования: а – радиальные напряжения, б – окружные

б

Согласно этим графикам напряжения, возникающие в модели стента даже при его значительном сжатии, далеки от критических значений (предел прочности никелида титана составляет 1100 МПа [9]).

Результаты решения задачи 2

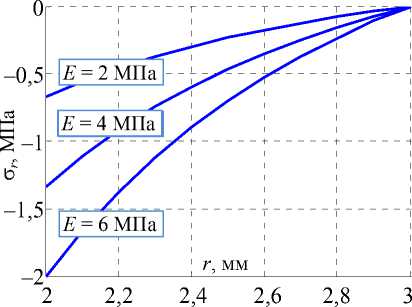
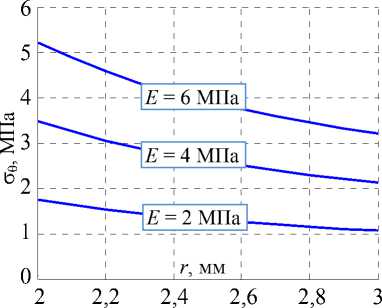
При различных значениях модуля упругости E протока и коэффициента Пуассона v = 0.4 (величины E и v взяты из работы [21]) напряжения, выраженные в формулах (4), (5) определяются графиками, приведенными на рис. 8 ( s = 50%, т.е. R _c = 2 мм, R 0 = 4 мм).

а

б

Рис. 8. Распределения напряжений в желчном протоке при различной степени стенозирования: а – радиальные напряжения, б – окружные

а                                             б

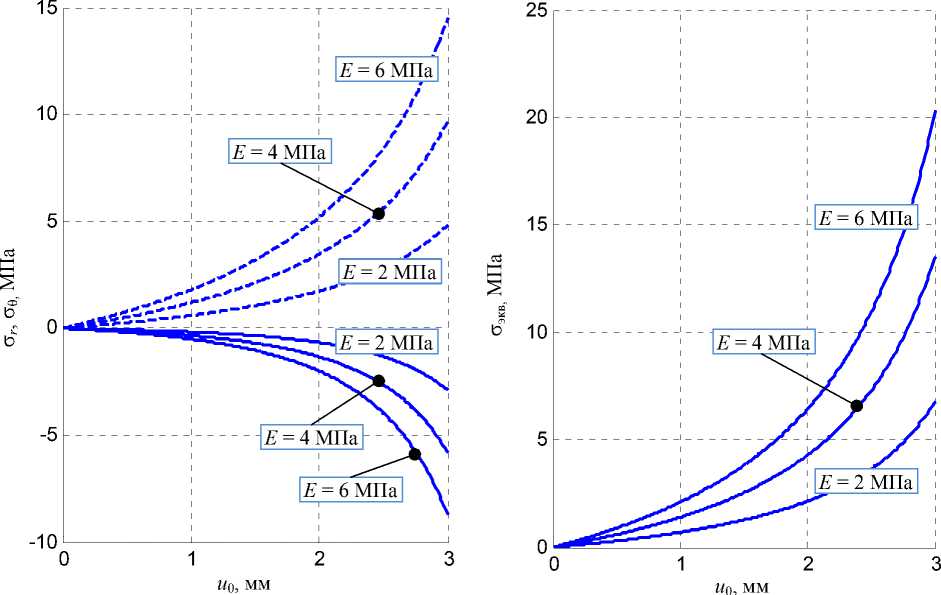
Рис. 9. Зависимости напряжений от u 0 при различных модулях Юнга желчного протока: а - радиальные о r ( и о ) (сплошная линия) и окружные напряжения о д ( и о ) -пунктирная линия; б - эквивалентные напряжения о _экв( и ₀)

Из графиков видно, что наибольшие напряжения реализуются на внутренней границе модели протока. Поэтому целесообразно рассмотреть компоненты σ _r и σ_θ в данной области в зависимости от величины u 0 . На рис. 9 изображены графики функций σ _r ( u ₀) и σ_θ ( u ₀) при r = R _C , а также соответствующие эквивалентные по Мизесу напряжения σ _экв .

Согласно литературным данным, эквивалентные напряжения в протоке не могут превышать величины, равной 4,42 МПа [23]. Исходя из этого, можно сделать вывод о том, что при условии принятых допущений и данных разрушения тканей протока будут наблюдаться при значениях переменной u 0 выше 1,6; 2 и 2,6 мм для величин модуля упругости 2; 3 и 6 МПа соответственно.

Заключение

В представленной работе на основе простейшей модели самораскрывающегося стента из материала с эффектом памяти формы показан подход к решению задачи о стентировании большого дуоденального сосочка. Данный подход позволяет оценить напряженно-деформированное состояние модели системы «стент – проток» при ее расширении, что делает возможным проведение анализа возникновения разрушений биологических тканей. Например, согласно приведенным вычислениям, при оптимальном диаметре просвета протока радиус стенозированного протока R C не должен быть меньше 2,4 мм, если модуль его упругости равен 2 МПа.

Таким образом, развитие описанной модели позволит реализовать объективную систему помощи для принятия решений по установке стентов при стенозах терминального отдела гепатикохоледоха различной этиологии.

Благодарности

Данная работа выполнена при поддержке гранта РФФИ 16-08-00718 и гранта «Государственное задание 2017–2019», шифр проекта 19.7286.2017/8.9.