Математическое моделирование многопараметрового контроля с учетом конструктивных особенностей вихретоковых преобразователей
Бесплатный доступ
Рассматриваются вопросы математического моделирования при многопараметровом контроле. Цель работы - обоснование необходимости учета конструктивной особенности датчика при построении математических моделей многопараметрового контроля и разработка методологии определения обобщающей характеристики - коэффициента конструктивной чувствительности вихретокового преобразователя. Методология определения основана на анализе годографов вихретокового контроля. Произведены вычислительные эксперименты для расчета конструктивной чувствительности для каждой измерительной точки и всех толщин образцов и величин зазоров. Результаты позволяют оценить конструктивную эффективность используемого вихретокового датчика.
Вихретоковый контроль, конструктивная особенностьдатчика, конструктивная чувствительность вихретокого преобразователя
Короткий адрес: https://sciup.org/147232834
IDR: 147232834 | УДК: 53.087 | DOI: 10.14529/mmph190409
Текст научной статьи Математическое моделирование многопараметрового контроля с учетом конструктивных особенностей вихретоковых преобразователей
Введение. В условиях эксплуатации на протяжении длительного времени трубопроводы подвергаются различным внешним и внутренним воздействиям, в результате чего происходит деградация материала, коррозионные повреждения, возникают и развиваются трещины усталости на поверхностях труб и другие виды дефектов. Кроме того, возможны внутренние дефекты технологического происхождения. Несмотря на то, что проектирование трубопроводов по современным меркам и технология изготовления и монтажа должно обеспечить реализацию назначенного ресурса, исключить возможность возникновения таких дефектов нельзя. Чтобы избежать серьезных последствий влияния дефектов, вплоть до нарушений сплошности конструкций, ведущих к аварийным ситуациям, проводятся теоретические исследования работы конструкций, содержащих дефекты, моделирование критических состояний труб и вычислительные эксперименты [1–12].
Современные методы и средства неразрушающего контроля [13, 14], используемые для диагностики трубопроводов, получили широкое развитие и распространение. Одним из широко используемых методов неразрушающего контроля является метод вихревых токов.
Основными сферами использования вихретокового измерительного преобразования являются структуроскопия, дефектоскопия, толщинометрия, измерение угловых и линейных геометрических параметров, селективное обнаружение металлических предметов, измерение электрических и магнитных характеристик материалов и изделий, измерение механических напряжений и деформаций и т. д. [15]. Наряду с указанными выше достоинствами очевидно, что для получения информации об объекте при большом числе влияющих параметров требуется и большое число измеряемых параметров сигнала вихретокового преобразователя, связанных независимыми функциями преобразования с измеряемыми параметрами объекта [16]. Принципы обработки сигналов вихретокового преобразователя при многопараметровом контроле сводятся к решению системы нелинейных уравнений [17]. При составлении данных уравнений не учитывается конструктивная особенность используемого датчика. Построение математической модели ориентировано на модельный вариант: датчик, представляющий собой одновитковую катушку, расположенный непосредственно на плоскости объекта контроля.
Цель работы – обоснование необходимости учета конструктивной особенности датчика при построении математических моделей многопараметрового контроля и разработка методологии определения обобщающей характеристики – коэффициента конструктивной чувствительности вихретокового преобразователя.
Обозначения и допущения. В работах российских и зарубежных авторов рассматриваются различные подходы и разные параметры для оценки эффективности вихретокового преобразователя [18].
В работе [19] предлагается использовать параметр ξ , равный внесённой объектом контроля относительной индуктивности или относительному реактивному сопротивлению при значении обобщенного параметра β → ∞ (на большой рабочей частоте ВТП). При проведении измерений достижение больших значений β проблематично, в связи с чем значение ξ не точно отображает эффективность вихретокового преобразователя.
Введем обозначение для обобщенной характеристики вихретокового преобразователя – конструктивной чувствительности Sc .
Приведенная теория параметрического накладного датчика с магнитопроводом рассматривает понятие коэффициента взаимной индукции между катушкой и ее зеркальным отображением и представлено формулой:
3 h
M = M 0 e R э . (1)
Формула отображает взаимосвязь – экспоненциальную зависимость выходного сигнала от зазора и эквивалентного радиуса обмотки измерительной катушки. Зазор представляет совокупность реального зазора между ВТП и объектом контроля и расстояния между витками и рабочей поверхностью датчика.
Рассмотрим поведение годографов на примере решения задачи толщинометрии электропроводящего покрытия (Pb) на ферромагнитном основании (сталь 12Х18НТ). Годографы приведены на рис. 1.
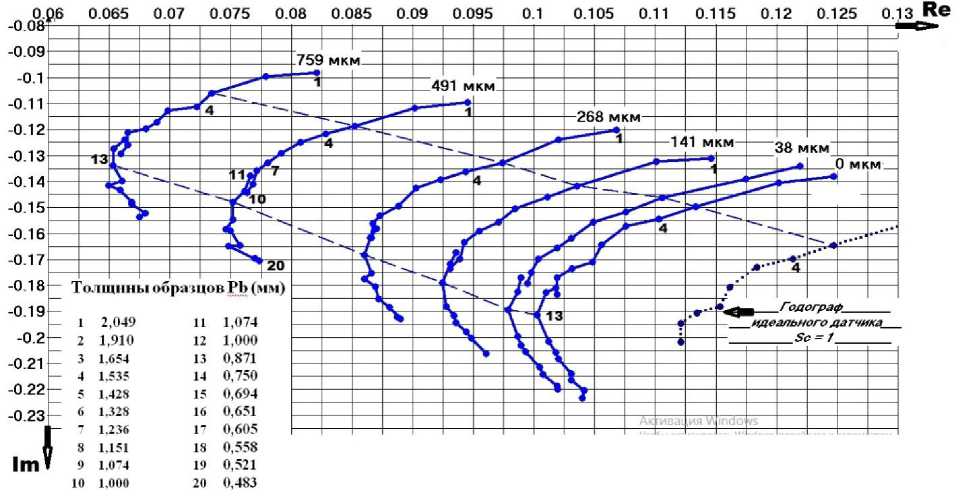
Рис. 1. Годографы обобщенных составляющих Re и Im при различных толщинах покрытия (0,483–2,049 мм) и различных зазорах (0, 38, 141, 268, 491, 759 мкм)
Измерения для построения годографов проводились в два этапа: на диапазоне измерения толщины 0,5–1,0 и 1,0–2,0 мм и с разными зазорами. Необходимость двух этапов обусловлена ограниченностью поверхности основания для размещения 20 образцов.
Эквивалентные точки по толщине покрытия для годографов с различными зазорами, соединённые между собой образуют квазилинию, уходящую в точку с координатами, близкими к 0;0 (по Re и Im составляющим).
Пусть существует годограф, который является идеальным и подобен построенным на основе измерения годографам.
Предложение 1. Предположим, что отношение длины вектора любой точки годографа с 0 зазором к длине соответствующей точки идеального годографа равно 0,90909. Обозначим данное соотношение как конструктивную чувствительность вихретокового преобразователя и представим в виде:
S c = l 0 I l ид . (2)
Тогда все годографы, расположенные левее идеального, имеют параметр конструктивной чувствительности вихретокового преобразователя меньше указанного выше нулевого годографа.
Вычислительные эксперименты . Рассчитаем значение конструктивной чувствительности для каждой измерительной точки и всех толщин образцов и величин зазоров.
Проведем расчет координат Re, Im и длину вектора для предполагаемого идеального годографа с использованием предполагаемого коэффициента 0,90909. Результаты приведены в табл. 1.
Таблица 1
Расчет координат и длин векторов
|
0,5 - 1,0 мм 0,11200 -0,19912 |
l 0,22846 |
1,0 - 2,0 мм l 0,13714 -0,15181 |
0,20458 |
|
0,11108 -0,20085 |
0,22952 |
0,13220 -0,15448 |
0,20332 |
|
0,11029 -0,21038 |
0,23754 |
0,12468 -0,16466 |
0,20654 |
|
0,11134 -0,22169 |
0,24808 |
0,12132 -0,16985 |
0,20873 |
|
0,11200 -0,22642 |
0,25261 |
0,11836 -0,17297 |
0,20959 |
|
0,11220 -0,22918 |
0,25516 |
0,11612 -0,18077 |
0,21486 |
|
0,11338 -0,23526 |
0,26116 |
0,11533 -0,18809 |
0,22064 |
|
0,11338 -0,23796 |
0,26359 |
0,11342 -0,19074 |
0,22192 |
|
0,11457 -0,24236 |
0,26807 |
0,11210 -0,19460 |
0,22458 |
|
0,11437 -0,24563 |
0,27095 |
0,11210 -0,20170 |
0,23076 |
Подобным образом рассчитываем длины векторов для всех толщин для годографов с зазорами.
Для каждого зазора рассчитаем S c согласно вышеприведенной формуле. Результаты сведены в табл. 2.
Таблица 2
Конструктивная чувствительность для каждого зазора при разных толщинах
|
0,88743 |
0,88561 |
0,83868 |
0,85071 |
0,79054 |
0,78565 |
0,69058 |
0,70690 |
0,61492 |
0,62542 |
|
0,90333 |
0,89526 |
0,85107 |
0,84628 |
0,79908 |
0,78954 |
0,70883 |
0,70657 |
0,62343 |
0,62144 |
|
0,89721 |
0,88788 |
0,84840 |
0,84957 |
0,79614 |
0,79740 |
0,69894 |
0,70730 |
0,62696 |
0,62470 |
|
0,89782 |
0,89044 |
0,84601 |
0,85065 |
0,78770 |
0,79440 |
0,69349 |
0,70540 |
0,62315 |
0,63500 |
|
0,89435 |
0,89594 |
0,84399 |
0,85767 |
0,78044 |
0,79722 |
0,69307 |
0,70986 |
0,61639 |
0,63300 |
|
0,89438 |
0,89297 |
0,84488 |
0,85367 |
0,78530 |
0,78551 |
0,68858 |
0,70476 |
0,61792 |
0,63291 |
|
0,89662 |
0,88149 |
0,83951 |
0,84102 |
0,78398 |
0,78791 |
0,69393 |
0,69876 |
0,62196 |
0,62360 |
|
0,89770 |
0,88921 |
0,84068 |
0,84947 |
0,78884 |
0,79429 |
0,68659 |
0,70434 |
0,61857 |
0,62315 |
|
0,90012 |
0,89710 |
0,84907 |
0,86389 |
0,79210 |
0,79525 |
0,69880 |
0,71495 |
0,62196 |
0,63414 |
|
0,89495 |
0,88861 |
0,83955 |
0,85312 |
0,78117 |
0,79451 |
0,68696 |
0,70731 |
0,61975 |
0,62970 |
Вычислим относительное отклонение от среднего. Результаты приведены в табл. 3.
Таблица 3
Относительное отклонение от среднего
|
0,01000 |
0,00544 |
0,00653 |
0,00105 |
0,00255 |
0,00823 |
0,00490 |
0,00039 |
0,00899 |
0,00459 |
|
0,00774 |
0,00540 |
0,00815 |
0,00626 |
0,01338 |
0,00332 |
0,02140 |
0,00007 |
0,00472 |
0,01093 |
|
0,00091 |
0,00288 |
0,00499 |
0,00239 |
0,00966 |
0,00660 |
0,00715 |
0,00096 |
0,01040 |
0,00575 |
|
0,00159 |
0,00002 |
0,00216 |
0,00113 |
0,00105 |
0,00281 |
0,00070 |
0,00172 |
0,00428 |
0,01064 |
|
0,00227 |
0,00617 |
0,00023 |
0,00712 |
0,01026 |
0,00638 |
0,00132 |
0,00458 |
0,00662 |
0,00746 |
|
0,00224 |
0,00282 |
0,00082 |
0,00242 |
0,00410 |
0,00841 |
0,00778 |
0,00263 |
0,00415 |
0,00732 |
|
0,00025 |
0,01006 |
0,00554 |
0,01243 |
0,00577 |
0,00537 |
0,00007 |
0,01112 |
0,00235 |
0,00750 |
|
0,00146 |
0,00140 |
0,00416 |
0,00251 |
0,00039 |
0,00268 |
0,01066 |
0,00322 |
0,00310 |
0,00821 |
|
0,00417 |
0,00746 |
0,00578 |
0,01442 |
0,00452 |
0,00389 |
0,00695 |
0,01180 |
0,00235 |
0,00927 |
|
0,00160 |
0,00206 |
0,00549 |
0,00177 |
0,00933 |
0,00295 |
0,01011 |
0,00098 |
0,00121 |
0,00222 |
В результате анализа получаем из 120 измерительных точек (20 образцов, 6 зазоров) 13 точек – погрешность примерно 1 %, 1 точка = 2,14 %. Полученные погрешности определения S c обусловлены наличием инструментальной погрешности при проведении измерений.
Основные результаты . Выполненные расчеты показывают, что методология определения S c инвариантна к измерительной точке.
Предложение 2. В рассмотренном вычислительном эксперименте идеальный годограф выбран произвольно. Проведя итерационные вычисления при изменении значений S c и эквивалентного радиуса вихретокого преобразователя возможно получить экспоненту совпадающей с идеальной.
Вычислительные эксперименты. Вычисления проведены с помощью среды визуальнографического программирования LabView. На рис. 2 показан модуль расчета требуемой компоненты.
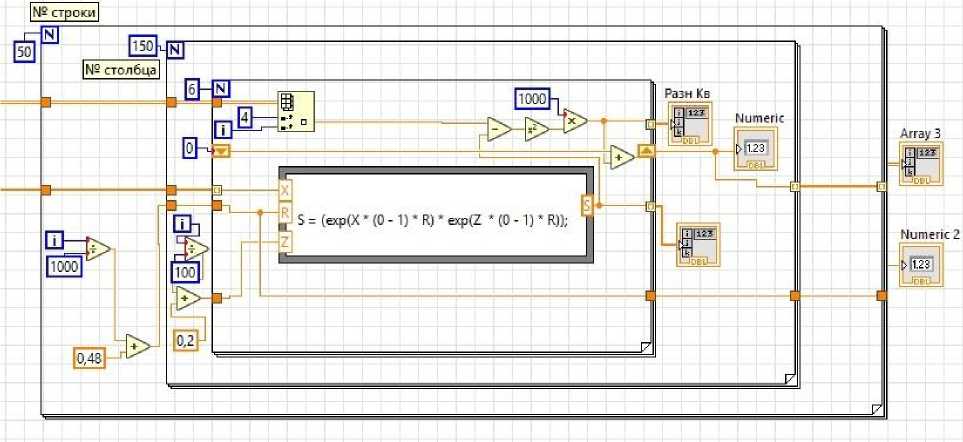
Рис. 2. Модуль расчета требуемой компоненты
В результате вычислений (табл. 4) для трех рабочих частот и трех диапазонов толщин полученные коэффициенты S c лежат в пределах от 0,69 до 0,75.
Такой разброс обусловлен наличием инструментальной погрешности в измерениях и соответственно большим разбросом определения параметров R экв . Полученная точность определения Sc вполне удовлетворяет запросам практического использования.
Таблица 4
Полученные коэффициенты S c
|
0,5-1,0 мм |
1,0-2,0 мм |
2,0- 4,0 мм |
0,75 |
|||||
|
Sc |
Вэкв |
Sc |
Вэкв |
Sc Dskb |
0,70 |
|||
|
ф s 5 H F © © H l© © « « Ph Г |
1,88 кГц |
0,75 |
15,20 |
0,71 |
11,50 |
0,70 11,50 |
0,70 |
|
|
4,2 кГц |
0,70 |
11,50 |
0,71 |
12,10 |
0,68 10,60 |
0,71 |
||
|
8,8 кГц |
0,70 |
11,50 |
0,69 |
11,10 |
0,69 11,10 |
0,71 |
||
|
0,69 |
||||||||
|
0,70 |
||||||||
|
0,68 |
||||||||
|
0,69 |
||||||||
|
Среднее |
0,70 |
|||||||
Заключение. В результате работы обоснована необходимость учета конструктивной особенности датчика при построении математических моделей многопараметрового контроля и разработана методология определения обобщающей характеристики – коэффициента конструктивной чувствительности вихретокового преобразователя. Произведены вычислительные эксперименты
Вебер В.А.
для расчета конструктивной чувствительности для каждой измерительной точки и всех толщин образцов и величин зазоров. Создана программа в среде визуально графического программирования – LabView для итерационного вычисления при изменении значений Sc и эквивалентного радиуса вихретокого преобразователя.
Список литературы Математическое моделирование многопараметрового контроля с учетом конструктивных особенностей вихретоковых преобразователей
- Дильман, В.Л. Напряженное состояние и прочность неоднородной пластической полосы с дефектом в более прочной части / В.Л. Дильман // Известия Российской академии наук. Механика твердого тела. - 2010. - № 2. - С. 89-102.
- Когут, Н.С. Несущая способность сварных соединений / Н.С. Когут, М.В. Шахматов, В.В. Ерофеев. - Львов: Свит, 1991. - 182 с.
- Dil'man, V.L. Strength of Mechanically Heterogeneous Welded Joints With a Slit-Like Defect / V.L. Dil'man, A.A. Ostsemin // Welding International. - 1999. - Vol. 13, no. 8. - P. 648-650..
- Dil'man, V.L. Load-Carrying Capacity of Straight-Seam Large Diameter Pipes with Defects at the Fusion Boundary of the Welded Joint / V.L. Dil'man, A.A. Ostsemin // Welding International. - 2003. - Vol. 17, Iss. 5. - P. 376-380.
- Dil'man, V.L. Static Strength of a Welded Joint with Hard Interlayers and Defect at the Fusion Line of the Weld / V.L. Dil'man, A.A. Ostsemin // Welding International. - 2004. - Vol. 18, no. 10. - P. 805-808.
- Dil'man, V.L. Effects of surface defects on the static strength of welds in spiral-seam tubes / V.L. Dil'man, A.A Ostsemin // Chemical and Petroleum Engineering. - 2004. - Vol. 40, Iss. 1-2. - P. 87-93.
- Dil'man, V.L. Analysis of the Ductile Strength of Welds Weakened by Notches in Longitudinally Welded Pipes of Large Diameter by the Method of Slip Lines / V.L. Dil'man, A.A Ostsemin // Strength of Materials. - 2004. - Vol. 36, Iss. 3. - P. 274-281.
- Dil'man, V.L. Static Strength of Mechanically Nonuniform Welded Joints with a One-Sided Surface Defect Subject to Ductile Failure / V.L. Dil'man, A.A. Ostsemin // Chemical and Petroleum Engineering. - 2005. - Vol. 41, Iss. 9-10. - P. 522-529.
- Dil'man, V.L. Effect of Defects on the Load Carrying Capacity of Pipes of Transmission Oil and Gas Pipelines under Biaxial Loading / V.L. Dil'man, A.A. Ostsemin // Welding International. - 2006. - Vol. 20, no. 1. - P. 63-67.
- Остсемин, А.А. Влияние дефектов сварки, расположенных на границе сплавления, на прочность сварного соединения / А.А. Остсемин, В.Л. Дильман // Вестник машиностроения. - 2006. - № 2. - С. 21-26.
- Дильман, В.Л. Математическое моделирование критических состояний мягких прослоек в неоднородных соединениях / В.Л. Дильман, Т.В. Ерошкина. - Челябинск: Издательский центр ЮУрГУ, 2011. - 275 с.
- Носачева, А.И. Математическое моделирование напряженного состояния неоднородной полосы с наружным макродефектом / А.И. Носачева // Вестник ЮУрГУ. Серия "Математическое моделирование и программирование". - 2013. - Т. 6, № 3. - С. 79-84.
- Петинов, С.В. Обзор методов дефектоскопии при обследовании трубопроводов / С.В. Петинов, В.Г. Сидоренко // Молодой ученый. - 2016. - № 2. - С. 194-199. https://moluch.ru/archive/106/25262
- Внутренние и международные стандарты методов неразрушающего контроля обсадных колонн / XU Jin-long, CAO Biao, HONG Wu-xing, LU Shan-sheng, FENG Jun-han, HUA Bin, YANG Shu-jie // Методы неразрушающего контроля. - 2014. - Т. 36, № 10. - С. 72-77.
- Ян, Ч. Физическое и математическое моделирование измерительных преобразования в полях вихревых токов / Ч. Ян // Вестник науки Сибири. - 2013. - № 3. - С. 75-85.
- Гольдштейн, А.Е. Физические основы получения информации: учебник / А.Е. Гольдштейн. - Томск: Изд-во Томского политехнического университета, 2010. - 291 с.
- Veber, V. Ongoing Control of Technological Processes for Thickness Measurement Tasks Using Eddy-Current Testing Technique / V. Veber, V. Dilman, A. Veber // 2018 International Russian Automation Conference (RusAutoCon). https://ieeexplore.ieee.org/abstract/document/8501607
- Capobianco, T.E. Eddy Current Probe Sensitivity as a Function of Coil Constuction Parametrs / T.E. Capobianco, J.D. Splett, H.K. Iyer // Reseach in Nondestructive Evaluation. - 1990. - Vol. 2. - Iss. 3. - P. 169-186.
- Учанин, В.Н. Инвариантная оценка эффективности вихретоковых обмоток для разработки новых преобразователей и технологий контроля / В.Н. Учанин // Материалы 7-й национальной конференции "Неразрушающий контроль и техническая диагностика UkrNTD-2012". - Киев: УТ НКТД, 2012. - C. 66-71.


