Математическое моделирование молодежной субкультуры

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 51-77                                          

В изобразительном искусстве Японии в XX веке зародилось художественное течение рисунков в виде комиксов, из которого постепенно за счет техники исполнения возникло течение «манга» [1]. Затем мангу начали экранизировать в виде анимационных фильмов – аниме. Сегодняшние информационные технологии сделали доступным аниме для широкой аудитории. Из изначально развлекательного характера искусство манга - аниме стало восприниматься как самостоятельная молодежная субкультура со своими жанрами и направлениями. В целом в субкультуру поклонников аниме включаются и такие направления как ранобэ, маньхуа и другие версии мультипликации и комиксов, создаваемые в большинстве в восточных странах (Китай, Корея, Филиппины) [2].

Субкультура поклонников аниме, манга, мультфильмов и комиксов основывается на современных информационных технологиях передачи и получения данных. Часть материалов передается на традиционных носителях, однако основным источником являются интернет-ресурсы.

Статистические данные

Авторы использовались данные собственного социологического исследования. Результаты опроса сопоставлялись с данными аналогичного опроса, проведенного в [3] и материалами, приведенными на сайте GoogleTrends, который является публичным измерительным устройством поисковика корпорации Google.

По результатам опроса была определена возрастная структура респондентов: 80% респондентов имели возраст от 14 до 30 лет включительно. Средний возраст опрошенных составлял 22 года, верхняя возрастная граница — 60 лет, а нижняя — 9 лет. 85% респондентов имели высшее или неоконченное высшее образование, оконченное или неоконченное среднее профессиональное образование. То есть возрастная структура, высокий уровень образования большинства респондентов говорят об осознанном понимании сюжетов тайтлов и уровня их исполнения в технике мультипликации. Полученные данные согласуются с данными, приведенными в «Возрастные предпочтения в выборе аниме как объекта сетевой коммуникации» и Anime Recommendation engine: From Matrix Factorization to Learning-to-rank .

Вопросы, связанные в деструктивными процессами в субкультуре [4], внешним влиянием на поклонников не рассматривались [5].

Динамика запросов российских поклонников по наименованиям: мультфильмы, аниме, манга, комиксы была получена с помощью сервиса Google Trends. Учитывались запросы по наиболее популярным 20 произведениям. По России были учтены 4100 запросов по мультфильмам, 1350 — по комиксам, 10600 — по аниме, 9940 — по манга в период с 2004 по 2023 год. На Рисунке 1 приведены годовые относительные распределения запросов по манго и аниме, комиксам и мультфильмам. Как следует из анализа статистических данных, количество запросов по мультфильмам росло с 2004 г. по 2014 г., а с 2014 г. стало уменьшаться. Для случая комиксов уменьшение числа запросов с 2006 г. по 2010 г. сменилось на увеличение до 2015 г. с последующим уменьшением. Запросы на манга и аниме росли практически одинаковыми темпами.

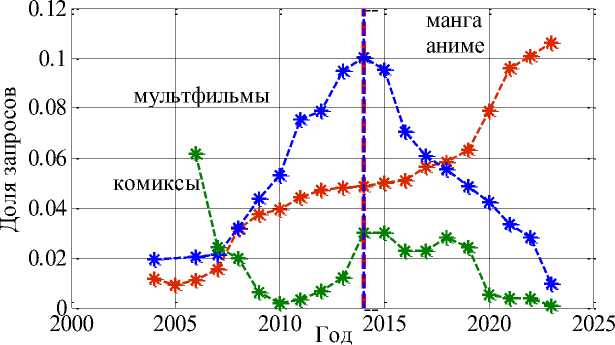
Рисунок 1. Распределение запросов по годам

На Рисунке 2 приведены кумулятивные зависимости для аниме, манга, мультфильмов и комиксов по всем произведениям с 2004 г. по 2022 г. Как следует из анализа этих данных общий интерес к аниме и манга растет, начиная с 2004 г., в отличие от мультфильмов и комиксов. Статистические данные по направлениям отмечены символом «*». Данные за 2004 г. принятых равными 1. Как следует из анализа данных, приведенных на Рисунке 2, интерес к манга и аниме растет одинаковыми темпами.

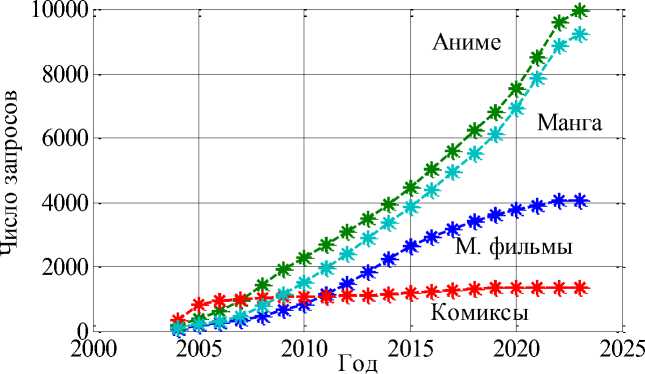
Рисунок 2. Динамика числа запросов (кумулятивные зависимости)

Анализ статистических данных показывает, что интерес к аниме, манга, комиксам и другим видам современным познавательно-развлекательным направлениям проявляет большая группа лиц. Они имеют контакты между собой, привлекают в свое сообщество новых членов. Интерес к конкретным направлениям может угасать, а к некоторым увеличиваться. После некоторого насыщения интерес может изменяться — одни участники покидают субкультуру, а на смену им приходят новые. В целом поклонники аниме, манга и близким к ним направлениям образуют молодежную аниме-субкультуру.

Основная масса участников субкультуры аниме имеет возраст от 9 до 30 лет. То есть интерес к аниме угасает к 30 годам, но на место покинувших поклонников приходят лица младшего возраста. На временном интервале в 10–15 лет численность всего населения страны изменяется незначительно. С учетом этого можно принять, что численность субкультуры аниме может изменяться за счет угасания интереса к аниме, или проявления интереса к другим направлениям, или за счет прихода новых участников других жанров, или прихода новых поклонников из младших возрастных групп. Поскольку численность населения РФ в возрасте от 10 до 30 лет ограниченная величина, составляющая около 30% от всего населения РФ, то и количество поклонников субкультуры не может превышать некоторого максимального значения.

Рост познакомившихся с одним из направлений субкультуры впервые и вовлеченные в субкультуру, как следует из анализа статистических данных, растет по экспоненциальной зависимости. В то же время и динамика запросов на просмотр аниме, комиксов и других направлений также растет по экспоненциальной зависимости. Однако годовое число запросов по одним направлениям, достигнув максимума, начинает убывать. Это можно рассматривать как изменение интереса участников к конкретному направлению. Аналогичный вывод следует и из кумулятивных анализа зависимостей (Рисунок 2).

Математическая модель молодежной субкультуры

В возрастной структуре населения группа молодежи в возрасте от 10 до 25 лет составляет около 20% от всего населения страны или региона. Этот показатель не изменяется на длительном временном интервале. Лица, превысившие этот возраст, постепенно покидают группу молодежи, а лица, достигшие нижнюю границу, попадают в эту группу. С учетом этого численность молодежи в этой группе можно считать само регулируемой величиной около некоторого порогового значения. У части молодежи этой группы возникает интерес к конкретным ценностям. За счет межличностных контактов или каких-то иных информационных источников они становятся поклонниками конкретной субкультуры. Поскольку интересы к каким-то общим ценностям у поклонников несколько отличаются, то возникает субкультура, наполненная различными ценностями близкими по содержанию к определяющим. Численность поклонников субкультуры, как и в случае обшей группы молодежи, также будет само регулируемой величиной. В отличие от стабильной численности основной группы численность участников субкультуры может увеличиваться за счет появления новых ценностей, или уменьшаться вплоть до полного распада в случае исчезновения интереса к конкретным ценностям.

Модель формирования нескольких направлений в субкультуре основывается на камерной модели метастазирования новообразования [6]. В математической модели динамики молодежной субкультуры предполагается, что субкультура может образовываться на нескольких близких по содержанию направлениях. Возникшая группа поклонников одного из первых доступных для освоения направлений постепенно увеличивается в численности. Со временем из этой группы часть поклонников начинает осваивать следующее направление. При этом численность поклонников освоенного направления начинает уменьшаться. Предполагается также, что численность группы потенциальных поклонников субкультуры является само регулируемой величиной. Такой поход позволяет учесть постоянный приток новых потенциальных поклонников.

Численность потенциальных участников молодежной субкультуры само регулируемая величина. Динамику ее численности N(t) можно описать логистическим уравнением [7, 8]:

tfM1-?)- dt      УК/

где / — удельная скорость роста численности группы потенциальных поклонников при малой ее численности, К — максимальная возможная ее численность.

Пусть в молодежной субкультуре одновременно существует М направлений, к которым проявляется интерес. В каждом направлении есть N i ( i = 1, 2, ..., М ) участников. Участники группы i по мере угасания интереса к этому направлению со скоростью faNN t переходят в i + 1 -ю группу заинтересованных лиц. По мере уменьшения интереса P i N i участников i -ой группы покидают свою группу и переходят в i + 2-ю группу, и так далее модель формирования М групп

М, молодежной субкультуры, К — скорость роста ее численности.

вплоть до группы М . С учетом этих предположений (освоения направлений) имеет вид

M dN

= —N) ^jNi+^N(1 — N/K), dt i=1

dN

• ¹    = ^₁NN₁ — P₁N₁, dt

dN

• -= = V i NN — P i N i + P i-1 N i-1 ,  i = 2,

dt

. . .,

где N — численность потенциальных поклонников максимально возможная ее численность, ^ — удельная

Параметры V i и P i характеризуют скорости пополнения и убыли участников групп.

Суммарная численность участников всех направлений подсчитывается по формуле u(t)=^₌ i Ni(t).

Таким образом, модель (2) учитывает, что увеличение численности группы i происходит за счет новичков, пришедших в субкультуру (слагаемые ^ j NN j ), и за счет перехода в нее части участников группы i — 1 (слагаемое P_l-}N_l-} ). Число потенциальных поклонников субкультуры учитывается с учетом модели (1) увеличения ее численности.

К системе уравнений (2) добавляются начальные условия

N = N ⁰ ,N_i = N ⁰ (i = 1,...,М)

Начальные условия подразумевают, что в начальный момент времени могут быть увлеченные любым направлением. К ним можно отнести и основателей материальной основы направления.

Система уравнений (2) имеет стационарную точку, в которой

N = N 1 = N 2 =...= N_M = 0.

Эта стационарная точка будет неустойчивой, поскольку в этом случае матрица Якоби правой части уравнений (2) имеет положительное собственное значение Л = у.

В стационарной точке

N = K,N 1 = N 2 =...= N_M = 0                              (3)

собственными значениями матрицы Якоби являются

Л = —у, A_i = ^К — P_i(i = 1,2, ..., М).

Все собственные значения матрицы Якоби будут отрицательными, если выполняются неравенства

ViK < Pi для всех i = 1, 2, ..., М.

В этом случае стационарная точка (3) будет устойчивой. Поэтому в этом случае принимается, что интерес ко всем течениям угасает со временем, а сама молодежная субкультура распадается. При этом группа потенциальных поклонников численностью К не проявляет ни к чему интерес, поскольку исчезли участники все направлений.

Если для течения т выполняется неравенство ц_тК > р_т , то стационарная точка (3) будет неустойчивой. В этом случае интерес к этому течению сохраняется. Поскольку часть участников этого течения переходят в группу т + 1, то интерес буде сохраняться и к последующим направлениям.

На Рисунке 3 приведено относительное изменение функций N j = N j (t)/K (i = 2,3,4) для случая четырех направлений в субкультуре при следующих значениях параметров: К = 50 , у = 0,1, ц = (0,015, 0,014, 0,014, 0,014) , £ = (0,35, 0,50, 0,40, 0,60) . Параметры подбирались исходя из статистических данных по динамике роста численности участников четырех направлений субкультуры аниме (Рисунок 1–2). Представлен вариант нарушения условий /К < £ i , то есть неустойчивости стационарной точки (3). В этом случае, как следует из анализа полученных результатов, считается, что интерес к некоторым направлениям субкультуры со временем может уменьшаться, а потом постепенно проявиться снова (Рисунок 3).

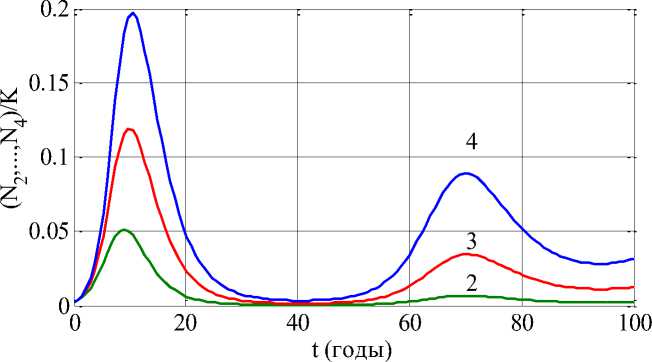
Рисунок 3. Изменение функций N j = N j (t) (i = 2,3,4) во времени

При малых начальных значениях функций N j (t) ( N j⁰ «К ) эти функции будут возрастающими функциями в начальный момент времени. Как следует из анализа системы уравнений (2) экстремум в зависимостях N j = N j (t) достигается при выполнении условий / j N = P j (i = 1,2, ..., М). Поскольку параметры / j и P j для всех направлений разные, то и времена достижения экстремума численности поклонников направлений будут отличаться (Рисунок 3). Момент достижения экстремума можно рассматривать как момент начала уменьшения числа участников соответствующего направления, или как уменьшения интереса к нему. Момент начала уменьшения интереса ко всем направлениям субкультуры можно сопоставлять с моментом достижения максимума функцией u(t) =Ejt₁N j (t), и считать началом уменьшения общей численности участников всех направлений.

Имитационное моделирование

Имитационное моделирование различных социальных систем на основе математических моделей позволяет оценить возможные эволюционные траектории, времена начала деградации социума, наличие точек бифуркации, пороговые значения управляющих параметров [7, 8].

Входящие в систему уравнений параметры щ и P i , и начальные значения функций N j⁰ (i = 1, ..., М ) для реальной субкультуры являются случайными величинами. Выбирая их случайным образом из заданного диапазона можно оценить возможные варианты динамики численности отдельных направлений и динамику общей численности субкультуры. Для случая параметров щ и в , выбранных случайным образом из диапазонов (0,005, 0,015) и (0,3,0,5), соответственно, на рис. 4 приведены распределения времен достижения максимума функцией u ( t ) (рассматривается как длительность интереса) для L = 1000 вариантов изменения параметров. Зависимость М = 4 соответствует субкультуре с четырьмя направлениями, а М = 16 — субкультуре с шестнадцатью направлениями. Как следует из анализа полученных результатов (Рисунок 4) длительность активного периода существования субкультуры тем больше, чем большее число направлений она содержит.

Численное решение задачи Коши для системы уравнений (2) и имитационное моделирование осуществлялось в среде программирования математического пакета MatLab [9].

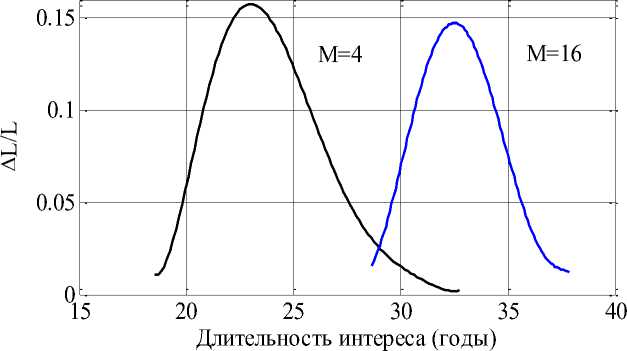
Рисунок 4. Относительное распределение времен достижения максимального значения функцией u (t).

Математическая модель (2) учитывает постоянное пополнение участников именно молодежной субкультуры и изменение интереса поклонников к различным ее направлениям. Модель позволяет также оценить и временной интервал функционирования молодежного объединения. Модель динамики молодежной субкультуры дает инструмент прогнозирования ее внутренней перестройки. Корректировка модели с использованием статистических измерений предоставляет возможность контролировать и организовывать управление молодежным объединением с принятием организационных решений с учетом социальной значимости направлений [4, 5], оказывать техническую поддержку субкультуре.

Заключение

Молодежные субкультуры с различными направлениями существуют в социуме многие годы. Со временем происходит угасание интереса поклонников к конкретным направлениям, но возможно и возрождением интереса. Модель молодежной субкультуры прогнозирует этот результат. Наиболее рациональным в социуме следует считать постоянную генерацию новых культурных направлений или обновление существующих, позволяющих развиваться молодежи. Это позволит увеличить временной интервал функционирования субкультуры, а при активном управлении формированием направлений готовить молодежь для решения задач, которые могут возникнуть в будущем.