Математическое моделирование мультиинертного колебательного механизма

Свободные гармонические колебания классического маятника обусловлены взаимным преобразованием кинетической энергии груза в потенциальную энергию пружины [1, 2]. Разработаны осцилляторы с другим характером энергообмена, например, преобразованием кинетической энергии груза в энергию магнитного поля соленоида или энергию электрического поля конденсатора. Все эти колебательные системы и подобные им [3–20] явились предпосылкой создания биинертного осциллятора, в котором ускорение одного груза происходит за счет торможения другого, т. е. происходит обмен только кинетическими энергиями.

Целью работы является математическое моделирование мультиинертного колебательного механизма.

Основными методами исследования в рамках настоящей работы являются методы математического моделирования и анализа. Использованные методы позволяют получить достоверное описание исследуемых объектов.

Синтез колебательного механизма

Пусть в плоскости Z имеются не две, а n координатных осей 0 x ₁,0 x ₂,...,0 x_n , образующих центрально симметричную звезду с центром в точке 0 . Угол между осями составляет π/ n . Из начала координат 0 отложен вектор R . Направление вектора произвольное. R ⊂ Z .

Теорема 1

• 1.    Отрезки, соединяющие координаты x ₁, x ₂,..., x_n вектора R в системе координат 0 x ₁,0 x ₂,...,0 x_n , образуют правильный n -угольник.

• 2.    Размер n -угольника не зависит от ориентации вектора R .

• 3.    Середина вектора R совмещена с центром n -угольника.

Доказательство . Вектор R имеет координаты:

X i = R cos ф ,

I П | x2 = R cos I--ф I, к n J d I2n 1 x3 = RcosI--ф I, к n J xi = R cos

( i - 1) n

n

x_n = R cos

( n - 1) n

n

В соответствии с теоремой косинусов

( ^Xi^Xi + 1 ) = ^{R 2 I c}os ²

( i - 1) я

--ф

n

,     2i i я     1 _o

+ cos I--ф I- 2 cos к n J

( i - 1) я

--ф

n

I i я     1     я I cos I--ф I cos — f = к n    J    n

^П i        i ^П                   i ^П • i .

cos—I cos—cos ф + sin—sin ф I + n к     n           n J

I 21 i ^{П П} 1 . I i ^П . • i ^П •       I

= R < cos I--ф—I+I cos — cos ф + sin—sin ф| - 2

[к n n J к n n J

. я i . i я                    i я .      1 i i я . i я . 1 я I

+ sin—I sin—cos ф- cos—sin ф I I cos—cos ф + sin—sin ф I cos— f = n к n n JJк n n J n

I 2 ^я 2 i ^я 2        2^я- 2 i ^я - 2      -2^я- 2 i ^я    2      -2^я    2 i ^я - 2

= R I cos —cos —cos ф + cos —sin —sin ф + sin —sin —cos ф + sin —cos —sin ф + к n n n n n n n n

• 2 я iя . iя .       _ я     iя     2 ■ я ■ iя          я 2 iя.

+2cos —cos—cosфsin—sinф + 2cos—cos—cos фsin—sin--2cos—cos —cosфsin—sinф + nn n nn nn n n n я . 2 iя ■ ■ я я ■ iя ■ 2 ■ я iя -2 я ■ iя

+2cos—sin —sinфsin—cosф-2cos—sin—sin фsin—cos--2sin —sin—cosфcos—sinф + nn n nn nn nn n

2 iя     2 . ■ 2 iя ■ 2 . iя ■ iя ■              2 я 2 iя2

+ cos —cos ф + sin —sin ф + 2cos — cos ф sin—sin ф- 2cos —cos —cos ф- nnnnnn

_ 2 я ■  iя  ■         iя          _ . я .  iя     2       iя     я . О ■ я 2 iя■

- 2cos —sin—sin ф cos — cos ф- 2sin—sin—cos ф cos—cos— + 2sin—cos —sin ф cos ф cos— nn n nn nn n n n

_ 2 ^я       i ^я          . i ^я .        _ 2 ^я . 2 i ^я .2

- 2cos —cos — cos ф sin—sin ф- 2cos —sin —sin ф- nn n n n

. ^я . 2 ^{i n} • ^я . • ^я i ⁿ . 2 ^{i n я} 1

-2sin—sin —cosфsinфcos— + 2sin—cos—sin фsin—cos— I = n n n n n n n J

Г 2 I ■ 2 я . 2 i n       2 я 2 i n       2 i n 1

= R I cos ф! sin —sin--cos —cos —+ cos —I +

^L к n n n n n J

I ■ 2 ^я 2 ^{i n}        2 ^я ■ 2 ^{i n} . ■ 2 ^{i n} I

+ sin фI sin —cos--cos —sin — + sin — I = к n n n n n J

— 2 Г 2 I ■ 2 я . 2 i я . 2 я 2 i П 1     . 2 I ■ 2 П 2 i П . 2 П . 2 i П 1

= R I cos фI sin —sin — + sin —cos —I + sin фI sin —cos — + sin —sin —I =

^L к n n n n J к n n n n J

= R ²

2 . 2 nI ■ 2 iП .       2 iП I . ■ 2 ■ 2 nI 2 iП . ■ 2 iП I cos фsin —I sin — + cos — I+ sin фsin —I cos — + sin n к     n        n J             n к nn

Г>21              2 я .     2    • 2я I            2 я/   _2    .     2 \    r>22

= R I cos ф sin — + sin ф sin — I = R sin —(cos ф + sin ф) = R sin —.

к n nJ n^' n

Расчет и конструирование

Из этого следует, что все стороны n -угольника одинаковы по длине. При этом их длина не является функцией ф , т. е. не зависит от ориентации вектора R .

Далее середина вектора R обозначается r . В соответствии с теоремой косинусов

7 X 2 Л   ₂Г ( i - 1 ) п    1    1         Г ( i - 1 ) п    1 1      Г ( i - 1 ) п    11    R R

( xr ) = R  = —.

I L n       J   4        L n       J 2     L n       JJ 4

Из этого следует, что все отрезки, связывающие точку r с вершинами n -угольника, имеют одинаковую длину. Это означает, что n -угольник является правильным и точка r совпадает с его центром.

Теорема доказана.

Теорема 1 позволяет определить конфигурацию мультиинертного осциллятора, упрощенная схема которого показана на рисунке.

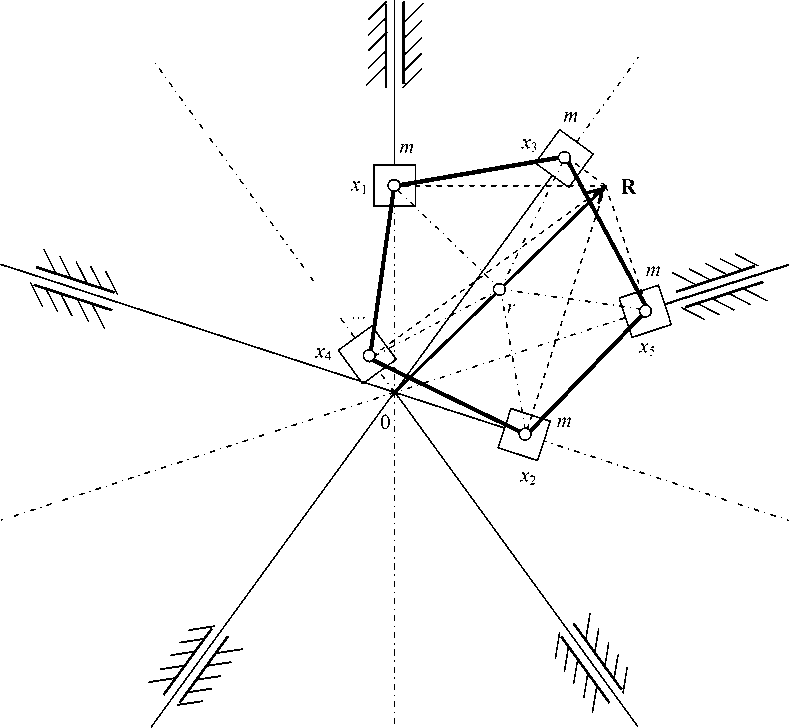
m

Мультиинертный осциллятор

Для целей теоремы 1 вершины правильного многоугольника рассматривались в одной плоскости Z . Для инженерных целей траектории грузов не должны пересекаться, поэтому грузы и их направляющие расположены в параллельных плоскостях подобно цилиндрам, шатунам и кривошипам в кривошипно-шатунном механизме. Для обеспечения этого, например, стержень x 1 x 3 закреплен «сверху» (ближе) груза, находящегося в координате x 1 , а стержень x 1 x 4 – «снизу» (см. рисунок).

Анализ колебательного механизма

Внешние силы к системе не приложены. Скорости инертных тел массой m каждое определяются как производные их координат. В соответствии с (1), (2)

dx „ .d

—1 = - R sin ф— dt dt dx-) „ . In1

—2 = R sin | —ф I—, dt V n ) dt dx-,   „ . ( 2n1

—3 = R sin I dt V n ) dt dx

—^L = R sin dt

(i - 1)n

--ф

n

d ф dt ^,

dx

—n = R sin dt

(n - 1)n ф

n

d ф dt ^.

Для того чтобы в системе происходили свободные гармонические колебания, необходимо, чтобы ее полная энергия оставалась постоянной. В данном случае полная энергия системы имеет вид:

•2      -2 ( П 1         . 2 ( i - 1) n               • 2 ( n - 1) n      || d ф |

sin ф + sin-- ф + ... + sin-- ф + ... + sin-- ф И — .

Vn                 L n J L n JJV dt)

Теорема 2

При n >  2 имеет место выражение:

n

Ё sin2

i = 1

( i - 1)n ,

---— ±ф

n

n

.

Доказательство

n

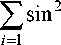
( i - 1) n n

±ф =

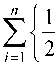
—cos

Ы^ 2 ф n

n

• 1    _o ( i - 1)2n_ 1 . _o . ( i - 1)2 n — cos 2 ф > cos -----— +—sin 2 ф >  sin -----— .

• ²          i = 1           ^{n 2}         i = 1          ⁿ

Если вдоль координатных осей 0x1,0x2,...,0xn отложить единичные векторы, то их сумма вследствие центральной симметрии будет равна нулю. Следовательно, сумма проекций этих единичных векторов на любую из осей 0x1,0x2,...,0xn также будет нулевой. По этой причине по- следние две суммы тождественно равны нулю.

Теорема доказана.

Следствие . При n = 2 выражение (4) приобретает известный вид:

I п 1-                          2sin ф + sin I 2 + ф I = sin ф + cos ф = 2 = 1.

Точно также доказывается

Теорема 3

При n >  2 имеет место выражение:

n

Ё ^cos 2

i = 1

( i - 1)п ,

---— ±ф

n

n

. 2

С учетом теоремы 2 (выражение (4)) полная (она же кинетическая) энергия (3) равна

_Т 1    nd d ф1 ²

T = —nmR I — I = const.

• 4 V dt )

Из последнего выражения следует

Расчет и конструирование

d ф

— = const.

dt ф = C1t + C2.

Начальные условия для фазы и угловой скорости:

ф(°) = Фо, d Ф/m

—⁽⁰⁾ = ® 0 .

dt

Отсюда C 2 = Ф о , C 1 = to o .

Формулы для координат грузов (1)–(2) принимают вид: x1 = R cos (toot + ф0), x 2 = R cos I n-to01 -фо I, к n )

„   Г 2 n     . )

x3 = R cos I--to01-ф0 I, к n )

x i = R cos

(i - 1)n

n

-to0 t -Ф0

x_n = R cos

(n - 1)n

n

-to0 t -Ф0

Начальные условия для перемещения и линейной скорости: ^x 1⁽⁰⁾ = x 10 , dx

— ⁽⁰⁾ = v _w.

dt

Отсюда

x cos Ф0 = —

Ф_о = arccos — = arcsin. 1 - x ¹⁰

0 R R 2

- R to 0 sin( to 0 0 + Ф 0 ) = v _w,

to0 =

v ₁₀

V R ² - x 2

Выводы

Инертные тела массой m каждое осуществляют гармонические колебания, обусловленные взаимным обменом кинетической энергией. Потенциальная энергия пружин для этого не требуется.

Колебания тел являются свободными.

Особенностью мультиинертного осциллятора является то, что частота его свободных колебаний (5) не фиксирована и определяется преимущественно начальными условиями. Эта особенность может оказаться весьма полезной для технических приложений, например, для самонейт-рализации механической реактивной (инерционной) мощности.

n -угольник x ₁, x ₂,..., x_n осуществляет сложное движение – орбитальное вращение вокруг центра координат 0 и спиновое вращение вокруг своей оси, проходящей через центр r .

При этом каждый груз совершает линейные гармонические колебания вдоль своей направляющей. Его координата изменяется от + R до – R .

При расположении направляющих грузов не в виде звезды, а параллельно друг другу углы между соответствующими кривошипами необходимо составят 360/ n градусов.

Мультиинертный осциллятор имеет перспективу промышленного применения. Некоторые вибромашины, в частности сортировальные имеют более трех массивных подвижных рабочих органов. Построение их по схеме мультиинертного осциллятора позволит существенно сократить потребление энергии, которая в этом случае не будет расходоваться на сообщение массивным рабочим органам колебательных движений (около 90 % полной мощности), а будет направлена только на компенсацию трения и на совершение полезной работы.