Математическое моделирование нагрева тонкоплёночных полимеров при их циклической ионно-плазменной металлизации

Гиорбелидзе Михаил Георгиевич, магистрант кафедры производства летательных аппаратов и управления качеством в машиностроении.

электродуговым методом на установке ННВ-6.6И1. Возникающая при этом необходимость получения металлических покрытий с общей толщиной 1…10 мкм для достижения заданного сопротивления резистивного слоя приводит к значительному разогреву полимерной плёнки, что в свою очередь требует разработки и оптимизации термического цикла наращивания покрытия для поддержания допустимого диапазона изменения температуры конденсации при максимальной производительности процесса.

В настоящей работе приведены некоторые результаты исследования условий получения оптимального цикла изменения температуры при циклическом нанесении покрытия на тонкоплёночный полимер.

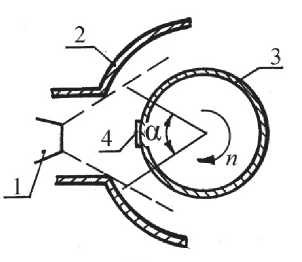
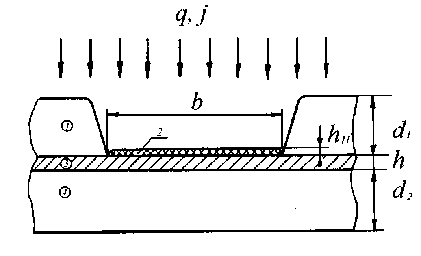
В рассматриваемом технологическом процессе [2, 5] тонкоплёночный полимер располагается внутри металлического приспособления, состоящего из основания и маски с щелевыми отверстиями, через которые происходит осаждение покрытия и формируется заданный топологический образ резистивного слоя. Схема осаждения покрытия и схема поперечного сечения маски в области щелевого отверстия приведены на рис. 1.

В такой схеме напыления маска совершает вращательное движение в вакуумной камере с частотой вращения n и за период вращени t_П в течение времени t_Н=k_Н . t_П находится в зоне напыления (рис. 1а), а в течение времени t_охл =(1- k_Н ) . t_П вне этой зоны, где к Н = а /36° ° С, а - угловая ширина зоны напыления (рис.1а). Некоторые параметры процесса наращивания покрытия приведены в табл.1.

• а)                                                        б)

Рис. 1. Схема осаждения покрытия (а) и схема поперечного сечения маски в области щелевых отверстий (б)

На рис.1а: 1 – катод, 2 – стенки анода генератора и вакуумной камеры, 3 – вращающееся цилиндрическое приспособление для закрепления масок, 4- маски с полиимидной плёнкой.

На рис. 1б: 1– маска с щелевыми отверстиями, 2 – покрытие, 3 – полиимидная пленка, 4 – основание маски

Таблица 1. Некоторые параметры процесса наращивания покрытия на вращающейся полиимидной пленке

№	Материал покрытия	ХН65МВ
1	Ток дуги, I д , А	70			120
2	V П , мкм/мин	0,30			0,52
3	V , мкм/мин ср	0,058			0,100
4	n , об/мин	2	7,5	12	2	7,5	12
5	Период вращения, t П , с	30	8	5	30	8	5
6	t н , с	5,8	1,6	0,97	5,8	1,6	0,97
7	h 01 _ V n " t H , нм	29	8	4,8	50	14	8,4
8	N ( об ) для h =5 мкм	172	625	1042	100	357	595
9	t ( мин ) для h =5 мкм	86			50

Примечание: V П – скорость роста покрытия на неподвижной детали; V ср – средняя скорость роста покрытия на вращающейся детали; t н – время напыления за один оборот; h ₀₁ – толщина слоя наращиваемая за один оборот; N и t – полное число оборотов и время, необходимое для выращивания покрытия толщиной 5 мкм

При нахождении щелевого отверстия в зоне напыления на полимерной плёнке наращивается покрытие толщиной 5…50нм (табл.1) и, из-за действия теплового потока плазменной струи с плотностью q , плёнка с покрытием нагревается до некоторой температуры T₀₁ . При выходе щелевого отверстия из зоны напыления наращивание покрытия прекращается, величина q обращается в ноль и плёнка с покрытием из-за теплообмена с технологическими приспособлениями остывает до некоторой температуры T_охл . Задачей оптимизации термического цикла напыления является определение условий, при которых при каждом цикле напыления величины T₀₁ и T_охл принимают постоянные значения и лежат в диапазоне между заданными минимальным T_М,1 и максимальным T_М,2 значениями температуры.

Для решения поставленной задачи найдём изменение температуры системы покрытие-плёнка за период совершения одного полного оборота приспособления в вакуумной камере.

Учитывая, что геометрические параметры сечения (рис.1б) удовлетворяют условиям L » b » h » h _n 1 , задачу математического моделирования нагрева и охлаждения системы покрытие-полимер можно рассматривать как нагрев и охлаждение двухслойной пластины в одномерной постановке с координатой z по ее толщине.

В общем случае, задача математического моделирования процесса изменения температуры тонкой полиимидной пленки, расположенной в массивном технологическом приспособлении, при наращивании металлического покрытия должна состоять из двух уравнений теплопроводности для пленки и наращиваемого металлического покрытия, граничного условия второго рода на наращиваемой поверхности, граничных условий четвертого рода на границе полимер-покрытие, граничного условия третьего рода на поверхности полимера, контактирующего с поверхностью технологического приспособления и начального условия.

Однако, учитывая, что за один цикл наращивания покрытия параметр Фурье тепловой задачи удовлетворяет условию

Fo ₁ = a ₁ t/h - ( t ) = a ₁ jh_- •V_- >  4,5 ■ 10⁷ , можно считать распределение температуры по сечению наращиваемого металлического покрытия постоянным и свести двухслойную задачу теплопроводности к однослойной задаче, решение которой не представляет значительных сложностей [6]. Вместе с тем, учитывая, что величина критерия Био в этой задаче значительно меньше единицы, а времена завершения цикла напыления и цикла охлаждения соответствуют параметру Фурье задачи, величиной значительно превышающей единицу, можно показать, что изменение температуры системы покрытие-полимерная плёнка с погрешностью не превышающей одного процента описывается приближёнными соотношениями на этапе нагрева и последующего охлаждения:

Т н ( Fo ) = T o + [ ( qh A Bi ) - ( T , - T ) ] ( 1 - e ^- BiFo ) . (1) Т ( Fo) = T - ( Т 01 - Т ) ( 1 - e ^- ' ) . T oi = Т н ( FO h ) . (2) где Т 0 - начальная температура системы, Bi = ah/ A - критерий Био; F 0 - at/h² - критерий Фурье; a . A - коэффициенты температуропроводности и теплопроводности полимерной плёнки, h – её толщина. а и Т - параметры теплообмена полимерной плёнки с технологическим приспособлением, которые должны определяться из экспериментальных данных.

Учитывая плотность теплового потока при данном виде напыления прямопропорциональна скорости наращивания покрытия q = gV_П соотношениям (1) и (2) можно придать вид:

Тн (t) = Tо + [AV- - (Tо - Tc )](1 - e-A2t), (3)

Т (t) = T01 -(Т01 - Тс )(1 - e- A2 t), T = Тн (tH). (4) где A1 = g/а; A 2 = а- a/Ah .

Таким образом, в соответствии с рассматриваемой кинетической схемой технологическое приспособление с полиимидной пленкой движется по окружности в вакуумной камере и в момент времени t =0 с начальной температурой пленки T ₀ попадает в зону действия плазменной струи. В момент времени t = t н = k _H t _п её выхода из этой зоны температура пленки примет значение (3):

Т (t) = Т. = T +[AV-(T -T)](1-e-A2). (5) н н 01      0       1 п 0 c

При её дальнейшем вращении и завершении полного оборота и охлаждения в течение времени t = t = (1 - к _н ) t _п её температура в соответствии с (4) будет:

Т(t„)=Т((1-кн)■ tn)=Т -(T0 -T)(1-e-A2"-k‘-).(6)

Подставляя (5) в (6) и проведя необходимые преобразования получим, что изменения температуры пленки от момента её входа в зону напыления до момента её входа в эту зону после совершения одного оборота вращения определяется соотношением:

Т(t„„)-Т = e-A2tn[AV(eA' -1)-(T0-T)-(eA21- -1)]. (7)

Аналогично, рассматривая некоторый ( i + 1 )-ый оборот вращения получим, что в любом цикле вращения изменение температуры пленки от момента её входа в зону напыления Т ( t o_хл i ) до момента её входа в эту зону после совершения полного оборота Т ( t_ox , i ₊ 1 ) будет

ДТох, (i+1, i ) = Т(tox.i+1) - Т (<ох„.) = e - A2'- ■

■ [ AV - ( e A ^{2 к н}'^- - 1 ) - ( Т(t ox, , ) - Т с ) - ( e A ² -^- - 1 ) J ⁽⁸⁾ где i -0.1.2..; T ^(t _la ,0 ⁾= ^T 0 .

Из (7) видно, что в рассматриваемой схеме нанесения покрытия в зависимости от периода вращения t П (или частоты вращения n ) возможны три варианта изменения температуры пленки в момент её повторного входа в зону напыления:

T (t )= T ; T (t )> T ; T (t )< T . (9) x ox, /         0 ’       X ox, /        0 ’ X ox, /        0       x z

В первом случае T ( t_ox , ) = T ₀ из (8) видно. что с первого цикла вращения плёнка с постоянной температурой T ₀ входит в зону напыления и постоянной температурой (5) выходит из этой зоны. Условием выполнения этого оптимального цикла напыления, будет условие, вытекающее из (7):

A 1 V - ( e A ^{2 k}- t ^п - 1 ) = ( Т 0 - Т_с ) - ( e A ² t ^- - 1 ) .(10) а также ограничение на температуру нагрева (5) после выхода из зоны напыления:

Т.., > T0 +[ AV --(Т 0 - Т. )](1 - e- A2 k't- ).(11)

Это соотношение (10) можно рассматривать как уравнение для нахождения оптимального значения t (или ) в зависимости от

-,onm x        onm '

трёх параметров

Г = А ^ з^-^

¹ Т - Т

0 с

= ^gv - = q л „ат z

ОТ 0 - Т_с ) а ( Т , - Т_с ) , A ² = Ah , k н . ⁽¹²⁾

Во втором случае условие T (tox, ) > T0 приводит к тому. что АТox, (i +1, i) в (8) больше нуля и T (tox, , i) растёт с ростом i. Следовательно. наступит такой цикл вращения i=s, при котором убывающая положительная разность слагаемых в квадратных скобках (8) обратится в ноль. В результате при дальнейшем вращении температура пленки T (tox, s ) при её входе в зону напыле- ния будет принимать постоянное значение, определяемое из (8) соотношением:

тL,,)-Т. + AVn (еА2k'" - 1У(еА2" -1). (13)

Видно, что этот случай реализуется при <  t (или n >  n ).

П П , опт               опт

Используя (5), легко показать, что при выходе из зоны напыления в каждом последующем цикле температура полимера будет принимать также постоянное значение, определяемое соотношением:

Tt,„ +1. )= Т + AV (1-е- А2 k* )/(1-е-АП). (14)

В третьем случае T ( t ох ) < T 0 снижение температуры плёнки в момент её входа в зону напыления приводит к тому, что А Т охл ( i + 1, i ) в (8) меньше нуля и T ( t, i ) убывает с ростом i . Следовательно, наступит такой цикл вращения i=s₁ , при котором убывающая по абсолютной величине отрицательная разность слагаемых в квадратных скобках (8) обратится в ноль. В результате при дальнейшем вращении температура плёнки T ( t ох» s ) при её входе в зону напыления также будет принимать постоянное значение, определяемое тем же соотношением (13), а при выходе из зоны напыления её температура будет определяться соотношением (14). Видно, что этот случай реализуется при t _п >  t _п , _оит (или n <  П опт ).

Таким образом, при циклическом напылении на вращающееся изделие может существовать оптимальная частота вращения n опт , при которой изменение температуры плёнки с первого цикла вращения изменяется в пределах от T ₀ до T . ( t . ) <  T_{м 2} . Эта оптимальная частота определяется условиями (10) и (11) и зависит от трёх обобщённых параметров режима (12). При выборе значения частоты вращения больше или меньше оптимальной через некоторое число циклов вращения также наступит режим, при котором температура плёнки будет также в каждом цикле вращения изменяться в постоянных пределах от Т ⁽ t _о„ ^ ) (13) до Т ^{( t}_о„ , ⁺ t . ^{) (14)} и если эти пределы удовлетворяют условиям

T . < T (t    ), T (t    + t )< T ,, (15)

м 1 н охл s охл s н м 2

то и эти режимы можно использовать для нанесения покрытия.

Определим оптимальную частоту вращения n опт .

Анализ (10) показывает, что решение этого уравнения существует только при выполнении определенного соотношения между параметрами (12). Действительно, один корень уравнения имеет тривиальное значение tП =0. Поэтому нетривиальный корень решения tП > 0 будет существовать только в том случае, когда график левой части уравнения (10) с •. < 1 располагается выше графика правой части этого соотношения, что приведёт к их пересечению во второй точке с tП > 0. Следовательно, производная левой части соотношения (10) по tн в точке tП =0 должна быть больше производной правой части этого соотношения в той же точке, то есть:

г • = А1НПк^ =   qk н > 1.

1 н Т0 - Т. «(Т0 - Т.)

В частности из этого соотношения вытекает, что если период вращения t П удовлетворяет условию А 2 1 П <<  1 , то не существует решения уравнения (10). Действительно, используя условие А 2 t _п <<  ¹ , получим Г 1 • . = 1 , что противоречит (16). Приведенный пример показывает, что часто используемый в технологии, казалось бы очевидный, экспериментальный подход определения оптимального цикла изменения температуры изделия при импульсных мощных тепловых потоках за счет выбора больших оборотов вращения изделия (малые значения t П ) не даст желательного результата без учета соотношения (16).

Полученные результаты использованы для стабилизации термического цикла получения наноструктурного покрытия из материала ХН65МВ на полиимидной плёнке толщиной h =60 мкм. Из предварительных экспериментальных исследований было получено, что плотность теплового потока плазменной струи связана со скоростью конденсации покрытия соотношением q =6,8•10³ • V_П ( в данном соотношении V_П измеряется в мкм/мин), параметры теплообмена для данных условий напыления составляют а =(11,3±0,2) Вт/м²К и Т с =(38±5)⁰С, а границы диапазона температур для получения качественного покрытия на полиимидной плёнке должны составлять Т_М,1=Т₀= 80⁰С и Т_М,2= 160⁰С.

На рис. 2 приведен график корней уравнения (10) в зависимости от параметра Г ₁ при А ₂ =0,107 и k н =0,194. Этот график периода вращения t П опт или частоты вращения n опт даёт значения этих параметров при оптимальном цикле изменения температуры полиимидной пленки для выбранных значений параметров Г ₁ , А ₂ и k н . Например, для технологического режима при скорости нанесения покрытия V П =0,5 мкм/мин значение параметра Г ₁ составляет Г ₁ =7,33, что даёт период вращения t П опт =7,6 с и частоту вращения n опт =7,9 об/мин. Используя эти данные, проверяем выполнение условия (1 1) Т . ( t . ) = T + [ AV " - ( Т 0 - Т . Х1 - e ^- A²•.-"" ) = 120 ⁰ C< T м,2 .

Так как это условие выполняется, то для режима напыления материала ХН65МВ на токе дуги 120А при скорости напыления V П =0,5 мкм/ мин на полиимидную пленку в разработанном технологическом приспособлении следует установить частоту вращения n опт =7,9 об/мин при условии начального подогрева пленки до T ₀ =80єС. При этом за один оборот приспособле-

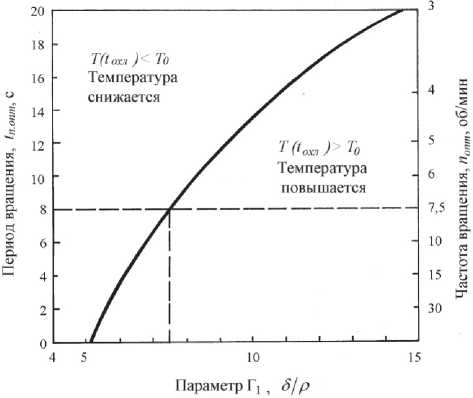
Рис. 2. Период t П _, опт и частота вращения n опт при оптимальном цикле изменения температуры полиимидной пленки в зависимости от параметра Г 1 = q Iа ( Т 0 - Т с ) при к н =0,194 и А ₂ =0,107

пределах от 60 єС до 160 єС обеспечивается при рассеивании параметров режима в пределах не более 20%. Следовательно, разработанная схема циклического напыления изделий, расположенных на вращающемся цилиндрическом технологическом приспособлении является устойчивой к рассеиванию параметров режима напыления.

Таким образом, проведенные исследования позволили разработать адекватное теоретическое описание изменения температуры полиимидной пленки в процессе нанесения покрытия и её охлаждения в вакуумной камере, адаптировать эти результаты к конкретной технологической ситуации нанесения покрытия на изделия, расположенные на цилиндрическом технологическом приспособлении, вращающемся вместе с каруселью вакуумной камеры, получить исходные соотношения для определения частоты вращения, при которой реализуется оптимальный цикл изменения температуры полиимидной пленки в таком процессе нанесения покрытия и предложить эффективный приём управления температурным циклом за счет изменения скорости вращения.

ния будет наращиваться слой толщиной около 0,013 мкм=13 нм и для получения слоя общей толщиной, например, 5 мкм должно быть совершено примерно 385 оборотов или общее время нанесения покрытия должно составить около 52 мин.

Отметим, что если при напылении будет установлена частота вращения n >  П , то будет реализована ситуация, определяемая вторым условием (9) и температура пленки по мере её вращения будет от оборота к обороту повышаться пока не примет значение (13), если же будет установлена частота вращения n <  П_опт , то будет выполняться третье условие (9) и температура пленки будет по мере её вращения понижаться до тех пор пока не достигнет значения (9). Установленная закономерность позволяет предложить очень эффективный приём управления термическим циклом нанесения покрытия на вращающиеся изделия. Если в процессе нанесения покрытия оптической системой регистрации температуры устанавливается, что от оборота к обороту температура изделия повышается, то для её уменьшения необходимо уменьшить частоту вращения, если же понижается, то увеличить частоту вращения. Причём это необходимое изменение частоты может быть подобрано экспериментально несколькими этапами её изменения, либо рассчитано по приведенным соотношениям.

Численный анализ допусков на точность определения величины n в зависимости от точ-опт ности определения параметров (12) по условиям (15) показывает, что рассматриваемый режим напыления с изменением температуры плёнки в

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0072 «Получение нового вида высокоомных материалов в виде наноструктурных полиметаллических покрытий на тонкоплёночных полимерах для изготовления высокоэффективных малогабаритных электронагревателей систем терморегулирования космических аппаратов».