Математическое моделирование нагруженной распределенной нагрузкой цилиндрической арматуры в различных направлениях
Автор: Ташполотов Ы., Маматов Э.У.
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Естественные науки
Статья в выпуске: 11 т.10, 2024 года.
Бесплатный доступ
Рассматривается математическое моделирование напряженно-деформированного состояния цилиндрической арматуры, нагруженной распределенной нагрузкой в различных направлениях. Основное внимание уделяется определению внутреннего напряжения и закона его распределения для арматуры, созданной на основе базальтовых горных пород. Построена математическая модель, включающая уравнения движения, условия прочности, а также связь между напряжением и деформацией.
Математическое моделирование, базальтовая арматура, напряженно-деформированное состояние, нагрузка, уравнения движения, условия прочности
Короткий адрес: https://sciup.org/14131416
IDR: 14131416 | DOI: 10.33619/2414-2948/108/01
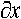
Список литературы Математическое моделирование нагруженной распределенной нагрузкой цилиндрической арматуры в различных направлениях
- Karsh P. K., Mukhopadhyay T., Dey S. Spatial vulnerability analysis for the first ply failure strength of composite laminates including effect of delamination // Composite Structures. 2018. V. 184. P. 554-567. DOI: 10.1016/j.compstruct.2017.09.078
- Gholizadeh S. A review of non-destructive testing methods of composite materials // Procedia structural integrity. 2016. V. 1. P. 50-57. DOI: 10.1016/j.prostr.2016.02.008
- ГОСТ Р 51372-99. Методы ускоренных испытаний на долговечность и сохраняемость при воздействии агрессивных и других специальных сред для технических изделий, материалов и систем материалов. ГОСстандарт России. ИПК Издательство стандартов, М., 2000. 63 c.
- Zheng J., Maharaj C., Liu J., Chai H., Liu H., Dear J. P.A comparative study on the failure criteria for predicting the damage initiation in fiber-reinforced composites // Mechanics of Composite Materials. 2022. V. 58. №1. P. 125-140. DOI: 10.1016/j.prostr.2016.02.008
- Егоров В. И. Применение ЭВМ для решения задач теплопроводности. СПб, 2006.
- Гриневич Д. В., Яковлев Н. О., Славин А. В. Критерии разрушения полимерных композиционных материалов (обзор) // Труды ВИАМ. 2019. №7 (79). С. 92-111. DOI: 10.18577/2307-6046-2019-0-7-92-111
- Деревянко В. Н., Саламаха Л. В., Кушнир Е. Г., Щудро Е. С., Смоглий А. Г. Стойкость базальтовых волокон в различных средах // Вiсник Приднiпровської державної академiї будiвництва та архiтектури. 2010. №2-3. С. 33-38.
- Милованов С. А., Маркин В. Б. Применение базальтовых волокон для созданиясоединений "металл-композит" // Ползуновский вестник. 2018. №2. С. 135-139. DOI: 10.25712/ASTU.2072-8921.2018.02.025
