Математическое моделирование напряженного состояния неоднородной полосы с наружным макродефектом

Измерение распределений напряжений в неоднородных образцах и конструкциях с осложненной геометрией, в том числе при наличиии дефектов, вызывает в натурных экспериментах труднопреодолимые сложности. В то же время среднеинтегральные по нетто-сечениям напряжения легко находятся через измерения критических нагрузок. Определение местных напряжений опосредовано, на основе измерения деформаций, основывается на теории малых деформаций, неприменимой к упрочняемым, то есть реальным, материалам. С другой стороны, знание распределения напряжений в различных частях конструкций необходимо для оценки несущей способности этих конструкций. Поэтому актуально теоретическое, на основе разработки адекватных математических моделей, исследование напряженного состояния этих конструкций. Возникающие в этих моделях граничные задачи для нелинейных уравнений в частных производных требуют для их изучения разработки соответствующих аналитических и численных методов. В работе рассматривается напряженное состояние неоднородной полосы с наружним макродефектом в более прочной части или на границе между более прочным и менее прочным участками под растягивающей нагрузкой (см. рис. 1, а). Граница между более прочной и менее прочной частью (контактная граница), как часто бывает в реальных сварных соединениях, не предполагается ортогональной напрявлению нагрузки. Более прочная часть испытывает в процессе пластического деформирования ослабляющее влияние менее прочной части. Изучение напряженного состояния таких неоднородных соединений необходимо для определения прочностных свойств реальных сварных соединений, содержащих наклонные контактные границы и дефекты различной формы и расположения [1–4]. Краевая задача для системы уравнений гиперболического типа (при плоской деформации) относительно компонент тензора напряжений, моделирующая напряженное состояние на более прочном участке, оказывается переопределенной [5, 6], следствием чего является разрывность ее решения и негладкость характеристик. Линии разрыва напряжений определяются формой границы и граничными условиями [5, 6]. Цель работы – на основе численного решения [7] задачи сопряжения для напряжений на контактной границе и исследования полей характеристик описать напряженное состояние неоднородной полосы с наружным макродефектом и, как следствие, получить алгоритмы и программы для нахождения критической нагрузки в зависимости от параметров соединения: размеров и расположения дефекта, угла наклона контактной границы и коэффициента механической неоднородности соединения. Заметим также, что решение [7] задачи сопряжения для напряжений на контактной границе позволило установить критерий вовлечения более прочной части соединения в пластическое деформирование в зависимости от угла контактной поверхности и коэффициента контактного упрочнения (рис. 1, б).

Рис. 1. а) Варианты расположения дефекта. б) Критерий вовлечения более прочной части соединения (основной металл) в пластическое деформирование в зависимости от угла наклона контактной поверхности α и коэффициента K контактного упрочнения

Уравнения равновесия для напряжений на контактной поверхности в безразмерных координатах имеют вид:

° = ^K" ; ' = К' ; K = k ⁺ /k ^- , (1)

где k ⁺ и k ^- - параметры пластичности более прочного и менее прочного участков соответственно. Здесь ( X ; у' ) - декартовы координаты с осью Ox ’ , направленной вдоль контактной границы. Будем называть уравнения (1) условиями сопряжения . Задача сопряжения [7] для напряжений на контактной границе формулируется так:

на основе граничных условий и заданных на контактной поверхности условий сопряжения (1) для напряжений найти напряжения σ _y ^± ′ и τ _x ^± ′ _y ′ на контактной поверхности.

В работе [6] установлен количественный критерий вовлечения материала более прочного участка в процесс пластического деформирования. В частности, показано, что если угол наклона контактной поверхности к направлению, ортогональному направлению нагрузки, равен нулю, то более прочный материал начинает течь при K < 2. В общем случае метод основан на ограниченности угла ω- поворота характеристик в менее прочной части величиной п/4 — а. С увеличением внешней нагрузки угол ш- возрастает от нуля до тех пор, пока выполняется неравенство ш < п — а, либо в какой-то момент более прочный материал перейдет в пластическое состояние, и рост угла ш- прекратится. Углы поворота характеристик ш- и ш+ связаны с напряжениями на контактной поверхности уравнениями y+ = 1 — 2ш+ + cos 2ш+, yy = 1 + 2ш + cos 2ш .

Используя условия сопряжения (1), эти уравнения и представляя неизвестные функции ш - и ш ⁺ в виде степенного ряда по параметру А = K — 1 :

ш = Е шк Ak, ш+ = Е ш+Ак, получим решением трансцендентной системы уравнений [7] аналитические выражения для вычисления углов ш- и ш+. Эти выражения имеют в общем случае (когда а = 0) громоздкий вид:

ω ^-

1 + cos 2 α + sin 2 α

4 cos 2 α

8 cos 2α

sin ² 2а + sin 2а „

--------2^------А2 + ...

cos ² 2а

1 + cos 2а — sin 2а ш ⁺ =----Й-----А +

4 cos 2α

- tan 2а —

^{1    1}    +1     ¹

8 cos 2α

— sin 2а

+1

cos ² 2а

)]

А ² +...

В работе [7] разработан алгоритм численного решения упомянутой системы методом итераций. Написанная на его основе в среде MATLAB программа позволяет вычислять значения нормальных и касательных напряжений на контактной границе в зависимости от параметров α и K в критический момент нагружения (т.е. в момент начала течения при-контактной зоны более прочного участка соединения).

Наклон контактной поверхности и расположение относительно этой поверхности дефекта приводят к большому разнообразию распределения напряжений по нетто-сечению (рис. 2). Сложность исследования напряженного состояния такого соединения обусловлена также разрывностью напряжений в более прочной части [6] (на рис. 2 пунктиром показана линия разрыва нормальных напряжений). Различие ситуаций определяется расстоянием g между точками выхода на свободную поверхность контактной поверхности и нетто-сечения, точнее зависимостью g от параметров m , а , ш ^- и ш ⁺ . На рис. 2 а показана одна из наиболее сложных ситуаций, когда нетто-сечение пересекает контактную границу, и на эпюру напряжений по нетто-сечению влияют искажения полей характеристик как в более прочной, так и в менее прочной части, возникшие в результате взаимного воздействия этих частей под нагрузкой в критический момент нагружения. Здесь эпюра напряжений может иметь шесть участков, на которых величина напряжения определяется различными зависимостями (см. рис. 2 а). Длина каждого участка зависит от соотношения между величинами g , m , а , ш ^- и ш ⁺ . Углы ш ^- и ш ⁺ зависят, в свою очередь, от угла а и коэффициента контактного упрочнения K . На основе этих соотношений и алгоритмов работ [6, 7] написана программа для вычисления среднего критического напряжения в данной ситуации.

На рис. 2 б показан другой сложный случай, при котором нетто-сечение не пересекает контактную границу. В этом случае на эпюру напряжений по нетто-сечению влияют искажения полей характеристик в более прочной части, возникшие в результате воздействия менее прочной части под нагрузкой в критический момент нагружения, и расстояния g между точками выхода на свободную поверхность контактной поверхности и нетто-сечения. Анализ полей характеристик (линии скольжения, см. рис. 2) показывает, что возможны три подслучая, определяемые зависимостями между параметрами g , m , а и ш ⁺ :

m(1 — tan а)(1 + %-)

g > —'------+--- ,                      (2)

3 + tan а + Щ2—(1 — tan а)

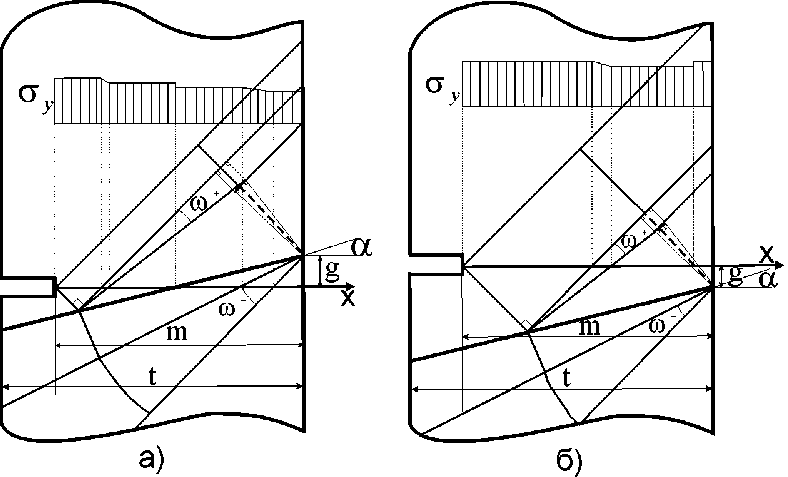
Рис. 2. Поле характеристик и эпюры напряжений

m(1 — ^+ — tana(1 + 3^ ' ))        m(1 — tana)(1 + ^-)

------+-------------< g <----------+----²— ,          ⁽³⁾

3 — ^2—+ tan a(1 — 2 w + )        3 + tan a + ^- (1 — tan a)

m(1 — ^+ — tan a(1 + 3 w + ))

g <------- + ------------^----.                          (4)

3 — ^2—+ tan a(1 — 2 w ⁺ )

Случай (4) приводит к ситуации, соответствующей рисунку 2, б). В каждом из случаев (2) – (4) эпюра напряжений по нетто-сечению имеет несколько участков, размеры которых и напряжения на них определяются несложными, но очень громоздкими вычислениями, которые здесь не приводятся. На их основе и алгоритме работы [6] описан и реализован в программе алгоритм для вычисления среднего критического напряжения в ситуациях (2) - (4). Полученные результаты для наружного дефекта глубины 0,1t , расположенном на расстоянии g = 0, 2t ( t - толщина полосы) от контактной поверхности, представлены на рис. 3.

Если a = 0 , то возможно в некоторых ситуациях получение среднего критического напряжения в аналитической форме [6].