Математическое моделирование нестабильности позвоночника и методов стабилизации
Автор: Орлов С.В., Седов Р.Л., Бобарыкин Н.Д., Аполлинариев В.И.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 3 (49) т.14, 2010 года.
Бесплатный доступ
К одному из наиболее важных вопросов биомеханики позвоночника относится нестабильность сегментов кинематической цепи позвоночника. По мнению американского физика Ильи Пригожина (1991), «нестабильность» - это состояние системы, характеризующееся неоднородностью и разновремённостью каждого из протекающих процессов и всех изменений в целом. Это определение справедливо и для механической системы позвоночного столба. В свою очередь, нестабильность позвоночного столба - это мультикаузальная проблема, которая может встречаться в любом возрасте. Причинами этой патологии могут быть как травмы с повреждением опорных структур позвоночника, так и воспалительные деструктивные процессы (остеомиелит, туберкулез), онкологические поражения позвонков, аномалии развития, дегенеративные поражения межпозвоночных дисков или связочного аппарата. Изучение природы нестабильности методом математического моделирования имеет важное прикладное значение, так как предлагает биомеханическое обоснование хирургической коррекции этой патологии, оптимизирует выбор клинических решений для типичных вариантов нестабильности. Это актуально как для врачей различных специальностей (ортопедов-травматологов, нейрохирургов, неврологов, фтизиатров, онкологов), так и для инженеров-технологов, разрабатывающих позвоночные импланты и фиксаторы. При помощи модели изучены основные формы нестабильности позвоночника при травмах, а именно повреждения сгибательного типа, разгибательного типа и ротационные. Предложены биомеханически обоснованные варианты хирургической коррекции типичных вариантов нестабильности, приведены расчёты оптимальных параметров стабилизирующих конструкций. Доказано преимущество применения демпфирующих (полуригидных) конструкций по сравнению с жёсткими.
Нестабильность позвоночника, математическая модель, оптимизация методов стабилизации позвоночника, фиксирующие устройства
Короткий адрес: https://sciup.org/146215998
IDR: 146215998 | УДК: 531/534:
Текст научной статьи Математическое моделирование нестабильности позвоночника и методов стабилизации
Под нестабильностью позвоночника подразумевают такое нарушение взаимодействия между телами позвонков, когда вследствие сугубо механических причин изменяются нормальные законы статики и кинетики позвоночного столба на определенном участке, что проявляется в избыточной и аномальной подвижности тел, некорректных их перемещениях, выходящих за физиологические пределы ( R. Louis , © Орлов С.В., Седов Р.Л., Бобарыкин Н.Д., Аполлинариев В.И., 2010 Орлов Сергей Владимирович, к.мед.н., директор Института биомеханики позвоночника и суставов, Калининград
Седов Роман Леонидович, аспирант, ассистент кафедры прикладной математики, Калининград Бобарыкин Николай Дмитриевич, д.т.н., профессор кафедры прикладной математики, Калининград Аполлинариев Валерий Иванович, к.т.н., заведующий кафедрой прикладной математики, Калининград
-
1983, R. Fergusson , 1988). Это может являться причиной многочисленных сугубо медицинских проблем, часто требующих хирургических методов лечения ( Ulrich A. Wagner , 1998, Thomas R. Haher , William Tallman Felmly , Michael O'Brien , 1991).
Для правильного решения важной практической задачи – хирургического лечения нестабильности позвоночника необходимым условием является оптимальный подбор корригирующих фиксирующих приспособлений, способных предотвратить некорректные перемещения тел позвонков и одновременно максимально точно протезировать упругие и динамические характеристики связочно-капсульного аппарата позвоночника, что позволяет сделать математическая модель трехпозвонкового комплекса человека. В работе [3] подробно описана математическая модель трёхпозвонкового комплекса человека при фиксации позвонков жесткими пластинами. В настоящей работе предлагается оптимизация применения жестких фиксирующих пластин и показано преимущество гибких или полуригидных фиксаторов.
В основу модели положено математическое описание динамических процессов дифференциальными уравнениями Лагранжа II рода, составленных на основе расчетной схемы трехпозвонкового комплекса, представленного дискретными сосредоточенными массами, связанными вязкоупругими элементами и обладающими определенными геометрическими параметрами [1].
Цель исследования – при помощи математической модели трёхпозвонкового комплекса человека провести расчёт и оптимизацию механических свойств применяемых фиксаторов.
За основу был принят принцип стабильности позвоночного столба, изложенный L. Rene [8], где стабильность позвоночника представлена в вертикальной, горизонтальной и аксиальной плоскостях (ротация), что обеспечивается телами позвонков с дугоотростчатыми суставами, которые связаны между собой упруго-демпфирующими элементами (межпозвоночные диски, мышечно-связочный аппарат).
Механическая система обладает следующими свойствами:
-
1. Механическая система является диссипативной.
-
2. Распределение нагрузок соответствует трехстолбовой концепции F. Denis [6].
-
3. Предел прочности тел позвонков и упругодемпфирующих элементов, а также их упругая деформация и плотность считались условно установленными по данным работы [1].
-
4. Изменение геометрических характеристик трехпозвонкового комплекса соответствовало типичным типам статико-динамических нарушений стабильности позвоночника [2, 6].
Конструктивная трёхпозвонковая модель
Расчетная схема фрагмента позвоночника человека, состоящая из трех позвонков с клиновидным средним позвонком и стабилизирующими конструкциями, представлена на рис. 1 с вариантом клиновидной деформации среднего позвонка и двумя стабилизирующими конструкциями (для передних и задних опорных комплексов).
Здесь введены следующие обозначения:
J i , М i , X i – момент инерции, масса, координата i -го позвонка ( i = 1, 2, 3);
Cсm j – коэффициенты жесткости j -й стабилизирующей пластины ( j = 1, 2);
Сop j – коэффициенты жесткости j -й опоры ( j = 1, 2);
d 1 = 25 мм; d 2 = 20 мм; d 3 = 5 мм; d 4 = 30 мм;
d 1 ′ = 8,5 мм; d 2 ′ = 26,5 мм; d 3 ′ = 17 мм;
l 1 = 32 мм; l 2 = 10 мм; l 3 = 25 мм; l 4 = 10 мм; l 5 = 50 мм;
m 1 = m 2 = m 3 =0,1 кг;
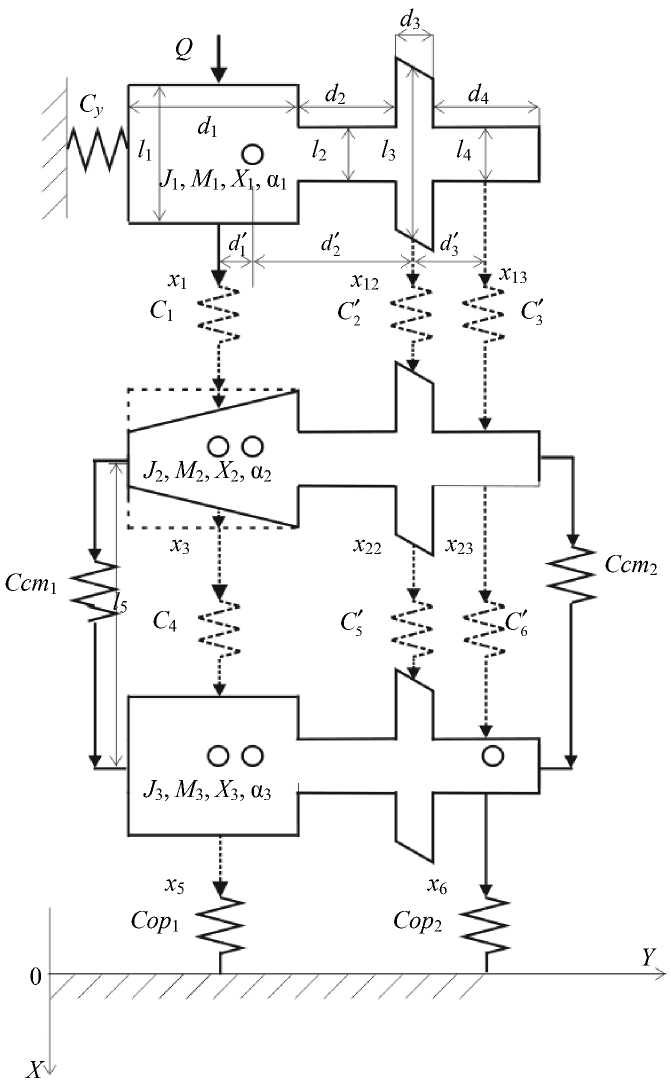
Рис. 1. Расчетная схема трехпозвонкового комплекса с патологией среднего позвонка и ее двухсторонней стабилизацией
J 1 = J 2 = J 3 = 35 кгּ·мм2; Y ц = 17,2 мм; S = 13,25 см2.
Координаты Х ц и Y ц центра тяжести и момент инерции J плоского позвонка определяются формулами:
ц
У X. ■ Y ii i=1_______________,
4 ; ∑ Y i i = 1
Y =
Z X,- Y
= 1___________
∑ X
= 1
;
J = 2 y J J ( X 2 + Y 2) dXdY ,
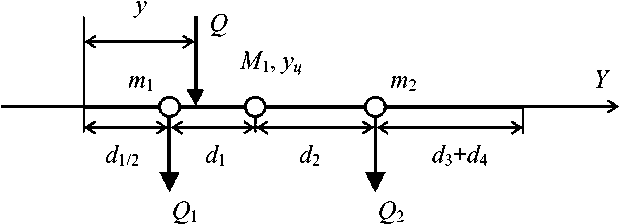
Рис. 2. Распределение сил по оси х
где ( X i , Y i ) – координаты центров тяжести элементарных фигур, составляющих плоский позвоночник, i = 1, 2, 3, 4; γ – удельная поверхностная масса позвонка, кг/мм2.
Для упрощения динамической модели трехпозвонкового комплекса коэффициенты жесткости С 2 и С ‘ , а также коэффициенты жесткости С ‘ и С ‘ приведены к одним коэффициентам С 2 и С 4 (рис. 2), соответственно, по следующим формулам:
С d 2 C ‘ + ( d 2 + d 3 ) C з 2 d 2 + d 3
„ d 2 C 5 + ( d 2 + d 3 ) C 6
С 4 —
2 d 2 + d з
.
На расчетной схеме (см. рис. 2) третий позвонок связывается посредством жестких элементов Сор 1 и Сор 2 с опорой по оси OX , а первый – по оси Y через С y .
Для фиксации вариантов нестабильности позвоночника предусмотрено применение условных жестких плоскостных конструкций с коэффициентами жесткости Сст 1 и Сст 2 , что позволяет моделировать как жесткие ригидные металлические системы, как и полуригидные пружинные элементы.
Математическая модель трёхпозвонкового комплекса
Разработанная математическая модель позволяет на основе вычисления внутренних нагрузок опорных комплексов каждого позвонка трехпозвонкового комплекса рассчитывать варианты переломов и нестабильности позвонков в различных зонах при их патологии. Кроме этого, можно произвести расчет смещения позвонков по оси Oy под воздействием силы Q 2 y , что чаще всего является причиной стеноза позвоночного канала и может приводить к сдавливанию дуального мешка. Выбранная динамическая модель трехпозвонкового комплекса человека (см. рис. 2) является механической системой, для которой уравнения Лагранжа II рода имеет вид
- (- ^ dt ( д xck v
д П д Ф д T
+ + - — Q k , к = 1, 2,^, 7,
дxk дxk дxk где Т, П – кинетическая и потенциальная энергия системы;
Ф – диссипативная функция, определяемая спинными мышцами;
Q k – внешние воздействия.
В качестве обобщенных координат x k принимаются следующие координаты: х 1, х 2 – абсциссы центров тяжести тела 1-го позвонка и его остистого отростка; х 3 , х 4 – абсциссы центров тяжести тела 2-го позвонка и его остистого отростка; х 5 , х 6 – абсциссы центров тяжести тела 3-го позвонка и его остистого отростка; х 7 = у – ордината центра тяжести тела 1-го позвонка.
Проекции сил Q 1 и Q 3 на оси Х и Y при наличии деформации среднего позвонка трехпозвонкового комплекса человека определяются формулами
Q 1 x = O 2 Q 12 = O 1 Q 12 sin β 1 = Q 1 sin2 β 1 ;
Q 1 y = O 1 O 2 = Q 1 sin β 1 cos β 1 ;
Q 3 x = O 4 Q 31 sin β 3 = Q 3 sin2 β 3 ;
Q 3 y = O 3 O 4 = Q 3 sin β 3 cos β 3 ;
Q2y = Q1y + Q3y = С1Х1sin β1cosβ1 + С3Х3sin β3cos β3, где Q12, Q31 – модули проекций сил на ось X, Oi – вспомогательные точки, обозначающие границы векторов.
Кинетическая энергия механической системы трехпозвонкового комплекса человека, приведенная на рис. 2, равна
T = 1 M,
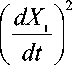
1 dX 1 d α
+ МД 2 +- J + M.L 2 +
2 2 V dt J 2V 2 2 5 dt J
+-• M, ■
1 +1^ Mi I ^
2 i = 1 V dt J
,
f dXt ) f da,. ) _ - 1 о a где I —L I , I —i- I - квадраты скоростей колебаний и вращений 1-го, 2-го и 3-го
V dt J V dt J позвонков относительно центров тяжестей этих позвонков.
Упругие деформации х 1 , х 2 , х 3 , х 4 , х 5 , х 6 центрального и правого столбов 1-го, 2-го и 3-го позвонков связаны со смещениями и вращениями центров тяжестей этих позвонков X 1 , Х 2 , Х 3 и α 1 , α 2 , α 3 следующими соотношениями:
x i = X i - a i d 1 ; x i = X i + a i d 2; i = 1,2,3.
Задача решается в приближении малых смещений, то есть
X i << D i ; tg a i = sin a i = a i .
Тогда X 1 и α 1 выражаются через х 1 и х 2 по формулам (для второго и третьего позвонков аналогично)
a 1 =
х 2
х 1
D 1
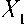
x 2 d 1 + x 1 d
D 1
С учетом соотношения (8) кинетическая энергия трехпозвонкового комплекса с патологией среднего позвонка и его двухсторонней стабилизацией, приведенного на рис. 2, запишется в следующем виде:
Т = m i ( x i )2 + m 2 (? c 2 )L
+ m io x i x 2
+ m з( ^ x 3)2 + m 4(^^4)!.
+ m 20 x 3 x 4 +
+ m 5 (f x 5 ) 2 2
m ( x ɺ )2
+— 6^6 + m 30 :x5 - X 6 +
x M , (y’ )
i = 1
,
z x md2 + J, 4 md2 + J z 4 mdd - J где (mi) = ;(m2) = ^2 ;(mio)i = D)—L.
Потенциальная энергия механической системы трехпозвонкового комплекса человека считается равной нулю при положении статического равновесия, а отсчет деформации упругих элементов ведется от условия, когда статическая нагрузка на элемент уравновешивается упругой силой от его осадки.
В этом случае потенциальная энергия П деформации упругих элементов трехпозвонкового комплекса с патологией среднего позвонка и ее двухсторонней стабилизацией определяется следующим соотношением:
n =
Сор 1 x 5 2
Сор 2 x 6 2
+
C 3 ( x 3
-
x 5)2
C 4 ( x 4 — x 6
+
C i ( X i — x з )
C2(x2 - x4)2 Сст1(х3 - x5)2 Сст2(х4 - x6)2 Сyy2 2 222
Диссипативная функция Ф трехпозвонкового комплекса человека с патологией среднего позвонка и его двухсторонней стабилизацией записывается через коэффициенты демпфирования В j как
Ф =
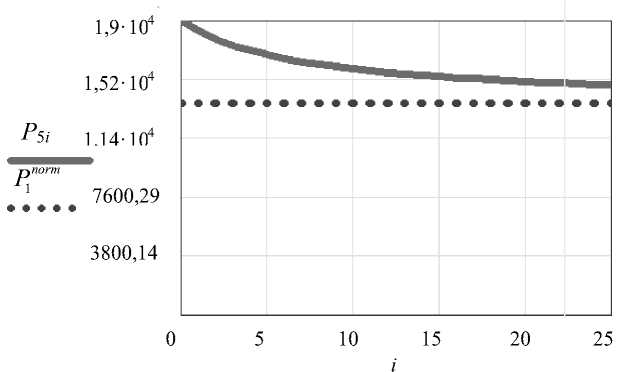
ВоР1(xs) + Вор2(xef + Вз(x3 -xs)2 + В4 BA (x - x )2В2 (x - x )2ВстА (x - x )2Вст (x4 - x)2By (y)2 ।1 13 ।2 24।1 35।2 46।y 22 222 Подставляя значения производных от кинетической и потенциальной энергии, а также от диссипативной функции Ф для механической системы трехпозвонкового комплекса (9)–(11) в уравнения Лагранжа II рода, получим в векторном виде M d2X dt2 + B ■ dX + C ■ X dt = Q, (12) " mici mio 00 0 0 0 1 mio ci m 2 00 0 0 0 0 0 m3c3 m20 0 0 0 где M = 0 0 m20c3 m4 0 0 0 ; 0 0 00 m5 m30 0 0 0 00 m30 m6 0 0 0 00 0 0 Mi+ M2 + M 3 _ " Cici 0 - Ci с 3 0 Ccmi 0 0 " 0 С2 0 -С2 0 00 - Cici 0 (Ci+ С3) с2+ Ccmi 0 -Ccmi- С3 0 0 С = 0 - С2 0 С2 + Ccm 2 + С4 0 -(Ccm2+ С4) 0 ; 0 0 - Ccmi - С3 0 Copi + Ccmi 0 0 0 0 0 - Ccm2- С4 0 Cop2+ Ccm2 0 [ ^i 0 S3 0 0 0 Сy J " B.c. 0 - B1c1 0 B2 0 - B1C3 0 0 - B2 (B1 + B3) с2+ Bcm1 0 Bст1 0 —Bcm.1 — С3 0 0 0 0 " 0 0 B= 0 -B2 0 B2+ Bcm2+ B4 0 -(Bcm2+ B4) 0 B 0 0 -Bcm1- B3 0 Bop1 + Bcm1 0 0 0 0 0 -Bcm2- B4 0 Bop2+ Bcm2 0 _ SB1 0 SB3 0 0 0 B y Q = : Q1 Q2 0 0 0 0 Qey ] Т; Х = [ Х1 Х2 Х3 Х4 Х5 Х6 у]Т где C1 = cos в1, c3 = cos в3, S1 = С1 x1sin e1cos в1, S3= С3x3sinβ3cosβ3 , SB1 = B1 x1sin β1cosβ1 SB3 = B3x3sin e3cos в3. Умножая обе части векторного уравнения (12) на обратную матрицу М–1, получим следующее приведенное векторное уравнение: d-X + M-1 ■ B ■ — + М-1 ■ C ■ X = М-1 ■ Q dt2 dt или d2X dt2 + W ■ — + А ■ X = F, dt где А = М-1■ С ; W = M-1■ В ; F = М-1■ Q. Метод численного решения Система обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами сводится к системе 14 обыкновенных дифференциальных уравнений первого порядка в векторной форме, которая имеет следующий вид: dX dZ + W ■ Z = F - A ■ X. Z; dt dt При этом система дифференциальных уравнений 1-го порядка (14) решается по разностным схемам второго порядка точности по времени 0(τ2): Z - ' j+i τ Z — + W ■ Zj+,= Fj+1 - A-X/; X,+, - X= Zj+1 + Zj; τ j = 0,1, k при начальных условиях X0 = Z0 = 0. Алгоритм численного решения системы векторных уравнений (14) записывается в виде Zj+1 = (1 + tW)-1 ■ (Zj + т(/ - A ■ Xj)); Xj+1 = Xj + 2 (Zj+1 + Z/); j = 0,1,..., k -1. Оптимизация Цель принятия решения – устранение нестабильности позвоночного столба в очаге поражения – трёхпозвонковом комплексе человека с клиновидной деформацией среднего позвонка при помощи фиксации второго и третьего позвонков функциональными пластинами так, чтобы нагрузки на страдающий участок кинематической цепи позвоночника максимально приблизились к физиологической норме. Для этого задаётся поиск минимума отклонения нагрузки P с патологией от нагрузки нормальной Pnorm с сохранением подвижности всей системы. Критерий оптимальности: P5(Q,Cct1,X1,X3,β1,β3)-P5norm → min, P6(Q,Cct2,X1,X3,β1,β3)-P6norm → min, где ∆i = Pi(Q,Ccti,X1,X3,β1,β3)-Pinorm , (i = 5,6) – компоненты двумерного вектора ∆ целевых функций. В силу положительности целевых функций тривиальным решением является нулевое решение. В этом случае нагрузки Pi тождественно приблизились к константам Pinorm , поэтому вырожденное решение является физиологически допустимым. Целевые функции также зависят от параметров С1 и С3 – коэффициентов жесткости межпозвоночных дисков. Эти параметры выбираются для каждой отдельной практической задачи частным образом [5]. В качестве локальной задачи оптимизации выберем нахождение параметров жесткости левой Cct1 и правой Cct2 полуригидных фиксирующих устройств. Таким образом, задача исследования операций в своей постановке полностью отражает структуру и динамику знаний принимающего решение субъекта о множестве допустимых решений и о критерии оптимальности [5]. Приведём результаты расчётов оптимальных параметров пластин. Векторный критерий оптимальности сведён к минимизации следующей целевой функции: P5i P6i Рис. 3. Распределение нагрузок P5 на левый и P6 правый части позвоночного столба Рис. 4. Стабилизация нагрузки P5 (сплошная линия) при оптимизации жесткости пластины 1 при смещении нагрузки на y = 0, P1norm – физиологическая нагрузка в норме (пунктирная линия) Fs = ai pPs -?5*\ + a2 р -Рб*| ^ min, (17) где αi – коэффициенты предпочтения i-го критерия, i = 1, 2. Численный метод оптимизации основан на параллельных вычислениях массивов параметров оптимизации Cct1 и Cct2. На встроенном программном модуле в пакете MathCAD построена программа, реализующая математическую модель нестабильности позвоночника человека. Процедура ypravpoz(x1, x2, …, xn) выполняет нанесение равномерной сетки на плоскость Cct. Вторая процедура pozvon(x1, x2, …, xn, Cct1, Cct2) выполняет численное решение разрешающей системы дифференциальных уравнений в каждом узле сетки плоскости Cct. Задавались следующие исходные данные [10]: С1 = 3,26·103 Н/мм; С2 = 0,92·103 Н/мм; С3 = 0,46·103 Н/мм; С4 = 3,26·103 Н/мм; С5 = 0,92·103 Н/мм; С6 = 0,46·103 Н/мм; Су = 5·103 Н/мм; Cop1 = Cop2 = 3,26· 103 Н/мм; Q = 800 Н (внешняя сила приложена к центру тяжести позвонка при у = 21 мм); β1 = 0,175; β3 = 0,262 (углы деформации среднего позвонка); µ = 1 мм (предел подвижности позвоночника); число временных слоев N = 1000, шаг интегрирования по времени τ = 10–2 с [5]. Как видно из рис. 4, поиск оптимальных жесткостей пластин сопровождается приближением механической системы к нормальному состоянию, близкому к показателям модели при отсутствии деформаций (у здорового человека) [5]. В результате вычислений получен интервал допустимых жесткостей пластин, применяемых для стабилизации позвоночника человека: 350 < Ccm1< 10000 Н/мм, 10 < Ccm2< 2010 Н/мм. Заключение По данным математического моделирования, в условиях нестабильного положения позвоночника, связанного с разрушением межпозвонкового диска или тела позвонка, в том числе с изменением его упруго-прочностных свойств или геометрических параметров, оптимальным вариантом его стабилизации является применение фиксирующих конструкций упругого типа (например транспедикулярных систем с пружинными штангами из NI-TI-сплава или системы «Dynesis»). Это позволяет сохранить распределение эпюр нагрузок на тела позвонков в пределах значений, близких к природным – 0,7 / 0,3 [3]. Выводы 1. При нестабильности позвоночника более физиологично применение 2. Применение динамических фиксирующих систем при межтеловой динамических фиксирующих систем. стабилизации является профилактикой раннего износа смежных дисков в системе [9].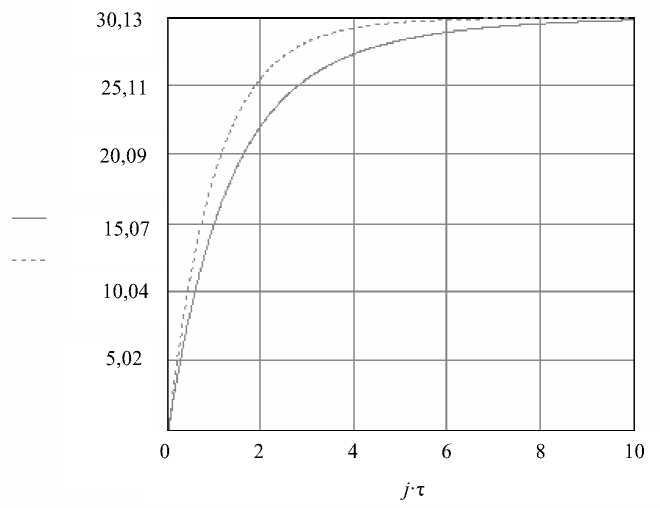
Список литературы Математическое моделирование нестабильности позвоночника и методов стабилизации
- Громов А.П. Биомеханика травмы. -М.: Медицина, 1979. -С.179-210.
- Давыдов Е.А., Загородний Н.В., Древаль О.Н. Основные направления разработки и использования конструкций с эффектом памяти формы для динамической стабилизации позвоночника//Современные технологии в травматологии и ортопедии: материалы III Междунар. конгр. -М., 2006. -С. 241.
- Орлов С.В., Бобарыкин Н.Д., Латышев К.С. Математическая модель стабильности трёхпозвонкового комплекса//Математическое моделирование. -2006. -Т. 18, № 10. -С. 55-70.
- Орлов С.В., Каныкин А.Ю., Москалёв В.П., Щедрёнок В.В., Седов Р.Л. Математический расчёт прочности позвоночного столба при хирургическом лечении нестабильных переломов позвоночника//Вестник хирургии имени И.И. Грекова. -2009. -Т. 168, № 2. -С. 61-64.
- Седов Р.Л., Орлов С.В., Бобарыкин Н.Д. О расчёте параметров динамических стабилизирующих конструкций на основе математической модели трёхпозвонкового комплекса человека//Математическое моделирование. -2010. -Т. 22, № 2. -С. 113-123.
- Denis F. Spinal instability as defined by the three column spine concept in acute spinal trauma//Clin. Orthop. -1984. -Vol. 189. -P. 65.
- Fergusson R., Tencer A., Woodard P., Allen A. Biomechanical comparison of spinal fracture models and the stabilizing effects of posterior instrumentations//Spine. -1988. -Vol. 13. -P. 453.
- Reno L. Surgery of the Spine. -Berlin-Heidelberg: Springer-Verlag, 1983. -P. 55-58.
- Haher T.R., Felmly W.T., O'Brien M. Thoracic and lumbar fractures: diagnosis and management//Spinal Surgery. -1991. -Vol. 2. -P. 857-910.
- Wagner U.A. Unter mitarbeit von Ottmar Schmitt, Hans-Martin Schmidt, Wallny T. Atlas der Pedikelschraubenimplantate. -Georg Thieme Verlag Stuttgart, 1998. -P.1-2.


