Математическое моделирование нестационарного теплопереноса в селективном лазерном плавлении на основе машинного обучения

3D-печать по технологии селективного лазерного плавления (СЛП) активно используется для производства сложных деталей в аэрокосмической промышленности [1]. Эта технология основана на послойном синтезе детали на основе её компьютерной модели путём сплавления лазером металлического порошка [2]. Физические процессы в СЛП включают комплекс термомеханических явлений, происходящих в различных пространственно-временных границах. Например, на уровне ванны расплава происходят процессы нагрева, плавления и испарения металла, а также теплопередачи путём теплопроводности, конвекции и излучения. В детали за счёт тепловых деформаций происходит накопление остаточных напряжений, что сказывается на итоговой форме напечатанного изделия. В данной работе рассматриваются вопросы математического моделирования процессов теплопередачи, происходящих в СЛП на макроуровне (на уровне детали) [3].

Тепловой расчёт процесса печати в трёхмерной постановке ввиду нестационарного характера и нелинейных эффектов в материале сопровождается значительными вычислитель- ными затратами. В частности, опыт использования программного комплекса Ansys Additive1 показывает, что время расчёта реальных изделий может измеряться сутками. Поэтому актуальной является проблема ускорения численного моделирования процесса 3D-печати.

Задача упрощается для расчётов однотипных изделий. В этом случае целесообразно обучить нейронную сеть (НС) и в последующем использовать её для быстрого определения температурного поля при различных комбинациях исходных параметров. НС в настоящее время используются в различных предметных областях: от генерации текста и мультимедиа контента [4, 5] до аппроксимации сложных математических моделей (ММ) физических систем [6].

НС и машинное обучение в области аддитивных технологий применяются следующим образом [7]: при проектировании изделий для 3 D -печати – это синтез материалов с заданными свойствами и проведение топологической оптимизации; при выборе параметров технологического процесса – оптимизация и мониторинг дефектов печати в реальном времени; при планировании аддитивного производства – для контроля качества готовых изделий.

Для оценки принципиальной возможности использования НС для приближённого описания процессов теплопередачи при 3 D -печати в данной работе рассматривается одномерная идеализация теплового процесса, когда учитывается только распространение тепла вдоль оси печати (оси Z). Использование такой модели представляется вполне оправданным в случаях, когда высота изделия значительно превышает два других габаритных размера. Одномерная идеализация при моделировании теплопереноса в аддитивном процессе использована в работе [8]. Решение нестационарной тепловой задачи оптимального управления технологическим процессом индукционного нагрева заготовки рассмотрено в работах [9, 10].

1 Математическая модель теплопередачи в процессе 3D-печати

В данной работе рассматривается ММ теплопередачи в процессе послойного синтеза в одномерной постановке, когда изменение температуры учитывается только в направлении оси печати Z . При этом геометрическая модель изготавливаемой конструкции может быть описана в виде стержня с изменяющимся вдоль оси Z поперечным сечением A = A ( z ) .

Количество теплоты Q , необходимое для нагрева массы m с некоторой температуры T _*

до температуры T, вычисляется по известной формуле: Q = cm (T - Т*), где с - удельная теп- лоёмкость материала. Для вычисления количества теплоты в единице объёма стержня необходимо продифференцировать обе части этого уравнения по объёму V:

dQ dV

р ( T - T . ) ,

где р = dm/dV - плотность материала. Тепловая мощность в единице объёма находится путём дифференцирования полученного соотношения по времени t , что с учётом независимости T _* от t приводит к формуле:

dQ_ дТ dV ~ СР dt где точкой над Q обозначена производная по времени. Тепловой поток q в стержне, по определению, представляет собой тепловую мощность, приходящуюся на единицу поперечного сечения: q = Q/A, откуда Q = q • A . Учёт того факта, что элемент объёма dV выражается через площадь сечения как dV = A • dz даёт

• ¹    Модуль для моделирования процессов 3 D -печати Ansys Additive . https://www.ansys.com/products/additive .

^{1 д} (   л\ ^Э T

- •—( q • A ) = cp— .

A d z           д t

Связь градиента температуры и теплового потока определяется законом Фурье:

, д T q = к дz где k - коэффициент теплопроводности. Подстановка этого выражения в предыдущую формулу в предположении постоянства k по координате z приводит к дифференциальному урав нению теплопроводности для стержня переменного сечения следующего вида:

д(„д T Л p cA д T

— I A 1 = д z v д z J k д t

Следует заметить, что при постоянной площади сечения величина A выносится из-под оператора дифференцирования по z и, после очевидного сокращения, формула (1) трансформируется в классическое одномерное уравнение нестационарной теплопроводности. Граничное условие (ГУ) на «подвижном» (наплавляемом) конце стержня соответствует поддержанию заданной максимальной температуры:

^{T (} z , t )| z = L ( t i ) = T ax - ⁽²⁾

ГУ на «неподвижном» конце стержня задаётся в виде уравнения конвекции:

h ( ^T ( z . t ) z = 0 ^- T ™ ) = ^k T

Здесь Tmin - температура окружающей среды, h - коэффициент конвективной теплоотдачи. При h > от данное ГУ трансформируется в условие поддержания постоянной Tmin на неподвижном конце стержня. Принимая для h конечные значения, можно обеспечить физически адекватное значение температуры на неподвижном конце стержня.

Уравнение теплопроводности (1) решается итерационно в цикле по временным шагам. На каждом шаге A t происходит увеличение длины стержня на величину A L . Длина стержня L увеличивается с течением времени, что соответствует пошаговому добавлению материала при 3Э-печати. Начальное распределение температур задаётся на основе поля температур на предыдущей итерации:

T ( z ■ t ) t = , i = ^T ( z , t )| , =_.

Для решения уравнений в частных производных в Matlab используется функция « pdepe ». Правила использования данной функции предполагают, что уравнение должно быть представлено в виде [11]:

( /тдtЛдt   -n c z, t, T ,           = z

V       д z J д t

£f n tr^L , ^z f I z , t , T , _я д z V    V      д z

д

д z

.  (    .^д T Л

+ s z , t , T ,       .

I       д z J

где функции c, f и s, а также коэффициент n задаются таким образом, чтобы уравнение (4) в точности соответствовало решаемой задаче. В данном случае для величин с, m,f, s получа- ются следующие значения:

(    д t Л pC p A Л^тт Ад t   _{n A}

с z , t , u ,       =         , f z , t , T ,       = A , s = 0, n = 0.

V       д z j k V       д z J     д z

Подстановка этих значений в уравнение (4) приводит к исходному уравнению (1). Общий вид выражения для ГУ в Matlab следующий:

(      д T Л

Pi ( z , t , T ) + q_t ( z , t ) • f | z , t , T ,       1 = 0, i = l , r .

V       д z J

Здесь функции p_i и q_i должны быть заданы для обоих концов стержня: условно левого (индекс l ) и условно правого (индекс r ) – неподвижного и подвижного концов стержня соответственно. Для реализации ГУ по обеспечению заданной температуры необходимо на подвижном конце стержня задать

P r ( z , t . T ) = T - T max , q r ( z >  t ) = 0.

где T – текущая температура стержня, T max – температура на подвижном конце стержня.

ГУ конвекции на неподвижном конце стержня задаётся как

P l ( Z , t , T ) = A plate h ( T in — T o ) ,

« I ( z . t ) = ^{- k} plate '

Здесь Aplate – площадь поперечного сечения плиты, kplate – коэффициент её теплопроводности, T0 – температура окружающего плиту пространства. Подстановка этих значений в (6), с учётом выражения для функции f в формуле (5), приводит к условиям (2) и (3) соответствен- но.

Зависимость площади сечения от координаты z задаётся функцией

A ( ^z )

A plate , ^Z — ^L plate , ^ A part ’ z >  ^L plate '

Здесь A _part – площадь поперечного сечения детали, L _plate – толщина опорной плиты.

В качестве тестовой задачи использован образец, представленный на рисунке 1, на котором показан процесс печати в текущей стадии, где итоговые очертания детали показаны пунктиром. Размеры на рисунке указаны в миллиметрах. Свойства материала соответствуют алюминиевому сплаву: ρ = 2700 кг/м 3 , с p = 900 Дж/(кг·К), k = 122 Вт/(м·К). Коэффициент теплоотдачи h принят равным 500 Вт/м 2 .

Б                 Вид Б

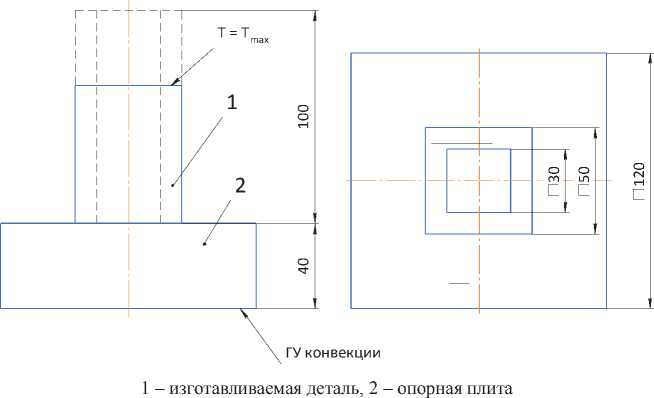
Рисунок 1 – Геометрия образца для тестовой задачи

Максимальная температура, поддерживаемая на верхнем конце детали, соответствует температуре плавления типового алюминиевого сплава и составляет 660 °C.

Распределение температуры в конечный момент времени, полученное в результате численного решения уравнения (1), приведено на рисунке 2. Из рисунка видно, что распределение температуры имеет кусочно-линейный характер. Это означает установившийся характер теплопередачи и позволяет построить квазистационарную аналитическую модель процесса. В последующем обучении НС, связанном с многократным расчётом температурного поля, это обстоятельство позволит значительно со-

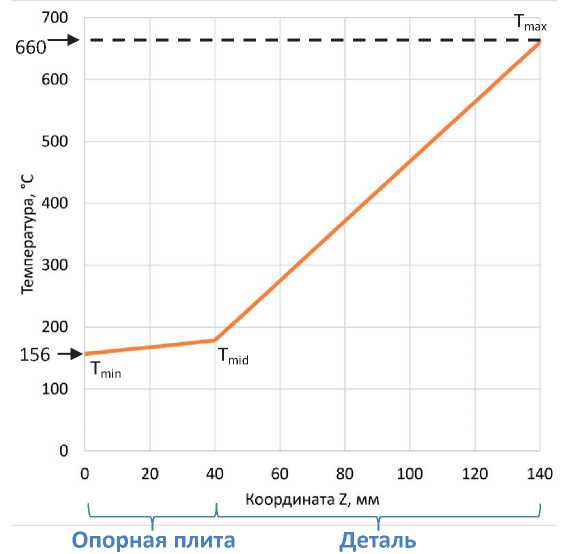
Рисунок 2 – Распределение температуры в конечный момент времени

кратить время обучения. Распреде-

ление температур можно с достаточной точностью описать функцией:

T ( z ) =!

T min

T .-T mid min

^Z , 0 - ^Z - ^Z plate z plate

T mid

+

T max

—

T mid

^Z part    ^Z plate

' ⁽ z   z plate )

z plate

где ^Z plate = L plate — ТОЛЩИНа ОПОрНОЙ ПЛИТЫ, L _part — ВЫСОТа детали, z part = L _pl ate + L part .

Для вычисления температуры на границе раздела «плита-деталь» Tmid и температуры в основании опорной плиты Tmin можно воспользоваться законом сохранения энергии:

q plate A plate = q part A part , q conv A plate     q plate A plate .

Первое уравнение отражает равенство количества тепловой энергии, уходящее в едини- цу времени с детали, количеству энергии в единицу времени, поглощаемую опорной плитой.

Второй уравнение отражает аналогичное равенство в отношении конвективного теплового потока и теплового потока с опорной плиты. Воспользовавшись далее законом Фурье, связы- вающим градиент температуры и тепловой поток [12], можно получить:

plate

L plate

T + min

A plate

\ L plate

+ AT

L part у

T mid

part max Lpart

(   k. Л      k.

h + .      T™ — /ate- T mid = hT o .

^      L plate у          L plate

В результате получается система двух линейных уравнений относительно T _mid и T _min . Ввиду громоздкости общего решения системы (8), в программном коде она решается численно методом Гаусса.

Таким образом, системы уравнений (7) и (8) определяют ММ теплового процесса, которая используется для обучения НС.

2    Модель теплопереноса в 3D-печати при помощи НС

Рассмотрена задача построения приближённого представления ММ, описанной в разделе 1, при помощи искусственной НС. В качестве параметров для обучения НС и получения распределения температуры T ( z ) исследованы четыре геометрических размера: площадь сечения плиты S plate и образца S part , их длины L plate и L part . Свойства материала и ГУ остаются неизменными. Таким образом, температура является функцией пяти аргументов: T = T ( z , S plate , L plate , S part , L part ) . Заданы следующие диапазоны изменения этих параметров: A min = ^0.5 Pi 0 , Р max = ^1.5 P_t 0 , где для краткости обозначено p = S _plate, S p _art, ^L _plate, L _part , а p ^ ^- некоторое начальное значение параметра. Диапазон изменения координаты определяется максимальными значениями длин плиты и детали: z _mln = 0, z m_K = L ^ m_K + ^L part max .

Для обучения НС необходимо в диапазоне изменения параметров сгенерировать обучающую выборку. Это набор комбинаций параметров и соответствующей им температуры, вычисленной при помощи ММ. Здесь можно воспользоваться планом эксперимента, например, таким как центральный композиционный план или план Бокса-Бенкена [13]. В данной работе использован подход, в котором количество точек в пространстве параметров ограничено заданным числом n tra n = 1000. Обучающая выборка строится следующим образом:

{ p } = rand ( p ^, P max , n_tmin ) , { z } = ^rand ( 0, ^z max , n_tmm ) , где «rand» – функция, формирующая массив случайных чисел размерности n tra n в заданном диапазоне. Построение обучающей выборки завершается вычислением температуры по формулам (7) и (8) для каждой комбинации параметров p и координаты z.

Важным фактором, влияющим на качество аппроксимации НС, являются абсолютные значения диапазонов изменения входных и выходных параметров. В качестве функции активации в НС часто используется гиперболический тангенс tanh ( x ), который принимает значения от -1 до 1 и является гладкой (дифференцируемой) аппроксимацией ступенчатой функции. Поэтому, если отобразить (отмасштабировать) все параметры на данный отрезок, то качество процесса обучения улучшится. В этом случае большинство значений внутри НС будут находиться на квазилинейном участке с tanh ( x ) и алгоритму обучения (часто используется градиентный спуск [14]) проще найти минимум функции потерь. Масштабирование уместно, когда параметры имеют различные физические размерности. В работе использовалось масштабирование всех параметров на отрезок [-1, 1] при помощи функции линейной интерполяции из библиотеки NumPy 2 .

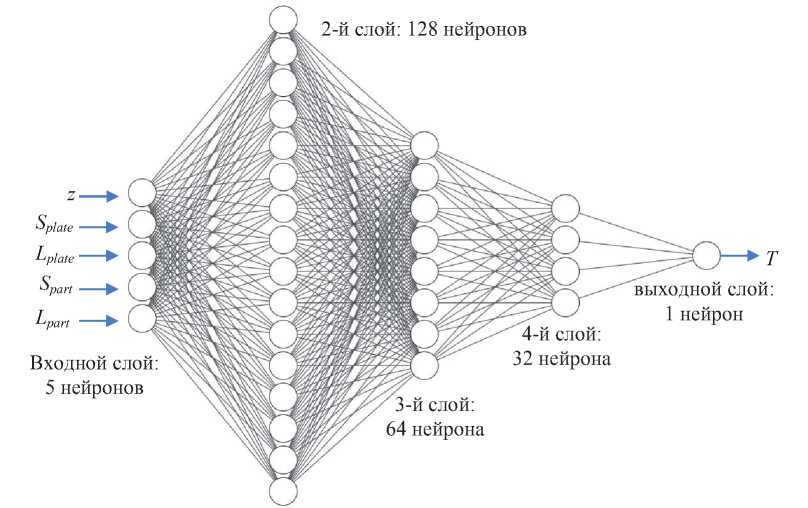
Архитектура НС показана на рисунке 3.

Программная реализация НС осуществлена на языке Python с использованием библиотеки TensorFlow 3 . Архитектура НС определена на основе примеров из документации к данной библиотеке. В качестве функции активации для всех слоёв использован tanh ( x ). Для обучения НС использован алгоритм оптимизации Adam [15]. Максимальное количество «эпох» –

• ²    Библиотека численных методов NumPy для языка Python . https://numpy.org/doc/stable/reference/generated/numpy.interp.html .

• ³    Библиотека Tensor-Flow ( https://www.tensorflow.org/ ) для языка Python .

просмотров обучающей выборки – равно 100. Тестовые расчёты показывают, что данный параметр в совокупности с типом функции активации и методом оптимизации оказывают наиболее существенное влияние на точность нейросетевой аппроксимации. В качестве функции потерь принято среднеквадратичное отклонение. Для ускорения обращения к обученной НС реализовано сохранение архитектуры сети и её весов в иерархическом формате данных ( HDF5 ) с последующим импортом перед использованием.

S plate L plate part L part

2-й слой: 128 нейронов

Входной слой: 5 нейронов

T

3-й слой:

64 нейрона

4-й слой:

32 нейрона выходной слой: 1 нейрон

Рисунок 3 – Архитектура используемой нейронной сети

3 Использование НС для определения температур в образце Рисунок 4 – Распределение температур

С использованием обученной НС построено распределение температур в конечный момент времени в изготовленном образце. Набор входных параметров определён следующим образом. Задано количество тестовых точек (комбинаций значений параметров) n test =50. Определены векторы входных параметров {p i } размерности n test и постоянные значения p i0 , например,    L pae 0 = 0,04 м,    ^L_par_t 0 = 0,1 м,

S pate 0 = 0,0144 м, S part 0 = ^0,0016 м. Вектор координат {z} заполняется арифметической прогрессией от ⁰ до ^Lp_la_te 0 + L part 0 . Полученный набор значений формирует тестовую выборку, которая нормируется на отрезке [-1,1] и подаётся на вход НС. Вычисляются температуры по заданным входным параметрам. Полученный на выходе вектор температур приводится к исходному масштабу, поскольку на этапе обучения он подвергался нормированию.

Результаты расчёта температур в образце с       по математической модели и нейросети использованием НС приведены на рисунке 4.

Выводы

Сопоставляя распределения температур по высоте плиты и детали, полученные с использованием ММ и НС (рисунок 4), можно сделать вывод, что НС обеспечивает достаточно высокую точность. Этот результат показывает принципиальную возможность нейросетевой аппроксимации ММ физических систем, поведение которых описывается дифференциальными уравнениями в частных производных. Деталь, выращиваемая на 3 D -принтере, в совокупности с процессами теплопереноса, относится к таким системам.