Математическое моделирование операций финишной обработки

где y – обобщенный критерий качества технологического процесса (производительность, экономическая эффективность, качество изделия и т.д.);

x_i – технологические факторы (режимы обработки, свойства обрабатываемого материала, характеристики инструмента, свойства технологической среды и т.д.);

a_i, b-_i – коэффициенты, характеризующие зависимость качества поверхности от i- го технологического фактора.

Комплексные исследования, выполненные в отношении обеспечения эффективности финишных операций обработки авиационных деталей, позволили установить характер и степень влияния свойств технологических сред на результаты процесса при полировании заготовок эластичными кругами.

В результате получены зависимости, характеризующие физические показатели процесса полирования:

P = 46,826–5,5х1+9,324х2+4,6х3+6,328х4+0,12х12+ y +1,7х13–7,06х14+12,14х23+4,423х24 ;

Pz =30,413-12,713х1+8,12х2+13,624х3+15,4х4+

+2,8х12–3,824х13–10,8х14+15,6х23+6,4х24;

Тк =147,73-62х1+10,2х2+43,2х3+47,5х4+12,25х12– –24,17х13–40,2х14+36,8х23–7,2х24, (2)

где x_i,…,x_ij – факторы, определяющие условия обработки.

Анализ приведенных соотношений показал, что наибольшее влияние на механизм взаимодействия контактирующих поверхностей при резании оказывают радиальная деформация круга, физико-механические свойства материала, характеристика эластичного инструмента, физико-химические свойства технологической среды.

Установлено, что степень влияния технологической среды значительно выше, чем воздействие остальных факторов. В результате целенаправленного формирования свойств среды возможно эффективное управление температурно-силовой напряженностью процесса резания, что определяет значения выходных показателей качества получаемых изделий.

Шероховатость поверхностей авиационных деталей оказывает непосредственное влияние на такие эксплуатационные характеристики, как трение, износ, теплопроводность и контактная жесткость. Влияние технологической среды на микрогеометрию поверхности, полированной эластичными кругами, осуществлялось в отношении среднеарифметического отклонения профиля на базовой длине. Установлены следующие математические зависимости параметра R_a от времени полирования, как у = 6(х).

Для обработки без импрегнатора:

y = 9,89*10-15*х8-4,68*10-12*х7+8,98*10-10*х6– 9,05*10-8*х5+5,08*10-6*х4+1,55*10-4*х3+

+2,34*10-3*х2-2,27*10-2*х+1,22;               (3)

для обработки с высоковязким импрегнатором: y = 1,14*10-15*х8-1,11*10-12*х7+3,49*10-10*х6– –5,18*10-8*х5+4,14*10-6*х4–1,83*10-4*х3+ +4,49*10-3*х2-6,74*10-2*х+1,26,               (4)

где y – параметр R_a шероховатости поверхности, мкм;

x – время полирования, с.

Установлено, что лучшие результаты как по величине R_a , так и по времени ее достижения обеспечивают составы технологической среды, достаточно эффективные по съему материала заготовки. Также выявлено, что значения R_a имеют разброс на разных участках поверхности, причем тем больший, чем меньше эффективность используемого состава технологической среды.

Моделировать поверхность обычно начинают с отдельного выступа. Выбор модели выступа – первый шаг при исследовании закономерностей функционирования поверхностей (трения, изнашивания, деформирования и т.д.). Согласно общим принципам моделирования выбранная модель должна наиболее близко характеризовать геометрические параметры отдельных выступов и отражать процесс взаимодействия моделируемой поверхности с другими.

Различают моделирование двух видов – нормальное к поверхности и касательное к поверхности.

Моделирование нормальной моделью эффективно отражает геометрические характеристики выступов в условиях, когда поперечная и продольная шероховатости соизмеримы. При несоизмеримых шероховатостях хорошо отражает геометрические характеристики выступов касательная модель.

Каждая из упомянутых моделей имеет свою, ей присущую геометрическую характеристику.

Например, для “стержневой” модели (нормальная цилиндрическая модель) характерным геометрическим параметром является площадь или диаметр основания модели, для сферической модели таким параметром служит радиус кривизны вершины модели, для конической – угол конусности и т.п.

При моделировании необходимо также учитывать условия, в которых в дальнейшем будет работать моделируемая поверхность. Размер и форма неровностей профиля могут в большей или меньшей степени меняться в пределах одной поверхности. Соответственно различают три типа профилей: детерминированный, случайный и смешанный. Критерием оценки типа профиля является корреляционная функция.

Для детерминированного профиля корреляционная функция имеет сходство с самим профилем. Корреляционная функция профилей со случайным характером неровностей (профиль поверхностей после обработки абразивными инструментами) быстро убывает, монотонно или образуя затухающие колебания. Корреляционная функция смешанного профиля зависит от его структуры и определяется сочетанием корреляционных функций детерминированных и случайных профилей.

Задавать модель профиля следует высотными и шаговыми параметрами, причем соответствие стандартных характеристик реального профиля его модели может быть принято за критерий правильности ее выбора. Наиболее целесообразно в этом случае задавать модель стандартными параметрами (в соответствии с ГОСТ 7016-82): Rz , Ra , Sz . Однако данных усредненных характеристик профиля недостаточно для задания модели, поскольку они не учитывают, например, углов раскрытия впадин неровностей, размеров площадок при вершинах, а также высот и шагов отдельных неровностей.

В общем случае для моделирования профиля выступами в виде трапеций и впадинами треугольной формы необходимо знать текущие координаты: x₁, x₂, x₃, x₄, y₁, y₂, y₃, y₄ (рис. 1), т.е. при допущении равенства y₂ = y₃ надо знать 7 параметров. Задание модели профиля угловыми параметрами несколько усложняет ее описание, хотя в конечном счете сводится к названным 7 параметрам. Менее сложными с точки зрения их получения оказываются следующие параметры:

h ⁺ – отклонение вершины выступа, достроенного до треугольной формы, от средней линии;

й – отклонение вершины реального выступа от средней линии;

h ^- – отклонение дна впадины от средней линии;

h – высота достроенной неровности;

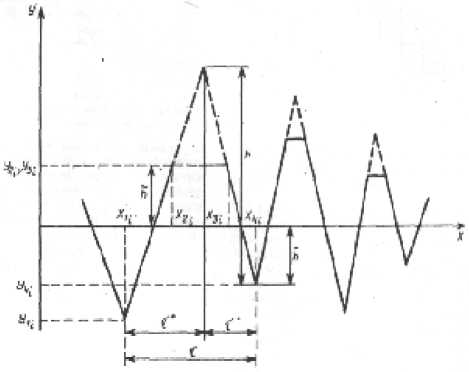
Рис. 1. Модель неровностей профиля и ее характеристики

т ,т - составляющие шага т неровности по впадинам.

Для успешной реализации модели необходимо иметь не только названные параметры, но и сведения о взаимосвязи и законах их распределения. Наличие или отсутствие связи между параметрами может характеризоваться величиной коэффициента корреляции.

Величины коэффициентов корреляции позволяют сделать вывод о наличии связи между параметрами τ ⁺ и τ , τ ^- и τ , h⁺ и h, h^- и h . Вместе с тем малые коэффициенты корреляции между параметрами h⁺ и й свидетельствуют о независимости Л . Уравнения взаимосвязи параметров:

для шаговых параметров:

Т + = |т(1 + е),(5)

т ^т(1  s),(6)

где ε – относительная ошибка, характеризующая разброс параметров от прямой;

для высотных параметров:

V = hk - 5,(7)

h~ = h(l — к) + 5,(8)

где k – коэффициент, характеризующий угол наклона прямой;

δ – постоянный коэффициент для данного профиля.

Законы распределения шаговых параметров изучают следующим образом. Строят гистограммы распределения параметров τ и ε ; выдвигают гипотезы о законах распределения этих параметров, принимая во внимание соотношения (5) и (6), а также закон распределения τ и ε (в соответствии с выдвинутыми гипотезами), рассчитывают значения τ ⁺ и τ ^- с разбивкой по классам; строят экспериментальные и теоретические гистограммы для τ ⁺ и τ ^-; по критерию c² проверяют соответствие теоретических данных экспериментальным.

Характер гистограмм показывает, что для этих параметров можно принять в качестве рабочих гипотез логарифмически нормальное ( τ ) и нормальное ( χ ) распределения. Логарифмически нормальное распределение характеризуется параметрами s² и b , определяемыми по формулам:

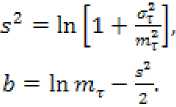
Плотность распределения имеет вид:

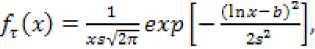
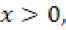
где СГ - дисперсия параметра τ ;

m_ф – математическое ожидание параметра τ .

Характеристика нормального распределения включает параметры m_е и сг_² . Анализ экспериментальных данных свидетельствует о малости математического ожидания m_е , поэтому значение его можно принять равным нулю, т.е. m_е = 0 .

На основании уравнения (5) взаимосвязи шаговых параметров получена формула (12) для определения дисперсии параметра ε :

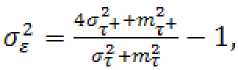
где m, m_T+ – математические ожидания соответственно параметров τ и τ ⁺ ;

а^ , ^Л – дисперсии соответствующих параметров ф и ф⁺ .

Правильность выдвигаемых гипотез о распределении шага неровностей и параметра е проверим по критерию χ2, определенному для параметров τ+ и τ-. Рассчитанные с использо- ванием теоретических и экспериментальных данных значения критериев c2 не превышают соответствующих значенийχ2 при 1%-ном уровне значимости. Это обстоятельство позволяет принять выдвинутые гипотезы о законах распре- деления шаговых параметров и их взаимосвязи.

Взаимосвязь высотных параметров определяется уравнениями (7) и (8). Теоретическими расчетами получены формулы для характеристики входящих в уравнения (7) и (8) коэффициентов: а = тп_нтп_к = m_h+,        (13)

^

ffh+”ahmk

где Tn_h,m_k,Tn_h+ – математические ожидания параметров h, k, h⁺ соответственно;

^h , ^k , C"k + – дисперсии параметров h, k, h+ соответственно;

cov(ft⁺, h) – ковариация параметров h ⁺ ,h.

Законы распределения высотных параметров изучим так же, как и шаговых. Характер гистог- раммы показывает, что для этого параметра можно принять логарифмически нормальное распределение с показателями 5^ и bh, причем:

и плотность распределения fh. (X) будет иметь вид:

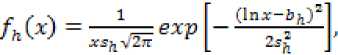
x > 0

Для параметра k может быть принят нормальный закон распределения с характеристиками m_k и OV, определенными по формулам (15), (16).

Проверка соответствия закона распределения параметра h логарифмически нормальному дала положительные результаты.

Для высотных параметров правильность выдвигаемых гипотез о законах распределения проверяют по критерию χ2, определенному для параметров h+ и h- .

Значения критериев χ ² , полученные расчетным путем, не превышают соответствующих значений при 1%-ном уровне значимости. Это обстоятельство позволяет принять выдвинутые гипотезы о законах распределения высотных параметров и их взаимосвязи.

Характер гистограммы распределения (независимого от других) высотного параметра Й дает возможность принять в качестве рабочей гипотезы нормальный закон распределения. Проверка по критерию χ ² подтвердила правильность выдвинутой гипотезы.

Таким образом, построена математическая модель шероховатой поверхности, окончательную проверку которой можно выполнить по стандартным характеристикам профиля, т.е. по параметрам R_z и R_a . Сопоставление результатов расчета по программе R_z и R_a с экспериментальными значениями этих параметров подтвердило правильность выбора модели и ее характеристик.

MATHEMATICAL MODELLING OF OPERATIONS OF FINISHING PROCESSING

Павел Дубровский, Candidate of Technics, Associate Professor at the Aircraft Construction Department.

Inna Lukina, Graduate Student.

Никита Дубровский, Software Engineer UlSTU