Математическое моделирование оптоакустического сигнала от агрегированных эритроцитов для оценки уровня агрегации

Рассмотрим воздействие лазерного излучения Nd: YAG с длиной волны 1064 нм на математическую модель агрегированных эритроцитов при фиксированном гематокрите. Ранее в [1–4] была разработана модель формирования отклика оптоакустического сигнала от одиночного эритроцита и была смоделирована математическая модель формирования оптоакустического сигнала (ОАС) в результате воздействия лазерного излучения на модельные образцы крови с учетом изменения гематокрита. Было отмечено, что уровень ОА сигнала монотонно возрастал по мере увеличения концентрации эритроцитов. Амплитуда спектральной плотности мощности ОАС возрастала с увеличением количества источников формирования оптоакустического сигнала, что позволяет определять уровень гематокрита. В этой работе рассмотрим формирование ОАС от агрегированных эритроцитов, разработаем метод упаковки эритроцитов в кластеры различного размера и при различных уровнях агрегации.

Агрегация эритроцитов (АЭ) может служить диагностическим параметром для патологических состояний. При патологиях может возникать так называемый "гиперагрегационный синдром", при котором эритроциты аномально быстро и прочно агрегируют. Изменение АЭ при патологиях связывают в основном с изменением концентрации белков плазмы крови и в меньшей степени с изменением свойств самих эритроцитов.

Конфигурация кровяных тканей агрегированных эритроцитов может быть получена различны- ми путями. Например, в [5] эмпирически моделировали энергию взаимодействия клеточных пар как комбинацию стерического и притягивающего потенциалов, а затем применяли технику Монте-Карло для развития системы в течение большого количества итераций для получения двумерных распределений агрегированных эритроцитов. При случайной свободной упаковке в двух измерениях можно обеспечить плотность упаковки ячеек 54– 55 %, тогда как в трех измерениях она составляет около 60 %. Таким образом, эти методы не способны обеспечить компактные кластеры. Однако для создания плотно упакованных кластеров эритроцитов можно использовать обычные схемы упаковки. Например, в двух измерениях плотность упаковки кругов (сфер) почти 90 % может быть достигнута с помощью схемы гексагональной упаковки. Эту схему упаковки можно использовать для организации окружностей, представляющих эритроциты, для образования агрегат. Сформированный кластер помещали случайным образом для создания агрегированного образца крови и многократно повторяли вычисления для различных образцов ткани. Следует отметить, что это — очень быстрый метод, потому что ячейки размещаются в фиксированных местоположениях в агрегате, а также способны формировать компактные кластеры.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Волновое уравнение для давления, создаваемого при поглощении оптического лазерного излучения при условии термоизоляции, можно запи- сать в виде [6, 7]:

V2 p -

1 d ² p v 1 d tt

в d H C p d t ’

где β — коэффициент изобарного теплового расширения, С p — теплоемкость, ν s — скорость звука в области действия лазера, H — тепловая энергия.

Пусть оптическое излучение интенсивности I 0 распространяется вдоль оси x , тогда функция нагрева H ( x , t ) = μI 0 e^–ωt . Здесь μ — коэффициент оптического поглощения освещенной среды, ω — частота модуляции оптического луча.

Можно получить аналитические решения уравнения (1) для некоторых простых форм (цилиндра, сферы и т. д.) при использовании соответствующих граничных условий [1, 3, 4, 6]. Давление оптикоакустического сигнала для равномерно освещенного сферического поглотителя на расстоянии r можно найти как [1, 7, 8]

P \ ( ¹ ) =

i ωµβI ₀ ν _s α c p ( r / a )

x

[ л             л! i k ( (r -a )

sin 1 - 1 cos 1 ] e f

q ²

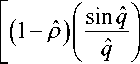
- cos 1 + i pv sin 1

где безразмерная частота определяется как q ˆ = ωα / ν s , α — радиус поглощающей сферы, k f — волновое число в жидкой среде для волны давления с частотой ω и определяется выражением k f = = ω / ν f . Аналогично, безразмерные величины ρ ˆ = = ρ s / ρ f и v ˆ = ν s / ν f представляют собой отношения плотности и скорости звука соответственно. Нижние индексы s и f используются для обозначения свойств поглотителя и окружающей жидкой среды соответственно, верхний индекс 1 в уравнении (2) означает, что рассматривается только один источник ОАС.

Предположим, что сферические поглотители освещались лазерным излучением с постоянной интенсивностью независимо от их пространственного положения и все многократные рассеяния светового пучка можно считать пренебрежимо малыми, а также ультразвуковые волны, генерируемые светопоглощающими сферическими частицами, не взаимодействуют друг с другом. При этих предположениях поле давления ОАС, создаваемое совокупностью поглощающих сфер, можно записать в виде линейной суперпозиции сферических волн, испускаемых отдельными источниками, поле давления от времени принимает вид

p } ^{( T )}

∞

xJ d1 ]

-^

i^eFv s ² _x 2nC_p ( r / a )

sin 1 - 1 cos 1 ]

1 (1 - p))

sin 1 ]       „           „

----I- cos 1 + ipv sin 1

1 )

-4- x

Суммарный член в приведенном выше уравнении учитывает интерференцию волн давления, генерируемых сферическими источниками, распределенными в пространстве. При этом r n — вектор положения n -й частицы и содержит N источников ОАС. Здесь k f определяет направление наблюдения [7].

МЕТОД УПАКОВКИ ЭРИТРОЦИТОВ

Зададимся размерами агрегируемого кластера и фиксированной величиной гематокрита. Модельные исследования будем проводить для образцов крови при 40 %-м гематокрите и при различных условиях кластеризации, или агрегации, и исследуем полученный ОА сигнал. Уровень гематокрита выбран 40 %, потому что он близок к нормальному уровню гематокрита 45 % в нормальной крови человека. [9]

Следующий шаг заключался в том, чтобы найти пространственные положения случайно распределенных, хорошо разделенных изотропных кластеров одинакового размера в пределах размеров образца ткани в периодических граничных условиях с использованием того же алгоритма. Количество кластеров также фиксировало число ячеек, которые могли быть присоединены к одному кластеру. Количество ячеек на кластер определялось делением общего количества ячеек на количество кластеров и усечением этого численного значения до ближайшего меньшего целочисленного значения. Это количество ячеек было позиционировано с использованием гексагональной упаковки для каждого кластера.

После этого были выбраны координаты центра круга, расположенного в центральной области этой прямоугольной области. Координаты центров других кругов регистрировались в соответствии с их расстояниями относительно этой контрольной точки для формирования таблицы поиска. Следующим шагом было взять координаты требуемо-

го количества кругов, прикрепленных к кластеру, из этой таблицы поиска и поместить их относительно центра кластера. В таблице поиска были указаны координаты окружностей относительно центра кластера. Для вычисления же уравнения (3) необходимы координаты этих окружностей относительно начала кластера, и это легко получить, суммируя координаты этих кругов (доступные из таблицы) и центра кластера. Точно так же координаты окружностей, связанных с другими кластерами, были взяты из справочной таблицы, и они были преобразованы в систему координат кластеров. Круги, не принадлежащие какому-либо кластеру, были размещены в пределах образца при неперекрывающихся условиях с другими кругами. Таким образом, были получены пространственные распределения неперекрывающихся, изотропных и идентичных кластеров, содержащих неперекры-вающиеся ячейки. Кроме того, для каждого агрегирующего условия был рассчитан средний радиус вращения кластеров для количественного определения среднего размера кластера. Радиус вращения кластера R_g определяли, используя квадрат расстояний ячеек от центра кластера. Численные значения R_g были получены для всех кластеров, связанных с реализацией ткани, и среднее значение было вычислено впоследствии. Неагрегиро-ванные эритроциты не рассматривались для оценки среднего радиуса агрегации кластеров.

Среднее число частиц, связанных с кластером, лежало в диапазоне от 7 до 61 и очень мало эритроцитов (< 4 %) ячеек не были частью агрегатов. Минимальное значение среднего радиуса вращения кластеров оценивалось в 5.51 мкм, а наивысшего агрегата — 16.06 мкм.

МОДЕЛИРОВАНИЕ

Предполагалось, что клетки были в сходных биофизических и биохимических условиях, которые в свою очередь позволили считать числовые значения физических параметров ( β , С_p и µ ) одинаковыми для всех ячеек, поэтому эти параметры ( β , С_p , µ и F ) считались константами [8].

Эритроциты находились в интересующей области 100 × 100 мкм для создания условия агрегации при моделировании реализаций двумерной ткани. Для каждого испытания было смоделировано 200 случаев ткани, представляющих возможные конфигурации тканей, и вычислены с помощью уравнения (3). Интеграл в (3) в каждой временнόй точке оценивали численно с использованием метода трапеций, и рассчитанное давление ОАС было комплексным количеством. Кривая ОАС была получена из реальных частей данных временнόго ряда давления ОАС, а огибающая сигнала была определена из соответствующих величин.

В Приложении на рис. 1–3 представлена пространственная расчетная модель структур из сферических отражателей (эритроцитов), порождающих оптоакустический сигнал при облучении лазером Nd: YAG [10–13]. Модель была простроена и рассчитана в программе Matlab.

ЗАКЛЮЧЕНИЕ

Представленная модель использовалась для изучения того, как амплитуда ОА сигнала и спектр мощности будут изменяться в зависимости от уровня агрегации эритроцитов. Было отмечено, что амплитуда ОА сигнала возрастает с увеличением уровня агрегации и уменьшается частота сигнала с увеличением размеров агрегата. Рассчитанная модель позволяет сделать вывод о возможности регистрации уровня агрегации эритроцитов в крови с помощью оптоакустического эффекта, возникающего в результате воздействия лазерного излучения с длинной волны 1064 нм на модельные образцы клеток. Тем не менее в разработанной модели пока не учитывался ряд факторов, таких как эффекты потока, ширина полосы ультразвукового приемного преобразователя и т. д., которые могут влиять на чувствительность предлагаемой модели. После уточнения всех этих факторов модель может быть скорректирована для измерения уровней агрегации эритроцитов, связанных с широким спектром патологий. Полученные результаты дополняют математическую модель рассчитанную ранее в [3, 13, 14] для неагрегированных эритроцитов.

ПРИЛОЖЕНИЕ

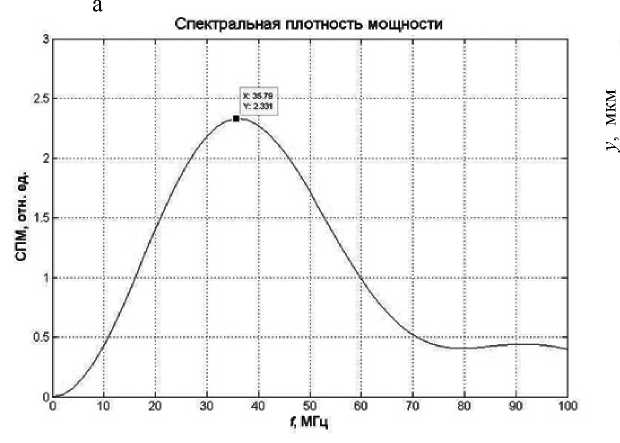
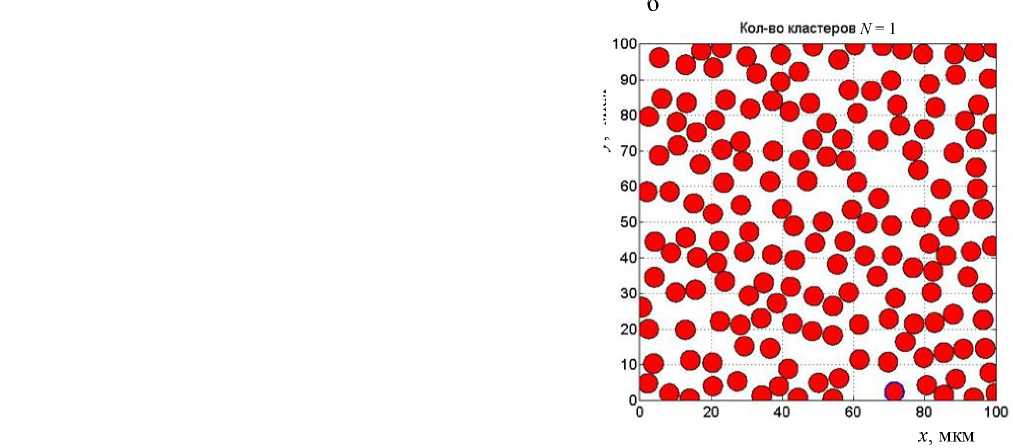
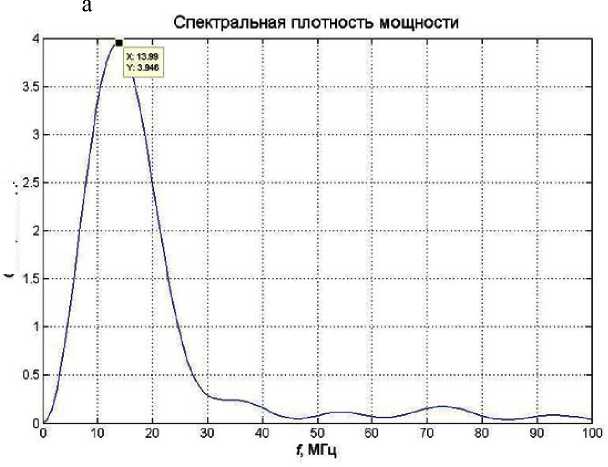
Рис. 1. Спектральная плотность мощности ОАС неагрегированных эритроцитов (а) и двумерная реализация образца ткани (б).

Количество неагрегированных эритроцитов 168

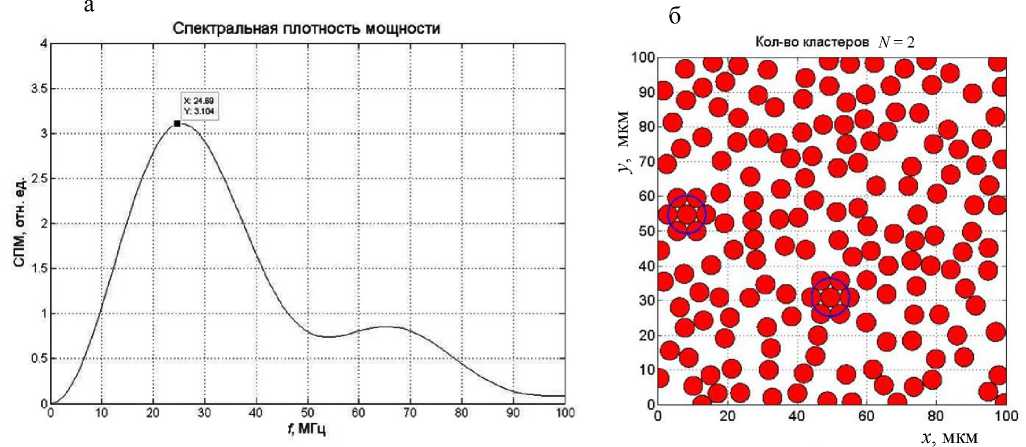
Рис. 2. Спектральная плотность мощности ОАС агрегированных эритроцитов (а) и двумерная реализация образца ткани (б).

Количество эритроцитов в кластере N = 7, радиус агрегата R g = 5.51 мкм. Неагрегированных эритроцитов 154. Процент агрегации 8.3 %

СПМ, отн. ед.

90 § И 80

^70

б

Кол-во кластеров N = 2

x , мкм

Рис. 3. Спектральная плотность мощности ОАС агрегированных эритроцитов (а) и двумерная реализация образца ткани (б).

Количество эритроцитов в кластере N = 61, радиус агрегата R g = 16.06 мкм. Неагрегированных эритроцитов 47. Процент агрегации 73 %