Математическое моделирование основных этапов технологического процесса механической обработки керамических и ферритовых деталей СВЧ- и КВЧ-устройств

В современной радиоэлектронике широко используются СВ× и КВ× функциональные узлы на основе керамических и ферритовых материалов [1; 2]. Ýто коаксиальные и диэлектрические резонаторы, полосно-пропускающие фильтры, ферритовые циркуляторы, вентили, переключатели и т. п. [3; 4].

Основным способом серийного изготовления заготовок из керамических материалов является прессование в пресс-формах с последующим обжигом.

Для производства ограниченного количества деталей, необходимого при проведении НИОКР, как правило, целесообразно использовать технологии, основанные на методах механической обработки серийно выпускаемых керамических заготовок [5]. Микроволновая керамика и ферриты по механическим свойствам представляют собой твердые и хрупкие материалы [6], механическая обработка которых (резка, шлифование, полирование, формирование отверстий) возможна, в основном, с использованием абразивных инструментов.

Целью совместных усилий разработчиков, конструкторов и технологов предприятий, разрабатывающих и выпускающих керамические и ферритовые СВ× и КВ× функциональные узлы, является повышение качества создаваемых устройств, улучшение их технических харак- теристик: сокращение затрат на их разработку и изготовление. Достижение поставленной цели возможно по двум направлениям: во-первых, за счет совершенствования методов проектирования; во-вторых, за счет создания и внедрения более совершенных технологий изготовления перечисленных устройств. В настоящее время возможности совершенствования методов проектирования в существенной степени исчерпаны. В области разработки более совершенных технологических процессов неиспользованных возможностей еще достаточно много. Причем они связаны не только с разработкой принципиально новых технологических процессов, но и с оптимизацией основных операций существующих технологических процессов на основе методов математического моделирования. При этом становится возможным оптимальный выбор технологического процесса, необходимого для данного вида механической обработки деталей с заданной степенью точности, без его предварительной реализации. В этом случае в качестве исходных требований по точности и качеству обработки используются результаты построения математических моделей функциональных СВ×- и КВ×-узлов.

В настоящей работе предложены математические модели основных операций технологического процесса механической обработки керамических и ферритовых заготовок, практическое использование которых позволяет оценивать

Рис. 1. Размещение зерен на поверхности абразивного круга

ожидаемую шероховатость поверхностей керамических и ферритовых деталей еще до этапа изготовления экспериментальных образцов.

Рассмотрено математическое моделирование основных этапов технологического процесса механической обработки керамических и ферритовых заготовок для формирования внешней поверхности (грубое шлифование абразивными кругами), а также моделирование формирования отверстий при сверлении заготовок алмазными сверлами. На основе результатов моделирования данных технологических операций оценивается пригодность полученного образца (детали СВ×-или КВ×-устройства) для следующей технологической операции, например, металлизации поверхностей, или необходима его дальнейшая механическая доработка (например, тонкое шлифование) с целью снижения шероховатости поверхностей, непосредственно влияющей на основные параметры устройства (например, добротность керамического резонатора [7]).

1. Математическое моделирование шлифования внешней поверхности керамических и ферритовых заготовок

Математическая модель техпроцесса обработки внешней поверхности заготовки шлифовальным кругом разрабатывалась с использованием схемы образования стружки по И.М. Брозголю [8]. В модель закладывались параметры зерен абразивного материала шлифовального круга, форма которых аппроксимирована эллипсом, а также осевой люфт. Распределение зерен по углу наклона а полуосей аппроксимирующего зерно эллипса на поверхности абразивного круга – случайное, равновероятное.

Процесс возникновения неровностей вследствие геометрических причин принято трактовать как копирование на обрабатываемой поверхности траектории движения и формы режущих кромок зерен. С геометрической точки зрения величина, форма и взаимное расположение не- ровностей (направление обработочных канавок) определяются формой и состоянием режущих кромок зерен и теми элементами режима резания, которые влияют на изменение траектории движения режущих кромок зерен относительно обрабатываемой поверхности [9].

Причинами осевого люфта является ряд факторов, имеющих разную природу: деформация и микроскалывание материала, наличие люфтов в механизмах обрабатывающего оборудования и др. [10].

Модель абразивного круга построена на основе функциональной зависимости положения режущих кромок зерен на его поверхности. Размещение зерен на поверхности абразивного круга схематично показано на рис. 1.

Общее уравнение эллипса, аппроксимирующего абразивное зерно, имеет вид

(X cos а + Y sin а ) ² + a ²

(Y cos а - X sin а ) ²

⁺------ b2-------

= 1,

где а — угол поворота; а и b — полуоси эллипса.

После решения уравнения (1) относительно переменных X и Y получим

Y 1,2 =

- BX ± V b ² X ² - 4 A ( CX ² - D )

2 A

0 _ - BY ± У B ² Y ² - 4 C ( AY ² - D ) Хд 9 =---------------~-------------

1,2

с учетом сдвигов по осям OХ и OY

Y 1,2 = [ - B ( X - x ₀) ±

Рис. 2. Вид профиля поверхности после шлифования

Рис. 3. Вид профиля поверхности после тонкого шлифования

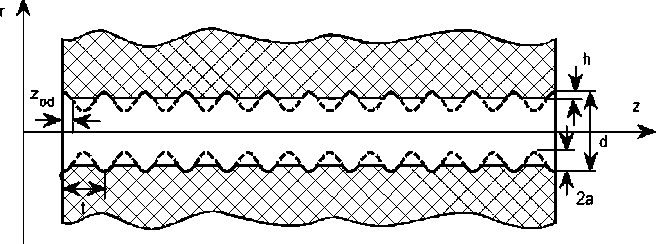
Рис. 4. Вид профиля поверхности отверстия после сверления алмазным сверлом (штриховая линия) и тонкого шлифования (сплошная линия)

D = a b ;

x ₀ – сдвиг по оси OX; y ₀ – сдвиг по оси OY.

Наличие осевого люфта õ_ë приводит к расширению канавок на поверхности обрабатываемой заготовки, образованных острыми кромками зерен круга. Таким образом, в результате первичной обработки заготовки периферией абразивного круга, с учетом осевого люфта, уравнение профиля шероховатой поверхности примет вид (для удобства X рассматривается как функция Y )

G_x = B ²( a n )( Y — У о n )² —

— 4 C ( a n )[ A ( a n )( Y — y o n )² — D ( a n )];

a n — случайное число в интервале 0 < a n < п ,

с равномерным распределением вероятности;

У о n = Y 2 ⁰( X min Y 2 n ) — сдвиг по оси OY n -го эл-

липса, x _{min Y 2 n} определяется из условия

— ( Y ° ⁰) = 0 и dX ²

x min Y 2 n

( — 1) m

X =

2 C ( a n )

⁺ x о n при

B ²( a n ) D ( a n )

\ [4 A ( a n ) C ( a n ) — B ²( a n )] C ( a n )’

⁽П = 1)     0 <  Y <  ^y01 + y min X 21

( n >  1) 0 <  Y <  y (n - 1) ё , n = 1,2... N ;

< F X ⁺ GXx 2 C ( a n )

^{+ X} 0 n

^{+ х}ё

при

0 <  Y <  y™ ,    n = 1,2... N ;

x min Y 2 n ⁺ x 0 n <  X <

< x min Y 2 n ^{+ X} 0 n ^{+ Х}ё ,

n = 1,2... N при Y = 0,

где F X = - B ( a _n )( Y — y o _n ); N — количество зерен на поверхности круга;

где f1

m =

при л/ 2 < a _n < п , при 0 < a _n < п/ 2;

X01 = X0(ymin X21) - сдвиг по оси OX 1-го эл липса, ymin X21 определяется из условия

— (Xo0) = 0 и dY 2

y min X 2 n

B ²( a n ) D ( a n )

\ [4 A ( a n ) C ( a n ) — B ²( a n )] A ( a n )’

где

m=

| 2

при п/ 2 < a _n < п , при 0 < a _n < п/ 2;

x о _n (для n >  1) — сдвиг по оси OX n -го эллипса, определяется из условия, что уравнение X 1 ( a n - 1 ) = X 2 ( a n ) имеет один действительный корень y n - 1 , x n - 1 = X 1 ( y n - 1 ), ⁽ x n - 1 , y n - 1 ) ^- координаты точки касания двух соседних ( n - 1) -го и n -го эллипсов; y_në – меньший корень уравнения X 1⁽ a n ) + ^хё = X 2^{( a} n + 1 ).

Вид профиля поверхности после шлифования схематично показан на рис. 2.

При необходимости уменьшения глубины канавок после грубого шлифования в технологический маршрут включается тонкое шлифование, осуществляемое алмазными кругами. В результате удается снизить шероховатость поверхности после грубого шлифования примерно в 4 раза [8]. Вид профиля поверхности после тонкого шлифования показан на рис. 3.

Уравнение поверхности после тонкого шлифо-

G Yё = B 2 ( a n )( X - x 0 n - Х ё )² - 4 A ( a n ) x x [ C ( a n )( X - x 0 n - X ё )² - D ( a n )];

Y_ø – глубина канавок после тонкого шлифова-

ния;

^xn 1

^FX0 ⁺ G x0ui 2 C ( a n )

^{+ x} 0 n ^{+ x}ё ^;

^FX0 ^- G XXUI 2 C ( a n )

^{+ x} 0 n ^;

^FX0     B ^{( a} n ^{)( Y}0 ^y 0 n );

GX0 = B2 (an)(Y0 - У0n )2 - 4C(an) x x [ A (an)(Y0 - У0 n )2 - D (an)]-

В предложенной математической модели не учитывается шероховатость плоских участков поверхности между канавками, образуемая при тонком шлифовании алмазным диском.

вания имеет вид

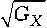
2 C ( a n )

⁺ x о n при

0 <  Y <  Y₀ ,    n = 1,2... N ;

2. Математическое моделирование формирования отверстий в керамических и ферритовых заготовках

X = i

'      ,  ^{+ x} 0 n ^{+ х}ё   ^п Р ^и

2 C ( a n )

Математическая модель профиля шерохова-

или

Y=

0 <  Y <  Y₀ ,    n = 1,2... N ;

X <  X 12 ,    X n 1 <  X <  x ( n + 1)2 ,   n = 1,2... N

при Y = Y 0 ;

xmin Y2n + x0 n < X < xmin Y2n + X0 n + Xё, n = 1,2... N при Y = 0

тости поверхности отверстия, полученного в заготовке трубчатым алмазным сверлом, разрабатывалась с использованием схемы образования стружки по Л.А. Глейзеру [8], согласно которой абразивными зернами на поверхности изделия наносится большое число рисок. Распределение

FY

-

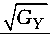
2 A ( a n )

+ y _{0 n}

при

x n 2 <  ^X <  ^x min Y 2 n ^{+ x} 0 n ,    ⁿ  1,2... ^N ;

^FYё ^- G YYji 2 A ( a n )

+ y _{0 n}

^x min Y 2 n ^{+ x} 0 n ^{+ Х}ё

при

< X <  x n 1 ,

n = 1,2... N ;

алмазных зерен по торцу и длине сверла принималось равномерным в соответствии с рис. 1. С учетом работы алмазных зерен, находящихся как на торцевой, так и на боковой поверхности сверла, профиль шероховатости поверхности полученного отверстия может быть аппроксимирован функцией [7]

r d = f ( z ) = - a sin

z 2 n

t

- a +   ,

Y₀  при  ( n = 1) X <  X 12   и

( n >  1)    x ( n - 1)1 <  X <  X n 2 ,    n = 1,2... N ;

0 при

^x min Y 2 n ^{+ x} 0 n <  ^X

< xmin Y2n + x0n + хё,   n = 1>2-N где

F Y = ^- B ^{( a} n ⁾⁽ X ^{- x} 0 n ^);

G Y = B ^{2 ( a} n ^{)( X - x} 0 n ^{) 2 - 4} A ^{( a} n ) ^x x [ C ( a n )( X - X 0 n ) 2 - D ( a n )];

F Yё =- B ( a n )( X - x 0 n - Х ё );

где r_d – уравнение поверхности отверстия; 2a – нормированная глубина рисок до шлифования; t – период следования рисок; d – нормированный диаметр отверстия; z – продольная координата.

Вид профиля поверхности отверстия после сверления алмазным сверлом схематически показан на рис. 4 штриховой линией.

При необходимости снижения глубины рисок в технологический маршрут включается этап тонкого шлифования поверхности отверстия заго- товки, осуществляемый ультразвуковым способом. Вид профиля поверхности отверстия после тонкого шлифования схематически показан на рис. 4 сплошной линией.

Математическая модель поверхности отверстия, с учетом (8), после тонкого шлифования может быть представлена в виде функции распределения рисок по его длине

. (z2п   п

- a sin      -

I t 2

d a +

при

rd

= f ( z ) =

I z <  z 0 d ⁺ nt ,

< [ z >  t - z о d + ( n - 1) t ;

d

- h + —

при

z > zo d + nt, z < t - z о d + nt, где n = 0,1...E(L /1), где rd – уравнение поверхности отверстия; 2a – нормированная глубина рисок до шлифования; t – период следования рисок; d – нормированный диаметр отверстия; h – нормированная глубина рисок после шлифования; L – длина отверстия; z – продольная координата;

t z0 d = 2П

. (h - a ) . п arcsin I I +

V a ) 2

– половина ширины риски после шлифования.

В предложенной математической модели не учитывается профиль шероховатости поверхности отверстия, образуемой при ультразвуковой обработке.

Заключение

На примере построения математических моделей основных этапов технологического процесса механической обработки керамических и ферритовых деталей показана возможность оптимизации процессов проектирования и изготовления керамических и ферритовых СВ× и КВ× функциональных узлов (с позиций получения наилучших технических характеристик при минимальных затратах на проектирование и технологическую подготовку производства). Аналогичные методы моделирования можно разрабатывать и применять для большинства основных формообразующих операций технологических процессов обработки элементов СВ×-и КВ×-устройств. Ýто позволит в существенной степени использовать скрытые резервы для улучшения характеристик создаваемых СВ× и КВ× функциональных узлов.

При построении аналогичных математических моделей для большинства основных операций механической обработки деталей СВ×- и КВ×-устройств, а также развитии представленных методов моделирования для других видов обработки, они могут быть введены в САПР СВ×-и КВ×-устройств. Ýто расширит возможности САПР и повысит качество проектирования этих устройств.