Математическое моделирование переходных процессов при селективном водозаборе из стратифицированного водоема
Автор: Музаев Илларион Давидович, Туаева Жанна Дмитриевна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.2, 2000 года.
Бесплатный доступ
Рассматриваются вопросы, связанные с математическим моделированием процесса селективного водозабора из стратифицированного водоема. Известно, что при расчете селективного водозабора определяют "критическое" положение поверхности раздела слоев, при котором не происходит захвата воды из загрязненных слоев водоема. Существующие расчетные формулы для определения "критического" положения поверхностей раздела слоев получены при условии установившихся (стационарных) движений воды в водоеме. Однако при включении и отключении водозаборного сооружения имеют место переходные (нестационарные) процессы, и на поверхности раздела образуются внутренние гравитационные волны, которые могут провоцировать нарушение селективного водозабора. В работе предложена новая математическая модель внутренних волн, генерированных вышеописанными переходными процессами.
Короткий адрес: https://sciup.org/14318008
IDR: 14318008 | УДК: 532(075.8)
Текст научной статьи Математическое моделирование переходных процессов при селективном водозаборе из стратифицированного водоема
Рассматриваются вопросы, связанные с математическим моделированием процесса селективного водозабора из стратифицированного водоема. Известно, что при расчете селективного водозабора определяют «критическое» положение поверхности раздела слоев, при котором не происходит захвата воды из загрязненных слоев водоема. Существующие расчетные формулы для определения «критического» положения поверхностей раздела слоев получены при условии установившихся (стационарных) движений воды в водоеме. Однако при включении и отключении водозаборного сооружения имеют место переходные (нестационарные) процессы, и па поверхности раздела образуются внутренние гравитационные волны, которые могут провоцировать нарушение селективного водозабора. В работе предложена новая математическая модель внутренних воли, генерированных вышеописанными переходными процессами.
В прямоугольной системе координат хОуг часть пространства, ограниченная условиями: 0 ^ х ^ L, О С У С В, —Но ^ о ^ Д, представляет стратифицированный водоем — источник водоснабжения. При этом — Но ^ о ^ 0 представляет нижний слой, а 0 < о < Hi — верхний слой с плотностями р0 и pi соответственно. Плоскость о = 0 — невозмущенная горизонтальная поверхность раздела, слоев, о = Hi — невозмущенная свободная поверхность верхнего слоя, о = — Яо — дно водоема.
Z м
Но р„
Рис. 1.
L
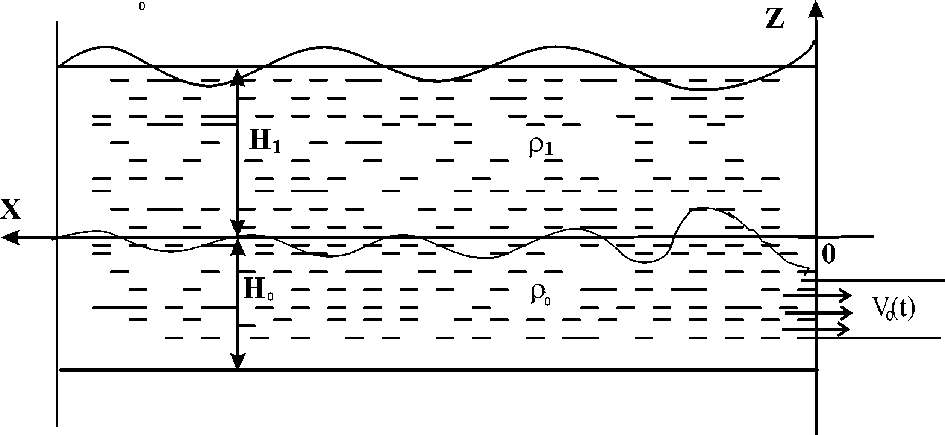
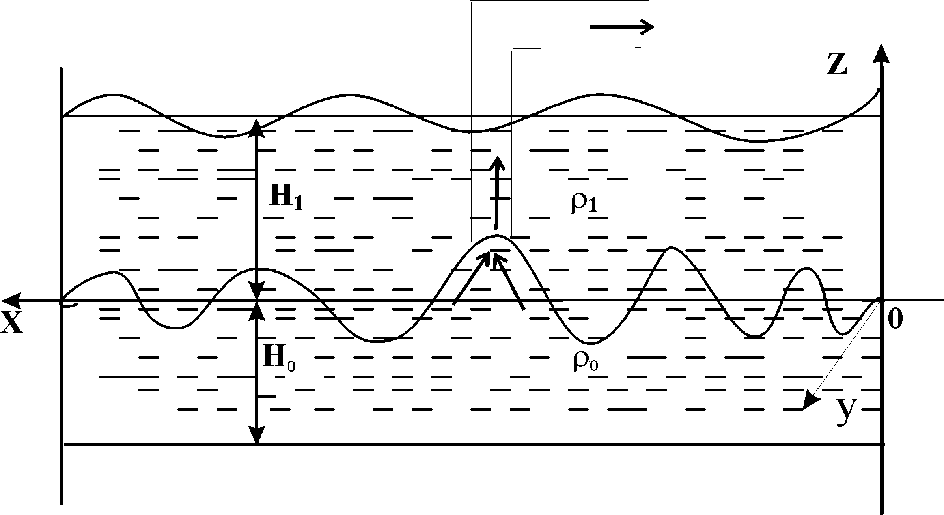
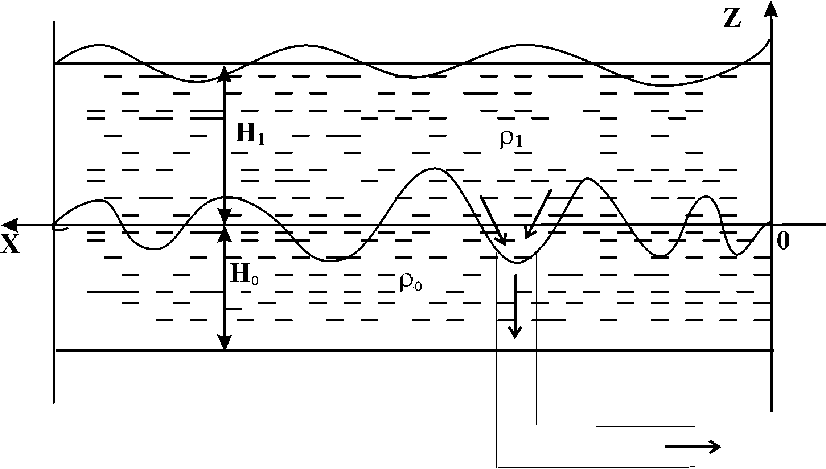
На участке напорной грани водоема ж = О, у0 - b < у < у0 + b, z0-a Потенциалы скоростей уд(ж, у, z, t) и уд (ж, у, z, t) в нижнем и верхнем слоях должны удовлетворять дифференциальным уравнениям Лапласа [2] д2Ро 5^0 5^0 Эх2 Эу2 dz2 -Но< г < 0, д2<Ц 5^i Э^уд Эх2 Эу2 dz2 0 < г < Н^ и следующим начальным и граничным условиям: Уро 9^1 п ^ = — = V1 = — = ° при t = 0, дуг Эх dvi Эх ж=0 5^0 Эх = 0, ж=0 5^0 Эх = 0, X—L VoW, z - z0+ ^ z ^ z - z0 - а, у - у0 + b ^ у ^ у - у0 - b, 0, в остальных случаях, 0, Эуо Эу = 0, У=о Эуо Эу = 0, В Эфу 9у = 0, У=0 Эфу Эу у=В = 0, (7) ( 92ф0 , ЭфД (92фу Эфуу Эфу Ри V 9t2 OZ / 2=0 pv у dt2 + 9-у— ) OZ / 5 ^ = 0 dz 9z , (8) 2 = 0 Эфо dz = о, - = -Я0 = О, 2 = Я! di2 где g — ускорение силы тяжести, (0, ?/о, ^о) — координаты центра водозаборного окна, 26 — ширина окна, 2а — высота окна. Рис. 2 При заборе воды из нижнего слоя в начально-краевой задаче (рис. 2) граничные условия (4) и (5) принимают вид Эфо VoW, z - z0 + a ^ z ^ z - z0 - а, у - у0 + b ^ у ^ у - у0 - b, -- = Эх 0 0, в остальных случаях, Эх = о, x=L Эфу Эх ж=0 Эфу Эх = 0. x=L При заборе воды по схеме, представленной на рис. 3, дифференциальное уравнение (1), начальные условия (3), граничные условия (4), (6)-(9) остаются неизмененными. Дифференциальное уравнение (2) и граничные условия (5) заменяются на следующие /(ж, -у, о) = [0(ж — ж0 + а) — 9^х — ж0 — а)] • Му - Уо + «) - 9(у - Уо - а)] • [фо - о0 + а) - 9^ - о0 - а)], где 9 — единичная функция Хевисайда. Легко заметить, что процесс водозабора из внутреннего пространства водоема смоделирован как непрерывная система точечных стоков равномерно распределенных в кубе Жо — а ^ ж ^ ж’о + а, уо — а ^ у ^ уо + a, oq — а ^ о ^ oq + а. При водозаборе из нижнего слоя по схеме (рис. 4) функция ^F^xpy,^ из дифференциального уравнения (2) перейдет в уравнение (1). Рис. 4 Поставленные начально-краевые задачи легко решаются методами операционного исчисления и конечных интегральных преобразований Фурье. Выражение для внутренней волновой поверхности r/(x,y,t) получено по схеме (рис. 1) для случая двумерной задачи в виде равномерно сходящегося тригонометрического ряда. Уравнение для уД^уД) выглядит следующим образом , м Pi Э^у Ро Эр>0 ЭДруД) =---—-----— при о = 0. Ро - pv at р0 - pv dt Потенциалы скоростей д0(ж,-У) и Д1(т,оу) находятся следующим образом. В результате применения интегрального преобразования Лапласа относительно времени t выражения (1)-(9) в изображениях для двумерного случая принимают следующий вид: Ро 9^1 Эх2 82фо Эх2 Э2фу -^ = 0, о^^Ях, Эх2 ЭД / 2 - , 9Фо = 0, -Но<0^0, (p2^i + = О, 2 = Я1 = Pi \р2Ф1 2 = 0 V Эфу Эх ^=0 ^1(ж, -Д yi(x, х, t^e ptdt, р Е С, Re р > 0. р)=/ p)=Z Й(ж, ~, где ф^^ = Jq фофс, х, р) cos(anx)dx, фЦ^ = /^ ф1(х, х,р) cos(anx)dx, an = nxjL. Решения дифференциальных уравнений (20) и (21) с граничными условиями (22)(24) имеют вид 1 Г ^(г) = C^ch(an^) + C^sh(an^) Ч--vi(s)sh(an(o - s^ds, (26) Р^тг Фп\^) ^п 1 / тг \ ’ sh(cin7io) где постоянные С^, С2 определяются из следующих равенств: -2 R. Р_ р2^1И(апЯ0)Яп сН(а„Я1) (1 + ^ЦапН^ЦапН0^ (р2 + ш^ Я1 ш1,п Э^п Я1 щ(8)сН(ап(Я1 — s^ds, ЩапН^ + 1Н(апЯ0) - л/Д г^ + ^н^я^н^Яо)) th(a^i) + th(anЯo) + л/Д? 9^п / \ ; 2М + ^Ца^Л^НоИ В результате выполнения обратного преобразования Лапласа и вычисления интегралов в последнем выражении оригинал выглядит следующим образом: Pi th(anЯo) dn = -уо^-щ-г" Rl,n(w2,„8111^2^ - wi,nsin(wiin£)) РО ^nW2,n ~ Ш1,п + Д2,п ---sm(win£)--sm(win£) \Ш1,П Wl,n/ где e-an(-o+a) _ е-а,1(2Я1-г0-а) _ e-a„(20-a) _ e-an(2Hi-^0+a) .TL 9 . ’ _|_ g 2a.n, H i Sn = 1 + —thanЯlth(anЯo). Po В результате выполнения обратного косинус-преобразования Фурье получается уравнение для поверхности раздела слоев при селективном водозаборе из двух- алойного стратифицированного водоема 0^,^ = -2^-d0 ^ P°L th(anЯo) SnH,n - Ш1,п) х ^1,п(ш2,п sin(w2,n£) - wi,n sin(wiin£)) + ^,Д — sin(o?ii„^ \Wi,n ----sin(w2in£) Ш2,п x cos(апж). Численные расчеты позволяют установить нижнее «критическое» положение раздела слоев и, тем самым, обеспечить селективный водозабор при переходных процессах в водозаборных сооружениях.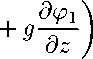
Эх2 ду2 Эх2
Qo(£) х
(10)
9^1
Эх
ж=0
о,
(11)
гДе QoW ~ расход воды через внутриводное
водозаборное отверстие, а
— некото-
рая фиктивная длина,
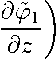
Эфо Эх
_ 8Фа_
2=0 9z
5
^ = 0
(16)
Эфо _
9z г=-н0”
о,
(17)
Эф1 1
9x хыГ Р
( х 9tPi п
-V1 о , —— = 0,
9Х x=L
(18)
Эх х—
_ Эфо, =0 9х Х-.
= 0, =L
(19)
Z
/ х 8^1
«о, -о -
а ^ х ^ Со + а,
«iR = —- = <
Эх
U х=0
0, о <
xq — а, х > xq + а,
~ ( \ Р1 ~
Ж^ЛЛ = , х РЖ
(ро - рлд
(ж, 0,7^) -
рфо(х, 0,79), (До - РЛ9
ipo^M^e ptdt,
Применим
в выражениях (12)-(19) конечное интегральное косинус-
преобразование Фурье относительно переменной х. Получим:
ффк-Дф^ЛЛ, о«г«Н1, (20)
Эх2 р
- «^< = 0, -Яо ^ ^ 0, (21)
(M + S^l) =0. (22)
/-«(M + g^l) =Р1(М + 9^1) , (23)
\ ) 2 = 0 V ' 2 = 0
Эф° Эф^ Эф®
=0, 24
92 2=0 92 2=0 9z г=-Щ
Pn^ = , х Р<(0) РФп^, (25)
\ро-рфд \ро-рфд
где
Р2 + (1 - ^ даДЦапН0)
Rn
сН(а„Я1) (1 + ^ЦапН^ЦапН0^ (р2 + ш^ (р2 + ш^
Список литературы Математическое моделирование переходных процессов при селективном водозаборе из стратифицированного водоема
- Большаков В. А. Справочник по гидравлике.-Киев: Вища школа, 1977.-280 с.
- Ламб Г. Гидродинамика.-М.: Изд-во технико-теоретической литературы, 1947.-928 с.
- Бочаров О. Б., Овчинников Т. Э. О проблемах моделирования течения идеальной стратифицированной жидкости в окрестности водозабора//Cб. научн. трудов "Вычислительные технологии", Новосибирск.-1993.-Т. 2, № 6.-C.163-167.


