Математическое моделирование показателей удовлетворенности потребителя и результативности СМК организации

Введение. Удовлетворенность потребителя — это ключевой показатель каждой компании, желающей повысить лояльность потребителей и тем самым улучшить характеристики своего бизнеса. Этот показатель является основой двух подходов к понятию качества [1]. Первый состоит в том, что качество определяется степенью расхождения между ожиданиями потребителей и их восприятием продукции. При такой точке зрения на качество считается, что если вы превзошли ожидания потребителей, то у вас хорошее качество. При втором подходе качество рассматривается как степень соответствия стандарту или спецификации. Но при этом упускается тот факт, что продукция может быть превосходно произведена, но в то же время может не удовлетворять нужды потребителя, более того, может не выдерживать конкуренцию на рынке среди аналогичных товаров.

Удовлетворенность — это чувство потребителя, которое он испытывает лишь после покупки и использования товара. При этом товар или марку компании воспринимают не изолированно, а в сравнении с реальной или воображаемой продукцией (услугами), которыми их можно заменить. Концепция ориентации на потребителей рассматривается как соответствие или превышение их ожиданий, а ожидания зависят от предлагаемого на рынке выбора. Превысив ожидания потребителей в цене и качестве, можно рассчитывать, что потребители останутся постоянными клиентами организации.

Постановка задачи. В соответствии с моделью Н. Кано (Noriaki Kano) [2], существует три уровня удовлетворенности (рис. 1).

Ожидаемое качество товара представляет собой совокупность параметров качества продукта, наличие которых потребитель считает обязательным (базовым). Существуют общепринятые стандарты обслуживания, которых придерживается большинство компаний в бизнесе. В противном случае клиенты могут отказываться от покупок, а при совершенствовании качества товара, удовлетворенность клиентов практически не увеличивается. Таким образом, существуют свойства товара, являющиеся необходимыми условиями удовлетворенности.

Желаемое качество товара принимается за основу при совершенствовании товара. Это направлено на возрастание удовлетворенности. Например, сокращение времени, которое клиенты проводят в очереди, вызывает пропорциональный рост удовлетворенности.

Привлекающее или волнующее качество товара представляет собой неожиданный по уровню сервис. При этом потребители бывают приятно удивлены. Например, получив в подарок шоколад, находясь в приемной какой-либо компании или стоя в очереди на регистрацию в гостинице. При этом надо иметь в виду, что такое волнующее качество вскоре превращается в ожидаемое. При определении удовлетворенности необходимо найти именно те показатели, которые наиболее полно раскрывают требования, желания и предпочтения потребителей. Таковыми могут быть показатели качества, которые характеризуют непосредственно объект, его свойства.

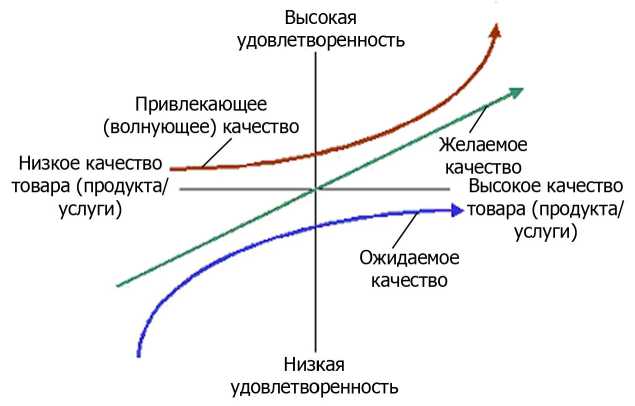
Рис. 1. Три уровня удовлетворенности по Н. Кано

Методы решения задачи. Данные об удовлетворенности потребителя товарами или услугами можно получить двумя основными способами: при проведении опроса по специально разработанным анкетам, либо косвенно — на основании собственных данных о взаимоотношениях с клиентами. При опросе потребителя можно пользоваться различными методами: рассылкой анкет по электронной почте, факсу, интервьюированием лично или по телефону. Косвенными признаками удовлетворенности клиента являются объем продаж продукции, длительность деловых связей с клиентами, процент постоянных клиентов, процент потерянных клиентов и т. д. Следует учитывать, что отдельно взятый показатель может не иметь особого значения для клиента, а группа показателей, в которую он входит, имеет большое значение. Для более точного определения тех показателей, которым отдается предпочтение, используется метод экспертных оценок, основанный на использовании обобщенного опыта и интуиции компетентных специалистов — экспертов. По присвоенным экспертами рангам показателей определяются веса. При этом самый важный показатель имеет самый большой вес. Экспертный метод применен для ранжирования показателей качества работ строительной организации и медицинского учреждения.

Экспертным анализом был выявлен 41 показатель ремонтно-строительного предприятия. Показатели разделены на 11 групп. Всем группам показателей на основании мнений экспертов присвоены веса в зависимости от их значимости. Распределение весомости групп представлено на рис. 2. Затем проведено расслоение групп по отдельно взятым показателям и распределение весов внутри групп для группы «Потребительские показатели» (рис. 3).

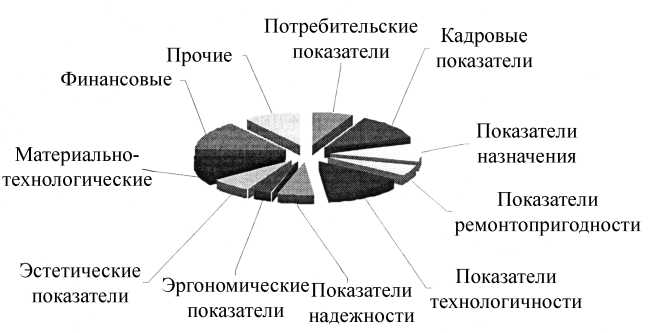
Показатели назначения

Показатели ремонтопригодности

Материальнотехнологические

Эстетические /       /         \      \ Ппкяяятрпи

Эргономиче ские Показатели    11оказатели показатели Р я^трпы показатели технологичности показатели надежности

Потребительские Кадровые

Прочие л показатели / показатели Финансовые л \             /

Рис. 2. Распределение весов по группам показателей

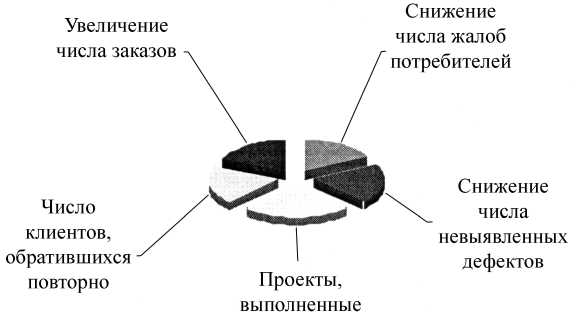
в срок

Рис. 3. Расслоение группы «Потребительские показатели» (в процентах)

Удовлетворенность потребителя тесно связана с другими критериями результатов и зависит от различных процессов и возможностей. Таким образом, удовлетворенность потребителя — это интегральная часть структуры, построенной на причинно-следственных связях. Надежное и эффективное измерение и прогнозирование удовлетворенности потребителя должно отражать это положение, т. е. должно быть основано на структурной модели (рис. 4).

Требования обоснованности и работоспособности подразумевают наличие структурных моделей совокупного качества продукции, основанных на скрытых факторах, где каждый такой фактор представлен рядом измеряемых явных переменных. Латентные факторы структурно связаны внутренними соотношениями, и каждый фактор определен явными переменными согласно зависимостям внешних измерений [3]. Статистическая оценка таких моделей усложнена, поскольку и внутренние и внешние соотношения имеют существенную мультиколлинеарность. Непосредственно измеренные данные не всегда могут раскрыть всю ситуацию. Для наиболее полного ее понимания используются различные способы оценки, такие, как метод частичных наименьших квадратов, метод максимального правдоподобия, подходы нейронных сетей [4].

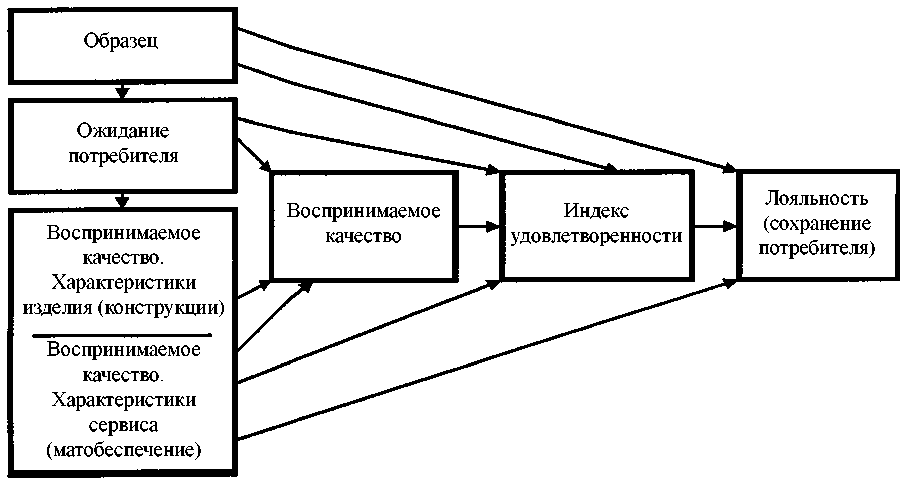
Рис. 4. Структурная модель для измерения удовлетворенности потребителя

Измерение удовлетворенности потребителя должно быть основано на структурной модели. Внимание организации сосредоточено на оперативных решениях, приоритетных в отношении качества, при большом числе стимулирующих возможностей, что подразумевает много факторов и явных переменных. Полученные результаты должны использоваться не только для оценки текущего уровня удовлетворенности, а следовательно, и качества продукции, но и для прогнозирования спроса и потребностей. Для этого необходимо создать математическую модель показателей качества. В результате математического моделирования определяют исходные ранговые функции для показателей качества и реорганизуют на их основе группы критериев. Методика математического моделирования. При использовании исходного соотношения весов показателей качества в пределах групп получается ранговый портрет системы оценивания удовлетворенности потребителя, например при производстве строительных работ. В первую очередь определяется ранговый вес каждой группы в целом и индексный вес каждого отдельного критерия. При этом учитываются веса критериев, не отнесенных ни к одной из групп. Соотношения ранговых весов для групп, полученные в результате анализа, представлены в табл. 1.

Таблица 1

Исходное распределение ранговых весов по группам

Наименование группы показателей	Число показателей	Ранговы й вес I	Относительный весовой коэффициент W
Показатели назначения	2	53	0,0616
надежности	2	37	0,0430
ремонтопригоднос ти	2	15	0,0174
технологичности	4	70	0,814
Эргономические показатели	5	80	0,0930
Эстетические	3	115	0,01337
Экономические	10	203	0,02360
Прочие показатели	15	287	0,3337
Итого :	43	860	1

При определении ранговых функций использованы три аппроксимирующие функции: линейная, экспоненциальная, гиперболическая [5].

При использовании линейной функции были включены следующие параметры:

W = a i N + C i ,                                     (1)

где W — относительный ранговый вес; a i и С i — внутренние параметры аппроксимирующей функции; i — номер группы; N — номер рангового веса группы (или показателя в пределах группы).

При использовании экспоненциальной функции были включены следующие параметры:

W = e ^ai^{N +} b i + C i .                                          (2)

При использовании гиперболической функции были включены следующие параметры:

W =

ai biN + di + k

+ C i ,

где b i , d i — внутренние параметры аппроксимирующей функции; k — фиксированная постоянная (обеспечивает корректность области допустимых значений для гиперболы).

При наличии в группе двух критериев использована линейная функция распределения. При большем количестве ранговых компонентов (критериев) использовались экспоненциальная и гиперболическая аппроксимация. Для проверки на адекватность аппроксимирующей функции использован дисперсионный критерий R . При расчетах заложена возможность ошибки 5 % ( ± 2,5 %). Аппроксимация выполнена с помощью табличного процессора Microsoft Excel с использованием модуля «Поиск решения» [6].

Результаты математического моделирования. В результате для групп получена следующая ранговая функция:

W =

0,1088

- 0,1845 N + 2,3272

- 0,0553.

Результаты аппроксимации ранговой функции по группам представлены в табл. 2 и на рис. 5.

Таблица 2

Результаты аппроксимации ранговой функции по группам

Наименование группы показателей	Рангов ый вес I	Относительный весовой коэффициент W
		исходный	рассчитанный
Показатели назначения	53	0,0616	0,0178
надежности	37	0,0430	0,0419
ремонтоприго дности	15	0,0174	0,0282
технологичнос ти	70	0,814	0,0611
Эргономические показатели	80	0,0930	0,0898
Эстетические	115	0,01337	0,1370
Экономические	203	0,02360	0,2301
Прочие показатели	287	0,3337	0,4976

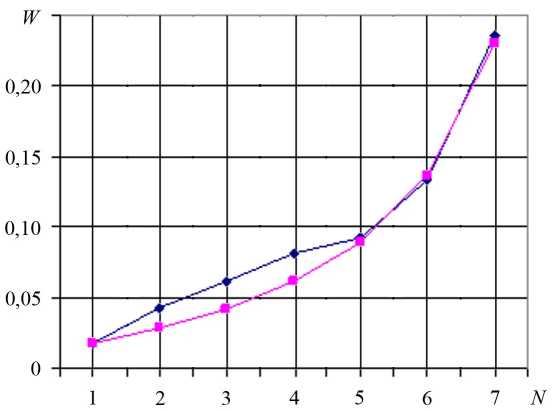
Рис. 5. Распределение весов по группам:

- ♦ - — исходные веса; - ■ - — аппроксимация

Выводы. Установлено, что закон распределения весовых коэффициентов для критериев групп соответствует гиперболическому закону. Это дает возможность дополнять группы и вычислять ранговые веса новых групп. При дополнении ранговый закон не изменяется. Данный способ можно использовать для анализа каждой группы. При внутригрупповом анализе можно проверить ранговый закон для группы и применить его при реорганизации внутри группы, т. е. при добавлении и удалении критериев. При делении групп закон распределения весов можно принять для искомой группы или воспользоваться межгрупповым законом.

Данный метод может быть использован при планировании многокритериальных систем менеджмента качества на предприятиях.